В каком классе изучают свойство гипотенузы прямоугольного треугольника
Сахаров Алексей Павлович, учитель математики,
Частное общеобразовательное учреждение «Школа – интернат №3
среднего общего образования ОАО «РЖД» г. Ртищево Саратовской области
Конспект урока геометрии в 8 классе по теме: «Теорема Пифагора»
Тема урока: «Теорема Пифагора».
Цель урока: Дать понятие о теореме Пифагора, о многообразии способов ее доказательства, первичное применение теоремы для решения задач.
Задачи урока:
исследовать закономерности между сторонами прямоугольного треугольника; изучить теорему Пифагора; формировать умения применять теорему Пифагора при решении задач;
УУД:
Познавательные: развивать основы логического и алгоритмического мышления; расширять кругозор учащихся; развивать интерес к математике.
Регулятивные: развивать умения читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;
Коммуникативные: строить высказывания, аргументировано доказывать свою точку зрения;
Личностные: развивать навыки сотрудничества со сверстниками, внимания, памяти, воображения.
Тип урока:формирование новых знаний и умений.
Формы работы учащихся:фронтальная, индивидуальная, групповая.
Необходимое техническое оборудование:компьютер, проектор.
Дидактические средства: учебник, электронная презентация, раздаточный материал.
Методы и приемы: фронтальная работа, сочетающаяся с общеклассной; частично-поисковый метод; индивидуальная работа; работа в парах.
Эпиграф урока:“Геометрия владеет двумя сокровищами, одно из них – …”. (слайд 1)
Иоганн Кеплер
План урока:
Организационный момент. (1 мин.)
Устная работа. (10 мин.)
Проблемная ситуация. (5 мин.)
Сообщение главной цели урока.
Исследовательская работа (в парах).
Изучение нового материала. (10 мин.)
Физминутка.
Закрепление изученного материала. ( решение задач) (10 мин.)
Применение теоремы Пифагора.
Подведение итога урока. (1 мин.)
Домашнее задание. (3 мин.)
Рефлексия.
Ход урока.
Организационный момент.
Устная работа.
Какая геометрическая фигура изображена на экране? (слайд 2).
Какой треугольник называется прямоугольным?
Сторона прямоугольного треугольника, лежащая против прямого угла,называется… (слайд 3).
Стороны, образующие прямой угол, называются…
Учитель. Сформулируйте свойства прямоугольных треугольников, которые мы уже знаем (слайд 4).
Продолжите предложения:
Сумма двух острых угловпрямоугольного треугольника равна . (слайд 5).
По рисунку найдите угол 3 если сумма углов 1 и 2 равна 900. (слайд 6).
Катет прямоугольного треугольника, лежащий против угла в , равен половине гипотенузы. (слайд 7).
– Один из углов прямоугольного треугольника равен 15°. Чему равны остальные углы?
– Один из углов из углов прямоугольного треугольника равен 30°, катет, противолежащий ему, равен 13 см. Чему равна гипотенуза?
– Катет прямоугольного треугольника равен 16 дм, гипотенуза – 32 дм. Найдите углы треугольника.
Учитель. – Сформулируйте признаки равенства прямоугольных треугольников
Сначала учащиеся формулируют признаки равенства прямоугольных треугольников, а затем переходим к решению задач на доказательство по готовым чертежам:
Докажите, что треугольники равны. (слайд 8).
Учитель. Посмотрим, что вы помните о свойствах площадей: (слайд 8).
– Равные многоугольники имеют … (слайд 9).
– Если многоугольник составлен из нескольких многоугольников, то его площадь равна … (слайд ).
– Площадь квадрата равна … (слайд 10).
– Сторона квадрата 14 см. Чему равна площадь квадрата?
– Площадь квадрата 225 м2. Найдите его сторону.
– Площадь прямоугольного треугольника равна … (слайд 11).
– Катеты прямоугольного треугольника 4 см и 8 см. Найдите его площадь.
Проблемная ситуация.
А теперь давайте решим небольшую задачу. (слайд 12)
Задача 1. Велосипедист и пешеход отправились одновременно из одного населенного пункта в противоположных направлениях. Пешеход пошел на запад со скоростью 5 км/ч, а велосипедист поехал на восток со скоростью 12 км/ч. Какое расстояние будет между ними через час?
На каком предмете обычно решают такие задачи?
Задача 2. Велосипедист и пешеход отправились одновременно из одного населенного пункта в разных направлениях. Пешеход пошел на юг со скоростью 5 км/ч, а велосипедист поехал на восток со скоростью 12 км/ч. Какое расстояние будет между ними через час? (слайд 13)
Какая фигура получилась? Какие стороны известны? Что найти?
Тех знаний о прямоугольном треугольнике, которые мы имеем, не хватает. Последнюю задачу решить не можем.
Сформулируйте то, что мы должны знать, чтоб решить эту задачу? Это и будет целью нашего урока.
Сообщение главной цели урока.
Цель нашего урока как раз и заключается в том, чтобы выяснить, как связаны между собой стороны прямоугольного треугольника. (слайд 14)
Исследовательская работа (в парах).
Чтоб это выяснить, мы займемся исследовательской деятельностью. Работаем в парах.
1) Учащиеся, получившие бумажные треугольники, выполняют задание:
а)Измерьте стороны треугольников и заполните таблицу на доске:
№
a
b
c
a 2
b 2
c 2
a 2 + b 2
1.
8
15
17
64
225
289
289
2.
7
24
25
49
576
625
625
3.
6
8
10
36
64
100
100
2) (дополнительное) Я вам раздам лист, на котором оранжевым цветом закрашен равнобедренный прямоугольный треугольник, на сторонах которого построены квадраты. Ответьте на два вопроса и сделайте вывод.
Вывод: Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Так изначально формулировалась теорема Пифагора.
Вычислите, чему равен квадрат гипотенузы.
Найдите сумму квадратов катетов.
Какой можно сделать вывод?
Ученик. Квадрат гипотенузы равен сумме квадратов катетов.
Можно ли из данных этой работы сделать такой вывод о связи катетов и гипотенузы всех прямоугольных треугольников? (Нет, т. к. из частных случаев не следуют общие заключения).
Учитель.
То, к чему мы пришли опытным путем, доказал древнегреческий ученый Пифагор в 6 в. до н. э. Он не открыл эту теорему (она была известна еще в Древнем Египте и Вавилоне), а нашел ее доказательство.
Итак, какова же тема нашего сегодняшнего урока? ( «Теорема Пифагора»). (слайд 15)
Эта теорема является основой решения множества геометрических задач и базой изучения теоретического материала в дальнейшем. Сама же теорема Пифагора замечательна тем, что она проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное практическое значение: она применяется в геометрии буквально на каждом шагу.
Докажем эту теорему и решим несколько задач с её применением.
Вероятно, факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников (слайд 16).
Предполагают, что во времена Пифагора теорема звучала так:
“Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах”.
Действительно, с2 – площадь квадрата, построенного на гипотенузе, а2 и b2 – площади квадратов, построенных на катетах.
Квадрат, построенный на гипотенузе, содержит четыре треугольника. А на каждом катете построен квадрат, содержащий два треугольника. На рисунке вы видите, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.
В древние времена, доказывая эту теорему, чертили чертёж и просто говорили: «Смотри!».
Возникает вопрос, для любого ли прямоугольно треугольника справедливо это равенство или только для равнобедренного прямоугольного треугольника?
Изучение нового материала.
«Для того чтобы усовершенствовать ум, надо больше рассуждать, чем заучивать».
Р. Декарт
Учитель.
– А кто из вас что-нибудь слышал об этой теореме? (Пифагоровы штаны на все стороны равны).
– Действительно, это шуточная формулировка теоремы. Почему так говорят, вы узнаете несколько позже, сейчас докажем теорему Пифагора в современной формулировке. Я хочу, чтобы вы попробовали доказать её сами, используя свойства площадей и метод, который мы использовали при введении формул сокращённого умножения, при выводе формул площадей некоторых фигур.
Теорема:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Выделите в данной теореме условие и заключение.
Ученик. Условие: в прямоугольном треугольнике. Заключение: квадрат гипотенузы равен сумме квадратов катетов.
Итак, нам дан прямоугольный треугольник с катетами a, b, гипотенузой с.
а
в
Запись на доске:
А
с
с
а
в
Дано:
с
в
∆АВС;
с
С=90;
с
а
а
в
С
В
АВ=с;
ВС=а;
а
в
АС=в;
Док-ть:
Учитель. Доказательство:
Достроим прямоугольный треугольник c катетами a, b, гипотенузой с до квадрата со стороной a+b. (Далее доказательство сопровождается пошаговой иллюстрацией производимых действий).
Площадь S этого квадрата равна
С другой стороны, этот квадрат составлен из четырех равных прямоугольных треугольников, площадь каждого из которых равна, и квадрата со стороной , поэтому
Таким образом,
Теорема доказана.
Найдите формулировку теоремы в учебнике.
Физминутка.
Устали? Чтоб немного отдохнуть от умственной деятельности, давайте разомнемся!
Минута отдыха. Стихотворение, посвящённое теореме.
Если дан нам треугольник,
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путём
К результату мы придём.
Закрепление изученного материала (решение задач).
Мы доказали с вами одну из важнейших теорем геометрии. Давайте попробуем решить с её помощью несколько задач по готовым чертежам устно (слайд 17).
Все задачи можно разделить на два типа
Задача 1
Замечание: Из курса алгебры известно, что уравнение АВ= 100 имеет два корня АВ = +. АВ = -10 не удовлетворяет условию задачи, так как длина стороны треугольника всегда положительна. Значит АВ = 10. В дальнейшем при решении уравнений в подобных задачах, мы будем находить только положительные корни, и не будем объяснять каждый раз почему отрицательные корни отбрасываются.
Задача №2
Мы с вами получили треугольник со сторонами 3, 4 и 5 единиц. Это единственный прямоугольный треугольник, стороны которого равны трём последовательным натуральным числам. Его часто называют египетским треугольником, так как он был известен ещё древним египтянам. Они использовали этот треугольник в «правиле верёвки» для построения прямых углов при закладке зданий, храмов, алтарей и т.п. Об этом мы поговорим подробнее на следующем уроке.
Вернёмся теперь к задаче про велосипедиста и пешехода, которую мы не смогли решить в начале урока. (слайд 18).
Теперь мы легко можем найти расстояние, которое будет между велосипедистом и пешеходом через 1 час.
Рассмотрим ещё две задачи не из школьного учебника.
Решение задачи индийского математика XII века Бхаскары (слайды 19 – 20)
и из учебника Леонтия Магницкого. (слайд 21).
Применение теоремы Пифагора.
Значение теоремы Пифагора состоит в том, что из нее или с ее помощью можно вывести множество теорем геометрии и решить много задач. (слайд 22)
ВИДЕО
Видеоролик мультяшной формы из интернета (1,5 мин.) (переход по гиперссылке к слайду 25).
Подведение итогов.
Итак, сегодня на уроке мы познакомились с одной из главных теорем геометрии – теоремой Пифагора и её доказательством, с некоторыми сведениями из жизни учёного, имя которого она носит, решили несколько простейших задач.
Теорема Пифагора замечательна и тем, что сама по себе она вовсе не очевидна, не смотря на внешнюю простоту.
Например, свойства равнобедренного треугольника можно видеть непосредственно на чертеже.
Но сколько ни смотри на прямоугольный треугольник, никак не увидишь, что между его сторонами есть простое соотношение: c2 = a2 + b2.
Кто уже запомнил формулировку теоремы Пифагора?
Пригодятся вам эти знания?
Популярность теоремы настолько велика, что доказательств очень-очень много. В некоторой литературе указывается, что их более 500. Может, вы сами захотите найти другие доказательства, больше узнать о Пифагоре. На следующем уроке мы рассмотрим некоторые из них.
Домашнее задание (слайд 23).
п. 54. № 483, 484
Почему теорему Пифагора называли «Теоремой невесты»?
Найти какое-нибудь доказательство, отличное от рассмотренных на уроке (по желанию).
Рефлексия
Понравился вам урок?
Памятник Пифагору находится в порту города Пифагория на острове Самос и напоминает всем о теореме Пифагора, наиболее известном его открытии. Катет, лежащий в основании треугольника – мраморный, гипотенуза и фигура самого Пифагора в виде второго катета – медные. (слайд 24).
СПАСИБО ЗА УРОК!
Источник
Цели:
Образовательные:
- Исследовать и доказать свойства прямоугольного треугольника.
- Формировать умения и навыки применять их к решению задач.
Развивающие:
- Развивать познавательную активность, творческие способности и интерес к предмету.
- Развивать логическое мышление, умение сравнивать, анализировать, обобщать, решать проблемные ситуации, делать выводы.
Воспитательные:
- Учить прислушиваться к мнению своих товарищей.
- Развивать умения работать в группах.
Оборудование: Компьютерный класс, презентация, карточки с готовыми чертежами, презентация, контрольный тест в виде презентации на два варианта, карточки с заданиями теста (если нет компьютерного класса).
Тип занятия: урок доказательства теоремы.
Ход урока
1. Подготовительный этап (Актуализация знаний)
Цель: повторить теорему о сумме углов треугольника, определение и свойства внешнего угла треугольника, виды треугольников по углам и по сторонам, элементы прямоугольного треугольника
– Какие темы мы изучали на последних уроках? (сумма углов треугольника, неравенство треугольника, внешний угол треугольника)
– Какая фигура называется треугольником?
– По каким элементам мы классифицировали треугольников? (по сторонам, по углам)
– Какие существуют виды треугольников по сторонам? (разносторонние, равнобедренные, равносторонние)
– На какие виды делятся треугольники по углам? (остроугольные, тупоугольные, прямоугольные)
Учитель фиксирует на доске названные виды треугольников в два столбика с помощью табличек и магнитов.
– Свойства каких из перечисленных треугольников мы уже изучали? (остроугольных, равнобедренных, равносторонних)
Учитель фиксирует на доске названные виды с помощью магнитов другого цвета.
– О свойствах каких треугольников мы знаем меньше всего? (прямоугольных)
– Как вы думаете, что мы сегодня будем изучать на уроке?
Сформулируйте тему нашего сегодняшнего урока. (Свойства прямоугольных треугольников)
Можем ли мы на одном уроке изучить все свойства прямоугольных треугольников? (Нет)
Значит тема ……. Некоторые …..
– Молодцы. Откройте тетради. Запишите дату и тему урока.
– Какие перед нами стоят цели?
(выявить свойства прямоугольных треугольников, доказать их, научиться применять их на практике при решении задач).
УСТНО:
1) Какой треугольник называется прямоугольным?
2) Как называются стороны прямоугольного треугольника?
3) Что такое гипотенуза и катеты?
2. Мотивационный этап
Цель: Побуждение интереса к изучению теоремы об угле 30 градусов в прямоугольном треугольнике, подведение обучающихся к раскрытию содержания теоремы. Прием – лабораторная работа.
Учащиеся разделены на 5 групп. Группы получают карточки с готовыми чертежами и соответствующими вопросами на выбор для исследования.
Вопрос №1: Чему равна сумма двух острых углов в прямоугольном треугольнике?
Вопрос №2: Какая взаимосвязь между сторонами прямоугольного треугольника, у которого один из острых углов равен 30 градусов?
Вопрос №3: Какая особенность у прямоугольных треугольников, в которых один из катетов равен половине гипотенузы?
Задание для исследования 1 группе
По рисунку найдите неизвестные углы, заполните таблицу.
№ | Углы | ||||
С | А | В | А + В | ||
1 | 30⁰ | → | |||
2 | 50⁰ | → | |||
3 | 25⁰ | → | |||
4 | 45⁰ | → | |||
Сделайте вывод о сумме острых углов прямоугольного треугольника.
Сумма острых углов прямоугольного треугольника ________________
Задание для исследования 2 группе
Измерьте катет напротив угла в 30⁰ и гипотенузу, заполните таблицу.
№ | С | А | ВС | АВ |
1 | ||||
2 |
Сделайте вывод: Какая взаимосвязь между сторонами прямоугольного треугольника, у которого один из острых углов 30⁰?
В прямоугольном треугольнике напротив угла в 300 лежит ______________________
Задание для исследования 3 группе
Измерьте угол против катета, который в 2 раза меньше гипотенузы. Заполните таблицу.
№ | С | ВС (мм) | АВ (мм) | Ð А |
1 | → | |||
2 | → |
Сделайте вывод: Какая особенность у острого угла прямоугольного треугольника, в котором один из катетов равен половине гипотенузы?
В прямоугольном треугольнике против катета равного половине гипотенузы лежит _______________________________
После того, как учащиеся приходят к какому-то выводу, представитель каждой группы выдвигает свою гипотезу.
Предполагаемые гипотезы:
1. Сумма двух острых углов прямоугольного треугольника равна 900.
2. Катет прямоугольного треугольника, лежащий против угла в 300,
равен половине гипотенузы.
3. Если катет прямоугольного треугольника равен половине гипотенузы,
то угол, лежащий против этого катета, равен 300.
– ВНИМАНИЕ, ребята!!!
Гипотеза – это всего лишь предположение, которое просто необходимо доказать!
На доске (заранее на обратной стороне) чертежи свойств с «дано» и «доказать».
3. Ориентировочный этап
Цель: ввести формулировки теорем и организовать работу по усвоению теорем о свойствах прямоугольного треугольника.
Метод – частично-поисковый.
Теорема: Катет, лежащий против угла 30 градусов, равен половине гипотенузы.

Дано:
∆ ABC,
∠C=90º,
∠A=30º.
Доказать:
BC = ½ AB
Доказательство:
I способ
Так как сумма острых углов прямоугольного треугольника равна 90º, то
∠B = 90º – ∠A=90º – 30º = 60º.
Проведем из вершины прямого угла медиану CF.
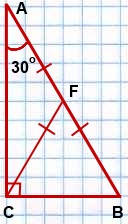
Так как медиана, проведенная к гипотенузе, равна половине гипотенузы, то CF = ½AB,
то есть, CF = AF = BF.
Так как BF=CF, то треугольник BFC — равнобедренный с основанием BC.
Следовательно, у него углы при основании равны:
∠B=∠BCF=60º.
Так как сумма углов треугольника равна 180º, то в треугольнике BFC
∠BFC =180º – (∠B+∠BCF) = 60º.
Поскольку все углы треугольника BFC равны, то этот треугольник — равносторонний.
Значит, все его стороны равны и BC = CF = BF = ½ AB.
Что и требовалось доказать.
II способ
Так как сумма острых углов прямоугольного треугольника равна 90º, то
∠B=90º–∠A=90º–30º=60º.
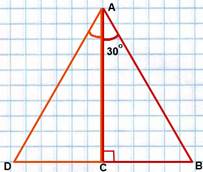
Построим треугольник ADC, равный треугольнику ABC.
В нем ∠D=∠B=60º и ∠CAD=∠CAB=30º (по построению).
Отсюда, ∠BAD=∠CAD+∠CAB=60º.
Следовательно, в треугольнике ABD все углы равны:
∠BAD =∠D =∠B = 60º.
Значит, треугольник ABC — равносторонний, и все его стороны равны: AB=AD=BD.
BC=DC (по построению), поэтому BC = ½ BD = ½ AB.
Что и требовалось доказать.
Попробуйте доказать теорему любым их двух способов.
Катет __________________________ треугольника, лежащий против угла в ____0, равен ______________________ гипотенузы.
Дано:
Δ АВС
∠С = 90º
∠В = 30º
Доказать: АС = ½ АВ
Доказательство:
4. Первичное применение теоремы
После доказательства свойствпрямоугольного треугольника учащимся предлагаются задачи на готовых чертежах (слайды). Задачи решаются устно, быстро.

Один ученик у доски, остальные в тетради.
Задача № 257, стр. 81 (если позволит время).
Дано:
ΔАВС.
∠ С = 90⁰,
∠ ВАD = 120⁰,
AС + АВ = 18 см
Найти: АС, АВ.
Решение: ∠ВАD = 120⁰ = > ∠В = 30⁰
АС = ½ АВ (по свойству катета, лежащего против угла в 30⁰)
Если АС = х см, то АВ = 2х см, тогда, учитывая условие, х + 2х = 18, х = 6, т.е. АС = 6 см, АВ = 12 см
5. Тест с взаимопроверкой в парах и самооценкой (см. приложения)
Ответы записывают на листочках. Затем проверяют по образцу с помощью компьютера (работа в парах) и сами ставят себе оценку.
Критерии:
- «3» – четыре верных ответа.
- «4» – пять верных ответов.
- «5» – шесть-семь верных ответов.
6. Подведение итогов. Домашнее задание (слайд презентации).
Выбрать задание одного из уровней:
Провести доказательство гипотезы 2 и 3 дома самостоятельно и внести их на шаблоны.
В _______________________ треугольнике сумма ____________
равна ____________ .
Дано:
Δ АВС
∠С = 90⁰
Доказать: ∠А + ∠В = 90⁰
Доказательство:
Если катет _____________ треугольника равен ___________ гипотенузы, то угол лежащий против этого катета, равен _____.
Дано:
Δ АВС
∠С = 90⁰
АС = ½ АВ
Доказать: ∠В = 30⁰
Доказательство:
- Пункт 34: выучить все свойства и доказательство любых двух. № 255.
- Пункт 34: выучить все свойства и их доказательство. № 258
- Пункт 34: выучить все свойства и их доказательство. № 260
Творческое задание (по желанию): придумать и решить задачу на применение всех трех свойств прямоугольного треугольника.
8. Рефлексия.
До сегодняшнего дня мы не знали свойств прямоугольных треугольников, а сегодня вы сами исследовали их, выдвинули гипотезу и доказали.
Оцените насколько хорошо вы справились с поставленной задачей
Как вы оцените свою работу на уроке, к какому уровню себя отнесете? (презентация):
- Я всё понял и могу доказать все свойства.
- Я всё понял и могу доказать некоторые свойства.
- Для полного понимания мне необходимо повторить тему дома.
- Я ничего не понял.
Источник
