В какой треугольник можно вписать окружность свойства

Серединный перпендикуляр к отрезку
Определение 1. Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).

Рис.1
Теорема 1. Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство. Рассмотрим произвольную точку D, лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.

Рис.2
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB. Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1). Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство. Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D.

Рис.3
Докажем, что отрезок AE длиннее отрезка EB. Действительно,
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.

Рис.4
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE. Действительно,
Полученное противоречие и завершает доказательство теоремы 2
Окружность, описанная около треугольника
Определение 2. Окружностью, описанной около треугольника, называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником.

Рис.5
Свойства описанной около треугольника окружности. Теорема синусов
| Фигура | Рисунок | Свойство |
| Серединные перпендикуляры к сторонам треугольника |  | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство |
| Окружность, описанная около треугольника |  | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности |  | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |  | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |  | Для любого треугольника справедливы равенства (теорема синусов): , где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Площадь треугольника |  | Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Радиус описанной окружности |  | Для любого треугольника справедливо равенство: где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Серединные перпендикуляры к сторонам треугольника |
 Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство |
| Окружность, описанная около треугольника |
 Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности |
 Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. |
| Центр описанной около прямоугольного треугольника окружности |
 Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |
 Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |
 Для любого треугольника справедливы равенства (теорема синусов): , где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Площадь треугольника |
 Для любого треугольника справедливо равенство: S = 2R2 sin A sin B sin C , где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
| Радиус описанной окружности |
 Для любого треугольника справедливо равенство: где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности. Посмотреть доказательство |
Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3. Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство. Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC, и обозначим точку их пересечения буквой O (рис. 6).

Рис.6
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC, то в силу теоремы 1 справедливо равенство:
CO = AO .
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB, то в силу теоремы 1 справедливо равенство:
AO = BO .
Следовательно, справедливо равенство:
CO = BO ,
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие. Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство. Рассмотрим точку O, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
AO = OB = OC ,
из которого вытекает, что окружность с центром в точке O и радиусами OA, OB, OC проходит через все три вершины треугольника ABC, что и требовалось доказать.
Теорема 4 (теорема синусов). Для любого треугольника (рис. 7)

Рис.7
справедливы равенства:
.
Доказательство. Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R, на которую опирается вписанный угол величины φ , вычисляется по формуле:
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).

Рис.8
Угол MPN, как угол,опирающийся на диаметр, является прямым угломугол,опирающийся на диаметр, является прямым углом, и равенство (1) вытекает из определения синуса угла прямоугольного треугольника.
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
Теорема синусов доказана.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник
Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Напомним определение биссектрисы угла.
Определение 1. Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла). Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).

Рис. 1
Доказательство. Рассмотрим произвольную точку D, лежащую на биссектрисе угла BAC, и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE, а гипотенуза AD – общая. Следовательно,
DF = DE,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1). Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).

Рис. 2
Доказательство. Рассмотрим произвольную точку D, лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE, а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2. Окружность называют окружностью, вписанной в угол, если она касается касается сторон этого угла.
Теорема 3. Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство. Пусть точка D – центр окружности, вписанной в угол BAC, а точки E и F – точки касания окружности со сторонами угла (рис.3).

Рис.3
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности), а гипотенуза AD – общая. Следовательно
AF = AE,
что и требовалось доказать.
Замечание. Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных, проведенных к окружности из одной точки, равны.
Напомним определение биссектрисы треугольника.
Определение 3. Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4. В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство. Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC, и обозначим точку их пересечения буквой O (рис. 4).

Рис. 4
Опустим из точки O перпендикуляры OD, OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC, то в силу теоремы 1 справедливо равенство:
OD = OE,
Поскольку точка O лежит на биссектрисе угла ACB, то в силу теоремы 1 справедливо равенство:
OD = OF,
Следовательно, справедливо равенство:
OE = OF,
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC. Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4. Окружностью, вписанной в треугольник, называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности.

Рис. 5
Следствие. В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности, удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения |
| Произвольный треугольник |  | Посмотреть вывод формулы | a, b, c – стороны треугольника, . |
Посмотреть вывод формулы | |||
| Равнобедренный треугольник |  | Посмотреть вывод формулы | a – боковая сторона равнобедренного треугольника, |
| Равносторонний треугольник |  | Посмотреть вывод формулы | a – сторона равностороннего треугольника, |
| Прямоугольный треугольник |  | Посмотреть вывод формул | a, b – катеты прямоугольного треугольника, |
| Произвольный треугольник | |
 | где Посмотреть вывод формулы |
где Посмотреть вывод формулы | |
| Равнобедренный треугольник | |
 | где Посмотреть вывод формулы |
| Равносторонний треугольник | |
 | где Посмотреть вывод формулы |
| Прямоугольный треугольник | |
 | где Посмотреть вывод формул |
| Произвольный треугольник |
 где Посмотреть вывод формулы |
 где Посмотреть вывод формулы |
| Равнобедренный треугольник |
 где Посмотреть вывод формулы |
| Равносторонний треугольник |
 где Посмотреть вывод формулы |
| Прямоугольный треугольник |
 где Посмотреть вывод формулы |
Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, – полупериметр (рис. 6).

Рис. 6
Доказательство. Из формулы
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).

Рис. 7
Доказательство. Поскольку для произвольного треугольника справедлива формула
где
то, в случае равнобедренного треугольника, когда
получаем
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).

Рис. 8
Доказательство. Поскольку для равнобедренного треугольника справедлива формула
то, в случае равностороннего треугольника, когда
b = a,
получаем
что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
где a, b – катеты прямоугольного треугольника, c – гипотенуза, r – радиус вписанной окружности.
Доказательство. Рассмотрим рисунок 9.

Рис. 9
Поскольку четырёхугольник CDOF является прямоугольникомпрямоугольником, у которого соседние стороны DO и OF равны, то этот прямоугольник – квадратквадрат. Следовательно,
СD = СF= r,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание. Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник
Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника (рис. 8.106).
Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности (рис. 8.107).

Свойства вписанной окружности
1. Окружность можно вписать в любой треугольник.
2. Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны.
Например, на рисунке 8.106  .
.
Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.
Свойства описанной окружности
1. Окружность можно описать около любого треугольника.
2. Окружность можно описать около четырехугольника, если суммы его противолежащих углов равны.
Например, на рисунке 8.107  .
.
Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.
Расположение центров окружностей, описанных около треугольника:
1) центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника;
2) если треугольник остроугольный, то центр окружности расположен в этом треугольнике:
а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108);
б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);
3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);
4) если треугольник тупоугольный, то центр окружности расположен вне треугольника (рис. 8.111).

Расположение центров окружностей, вписанных в треугольник:
1) центр окружности, вписанной в треугольник, расположен в этом треугольнике (рис. 8.112 – 8.115);
2) центром окружности является точка пересечения биссектрис треугольника;
3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.

Формулы для вычисления радиусов вписанной и описанной окружностей
Радиус окружности, описанной около многоугольника, как правило, обозначают  , а радиус окружности, вписанной в многоугольник, обозначают
, а радиус окружности, вписанной в многоугольник, обозначают  :
:
1) для равностороннего треугольника со стороной  :
:
 , (8.34)
, (8.34)
 ; (8.35)
; (8.35)
2) для произвольного треугольника со сторонами  и площадью
и площадью  :
:
 , (8.36)
, (8.36)
 ; (8.37)
; (8.37)
3) для прямоугольного треугольника с катетами  и гипотенузой
и гипотенузой  :
:
 , (8.38)
, (8.38)
 ; (8.39)
; (8.39)
4) для квадрата со стороной  и диагональю
и диагональю  :
:
 , (8.40)
, (8.40)
 ; (8.41)
; (8.41)
5) для прямоугольника с диагональю  :
:
 ; (8.42)
; (8.42)
6) для ромба с высотой  :
:
 ; (8.43)
; (8.43)
7) для трапеции с высотой  , при условии, что в трапецию можно вписать окружность:
, при условии, что в трапецию можно вписать окружность:
 . (8.44)
. (8.44)
Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами  и площадью
и площадью  , по формуле
, по формуле  найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);
найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);
8) для правильного шестиугольника со стороной  :
:
 , (8.45)
, (8.45)
 . (8.46)
. (8.46)
Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка  является центром вписанной в него и описанной около него окружностей.
является центром вписанной в него и описанной около него окружностей.

Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна  .
.
Решение. Так как площадь круга радиуса  находят по формуле 8.32, а площадь квадрата со стороной
находят по формуле 8.32, а площадь квадрата со стороной  находят по формуле
находят по формуле  , то согласно условию задачи запишем:
, то согласно условию задачи запишем:  ,
,  .
.
А так как  , то
, то  ,
,  ,
,  ,
,  ,
,  .
.
Ответ:  .
.
Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника.

Решение. Площадь прямоугольника со смежными сторонами  и
и  находят по формуле
находят по формуле  .
.
Пусть  , тогда
, тогда  (рис. 8.118).
(рис. 8.118).
Получим:  ,
,  , откуда
, откуда  , следовательно,
, следовательно,  ,
,  .
.
По теореме Пифагора найдем диагональ прямоугольника:  ,
,  . Согласно формуле 8.42
. Согласно формуле 8.42  .
.
Ответ:  .
.
Пример 3. Найдите радиус окружности, вписанной в ромб, если его диагонали равны 6 и 8.

Решение. По теореме Пифагора найдем сторону ромба (рис. 8.119):
 ,
,  ,
,  .
.
По формуле 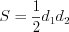 найдем площадь ромба:
найдем площадь ромба:  .
.
Но площадь ромба можно найти и по формуле  , а так как
, а так как  , то
, то  . Тогда
. Тогда  , а
, а  .
.
Ответ: 2,4.
Пример 4. Найдите длину окружности, вписанной в правильный треугольник, если его площадь равна  .
.
Решение. Площадь правильного треугольника со стороной  находят по формуле:
находят по формуле: 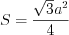 .
.
Зная площадь треугольника, найдем его сторону:  ,
,  ,
,
