В какой платежной матрице задачи о назначениях содержится оптимальный план

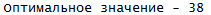
Модуль 3. v3. Целочисленное программирование.

Экстремальная задача линейного программирования, в которой на решение налагается целочисленность всех компонент, называется …
Целочисленной задачей

Целая часть числа (3,25-1,05) равна …
2

Если в оптимальном плане несколько дробных , то при применении метода Гомори дополнительное ограничение вводится для …
наибольшего

Целая часть числа (-45/8) равна …
-6

Целая часть числа 45/8 равна
5

Дробная часть числа (-87/25) равна …
13/25

Экстремальная задача линейного программирования, в которой на решение налагается целочисленность , является задачей …
Целочисленного программирования

Целая часть числа (-13,457) равна …
-14

К задачам целочисленного программирования относится …
Задача о назначениях

К задачам целочисленного программирования относится …
Задача о рюкзаке

К задачам целочисленного программирования не относится …
Задача о диете

При решении задачи венгерским методом получена матрица
Каким является решение в этой матрице?
0. 2 4 2
0 0 4 0.
0 1 0. 1
4 0. 0 0
Ответы: Полный и Оптимальный

При решении задачи венгерским методом получена матрица
Каким является решение в этой матрице?
4 0. 2
0. 1 0
1 0 1
Ответы: Неполный и Не оптимальный

К задачам целочисленного программирования относится …
Задача о коммивояжере

К задачам целочисленного программирования не относится …
Задача о составлении плана производства
либо
Транспортная задача

Дробная часть числа (-1,33) равна …
0,67

Дробная часть числа 17/4 равна
1/4

Дробная часть числа 1,26 равна …
0,26

В какой платежной матрице задачи о назначениях содержится не оптимальный план?
4 0. 2
0. 1 0
1 0 1

Целая часть числа (-1,4) равна …
-2

В какой платежной матрице задачи о назначениях содержится оптимальный план?
0. 2 4 2
0 0 4 0.
0 1 0. 1
4 0. 0 0

В какой платежной матрице задачи о назначениях содержится оптимальный план?
0 2 2 2
0 1 2 0
2 3 0 3
6 0 0 2

Целая часть числа 13,457 равна …
13

Экстремальная задача линейного программирования, в которой на решение налагается целочисленность нескольких компонент, называется …
Частично целочисленной задачей

Метод, заключающийся в упорядоченном переборе вариантов и рассмотрении лишь тех из них, которые оказываются по определенным признакам перспективными, и отбрасывании бесперспективных вариантов, называется …
Методом ветвей и границ

Общий метод решения задач целочисленного программирования, основанный на симплексном методе, называется
Методом Гомори

Добавлено через 19 часов 28 минут
Модуль 4. v3. Теория игр.

Вопрос 1
Пара чистых стратегий создает в игре ситуацию равновесия тогда и только тогда, когда в матрице выигрышей существует элемент , который одновременно является наибольшим в своем столбце и наименьшим в своей строке. Этот элемент (если он существует) называется … точкой.
оптимальной
седловой
проигрышной

выигрышной (не верный)

Вопрос 2
Критерий выбора оптимальной стратегии из предположения, что природа всегда будет действовать наихудшим для человека способом, т.е. выбирается элемент
, называется …
Критерием Вальда

Вопрос 3
Стратегия … игрока называется оптимальной, если при ее применении проигрыш второго игрока не может быть увеличен, какими бы стратегиями ни пользовался первый игрок.
второго

Вопрос 4
Цена матричной игры с платежной матрицей
12 7 8 15
13 9 9 14
15 12 11 16
11 10 9 7 равна … (ввести число).
11

Вопрос 5
Нормальная форма игры двух участников состоит из … платежных (ой) матриц(ы), показывающих(ей), какую сумму получит каждый из игроков при любой из возможных пар стратегий.
Двух

Вопрос 6
Цена матричной игры с платежной матрицей
10 20 15
40 30 20
30 10 20
равна … (ввести число).
20

Вопрос 7
Стратегия … игрока называется оптимальной, если при ее применении выигрыш первого игрока не может быть уменьшен, какими бы стратегиями ни пользовался второй.
первого

Вопрос 8
Критерий выбора оптимальной стратегии из предположения, что выбирается элемент
,где ,называется …
Критерием Сэвиджа

Вопрос 9
Игра, заключающаяся в том, что рассматриваются все возможные стратегии игроков и определяются платежи, соответствующие любой возможной комбинации стратегий игроков, называется …
игрой в нормальной форме

Вопрос 10
Каждая формализованная игра характеризуется:
количеством игроков, наборами стратегий, функциями выигрыша, результатом игры

Вопрос 11
Величина a=b=v называется …
ценой игры

Вопрос 12
Верхняя цена матричной игры, заданной платежной матрицей
1 5
4 3 ,равна
4

Вопрос 13
Верхняя цена матричной игры, заданной платежной матрицей
2 4
5 3 ,равна
4

Вопрос 14
Игра из двух игроков называется … , если один из игроков выигрывает ровно столько, сколько проигрывает другой. В таких играх интересы ее участников прямо противоположны друг другу.
антагонистической

Вопрос 15
Нижняя цена матричной игры, заданной платежной матрицей
1 4
3 2 ,равна
2

Вопрос 16
Цена матричной игры с платежной матрицей
3 7 4
5 8 9
6 2 3, лежит в интервалах
[5;6]

Вопрос 17
Критерий выбора оптимальной стратегии из предположения, что природа всегда будет действовать наилучшим для человека способом, т.е. выбирается элемент , называется …
Критерием максимума

Вопрос 18
Как называется принцип, в соответствии с которым каждый игрок, считая своего партнера по игре разумным противником, выбирает свои стратегии исходя из предположения, что его противник не упустит ни единой возможности использовать любую его ошибку в своих интересах?
принцип осторожности

Вопрос 19
В антагонистической игре сумма выигрышей первого и второго игрока равна …
Нулю

Вопрос 20
Критерий выбора оптимальной стратегии из предположения, что выбирается элемент ,
где – степень оптимизма, , называется …
Критерием Гурвица

Вопрос 21
Нижняя цена матричной игры, заданной платежной матрицей
1 5
4 3 , равна
3

Вопрос 22
Верхняя цена матричной игры, заданной платежной матрицей
1 6
5 4 , равна
5

Вопрос 23
Нижняя цена матричной игры, заданной платежной матрицей
2 5
6 4 , равна
4

Вопрос 24
Величина a=max min h называется …
нижней ценой игры

Вопрос 25
Верхняя цена матричной игры, заданной платежной матрицей
1 4
3 2 , равна
2

Вопрос 26
Чистые стратегии, взятые в случайном порядке с некоторыми вероятностями, называются …
смешанными стратегиями

Вопрос 27
Критерий выбора оптимальной стратегии из предположения, что выбирается элемент , называется …
Критерием Сэвиджа

Вопрос 28
Величина B = minmaxh называется …
верхней ценой игры

Источник

Экстремальная задача линейного программирования, в которой на решение налагается целочисленность , является задачей …

Выберите один ответ:

Целочисленного программирования

Особенного программирования

Рационального программирования

Динамического программирования

В какой платежной матрице задачи о назначениях содержится не оптимальный план?

Выберите один ответ:

Дробная часть числа 17/4 равна …

Выберите один ответ:

1/4

3/4

Целая часть числа (3,25-1,05) равна …

Выберите один ответ:

Дробная часть числа 1,26 равна …

Выберите один ответ:

-0,74

0,26

0,74

-0,26

В какой платежной матрице задачи о назначениях содержится оптимальный план?

Выберите один ответ:

Целая часть числа (-1,4) равна …

Выберите один ответ:

-1

-2

Общий метод решения задач целочисленного программирования, основанный на симплексном методе, называется

Выберите один ответ:

Методом ветвей и границ

Методом потенциалов

Методом Гомори

Венгерским методом

Целая часть числа (-45/8) равна …

Выберите один ответ:

-40

-41

-6

-5

Целая часть числа (-13,457) равна …

Выберите один ответ:

-13

-14

Целая часть числа 45/8 равна …

Выберите один ответ:

Дробная часть числа (-87/25) равна …

Выберите один ответ:

-12/25

-13/25

13/25

12/25

Дробная часть числа (-1,33) равна …

Выберите один ответ:

0,33

-0,67

-0,33

0,67

При решении задачи венгерским методом получена матрица

Каким является решение в этой матрице?

Выберите один или несколько ответов:

Оптимальный

Полный

Неполный

Не оптимальный

Выберите один ответ:

Методом Фогеля

Венгерским методом

Методом Гомори

Методом ветвей и границ

Если в оптимальном плане несколько дробных , то при применении метода Гомори дополнительное ограничение вводится для …

Выберите один ответ:

среднего

любого

наибольшего

наименьшего

Экстремальная задача линейного программирования, в которой на решение налагается целочисленность всех компонент, называется …

Выберите один ответ:

Рациональной задачей

Целочисленной задачей

Частично целочисленной задачей

Натуральной задачей

Экстремальная задача линейного программирования, в которой на решение налагается целочисленность нескольких компонент, называется …

Выберите один ответ:

Целочисленной задачей

Частично целочисленной задачей

Рациональной задачей

Натуральной задачей

Целая часть числа 13,457 равна …

Выберите один ответ:

-13

-14

К задачам целочисленного программирования не относится …

Правильные ответы:

Задача о составлении плана производства

Задача о диете

Транспортная задача

К задачам целочисленного программирования относится …

Правильные ответы:

Задача о назначениях

Задача о рюкзаке

Задача о коммивояжере

При решении задачи венгерским методом получена матрица

Каким является решение в этой матрице?

Выберите один или несколько ответов:

Неполный

Не оптимальный

Оптимальный

Полный

В какой платежной матрице задачи о назначениях содержится оптимальный план?

ТЕОРИЯ ИГР

Стратегия ________ игрока называется оптимальной, если при ее применении проигрыш второго игрока не может быть увеличен, какими бы стратегиями ни пользовался первый игрок.

Выберите один ответ:

первого

второго

Верхняя цена матричной игры, заданной платежной матрицей , равна …

Выберите один ответ:

Чистые стратегии, взятые в случайном порядке с некоторыми вероятностями, называются …

Выберите один ответ:

основными стратегиями

смешанными стратегиями

альтернативными стратегиями

вероятностными стратегиями

Критерий выбора оптимальной стратегии из предположения, что природа всегда будет действовать наилучшим для человека способом, т.е. выбирается элемент , называется …

Выберите один ответ:

Критерием Вальда

Критерием максимума

Критерием Гурвица

Критерием Сэвиджа

Пара чистых стратегий создает в игре ситуацию равновесия тогда и только тогда, когда в матрице выигрышей существует элемент , который одновременно является наибольшим в своем столбце и наименьшим в своей строке. Этот элемент (если он существует) называется …

Выберите один ответ:

Седловой точкой

Выигрышной точкой

Проигрышной точкой

Оптимальной точкой

Критерий выбора оптимальной стратегии из предположения, что выбирается элемент , называется …

Выберите один ответ:

Критерием максимума

Критерием Вальда

Критерием Гурвица

Критерием Сэвиджа

Верхняя цена матричной игры, заданной платежной матрицей , равна …

Выберите один ответ:

В антагонистической игре сумма выигрышей первого и второго игрока равна …

Выберите один ответ:

Нулю

Одному

Двум

Трем

Игра, заключающаяся в том, что рассматриваются все возможные стратегии игроков и определяются платежи, соответствующие любой возможной комбинации стратегий игроков, называется …

Выберите один ответ:

игрой в стандартной форме

игрой в канонической форме

игрой в произвольной форме

игрой в нормальной форме

Нижняя цена матричной игры, заданной платежной матрицей , равна …

Выберите один ответ:

Как называется принцип, в соответствии с которым каждый игрок, считая своего партнера по игре разумным противником, выбирает свои стратегии исходя из предположения, что его противник не упустит ни единой возможности использовать любую его ошибку в своих интересах?

Выберите один ответ:

принцип эквивалентности

принцип оптимальности

принцип осторожности

принцип системности

Текст вопроса

Величина называется …

Выберите один ответ:

ценой игры

выигрышем

верхней ценой игры

нижней ценой игры

Верхняя цена матричной игры, заданной платежной матрицей , равна …

Выберите один ответ:

Величина называется …

Выберите один ответ:

нижней ценой игры

верхней ценой игры

выигрышем

ценой игры

Верхняя цена матричной игры, заданной платежной матрицей , равна …

Выберите один ответ:

Цена матричной игры с платежной матрицей равна …

Выберите один ответ:

Нижняя цена матричной игры, заданной платежной матрицей , равна …

Выберите один ответ:

Критерий выбора оптимальной стратегии из предположения, что природа всегда будет действовать наихудшим для человека способом, т.е. выбирается элемент , называется …

Выберите один ответ:

Критерием Сэвиджа

Критерием максимума

Критерием Вальда

Критерием Гурвица

Нижняя цена матричной игры, заданной платежной матрицей , равна …

Выберите один ответ:

Каждая формализованная игра характеризуется:

Выберите один ответ:

биматрицей

выигрышем

количеством игроков, наборами стратегий, функциями выигрыша, результатом игры

матрицей

Нормальная форма игры двух участников состоит из ________ платежных (ой) матриц(ы), показывающих(ей), какую сумму получит каждый из игроков при любой из возможных пар стратегий.

Выберите один ответ:

Двух

Трех

Одной

Четырех

Цена матричной игры с платежной матрицей лежит в интервалах …

Выберите один ответ:

[2;7]

[2;9]

[5;6]

[3;7]

Пару слов о методе

Для того чтобы не расписывать много теории с математическими терминами и определениями, предлагаю рассмотреть пару вариантов построения задачи о назначениях, и я думаю Вы сразу поймете в каких случаях применим Венгерский метод:

Задача о назначении работников на должности. Необходимо распределить работников на должности так, чтобы достигалась максимальная эффективность, или были минимальные затраты на работу.
Назначение машин на производственные секции. Распределение машин так, чтобы при их работе производство было максимально прибыльным, или затраты на их содержание минимальны.
Выбор кандидатов на разные вакансии по оценкам. Этот пример разберем ниже.

Как Вы видите, вариантов для которых применим Венгерский метод много, при этом подобные задачи возникают во многих сферах деятельности.

В итоге задача должна быть решена так, чтобы один исполнитель (человек, машина, орудие, …) мог выполнять только одну работу, и каждая работа выполнялась только одним исполнителем.

Необходимое и достаточное условие решения задачи – это ее закрытый тип. Т.е. когда количество исполнителей = количеству работ (N=M). Если же это условие не выполняется, то можно добавить вымышленных исполнителей, или вымышленные работы, для которых значения в матрице будут нулевыми. На решение задачи это никак не повлияет, лишь придаст ей тот необходимый закрытый тип.

Step-by-step алгоритм на примере

Постановка задачи: Пусть намечается важная научная конференция. Для ее проведения необходимо настроить звук, свет, изображения, зарегистрировать гостей и подготовиться к перерывам между выступлениями. Для этой задачи есть 5 организаторов. Каждый из них имеет определенные оценки выполнения той, или иной работы (предположим, что эти оценки выставлены как среднее арифметическое по отзывам их сотрудников). Необходимо распределить организаторов так, чтобы суммарная их оценка была максимальной. Задача имеет следующий вид:

Если задача решается на максимум (как в нашем случае), то в каждой строке матрицы необходимо найти максимальный элемент, его же вычесть из каждого элемента соответствующей строки и умножить всю матрицу на -1. Если задача решается на минимум, то этот шаг необходимо пропустить.

В каждой строке и в каждом столбце должен быть только один выбранный ноль. (т.е. когда выбрали ноль, то остальные нули в этой строке или в этом столбце уже не берем в расчет). В этом случае это сделать невозможно:

(Если задача решается на минимум, то необходимо начинать с этого шага). Продолжаем решение далее. Редукция матрицы по строкам (ищем минимальный элемент в каждой строке и вычитаем его из каждого элемента соответственно):

Т.к. все минимальные элементы – нулевые, то матрица не изменилась. Проводим редукцию по столбцам:

Опять же смотрим чтобы в каждом столбце и в каждой строке был только один выбранный ноль. Как видно ниже, в данном случае это сделать невозможно. Представил два варианта как можно выбрать нули, но ни один из них не дал нужный результат:

Продолжаем решение дальше. Вычеркиваем строки и столбцы, которые содержат нулевые элементы (ВАЖНО! Количество вычеркиваний должно быть минимальным). Среди оставшихся элементов ищем минимальный, вычитаем его из оставшихся элементов (которые не зачеркнуты) и прибавляем к элементам, которые расположены на пересечении вычеркнутых строк и столбцов (то, что отмечено зеленым – там вычитаем; то, что отмечено золотистым – там суммируем; то, что не закрашено – не трогаем):

Как теперь видно, в каждом столбце и строке есть только один выбранный ноль. Решение задачи завершаем!

Подставляем в начальную таблицу месторасположения выбранных нулей. Таким образом мы получаем оптимум, или оптимальный план, при котором организаторы распределены по работам и сумма оценок получилась максимальной:

Если же вы решаете задачу и у вас до сих пор невозможно выбрать нули так, чтобы в каждом столбце и строке был только один, тогда повторяем алгоритм с того места где проводилась редукция по строкам (минимальный элемент в каждой строке).

Реализация на языке программирования R

Венгерский алгоритм реализовал с помощью рекурсий. Буду надеяться что мой код не будет вызывать трудностей. Для начала необходимо скомпилировать три функции, а затем начинать расчеты.

Данные для решения задачи берутся из файла example.csv который имеет вид:

Код добавил в спойлер ибо статья была бы слишком большой из-за него

#Подключаем библиотеку для удобства расчетов
library(dplyr)

#Считываем csv фаил (первый столбик – названия строк; первая строка – названия столбцов)
table <- read.csv(“example.csv”,header=TRUE,row.names=1,sep=”;”)

#Проводим расчеты
unique_index <- hungarian_algorithm(table,T)

#Выводим
cat(paste(row.names(table[as.vector(unique_index$row),]),” – “,names(table[as.vector(unique_index$col)])),sep = “n”)

#Считаем оптимальный план
cat(“Оптимальное значение -“,sum(mapply(function(i, j) table[i, j], unique_index$row, unique_index$col, SIMPLIFY = TRUE)))

#____________________Алгоритм венгерского метода__________________________________

hungarian_algorithm <- function(data,optim=F){

#Если optim = T, то будет искаться максимальное оптимальное значение
if(optim==T)
{
data <- data %>%
apply(1,function(x) (x-max(x))*(-1)) %>%
t() %>%
as.data.frame()
optim <- F
}

#Редукция матрицы по строкам
data <- data %>%
apply(1,function(x) x-min(x)) %>%
t() %>%
as.data.frame()

#Нахождение индексов всех нулей
zero_index <- which(data==0, arr.ind = T)

#Нахождение всех “неповторяющихся” нулей слева-направо
unique_index <- from_the_beginning(zero_index)

#Если количество “неповторяющихся” нулей не равняется количеству строк в исходной таблице, то..
if(nrow(unique_index)!=nrow(data))
#..Ищем “неповторяющиеся” нули справа-налево
unique_index <- from_the_end(zero_index)

#Если все еще не равняется, то продолжаем алгоритм дальше
if(nrow(unique_index)!=nrow(data))
{

#Редукция матрицы по столбцам
data <- data %>%
apply(2,function(x) x-min(x)) %>%
as.data.frame()

zero_index <- which(data==0, arr.ind = T)
unique_index <- from_the_beginning(zero_index)

if(nrow(unique_index)!=nrow(data))
unique_index <- from_the_end(zero_index)

if(nrow(unique_index)!=nrow(data))
{

#”Вычеркиваем” строки и столбцы которые содержат нулевые элементы (ВАЖНО! количество вычеркиваний должно быть минимальным)
index <- which(apply(data,1,function(x) length(x[x==0])>1))
index2 <- which(apply(data[-index,],2,function(x) length(x[x==0])>0))

#Среди оставшихся элементов ищем минимальный
min_from_table <- min(data[-index,-index2])

#Вычитаем минимальный из оставшихся элементов
data[-index,-index2] <- data[-index,-index2]-min_from_table

#Прибавляем к элементам, расположенным на пересечении вычеркнутых строк и столбцов
data[index,index2] <- data[index,index2]+min_from_table

zero_index <- which(data==0, arr.ind = T)
unique_index <- from_the_beginning(zero_index)

if(nrow(unique_index)!=nrow(data))
unique_index <- from_the_end(zero_index)

#Если все еще количество “неповторяющихся” нулей не равняется количеству строк в исходной таблице, то..
if(nrow(unique_index)!=nrow(data))
#..Повторяем весь алгоритм заново
hungarian_algorithm(data,optim)

else
#Выводим индексы “неповторяющихся” нулей
unique_index
}
else
#Выводим индексы “неповторяющихся” нулей
unique_index
}
else
#Выводим индексы “неповторяющихся” нулей
unique_index
}
#_________________________________________________________________________________

#__________Функция для нахождения “неповторяющихся” нулей слева-направо___________

from_the_beginning <- function(x,i=0,j=0,index = data.frame(row=numeric(),col=numeric())){

#Выбор индексов нулей, которые не лежат на строках i, и столбцах j
find_zero <- x[(!x[,1] %in% i) & (!x[,2] %in% j),]

if(length(find_zero)>2){

#Записываем индекс строки в вектор
i <- c(i,as.vector(find_zero[1,1]))

#Записываем индекс столбца в вектор
j <- c(j,as.vector(find_zero[1,2]))

#Записываем индексы в data frame (это и есть индексы уникальных нулей)
index <- rbind(index,setNames(as.list(find_zero[1,]), names(index)))

#Повторяем пока не пройдем по всем строкам и столбцам
from_the_beginning(find_zero,i,j,index)}
else
rbind(index,find_zero)
}
#_________________________________________________________________________________

#__________Функция для нахождения “неповторяющихся” нулей справа-налево___________

from_the_end <- function(x,i=0,j=0,index = data.frame(row=numeric(),col=numeric())){
find_zero <- x[(!x[,1] %in% i) & (!x[,2] %in% j),]
if(length(find_zero)>2){
i <- c(i,as.vector(find_zero[nrow(find_zero),1]))
j <- c(j,as.vector(find_zero[nrow(find_zero),2]))
index <- rbind(index,setNames(as.list(find_zero[nrow(find_zero),]), names(index)))
from_the_end(find_zero,i,j,index)}
else
rbind(index,find_zero)
}
#_________________________________________________________________________________

Результат выполнения программы:

В завершение

Спасибо большое что потратили время на чтение моей статьи. Все используемые ссылки предоставлю ниже. Надеюсь, Вы узнали что-то для себя новое или обновили старые знания. Всем успехов, добра и удачи!

Используемые ресурсы

1. Штурмовал википедию
2. И другие хорошие сайты
3. Подчеркнул для себя немного информации с этой статьи

Источник