Свойство биссектрисы треугольника какой класс
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 марта 2020;
проверки требуют 11 правок.
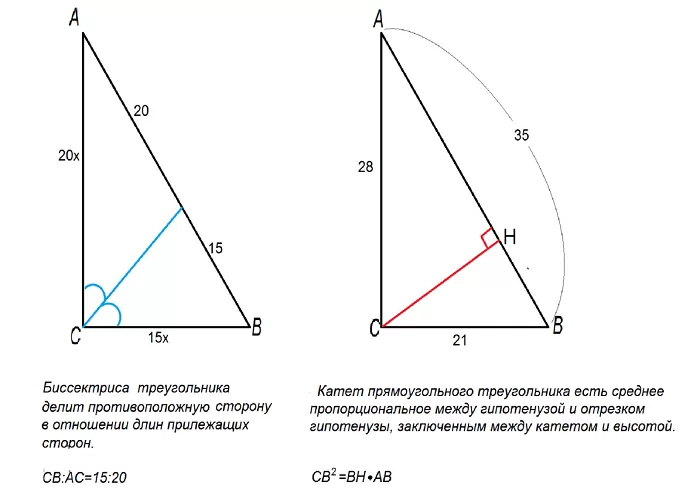
Биссектриса AD делит пополам угол A
Биссектри́са (от лат. bi- «двойное», и sectio «разрезание») угла — луч, исходящий из вершины угла и делящий этот угол на два равных угла. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла[1].
Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. У треугольника существуют три биссектрисы, соответствующие трём его вершинам.
Связанные определения
- Точка пересечения биссектрисы угла треугольника с его стороной, не являющейся стороной этого угла, называется основанием биссектрисы.
Свойства
Свойства точек пересечения биссектрис
- Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности (инцентре).
- Биссектрисы одного внутреннего и двух внешних углов треугольника пересекаются в одной точке. Эта точка — центр одной из трёх вневписанных окружностей этого треугольника.
- Каждая биссектриса треугольника делится точкой пересечения биссектрис в отношении суммы прилежащих сторон к противолежащей, считая от вершины.
- Гипербола Фейербаха — описанная гипербола, проходящая через ортоцентр и центр вписанной окружности (он же — инцентр или точка пресечения внутренних биссектрис треугольника). Её центр лежит в точке Фейербаха. Подерные и чевианные окружности точек на гиперболе Фейербаха проходят через точку Фейербаха.
Свойства, связанные с углами
- Каждая внутренняя (внешняя) биссектриса угла треугольника, выходящая из его вершины, делит этот внутренний (внешний) угол треугольника пополам (на две равные половинки).
- Угол между биссектрисами двух смежных углов (между внутренними и внешними биссектрисами углов треугольника при одной вершине) равен 90 градусам.
- Внутренняя биссектриса угла треугольника изогонально сопряжена самой себе.
Свойства, связанные с дугами
- Свойство биссектрисы вписанного угла: биссектриса вписанного угла делит на две равные части дугу, на которую этот угол опирается.
- То же свойство верно и для биссектрисы центрального угла.
Свойства биссектрис равнобедренного треугольника
- Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья биссектриса одновременно является медианой и высотой того угла, из которого она выходит.
- Верно и обратное: в равнобедренном треугольнике две биссектрисы равны, и третья биссектриса одновременно является медианой и высотой.
- В равнобедренном треугольнике внутренняя биссектриса угла, противоположного основанию треугольника, является медианой и высотой.
- Одна и только одна биссектриса внешнего угла неравностороннего треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный.
- У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам.
- У равностороннего треугольника все три внутренние биссектрисы равны.
Свойства оснований биссектрис
- Теорема о биссектрисе (см. рис.): Биссектриса внутреннего угла треугольника делит противоположную сторону (то есть делит своим основанием противоположную сторону) в отношении, равном отношению двух прилежащих сторон. То есть или .
- Теорема о биссектрисе — частный случай теоремы Штейнера.
- Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника (Одна и только одна биссектриса внешнего угла треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный. У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам. Других возможностей нет).
- Биссектриса внутреннего угла треугольника делит противоположную сторону изотомически по отношению к антибиссектрисе того же угла.
- Окружности, построенные, как на диаметре, на отрезке, соединяющем основания внутренней и внешней биссектрисы, выпущенных из одного угла, проходят через точки Аполлония.
- Через точку Фейербаха проходит окружность, проведённая через основания биссектрис .[4]
Свойства осей биссектрис
- Если биссектрисы внешних углов треугольника не параллельны противоположным сторонам, то их основания лежат на одной прямой, называемой осью внешних биссектрис.
- Точка Лемуана треугольника лежит на прямой Обера четырёхсторонника, образованного четырьмя осями биссектрис.
Другие свойства
- Если треугольник разносторонний (неравносторонний), то внутренняя биссектриса, проведённая из любой его вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины.
- Расстояния от сторон угла до любой точки биссектрисы одинаковы.
- Построение треугольника по трем заданным биссектрисам с помощью циркуля и линейки невозможно,[5] причём даже при наличии трисектора.[6]
- Три внешние биссектрисы любого треугольника пересекаются в трёх разных точках, которые являются центрами вневписанных окружностей исходного треугольника или вершинами так называемого треугольника трёх внешних биссектрис исходного треугольника[7].
Длина биссектрис в треугольнике
Для выведения нижеприведённых формул можно воспользоваться теоремой Стюарта.
, где — полупериметр.
Для трёх биссектрис углов , и с длинами соответственно и , справедлива формула[8]
,
,
где:
- — стороны треугольника против вершин соответственно,
- — внутренние углы треугольника при вершинах соответственно,
- — высота треугольника, опущенная на сторону .
- — длина внутренней биссектрисы, проведённой к стороне ,
- — длины отрезков, на которые внутренняя биссектриса делит сторону ,
- — длина внешней биссектрисы, проведённой из вершины к продолжению стороны .
- — длины отрезков, на которые внешняя биссектриса делит сторону и её продолжение до основания самой биссектрисы.
- Если медиана , высота и внутренняя биссектриса выходят из одной и той же вершины треугольника, около которого описана окружность радиуса , тогда[9]:p.122,#96
Длина частей биссектрис в треугольнике
Уравнения биссектрис
Мнемоническое правило (шуточное)
- Биссектриса — это крыса, которая бегает по углам и делит угол пополам.
См. также
- Антибиссектриса
- Высота (геометрия)
- Высота треугольника
- Инцентр
- Медиана треугольника
- Симедиана
- Теорема о биссектрисе
- Ось внешних биссектрис или антиортовая ось
- Треугольник
- Треугольник трёх внешних биссектрис
- Центроид
- Чевиана
Примечания
- ↑ Иванов А. Б. Биссектриса угла // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия, 1977. — Т. 1. — С. 496. — 576 с. — 150 000 экз.
- ↑ Kimberling, Clark (1994), Central Points and Central Lines in the Plane of a Triangle, Mathematics Magazine Т. 67 (3): 163–187, DOI 10.2307/2690608.
- ↑ v. Nagel, C. H. (1836), Untersuchungen über die wichtigsten zum Dreiecke gehörenden Kreise, Leipzig.
- ↑ Акопян А. В., Заславский А. А.. Геометрические свойства кривых второго порядка. — 2-е изд., дополн.. — 2011. — С. 105.
- ↑ Кто и когда доказал невозможность построения треугольника по трем биссектрисам?. Дистанционный консультационный пункт по математике МЦНМО.
- ↑ Можно ли построить треугольник по трем биссектрисам, если кроме циркуля и линейки разрешается использовать трисектор. Дистанционный консультационный пункт по математике МЦНМО.
- ↑ Стариков В. Н. Исследования по геометрии// Сборник публикаций научного журнала Globus по материалам V-й международной научно-практической конференции «Достижения и проблемы современной науки» г. Санкт-Петербург: сборник со статьями (уровень стандарта, академический уровень). С-П.: Научный журнал Globus, 2016. С. 99-100
- ↑ Simons, Stuart. Mathematical Gazette 93, March 2009, 115—116.
- ↑ Altshiller-Court, Nathan, College Geometry, Dover Publ., 2007.
Литература
- Коган Б. Ю. Приложение механики к геометрии. — М.: Наука, 1965. — 56 с.
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 30-31. — ISBN 5-94057-170-0.
Источник
Базовым понятием и одним из наиболее интересных и полезных объектов школьной математики является биссектриса. С её помощью доказываются многие положения планиметрии, упрощается решение задач.
Известные свойства позволяют рассматривать геометрические фигуры с разных точек зрения. Появляется вариативность при выборе пути доказательств.
Становится возможным использование инструмента алгебры, например, свойство пропорции, нахождение неизвестных величин, решение алгебраических уравнений при рассмотрении геометрических вопросов.
Что такое биссектриса в геометрии
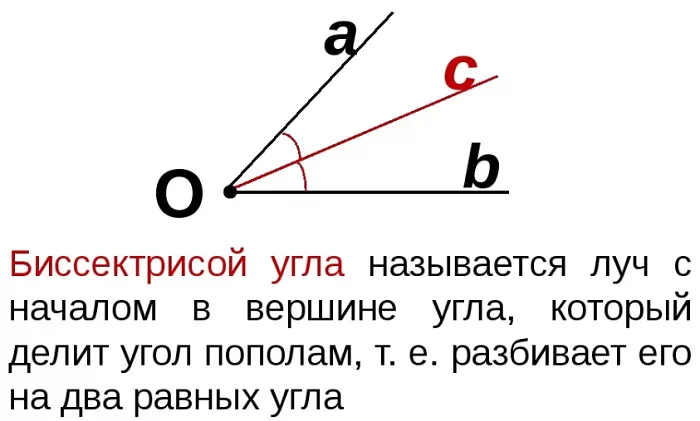
Рассматривают луч, выходящий из вершины угла или его часть (отрезок), который делит угол пополам. Такой луч (или, соответственно, отрезок) называется биссектрисой.
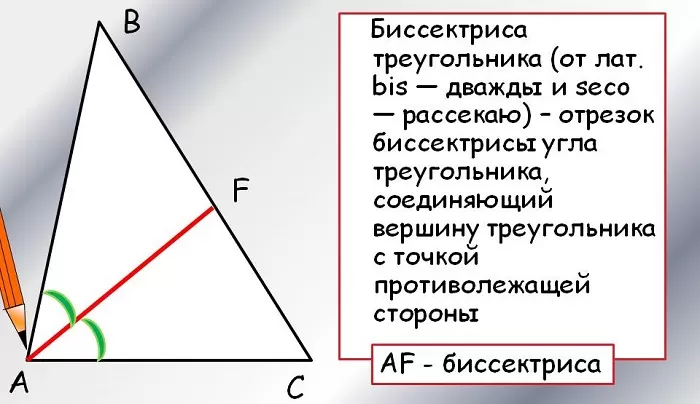
Часто для треугольников определение немного сужают, говоря об отрезке, соединяющем вершину угла, делящем его пополам, с точкой на противолежащей стороне. При этом рассматривается внутренняя область фигуры.
В то же время, часто при решении задач используются прямые, делящие внешние углы на два равных.
Биссектриса прямоугольного треугольника
Для прямоугольного треугольника одна из биссектрис образует равные углы, величины которых хорошо просчитываются (45 градусов).

Это помогает вычислять углы при решении задач, связанных с фигурами, которые можно представить в виде прямоугольных треугольников или прямоугольников.
В тупоугольном треугольнике биссектриса делит больший угол на равные части, величина которых меньше 900.
Свойства биссектрисы треугольника
1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.
2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон.
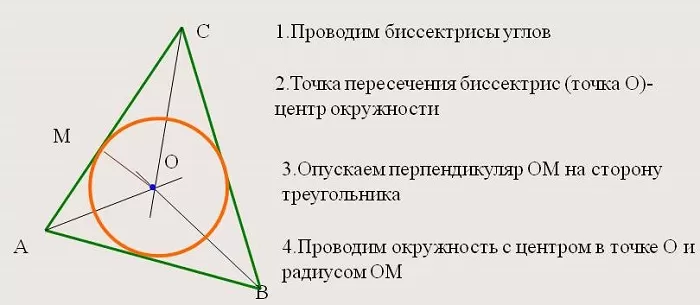
Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.
Благодаря этому утверждению, легко доказывается следующее правило:
Площадь описанного многоугольника равна:
S = p∗r
где p – полупериметр, а r – радиус вписанной окружности.
Это позволяет находить решение не только планиметрических, но и стереометрических задач.
Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;
3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.
Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;
4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.
В этом случае основание параллельно внешней биссектрисе.
Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;
5. Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;
6. У правильного треугольника все внешние биссектрисы параллельны сторонам;
7. Выделяют несколько особенностей, среди которых есть следующая теорема:
«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».
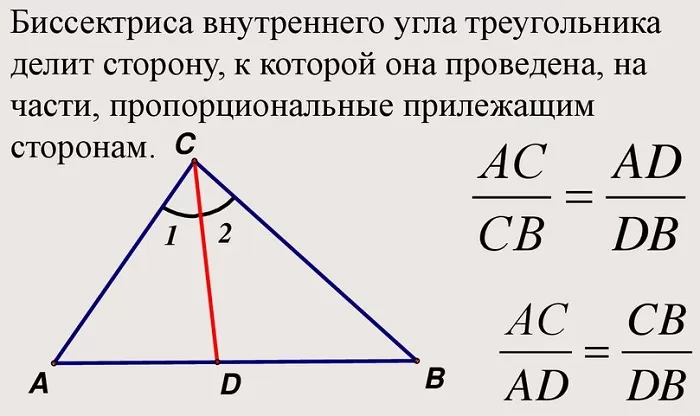
Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;
8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.
Все формулы биссектрисы в треугольнике
В зависимости от исходных данных, длина биссектрисы, проведённой к стороне C, lc, равна:

Примеры решения задач
Задача №1
В ΔABC ∠C = 90°, проведена биссектриса острого угла. Отрезок, соединяющий её основание с точкой пересечения медиан, перпендикулярен катету. Найти углы заданной фигуры.
Решение.
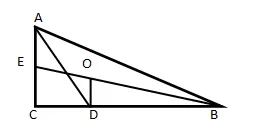
Пусть ∠ACB = 90°, AD – биссектриса, BE – медиана, O – точка пересечения медиан, OD⊥BC.
Тогда OE : OB = 1 : 2по свойству медиан.
Так как OD⊥BC, то ODIIOC, следовательно, ΔBOD ∼ ΔBEC по второму признаку подобия, поэтому, по свойству подобных фигур, CD : DB = 1 : 2.
Это означает, что CA : AB = 1 : 2.
Так как катет равен половине гипотенузы, то ∠ABC = 30°, откуда ∠CAB = 60°.
Ответ: 90°, 60°, 30°.
Задача №2
Диагональ параллелограмма делит его острый угол пополам. Доказать, что этот параллелограмм является ромбом.
Доказательство.
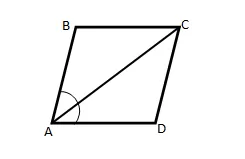
Так как ABCD – параллелограмм, то ∠DAC = ∠ACB, как накрест лежащие при параллельных прямых AD, BC и секущей AC.
По условию, ∠DAC = ∠ACB = ∠BAC, поэтому ΔACB равнобедренный, то есть AB = BC, следовательно, ABCD – ромб.
Доказано.
Источник
Мария Полютова
20 февраля 2019 · 15,4 K
Имею естественно научное образование, в юношестве прикипел к литературе, сейчас…
Основные свойства бисскетрисы:
- Делит противовположные стороны на части, которые пропорциональные прилегающим сторонам
- Все биссектрисы пересекаются в точке внутри треугольника, и эта точка является центром окружности, вписанной в треугольник
- Точки биссектрисы равноудалены от точек ее угла
- Бисскетрисы внешнего и внутреннего уголов прямоугольника являются перпендикулярными
- Бисскетриса является и медианой и высотой только в правильном треугольнике
Биссектриса является медийной и высотой и в равнобедренном треугольнике
Геометрия как быстро выучить что такое треугольник высота медиана биссектриса?
Высота значит точно то же, что и в обычном мире 🙂 То есть расстояние от вершины (она может быть любой) до той линии, на которой треугольник “стоит”.
Медиана соединяет вершину с центром стороны напротив.
Биссектриса делит угол пополам, выходя из вершины “внутрь”.
Высоты – из вершин к плоскости, на которой треугольник может “стоять”. Тоесть под прямым углом сверху-вниз.
Медиана – делит сторону напротив угла пополам
Биссектриса – делит пополам сам угол
Прочитать ещё 2 ответа
Чему равно число Пи?
Никто не знает точно, чему равно пи. Если разделить длину окружности на ее диаметр, то результат всегда будет одинаковый, какую окружность ни возьми. Этот результат и обозначили греческой буквой пи. Буква понадобилась потому, что привычными цифрами это число точно записать невозможно. Но мы знаем, чему оно равно приблизительно.
Самое знаменитое приближение – 3,14. Чтобы запомнить больше цифр, можно выучить стишок:
Надо очень постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть
Прочитать ещё 17 ответов
В определении биссектрисы треугольника лежит то, что этот отрезок пересечет противоположную сторону треугольника, но почему? Где доказательство? С мат. точ.зр.
Веб-дизайнер, участник промо-группы, музыкант, фотограф, видеомейкер, предприним…
Не понимаю о чем вы спрашиваете, но биссектриса – это прямая, делящая угол пополам, проведенная от вершины угла до её пересечения с противолежащей стороной. Тут главное что она делит угол, а не то что она прикасается к стороне
Прочитать ещё 1 ответ
Какие четыре точки называют “замечательными точками” треугольника?
Замечательных точек треугольника много, все не перечесть 🙂
Четыре самые знаменитые, их изучают в школе:
- Центр масс — точка пересечения медиан треугольника
- Центр описанной около треугольника окружности — точка пересечения серединных перпендикуляров
- Центр вписанной в треугольник окружности — точка пересечения биссектрис
- Ортоцентр — точка пересечения высот треугольника
Вот еще примеры замечательных точек:
- Точка Жергонна — точка пересечения прямых, проходящих через точки касания вписанной окружности со сторонами треугольника и противолежащие вершины.
- Точка Нагеля — точка пересечения прямых, проходящих через точки касания вневписанных окружностей со сторонами треугольника и противолежащие вершины
- Точка Лемуана — точка, изогонально сопряжённая точке пересечения медиан, то есть точка пересечения прямых, симметричных медианам относительно соответствующих биссектрис треугольника
Есть еще много других
Прочитать ещё 1 ответ
Источник
Тема: Свойство биссектрисы угла.
Цели:Рассмотрение теоремы о свойстве биссектрисы угла и применение данной теоремы при решении задач.
Задачи:
1. Рассмотреть теорему о свойстве биссектрисы угла и её следствие.
2. Учить применять данные теоремы и следствие при решении задач.
3. Формировать умения применять известные знания в незнакомой ситуации, сравнивать, анализировать, обобщать.
4. Продолжать развивать познавательную активность, умение формулировать свои выводы и доказывать их.
5. Воспитывать уверенность в себе, познавательный интерес.
Оборудование: ПК, презентация, чертёжные инструменты.
Ход урока
I. Организационный момент. Объявление темы и постановка целей урока совместно с учащимися.
II. Проверка домашнего задания.
Визуально проверяется наличие домашнего задания в тетради
III. Актуализация опорных знаний
Для того, чтобы начать изучение нового материала, нам придётся опереться на уже изученный материал.
1. Какие линии в треугольнике вам известны? К числу линий, изучаемых в школьном курсе геометрии, относятся:
• высоты треугольника;
• медианы треугольника;
• биссектрисы треугольника;
• серединные перпендикуляры к сторонам треугольника.
2. Кто напомнит обобщенную теорему Фалеса?
Если на одной стороне угла отложить несколько отрезков и через их концы провести параллельные прямые, то на другой стороне угла отложатся отрезки, пропорциональные данным.
Повторение определений путём фронтальной беседы.
III. Мотивация изучения материала
В старших классах каждый школьник
Изучает треугольник.
Три каких-то уголка,
А работы на века.

И опять треугольник! Треугольник в геометрии играет особую роль. Без преувеличения можно сказать, что вся или почти вся геометрия строится на треугольнике.
IV. Изучение нового материала.

Доказательство:
V. Историческая справка.
Удивительно, но треугольник, несмотря на свою простоту, является неисчерпаемым объектом изучения – никто даже в наше время не осмелится сказать, что изучил и знает все свойства треугольника. (Слайд 3).
–А какие треугольники мы с вами рассматривали? (Слайд 4).
Ожидаемые ответы: равнобедренный, равносторонний, тупоугольный, прямоугольный, остроугольный.
–Сегодня мы с вами очень кратко ознакомимся с треугольниками, которые имеют своё собственное «имя», или носят имя того, кто их открыл или исследовал. (Слайд 4).
Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.Египетский треугольник с соотношением сторон 3:4:5 применялся египтянами землемерами и архитекторами для построения прямых углов. Несмотря на возраст, это способ построения прямого угла активно используется строителями и теперь. (Слайд 4, 6).
Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. (Слайды 4, 7).
Треугольник Рёло – это геометрическая фигура, образованная пересечением трёх равных кругов одинакового радиуса с центрами в вершинах равностороннего треугольника. Сверло, сделанное на основе треугольника Рёло, позволяет сверлить квадратные отверстия (с точностью в 2%). (Слайды 4, 8).
Один из самых загадочных и интересных треугольников – “Бермудский треугольник”. Еще это место называют аномальной зоной. На самом деле это место, которое традиционно считается самым ужасным, самым жутким местом планеты. Здесь бесследно исчезало множество кораблей и самолетов – большинство из них после 1945 года. Здесь погибло более тысячи человек. Однако при поисках никого и ничего не удалось обнаружить. Бермудский треугольник не имеет четких границ, нельзя найти на карте его точное обозначение. Разные ученые определяют его местоположение на свое усмотрение. Самое распространенное его определение – это область в Атлантическом океане между Бермудами, Пуэрто-Рико и Майами. Общая площадь – 1 млн. квадратных километров. Однако название этой области тоже условное, поэтому название “Бермудский треугольник” не является географическим. (Слайды 4, 9).
Треугольник Пенроуза… Эта фигура –возможно, первый опубликованный в печати невозможный объект. Она появилась в 1958 году в журнале. в статье под заголовком “Удивительные фигуры, особый вид оптических иллюзий”. Ее авторы, отец и сын Лайонелл и Роджер Пенроузы. Невозможный» треугольник, треугольник Пенроуза, увековечен в виде статуи в городе Перт (Австралия). Созданный усилиями художника Брайна МакКея и архитектора Ахмада Абаса, он был воздвигнут в парке Клайзебрук в 1999 году и теперь все проезжающие мимо могут видеть «невозможную» фигуру. (Слайды 4, 10).
Интересно! (Слайд 11).
–А теперь вернёмся к теме нашего урока.
VI. Первичное закрепление знаний.
Учебник: стр.138, № 318, 320, 321
VII. Подведение итогов урока.
Решение задачи, данной в начале урока
Оценивание работы учащихся и выставление отметок в журнал
VIII. Домашнее задание.
Глава 3, §22, № 319
Источник
