Свойства сложения для каких чисел


Базовые свойства
Главными элементами сложения являются аргументы (слагаемые). Сумма — результат увеличения значений первого и второго аргументов. На письме эта математическая операция обозначается символом +. Основными свойствами сложения в математике являются:


- Коммутативность: от изменения мест слагаемых сумма не меняется. Это правило также называется переместительным свойством сложения. В буквенном виде коммутативный закон записывается следующим образом: a + b = b + a. Чаще всего он применяется при решении простых уравнений и неравенств.
- Ассоциативность: порядок действия не влияет на результат сложения трех и более слагаемых. Называется это правило сочетательным свойством сложения. Ассоциативный закон применяется при группировке или перестановке слагаемых. Буквенная запись сочетательного закона выглядит следующим образом: a + b + c = a + (b + c).
- Дистрибутивность: 2 бинарные операции, определенные на одинаковом множестве, всегда находятся в согласованности. В математике это правило именуется распределительным свойством сложения.
- Нейтральный элемент: если к первому компоненту сложения прибавить нуль, то сумма будет равна исходному числу. В буквенном виде этот закон записывается так: a + 0 = a. Свойство нейтрального элемента является одним из старейших правил сложения в математике. Оно было сформировано во второй половине VII века в «Исправленном трактате Брахмы».
- Обратный элемент: при сложении чисел с одинаковым значением, но разными знаками сумма равна нулю. В буквенном выражении этот математический закон выглядит следующим образом: a + (- a) = 0.
Базовые свойства сложения изучаются в начальной школе со 2 класса. Процесс обучения начинается с простых заданий с двумя компонентами, представленными натуральными числами. По мере обучения увеличивается сложность задач и количество слагаемых. В школе большинство вычислений производится в десятичной системе счисления, поэтому в качестве памятки рекомендуется предоставить ученикам таблицу сложения, где представлены суммы пар чисел от 1 до 10.
Нахождение суммы многозначных чисел
Многозначными называются числа, состоящие из двух и более цифр. Для нахождения их суммы необходимо знание численных разрядов. Цифра, стоящая последней, показывает количество единиц. Далее идут десятки, сотни, тысячи, десятки тысяч, сотни тысяч и миллионы. Многозначные числа складываются столбиком. Сложить можно только одинаковые разряды.
Пример: найти сумму многозначных чисел 125 и 234. Отдельно складываются единицы, десятки и сотни: 5 + 4 = 9, 2 + 3 = 5, 1 + 2 = 3. Суммой является число 359.

Для проверки правильности вычислений нужно вычесть из суммы одно из слагаемых. Если разность равна второму слагаемому, то пример решен правильно. Проверку можно осуществить также при помощи калькулятора или иных вычислительных устройств.
Прибавление дробей и смешанных значений
Дробь — часть от целого числа, записываемая в виде x / y. Значение x называется числителем, y — знаменателем. Дробное число представляет собой операцию деления, где делимым является числитель, а делителем — знаменатель. Дробь считается правильной, если числитель не больше знаменателя.
При складывании дробей с одинаковыми знаменателями необходимо прибавлять только их числители (например, 1/5 + 3/5 = 4/5). Если значения, стоящие под знаком дроби, разные, то необходимо привести выражение к единому знаменателю:

- Найти наименьшее общее кратное для исходных знаменателей дробей.
- Определить дополнительные множители для числителей (наименьшее общее кратное поделить на знаменатели).
- Найти произведение числителей на дополнительные множители.
- Сложить получившиеся дроби с одинаковым знаменателем.
Для упрощения этой процедуры рекомендуется приобрести таблицу умножения. С ее помощью можно легко найти общий знаменатель и дополнительные множители.
Десятичной называется дробь, знаменатель которой равен 10. Она состоит из целой и дробной частей, отделенных запятой. При нахождении суммы десятичные дроби записываются столбиком. Важно, чтобы запятые находились на одном уровне. При неравном количестве разрядов с правой стороны дописываются нули. Если в результате после запятой стоит 0, то он опускается.

Смешанное число — сумма обыкновенной дроби (дробная часть) и целого числа (целая часть).
Для определения суммы чисел в смешанной записи необходимо отделить целую часть от дроби и сложить их по отдельности, применяя базовые свойства сложения. Если в результате вычислений получилась неправильная дробь, то нужно следовать следующему алгоритму действий:
- Найти произведение знаменателя и целой части смешанного числа.
- Прибавить к получившемуся числу числитель дробной части.
- Результат измерений записать в качестве числителя, а число, стоящее под знаком дроби, оставить без изменений.
В математике процесс преобразования неправильной дроби в смешанное число называется выделением целой части. Если числитель полностью делится на знаменатель, то неправильную дробь можно записать в виде целого числа.
Складывание векторов, пределов и матриц
Вектор — отрезок, имеющий длину и направление. Он является одним из основополагающих понятий линейной алгебры. В буквенном виде он записывается двумя заглавными символами латинского алфавита или одной маленькой латинской буквой. Существует два основных способа сложения векторов:
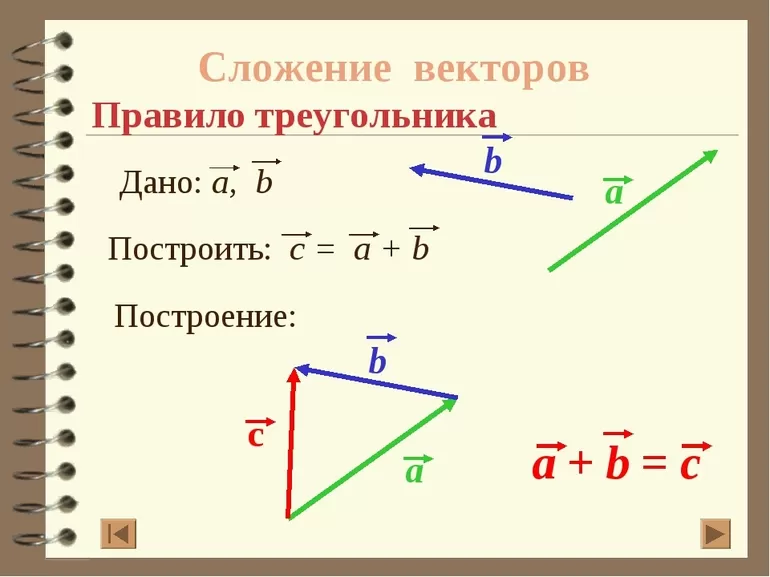
- Метод треугольников: на плоскости необходимо отметить произвольную точку и отложить от нее первый вектор. От конца первого отрезка откладывается второй. Начало первого вектора и конец второго нужно соединить. Полученный отрезок является их суммой. Этот способ используется только для нахождения суммы коллинеарных векторов, не лежащих на параллельных прямых.
- Правило параллелограмма: нужно отметить на плоскости произвольную точку и отложить от нее оба вектора. Фигура достраивается до параллелограмма. Диагональ этого многоугольника является суммой векторов.
Для нахождения суммы трех и более векторов необходимо отметить на плоскости произвольную точку и последовательно отложить от нее исходные векторы. Отрезок, соединяющий начало первого вектора и конец последнего, является суммой. При сложении важно учитывать, что результат сложения противоположно направленных векторов равен 0. Наглядно способы нахождения суммы векторов проиллюстрированы ниже.
Пределом функции является число, к которой стремится значение функции f (x) при стремлении ее аргумента к заданной точке на графике. Является одним из разделов математического анализа. Предел функции вычисляется по следующей формуле: limx →∞ f (x)= C, где C — число, к которому стремится аргумент функции. Для нахождения предела суммы необходимо сложить функции, стремящиеся к идентичным точкам на заданном графике.

Матрица — элемент высшей математики, представленный в виде таблицы прямоугольной формы. Она состоит из неограниченного количества строк и столбцов, где записываются целые, действительные, иррациональные и комплексные числа. В квадратных матрицах количество столбцов и строк совпадает. Нулевой называется таблица, где все компоненты равны 0. Матрицы нашли применение в записи алгебраических и дифференциальных уравнений.
Складывать можно только одноразмерные матрицы (число строк и столбцов совпадает). В противном случае может измениться их исходный размер. При нахождении суммы матриц каждые элементы складываются по отдельности. Нельзя сложить компоненты, находящиеся в разных строках или столбцах. В результате получится матрица с исходным размером. При сложении применяются свойства коммутативности и ассоциативности. Для складывания нулевых матриц важно знать правило нейтрального элемента.
Сложение в двоичной системе счисления
В двоичной системе счисления математические операции выполняются на электронно-вычислительных машинах. В ней применяются только две цифры: 0 и 1. Сложение в этой системе счисления выполняется в столбик. Для вычислений требуется следующая таблица:

| Условие математической операции |
| 0 + 0 = 0 |
| 0 + 1 = 1 |
| 1 + 0 = 1 |
| 1 + 1 = 10 |
Числа, записываемые в столбик, выравниваются по разделителю целой и дробной частей. Если количество разрядов не совпадает, то с правой стороны необходимо добавить нули. При складывании нескольких чисел возможен перенос через 2 и более разряда.
Для упрощения математической операции можно перевести числа из двоичной системы счисления в десятичную. Для этого над каждой цифрой исходного числа слева направо ставится степень, начиная от 0. Каждый элемент умножается на цифру 2, возведенную в соответствующую степень. Результаты вычислений суммируются. С помощью этого способа можно также переводить в восьмеричную и шестнадцатеричную системы счисления.
Источник
В учебниках часто объясняют сложение с помощью яблок и равенства 3 + 2 = 5[1]
Сложе́ние (приба́вление[2]) — одна из основных бинарных математических операций (арифметических действий) двух аргументов (слагаемых), результатом которой является новое число (сумма), получаемое увеличением значения первого аргумента на значение второго аргумента. На письме обычно обозначается с помощью знака «плюс»: .
В общем виде можно записать: , где и . То есть каждой паре элементов из множества ставится в соответствие элемент , называемый суммой и [3].
Сложение возможно только, если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип).
На множестве вещественных чисел график функции сложения имеет вид плоскости проходящей через начало координат и наклоненной к осям на 45° угловых градусов[4][5].
У сложения есть несколько важных свойств (например для ):
Коммутативность:
Ассоциативность (см. Сумма):
Дистрибутивность:
Прибавление (нулевого элемента) даёт число равное исходному:
Сложение с противоположным элементом даёт :
В качестве примера, на картинке справа запись обозначает три яблока и два яблока вместе, что в сумме дает пять яблок. Заметим, что нельзя сложить например 3 яблока и 2 груши. Таким образом, . Помимо счета яблок, сложение также может представлять объединение других физических и абстрактных величин, таких как: отрицательные числа, дробные числа, векторы, функции, и другие.
Известны различные устройства для сложения: от древних абаков до современных компьютеров, задача реализации наиболее эффективного сложения для последних является актуальной по сей день.
Формы записи и терминология
Сложение записывается с использованием символа плюса «» между слагаемыми; такая форма записи называется инфиксной нотацией. Результат записывается с использованием знака равенства «», например:
;
(«три плюс три равно шесть») ;
(«тридцать пять плюс шестьдесят четыре равно девяносто девять») .
Сложение в столбик:
5 + 12 = 17
В ряде ситуаций подразумевается сложение, но при этом символы сложения не используются:
Такая запись может вызвать путаницу, поскольку в большинстве других случаев, подобная запись означает умножение, а не сложение[8].
Свойства
Операция сложения на числовых множествах имеет следующие основные свойства:
- Сложение коммутативно — от перемены мест слагаемых сумма не меняется, так-же известно, как переместительный закон сложения:
Коммутативность:
- Сложение ассоциативно — при последовательном выполнении сложения трёх или более чисел последовательность выполнения операций не имеет значения, так-же известно, как сочетательный закон сложения:
Ассоциативность (см. Сумма):
- Сложение дистрибутивно, это — свойство согласованности двух бинарных операций, определённых на одном и том же множестве, так-же известно, как распределительный закон[9] .
Дистрибутивность: Нулевой элемент:
- Сложение с противоположным элементом даёт :
[10]
Операция сложения чисел определённых на множествах даёт число (сумму) принадлежащее этому-же множеству (операция, не выводит результат из данного множества чисел), следовательно множества замкнуты относительно операции сложения. Так же множества чисел с операциями и образуют кольца (коммутативные кольца с единицей)[11].
На языке общей алгебры вышеперечисленные свойства сложения говорят о том, что являются абелевыми группами относительно операции сложения.
Выполнение сложения
Операцию сложения можно представить, как некий “черный ящик” с двумя слагаемыми на входе и одним выходом – суммой:[12][13]
При практическом решении задачи сложения двух чисел необходимо свести её к последовательности более простых операций: “простое сложение”[источник не указан 774 дня], перенос, сравнение и др. Для этого разработаны различные методы сложения, например для чисел, дробей, векторов и др. На числовых множествах используется алгоритм поразрядного сложения[14]. При этом следует рассматривать сложение как процедуру (в отличие от операции).
Примерный алгоритм процедуры поразрядного сложения двух чисел[15]
Как видим, процедура достаточно сложная, состоит из относительно большого числа шагов и при сложении больших чисел может занять продолжительное время.
“Простое сложение” – в данном контексте обозначает операцию сложения одноразрядных чисел, которая может быть легко сведена к инкрементированию.[источник не указан 774 дня] Является гипероператором инкрементирования:
Пример пошагового сложения чисел 2 и 4 на числовой прямой.
где – последовательность операций инкрементирования, выполненная и раз.
Чтобы упростить и ускорить процесс сложения используют табличный метод “простого сложения”, для этого заранее вычисляют все комбинации сумм чисел от 0 до 9 и берут готовый результат из этой таблицы [16]:
таблица для сложения в десятичной системе счисления
| + | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
Данная процедура применима к сложению натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.
Сложение чисел
Натуральные числа
Воспользуемся определением натуральных чисел как классов эквивалентности конечных множеств. Обозначим классы эквивалентности конечных множеств порождённых биекциями, с помощью скобок: . Тогда арифметическая операция «сложение» определяется следующим образом:
где — дизъюнктное объединение множеств. Данная операция на классах введена корректно, то есть не зависит от выбора элементов классов, и совпадает с индуктивным определением.
Взаимно однозначное отображение конечного множества на отрезок можно понимать как нумерацию элементов множества . Этот процесс нумерации называют «СЧЕТОМ»[17]. Таким образом, «счет» – это установление взаимно однозначного соответствия между элементами множества и отрезком натурального ряда чисел[18].
Для сложения натуральных чисел в позиционной системе обозначения чисел применяется поразрядный алгоритм сложения. Если даны два натуральных числа и такие, что:
где: ;
– количество цифр в числе ;
– порядковый номером разряда (позиции), ;
– основание системы счисления;
множество числовых знаков (цифр), конкретной системы счисления:
,
,
;
тогда:
складывая поразрядно, получаем[коллизия переменных: c – значит две разные вещи]:
Таким образом операция сложения сводится к процедуре последовательного простого сложения одноразрядных чисел , с формированием единицы переноса при необходимости, которое производится либо табличным методом, либо инкрементированием (счетом).
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами[19]. При этом нужно пользоваться таблицей сложения, соответствующей данному основанию системы счисления.
Пример сложения натуральных чисел в двоичной, десятичной и шестнадцатеричной системах счисления, для удобства числа записываются друг под другом соответственно разрядам, единица переноса пишется сверху, недостающие разряды дополняются нулями:
Целые числа
Множество целых чисел — расширение множества натуральных чисел , получаемое добавлением отрицательных чисел [20] вида . Множество целых чисел обозначается Арифметические операции над целыми числами определяются как непрерывное продолжение соответствующих операций над натуральными числами. Отличие от натуральных чисел состоит в том, что отрицательные числа на числовой прямой направлены в противоположную сторону, это несколько меняет процедуру сложения. Необходимо учитывать взаимное направление чисел, здесь возможны несколько случаев:
Положительное и отрицательное числа на числовой прямой.
Например, рассмотрим выражение: ; так как у чисел и разные знаки, то их абсолютные величины вычитаются (из большего меньшее): , и так как абсолютная величина отрицательного числа здесь больше абсолютной величины положительного числа , то ответ будет отрицательным .
Рациональные числа
Множество рациональных чисел обозначается (от англ. quotient «частное») и может быть записано в таком виде:
Для сложения рациональных чисел в виде обыкновенных (или простых) дробей вида: , их следует преобразовать (привести) к общему (одинаковому) знаменателю. Например, взять произведение знаменателей, числители при этом умножаются на соответствующие знаменатели. Затем сложить полученные числители, а произведение знаменателей станет общим.
Если даны два рациональных числа и такие, что: (дроби не сокращаемые), тогда:
[22]
Либо можно найти наименьшее общее кратное (НОК) знаменателей. Порядок действий:
После этого знаменатели обеих дробей совпадают (равны ). В ряде простых случаев это упрощает вычисления, но в случае больших чисел расчёты значительно усложняются. Можно взять в качестве любое другое общее кратное.
Пример сложения:
Если знаменатели обеих дробей совпадают, то:
Если знаменатели кратны какому либо числу, то преобразуем только одну дробь:
Арифметическая операция «сложение» над рациональными числами относится к замкнутым операциям.
Вещественные числа
Арифметические операции над вещественными числами представимых бесконечными десятичными дробями определяются как непрерывное продолжение[23] соответствующих операций над рациональными числами.
Если даны два вещественных числа, представимые бесконечными десятичными дробями:
,
определённые соответственно фундаментальными последовательностями рациональных чисел (удовлетворяющие условию Коши), обозначенные как: и , то их суммой называют число , определённое суммой последовательностей и :
;
вещественное число , удовлетворяет следующему условию:
.
Таким образом суммой двух вещественных чисел и является такое вещественное число которое содержится между всеми суммами вида с одной стороны и всеми суммами вида с другой стороны[24].
На практике для того, чтобы сложить два числа и , необходимо заменить их с требуемой точностью приближёнными рациональными числами и . За приближенное значение суммы чисел берут сумму указанных рациональных чисел . При этом не важно, с какой стороны (по недостатку или по избытку) взятые рациональные числа приближают и . Сложение производится по алгоритму поразрядного сложения.
При сложении приближённых чисел их абсолютные погрешности складываются , абсолютная погрешность числа принимается равной половине последнего знака этого числа. Относительная погрешность суммы заключена между наибольшим и наименьшим значениями относительных погрешностей слагаемых; на практике принимается наибольшее значение .
Полученный результат округляют до первой верной значащей цифры, значащая цифра приближенного числа является верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.
Пример сложения , с точностью до 3-го знака после запятой:
График
На множестве вещественных чисел график функции сложения имеет вид плоскости проходящей через начало координат и наклоненной к осям на 45° угловых градусов. Так как , то и для этих множеств значения функции сложения будет принадлежать этой плоскости.[25]
Комплексные числа
Сложение двух комплексных чисел может быть представлено геометрически через построение параллелограмма.
Комплексные числа складываются друг с другом путём сложения действительных и мнимых частей[26]. Это значит, что:
Где: , — мнимая единица .Используя представление комплексных чисел как точек на комплексной плоскости, можно дать сложению комплексных чисел следующую геометрическую интерпретацию: суммой комплексных чисел и , представленных точками на комплексной плоскости, является точка C, полученная путём построения параллелограмма, три вершины которого находятся в точках O, A и B. Или, можно сказать, что C — это такая точка, что треугольники OAB и CBA конгруэнтны.
Аналогично для гиперкомплексных чисел (комплексных чисел n-ой размерности):
[27]
Экспоненциальная запись
В экспоненциальной записи числа записываются в виде , где — мантисса, — характеристика числа, – основание системы счисления. Для сложения двух чисел, которые записаны в экспоненциальной форме, требуется, чтобы у них были одинаковые характеристики: согласно свойству дистрибутивности.
Например:
Особый случай составляет сложение больших и малых чисел, когда одно число намного больше другого. Например , тогда соответственно и погрешности этих чисел будут несопоставимы и при выполнении сложения бо′льшая погрешность поглотит меньшую. Таким образом возможно нарушение свойства ассоциативности.
Например выражение: , если выполнить получится после округления результата , складывая далее получим , если выполнять сложение в ином порядке, тогда: . Таким образом получаются два различных результата.
Сложение произвольных чисел
При сложении чисел принадлежащих разным множествам необходимо произвести расширение числа из множества с меньшей мощностью в сторону числа из множества с большей мощностью, либо оба числа расширить до уравнивания множеств, если существует такая возможность. Например, если нужно сложить натуральное число с рациональным , то воспользовавшись тем, что натуральные числа являются подмножеством рациональных, расширяем число до рационального и складываем два рациональных числа . Аналогично, пользуясь тем, что: можно складывать числа из различных множеств между собой.[источник не указан 774 дня]
Возвращаясь к примеру с яблоками воспользуемся тем, что множество яблок и множество груш являются подмножествами множества фруктов:
можно сложить 3 яблока и 2 груши расширив оба множества до множества фруктов: фрукта_яблока фрукта_груши фруктов.[стиль]
Компьютеры
Комбинационная схема восьмиразрядного сумматора с пирамидой переносов, который складывает два двоичных восьмиразрядных числа c=a+b.
Операция сложения является базовой в Электронных цифровых Вычислительных Машинах (ЭВМ) – компьютерах. Производительность операции сложения и в особенности ограничения, связанные с механизмом переноса, влияют на общую производительность компьютера.
Основная часть компьютерного процессора – сумматор выполняет поразрядное целочисленное сложение в двоичной системе счисления, используя бинарную арифметику. Для решения задачи электронным устройством, сложение аппаратно сводится к последовательности более простых операций – «Сложение по Модулю Два», «И», «Или» и другим битовым операциям. Чтобы увеличить скорость, компьютеры вычисляют значения в разрядах параллельно, используя 32, 64, 128 и 256-битные числа. В современных компьютерах сложение целых чисел является самой быстрой операцией, в то же время оно имеет огромное влияние на общую производительность компьютера, поскольку целочисленное сложение лежит в основе всех операций с плавающей запятой, а также в таких задачах как генерация адресов во время доступа к памяти и выборка команд во время определённого порядка их выполнения.
См. также
- Сумма
- Вычитание
- Умножение
- Деление
Примечания
- ↑ Эндертон, 1977: «…выбирая два набора K и L с K = 2 и L = 3. Наборы из пальцев удобны; наборы из яблок предпочитают использовать в учебниках».
- ↑ Рудницкая В.Н., 2004, Термин используется в русскоязычных учебниках математики начальных классов, с. 110.
- ↑ Давидович, 2008, Действительные числа, ч. 1, с. 29.
- ↑ Что непосредственно вытекает из формулы плоскости , при имеем плоскость проходящую через начало координат и наклоненную к осям на 45°
- ↑ Соболев, 2012, с. 21.
- ↑ Системы счисления, 2006, с. 3.
- ↑ Девайн и соавторы, 1991, с. 263.
- ↑ Мазур, 2014, с. 161.
- ↑ Так эти свойства называются в учебниках для младших классов
- ↑ Свойства сложения, 2016, Сумма с противоположным числом, с. 1.
- ↑ Зельвенский, 2013, с. 18.
- ↑ Чёрный я́щик — термин, используемый для обозначения системы, внутреннее устройство и механизм работы которой очень сложны, неизвестны или неважны в рамках данной задачи. «Метод чёрного ящика» — метод исследования таких систем, когда вместо свойств и взаимосвязей составных частей системы, изучается реакция системы, как целого, на изменяющиеся условия.
- ↑ Эшби, 1959, с. 127-169.
- ↑ Зубарева, 2013, с. 195.
- ↑ Алгоритм сложения, с. 1.
- ↑ Истомина, 2005, с. 165.
- ↑ нумерация, Теоретические основы введения целых неотрицательных чисел, с. 7.
- ↑ Истомина2, 2009, Методика обучения математике в начальной школе, с. 71.
- ↑ Системы счисления, 2006, с. 3.
- ↑ Выгодский, 2003.
- ↑ Барсуков, 1966, с. 25.
- ↑ Гусев, 1988, с. 20.
- ↑ Поскольку на множестве вещественных чисел уже введено отношение линейного порядка, то мы можем определить топологию числовой прямой: в качестве открытых множеств возьмём всевозможные объединения интервалов вида
- ↑ Ильин, 1985, с. 46.
- ↑ График выполнен программой “3D Grapher Версия 1.2”, www.romanlab.com. Входные аргументы: x=a, y=b, z=a+b
- ↑ Конвей, 1986, с. 107.
- ↑ Александров, 1956, с. 304.
Литература
- Ильин В.А. и др. Математический анализ. Начальный курс.. — МГУ, 1985. — Т. 1. — 662 с.
- Эндертон Г. Элементы теории множеств = Elements of Set Theory. — Gulf Professional Publishing, 1977. — 279 с. — ISBN 0-12-238440-7.
- Барсуков А.Н. Алгебра. Учебник для 6-8 классов. — Просвещение, 1966. — 296 с.
- Гусев В.А., Мордкович А.Г. Математика. Справочные материалы, книга для учащихся.. — Просвещение, 1988. — 416 с.
- Истомина Н.Б. Методика обучения математике в начальной школе: Развивающее обучение.. — Ассоциация XXI век, 2005. — 272 с. — ISBN 5-89308-193-5.
- Истомина Н.Б. Методика обучения математике в начальной школе: Развивающее обучение.. — 2-е изд. — Ассоциация XXI век, 2009. — С. 71. — 288 с. — ISBN 978-5-89308-731-4.
- Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2003. — ISBN 5-17-009554-6.
- В.И. Игошин. КУРС ЧИСЛОВЫХ СИСТЕМ ДЛЯ ПЕДАГОГИЧЕСКОГО ВУЗА (рус.) : статья. — Саратовский государственный университет имени Н.Г. Чернышевского, 2010.
- Рудницкая В.Н. Математика. 1 класс. Часть 2. — Вентана Граф, 2004. — Т. 2. — 144 с. — ISBN 978-5-360-02913-7.
- Кононюк А.Е. Обобщенная теория моделирования.. — Освіта України, 2012. — Т. 2. — 548 с. — ISBN 978-966-7599-50-8.
- Под ред. Александрова А.Д., Колмогорова А.Н., Лаврентьева М.А. Математика, ее содержание, методы и значение.. — Академии наук СССР, 1956. — Т. 3. — 336 с.
- С.К. Соболев, В.Я Томашпольский. [https://hoster.bmstu.ru/~fn1/wp-content/uploads/2012/10/uchebno-metod/Surf_and_lines_ST_metod.pdf Прямые и плоскости. Методические указания к решению задач
по аналитической геометрии.]. — Москва. МГТУ им. Н.Э. Баумана., 2012. — 74 с.
- Росс Эшби У. Глава 6. Черный ящик // Введение в кибернетику = An Introduction to Cybernetics. — Издательство иностранной литературы, 1959. — С. 127-169. — 432 с.
- И. Г. Зельвенский. Группы, кольца, поля: Методические указания по дисциплине “Геометрия и алгебра”. — СПбГЭТУ, 2013. — С. 18.
- Conway, John B. Функция одной комплексной переменной = Functions of One Complex Variable I. — Springer Science, 1986. — 322 с. — ISBN 0-387-90328-3.
- Системы счисления. — Вологда: ГОУ СПО «Вологодский машиностроительный техникум», 2006. — С. 3. — 16 с.
- Mazur, Joseph. Поучительные символы: Краткая История Математических Обозначений и их Скрытых Сил = Enlightening Symbols: A Short History of Mathematical Notation and Its Hidden Powers. — Princeton University Press, 2014. — 321 с. — ISBN 1400850118.
- Devine, D.; Olson, J.; Olson, M. Элементарная математика для учителей = Elementary Mathematics for Teachers. — Wiley, 1991.
- Виленкин Н.Я. Основные свойства сложения целых чисел (рус.) : статья. — 2016. — № 1.
- Давидович Б. М., Пушкарь П. Е., Чеканов Ю. В. Математический анализ в 57-й школе. — Москва: Московского центра непрерывного математического образования (МЦНМО), 2008. — С. 29. — 177 с.
- Зубарева И.И., Мордкович А.Г. Учебник Математика 5 класс. — Москва: Мнемозина, 2013. — С. 195. — 270 с. — ISBN 978-5-346-02573-3.
Ссылки
- Теоретические основы введения целых неотрицательных чисел (рус.) 7. Проверено 19 сентября 2016.
- Сложение чисел в десятичной системе счисления. Алгоритм сложения (рус.). Проверено 26 сентября 2016.
Источник
