С каким свойством электромагнитных волн связано явление поляризации

В нашем блоге уже можно найти статьи про преломление, дисперсию и дифракцию света. Теперь пришло время поговорить о том, в чем заключается сущность поляризации света.
В самом общем смысле правильнее говорить о поляризации волн. Поляризация света, как явление, представляет собой частный случай поляризации волны. Ведь свет представляет собой электромагнитное излучение в диапазоне, воспринимаемом глазами человека.
Что такое поляризация света
Поляризация – это характеристика поперечных волн. Она описывает положение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны.
Если этой темы не было на лекциях в университете, то вы, вероятно, спросите: что это за колеблющаяся величина и какому направлению она перпендикулярна?
Как выглядит распространение света, если посмотреть на этот вопрос с точки зрения физики? Как, где и что колеблется, и куда при этом летит?
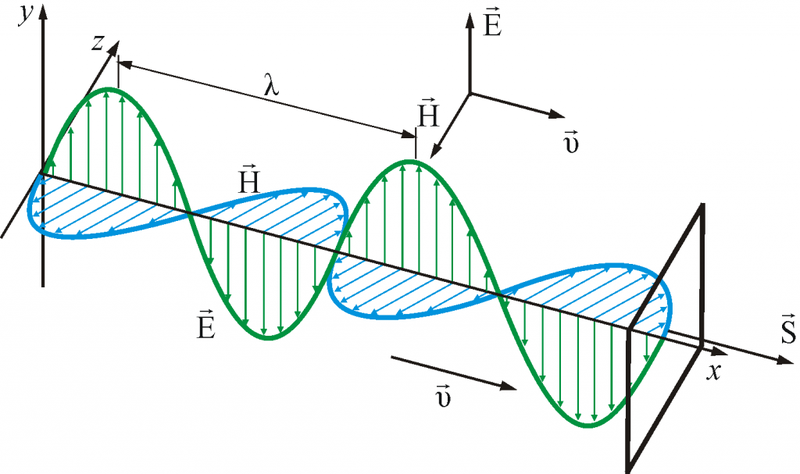 Электромагнитная волна
Электромагнитная волна
Свет – это электромагнитная волна, которая характеризуется векторами напряженности электрического поля E и вектором напряженности магнитного поля Н. Кстати, интересные факты о природе света можно узнать из нашей статьи.
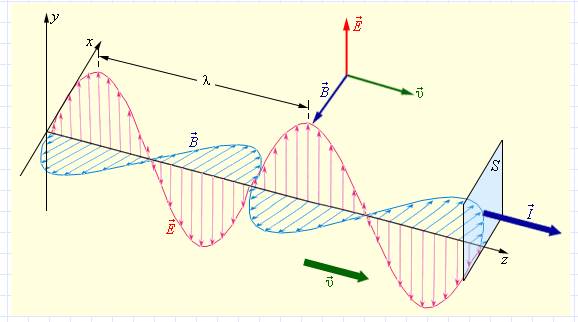
Согласно теории Максвелла, световые волны поперечны. Это значит, что векторы E и H взаимно перпендикулярны и колеблются перпендикулярно вектору скорости распространения волны.
Поляризация наблюдается только на поперечных волнах.
Для описания поляризации света достаточно знать положение только одного из векторов. Обычно для этого рассматривается вектор E.
Если направления колебаний светового вектора каким-то образом упорядочены, свет называется поляризованным.
Возьмем свет на рисунке, который приведен выше. Он, безусловно, поляризован, так как вектор E колеблется в одной плоскости.
Если же вектор E колеблется в разных плоскостях с одинаковой вероятностью, то такой свет называется естественным.
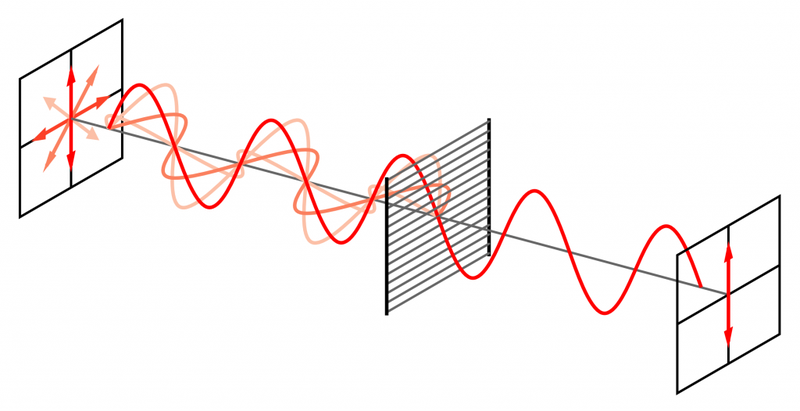 Поляризация света
Поляризация света
Поляризация света по определению – это выделение из естественного света лучей с определенной ориентацией электрического вектора.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Откуда берется поляризованный свет?
Свет, который мы видим вокруг себя, чаще всего неполяризован. Свет от лампочек, солнечный свет – это свет, в котором вектор напряженности колеблется во всех возможных направлениях. Но если вам по роду деятельности приходится весь день смотреть в ЖК-монитор, знайте: вы видите поляризованный свет.
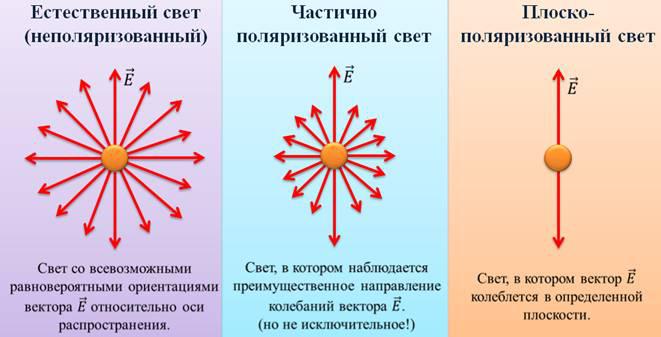 Естественный, поляризованный и частично поляризованный свет
Естественный, поляризованный и частично поляризованный свет
Чтобы наблюдать явление поляризации света, нужно пропустить естественный свет через анизотропную среду, которая называется поляризатором и «отсекает» ненужные направления колебаний, оставляя какое-то одно.
Анизотропная среда – среда, имеющая разные свойства в зависимости от направления внутри этой среды.
В качестве поляризаторов используются кристаллы. Один из природных кристаллов, часто и давно применяемых в опытах по изучению поляризации света – турмалин.
Еще один способ получения поляризованного света – отражение от диэлектрика. Когда свет падает на границу раздела двух сред, луч разделяется на отраженный и преломленный. При этом лучи являются частично поляризованными, а степень их поляризации зависит от угла падения.
 Поляризация отражением
Поляризация отражением
Связь между углом падения и степенью поляризации света выражается законом Брюстера.
Когда свет падает на границу раздела под углом, тангенс которого равняется относительному показателю преломления двух сред, отраженный луч является линейно поляризованным, а преломленный луч поляризован частично с преобладанием колебаний, лежащих в плоскости падения луча.
Линейно поляризованный свет – свет, который поляризован так, что вектор E колеблется только в одной определенной плоскости.
Практическое применение явления поляризации света
Поляризация света – не просто явление, которое интересно изучать. Оно широко применяется на практике.
Пример, с которым знакомы почти все – 3D-кинематограф. Еще один пример – поляризационные очки, в которых не видно бликов солнца на воде, а свет фар встречных машин не слепит водителя. Поляризационные фильтры применяются в фототехнике, а поляризация волн используется для передачи сигналов между антеннами космических аппаратов.
 Фото, сделанные с применением поляризационного фильтра и без него
Фото, сделанные с применением поляризационного фильтра и без него
Поляризация – не самое сложное для понимания природное явление. Хотя если копнуть глубоко и начать основательно разбираться с физическими законами, которым она подчиняется, могут возникнуть сложности.
Чтобы не терять время и преодолеть трудности максимально быстро, обратитесь за советом и помощью к нашим авторам. Мы поможем выполнить реферат, лабораторную работу, решить контрольные задания на тему “поляризация света”.
Источник
Начало XIX века для физики ознаменовалось развитием волновой теории света, которым занимались ученые Т. Юнг и О. Френель. В то время природа световых волн оставалась неизвестной. Изначально предполагалось, что свет является распространяющимися в некоторой гипотетической среде – эфире продольными волнами. Однако в процессе изучения явлений дифракции и интерференции вопрос о том, продольные или поперечные световые волны, стал второстепенен. На тот момент казалось невозможным, что свет – это поперечные волны, по той причине, что по аналогии с механическими волнами пришлось бы признать эфир твердым телом, ведь поперечные механические волны не обладают возможностью распространяться в газообразной или же жидкой среде.
Несмотря ни на что, постепенно копились свидетельствующие в пользу поперечности световых волн экспериментально полученные факты.
Определение 1
Еще в конце XVII века было обнаружено, что кристалл исландского шпата (CaCO3) обладает свойством, позволяющим ему раздваивать проходящие сквозь него лучи. Данное явление было названо двойным лучепреломлением (рис. 3.11.1).
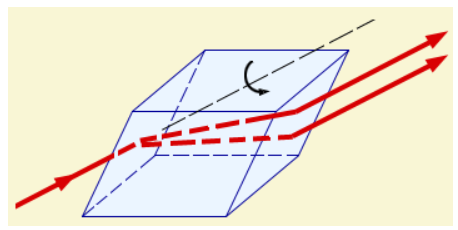
Рисунок 3.11.1. Прохождение света через кристалл исландского шпата (двойное лучепреломление). При повороте кристалла относительно направления первоначального луча оба луча, которые проходят через кристалл, тоже поворачиваются.
Поляризация света
Определение 2
Поляризация света – это явление выделения из пучка естественного света лучей с определенной ориентацией электрического вектора.
Как же получить поляризованный свет?
Определение 3
Французским инженером Э. Малюсом в 1809 году был открыт названный в его честь закон. В экспериментах Малюса свет последовательно пропускался сквозь пару одинаковых пластинок из турмалина (прозрачное кристаллическое вещество зеленоватого оттенка). Они могли поворачиваться друг относительно друга на угол φ, как это проиллюстрировано на рисунке 3.11.2.
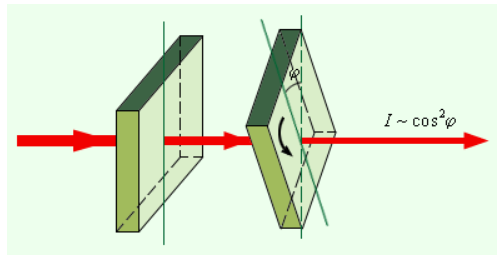
Рисунок 3.11.2. Наглядный пример закона Малюса.
Интенсивность прошедшего света оказалась прямо пропорциональной cos2 φ:
I~cos2φ.
Двойное лучепреломление точно также, как и закон Малюса не может быть объяснено с точки зрения теории продольных волн. Для продольных волн направление распространения луча представляет собой ось симметрии. В них любые направления в плоскости, нормальной, то есть перпендикулярной, лучу, равноправны.
Пример 1
В поперечной волне, к примеру, в бегущей по резиновому жгуту волне, направление колебаний и перпендикулярное ему направление не равноправны (рис. 3.11.3).
Рисунок 3.11.3. Поперечная волна в резиновом жгуте. Частицы совершают колебательные движения вдоль оси y. При повороте щели S затухнет волна.
Выходит, что асимметрия относительно направления распространения луча – это решающий признак, отличающий поперечную и продольную волны. Первым высказал догадку о поперечности световых волн Т. Юнг в 1816 году. Независимо от Юнга Френель тоже выдвинул концепцию поперечности световых волн, и даже смог обосновать ее с помощью большого количества опытов. Им была создана теория двойного лучепреломления света в кристаллах.
В середине 60-х годов XIX века Максвелл, взяв за основу совпадение известных значений скоростей распространения света и электромагнитных волн, сделал вывод о природе света. Ученый решил, что свет – это частный случай электромагнитных волн. К тому времени экспериментальным путем была подтверждена поперечность световых волн. По этой причине Максвелл предположил, что она является еще одним важным аргументом в пользу его выводов насчет электромагнитной природы света.
Пропала необходимость во введении особой среды распространения волн – эфира, который приходилось рассматривать как твердое тело. Благодаря этому электромагнитная теория света приобрела должную стройность.
В условиях электромагнитной волны вектора E→ и B→ направлены перпендикулярно друг к другу и находятся в плоскости, которая перпендикулярна направлению распространения волны плоскости. (рис. 2.6.3)

Рисунок 2.6.3. Синусоидальная (гармоническая) электромагнитная волна. Векторы E→, B→и υ→ взаимно перпендикулярны.
Определение 4
В каждом из процессов взаимодействия света с веществом электрический вектор E→ играет основную роль. По данной причине его называют световым вектором.
Виды поляризации света
Определение 5
Если при распространении электромагнитной волны световой вектор сохраняет свою ориентацию, то подобная волна носит название линейно поляризованной или плоско поляризованной. Отметим, что термин поляризации волн ввел Малюс применительно к поперечным механическим волнам.
Определение 6
Плоскость, в которой колеблется световой вектор E→, носит название плоскости колебаний (то есть плоскость yz, изображенная на рисунке 2.6.3), а плоскость, в которой совершает колебание магнитный вектор B→, является плоскостью поляризации (плоскость xz на рисунке 2.6.3).
Определение 7
В случае, когда две поляризованные в двух взаимно перпендикулярных плоскостях монохроматические волны распространяются вдоль одного и того же направления, в общем случае результатом их сложения будет эллиптически поляризованная волна (смотрите рисунок 3.11.4).
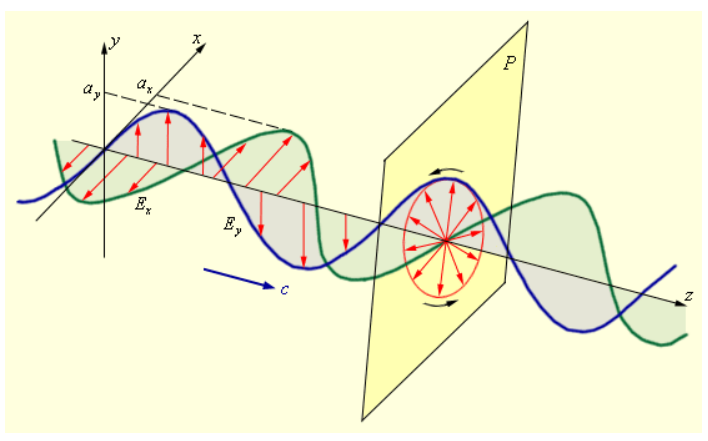
Рисунок 3.11.4. Сложение двух взаимно перпендикулярно поляризованных волн и образование эллиптически поляризованной волны.
Определение 8
В нормальной (то есть перпендикулярной) направлению распространения волны эллиптически поляризованной волне в каждой плоскости P конец результирующего вектора E→ за период светового колебания обходит некоторый эллипс, носящий название эллипса поляризации.
Его размер и форма характеризуются амплитудами ax и ay линейно поляризованных волн и фазовым сдвигом Δφ между ними.
Определение 9
Волна, обладающая круговой поляризацией (ax=ay, Δφ=±π2) представляет собой частный случай эллиптически поляризованной волны.
Данные, получаемые при просмотре рисунка 3.11.5, дают представление о пространственной структуре эллиптически поляризованной волны.
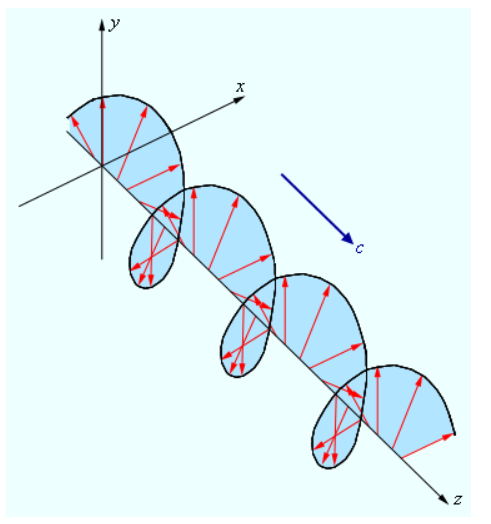
Рисунок 3.11.5. Электрическое поле в эллиптически поляризованной волне.
Линейно поляризованный свет производится лазерными источниками. В случае отражения или рассеяния свет может стать поляризованным. В частности, голубой свет от неба частично или полностью поляризован. Однако, свет, который испускают обычные источники, такие как, например, солнечный свет и излучение ламп накаливания, является неполяризованным. Свет, исходящий от подобных источников, в любой момент состоит из вкладов огромного числа независимо излучающих атомов, обладающими различной ориентацией светового вектора в волнах, которые они излучают. По этой причине в результирующей волне вектор E→ хаотично меняет свою ориентацию во времени, из-за чего в среднем все направления колебаний получаются равноправными.
Определение 10
Неполяризованный свет также называют естественным светом.
В любой момент времени вектор E→ может быть спроецирован на две взаимно перпендикулярные оси (смотри рисунок 3.11.6).
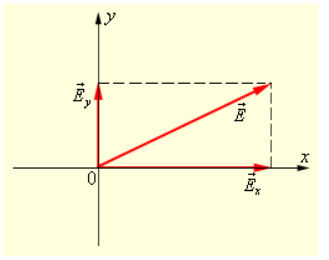
Рисунок 3.11.6. Разложение вектора E→ по осям Ох и Оу.
Это значит, что любую волну, вне зависимости от того, поляризованная она или же нет, можно представить в виде суперпозиции двух линейно поляризованных во взаимно перпендикулярных направлениях волн: E→(t)=Ex→(t)+Ey→(t). В поляризованной волне обе составляющие Ex(t) и Ey(t) когерентны, то есть разность фаз между Ex(t) и Ey(t) не претерпевает изменений, а в неполяризованной – некогерентны, значит разность фаз представляет собой случайную функцию времени.
Явление двойного лучепреломления света основывается на том, что в кристаллических веществах показатели преломления линейно поляризованных во взаимно нормальных направлениях волн, зачастую различны. По данной причине кристалл раздваивает лучи, которые проходят сквозь него так, как это показано на рисунке 3.11.1. Два луча на выходе кристалла линейно поляризованы во взаимно перпендикулярных направлениях.
Определение 11
Кристаллы, в которых происходит двойное лучепреломление, называются анизотропными.
Прибегая к разложению вектора E→ на составляющие по осям, можно объяснить закон Малюса (рис. 3.11.2).
Определение 12
У значительной части кристаллов поглощение света кардинально зависимо от направления электрического вектора в световой волне. Такое явление носит название дихроизма.
Пример 2
В частности, данным свойством обладают использованные в знакомых нам опытах Малюса пластины турмалина. При некоторой толщине пластинка турмалина практически полностью поглощает одну из взаимно перпендикулярно поляризованных волн (как, к примеру, Ex) и частично пропускает вторую волну (то есть Ey).
Определение 13
Направление колебаний электрического вектора в прошедшей волне является разрешенным направлением пластины.
Пластинка турмалина может применяться как для создания поляризационного света, то есть в качестве поляризатора, так и для анализа характера поляризации света, как анализатор.
Определение 14
В наше время часто применяются искусственные дихроичные пленки, называющиеся поляроидами.
Поляроиды пропускают практически всю волну разрешенной поляризации и не пропускают поляризованную в нормальном направлении волну. Исходя из всего вышесказанного, можно заявить, что поляроиды – это идеальные поляризационные фильтры.
Пример 3
Разберем последовательное прохождение естественного света через пару идеальных поляроидов П1 и П2 (рисунок 3.11.7), чьи разрешенные направления развернуты друг относительно друга на угол φ. Первый поляроид в приведенном тандеме занимает место поляризатора. Он преобразовывает естественный свет в линейно поляризованный. Второй поляроид применяется в качестве анализатора.
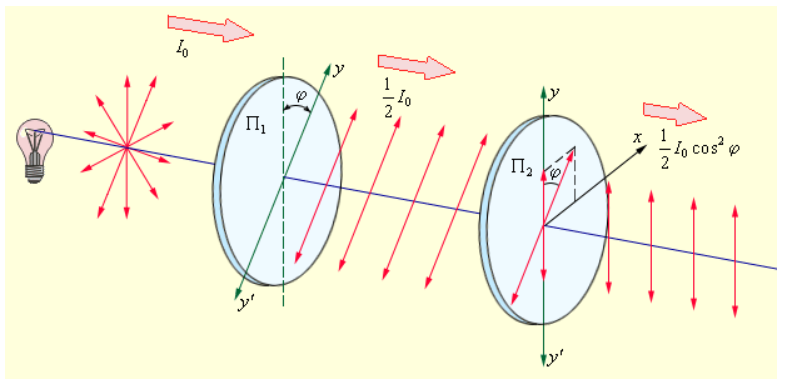
Рисунок 3.11.7. Прохождение естественного света через два идеальных поляроида. yy’представляет собой разрешенные направления поляроидов.
Обозначение амплитуды линейно поляризованной волны после прохождения света через первый поляроид в виде E0=I02 приводит к тому, что пропущенная вторым поляроидом волна приобретает амплитуду E=E0 cos φ. Таким образом, интенсивность I линейно поляризованной волны на выходе второго поляроида может быть записана в виде следующего выражения:
I=E2=E02cos2φ=12I0cos2φ.
Выходит, что в электромагнитной теории света закон Малюса находит естественное объяснение, чья основа заключается в разложении вектора E→ на его составляющие.
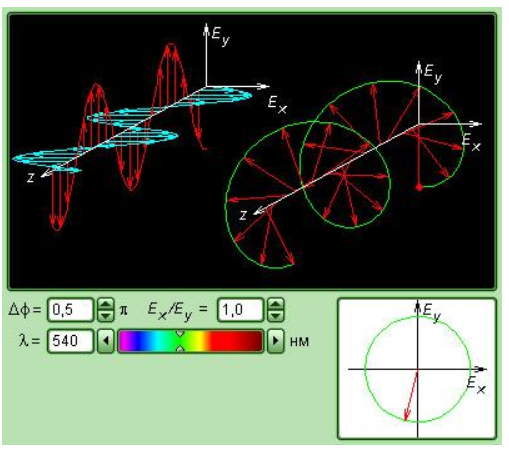
Рисунок 3.11.8. Модель поляризации света.
Рисунок 3.11.9. Модель закона Малюса.
Источник
Выше на основе уравнений Максвелла было показано, что в бегущей плоской электромагнитной волне векторы
и в каждой точке и в каждый момент времени образуют с волновым вектором правую тройку векторов. В этом заключается свойство поперечности электромагнитных волн.
Выберем ось Z системы координат вдоль волнового вектора
. Тогда у векторов и могут быть отличны от нуля только проекции на оси X и Y . Уравнения Максвелла допускают, в частности, такое решение, когда у вектора во всех точках и во все моменты времени отлична от нуля только одна проекция, например EX(Z,T). Вследствие упомянутого выше свойства поперечности, у вектора отлична от нуля только проекция на ось Y, т. е. By(Z,T). Мгновенный «снимок» такой волны, показывающий векторы и в разных точках оси Z в один момент времени приведён на рис. 1.
В таком случае говорят, что волна имеет линейную, или плоскую, поляризацию. В плоскости, перпендикулярной направлению распространения, концы векторов
и за период описывают две взаимно перпендикулярные линии, длина которых определяется удвоенной амплитудой соответственно электрической и магнитной составляющих поля. Плоскость, в которой лежит вектор напряжённости электрического поля волны и волновой вектор , называют Плоскостью Поляризации или плоскостью колебаний. Чтобы представить себе изменения электрического и магнитного полей с течением времени, можно считать, что вся система векторов на рис. 1 движется как целое вдоль оси Z со скоростью C.
Эллиптическая поляризация
В рассмотренном примере линейно поляризованной волны предполагалось, что вектор
во всех точках направлен параллельно или антипараллельно оси X (см. рис. 1). В общем случае у плоской гармонической волны, распространяющейся вдоль оси Z, отличны от нуля обе компоненты Ex и Ey, а вектор электрического поля имеет вид
Рассмотрим плоскую волну, компоненты электрического поля которой изменяются по гармоническому закону
(1)
, (2)
Где d — сдвиг фаз между колебаниями.
Найдём уравнение траектории, по которой движется конец вектора
в плоскости Z = Const. Перепишем (2) в виде
И с помощью (1) исключим из этого равенства cos (wT – Kz) и sin (wT – Kz):
(3)
Напомним, что амплитуды E10И E20 предполагаются положительными числами. Перенесём первое слагаемое правой части (3) на левую сторону, делим обе части на E20 и возводим их в квадрат.
Раскрываем скобки и приводим уравнение к виду
(4)
Соотношение (4) является уравнением конического сечения. Оно имеет форму эллипса, так как соответствующий детерминант неотрицателен, т. е.
.
Эллипс вписан в прямоугольник, стороны которого имеют длины 2E10 и 2E10 (рис. 2). Эллипс касается сторон прямоугольника в точках AA¢(±E10, ±E20cosd) и BB¢(±E10cosd, ±E20).
Итак, в общем случае при распределении плоской монохроматической световой волны конец вектора
в плоскости Z = const описывает эллипс. Аналогично ведёт себя и вектор напряжённости магнитного поля. Такая волна называется эллиптически поляризованной.
Представить себе электрическое поле такой волны при фиксированном T можно так: на поверхности прямого эллиптического цилиндра проведена винтовая линия, начала всех векторов
находятся в точках оси цилиндра, концы — на винтовой линии, причём сам вектор везде перпендикулярен оси.
Правая и левая эллиптические поляризации
Двигаясь по эллипсу в плоскости Z = const, конец вектора
может вращаться по часовой или против часовой стрелки. Для того чтобы различить эти два состояния, в оптике вводят понятия Правой поляризации (для наблюдателя, смотрящего навстречу световому лучу, вращение происходит по часовой стрелке) и Левой поляризации (вращение вектора в противоположном направлении). Покажем, что направление вращения вектора зависит от знака разности фаз d. Выберем момент времени T0, для которого wT0 – Kz =0. В этот момент, согласно формулам (1) и (2),
,
Так что
(5)
Из формул (5) видно, что в тот момент, когда конец вектора
достигает крайней правой точки своей траектории (рис. 2), имеем DE/DT < 0, если 0 < d < p, и DE/DT > 0, если – p < d < 0. Очевидно, что первый из этих случаев соответствует право поляризованной волне, а второй — лево поляризованной.
Итак, в общем случае плоская монохроматическая волна имеет правую или левую эллиптическую поляризацию. Полная характеристика эллипса поляризации даётся тремя параметрами E10, E20 и d. И, как видно из рис. 2, оси эллипса могут быть не параллельны осям OXИ OY. Однако если заданы E10, E20 и разность фаз d, относящиеся к произвольному положению осей, и если a (0 < a £ p/2) — угол, определяемый соотношением
,
То главные полуоси эллипса AИ B и угол y (0 < y £ p/2), который большая ось образует с осью Ox, находятся из формул
, (6)
Где c (-p/4 £ c £ p/4) — вспомогательный угол, определяющий форму и ориентацию эллипса колебаний, а именно:
(7)
Численное значение Tg C определяет величину отношения осей эллипса, а знак при c характеризует два варианта, которые можно использовать при описании эллипса. Из последней формулы (6) видно, что при правой эллиптической поляризации, когда sin d > 0, то угол c меняется в пределах 0 < c £ p/4, что соответствует знаку “+” в формуле (7). Соответственно для левой поляризации — знак “–”.
Параметры A, B и y можно определить на опыте, а, зная эти величины, по формулам (6) можно рассчитать амплитуды E10, E20 и разность фаз d.
Линейная и круговая поляризации
Наиболее важны два частных случая, когда эллипс поляризации вырождается либо в прямую, либо в окружность.
Согласно (1) и (2) эллипс переходит в прямую при
.
Тогда
,
И мы говорим о линейной поляризации.
На рис. 3а показаны два возможных направления поляризации в плоско поляризованной волне, соответствующие d = 0 и d = p.
Другой важный специальный случай — случай круговой поляризации волны, когда эллипс вырождается в круг. Ясно, что необходимое условие этого заключается в превращении описанного прямоугольника в квадрат, т. е.
Кроме того, одна из компонент
должна равняться нулю, когда другая достигает максимального значения. Отсюда следует, что
И уравнение (4) переходит в уравнение окружности
.
В случае правой поляризации sin d > 0, так что
,
,
Где
. (8)
В случае левой поляризации sind < 0, так что
,
,
Где
. (9)
Из формул (8) и (9) следует, что
.
Это означает, что сумма право — и лево- поляризованных волн даёт линейно поляризованную волну.
Если вместо вещественного представления воспользоваться комплексным, т. е. вместо косинусов в (1) и (2) использовать экспоненциальные функции
и ,
То
,
И из знания этого отношения сразу же можно определить характер поляризации:
А) Линейная поляризация
.
Б) Правая круговая поляризация электрической волны
,
.
В) Левая круговая поляризация
,
.
В более общем случае можно показать, что для правой эллиптической поляризации мнимая часть отношения EY/Ex положительна, тогда как для левой эллиптической поляризации она отрицательна.
На рис. 3б показана круговая поляризация, на рис. 3в эллипсы поляризации при разных значениях d.
Параметры Стокса. Сфера Пуанкаре.
Как уже отмечалось, для определения эллипса поляризации необходимы три независимые величины, например амплитуды E10, E20 и разность фаз или малая и большая оси A, B и угол y, характеризующий ориентацию эллипса. Для практических целей состояние поляризации удобно задавать некоторыми параметрами, обладающими одинаковой физической размерностью. Такие параметры были введены Стоксом, и для любой волны их можно определить из простых экспериментов.
Для плоской монохроматической волны параметрами Стокса служат четыре величины.
(10)
Лишь три из них независимы, так как справедливо тождество
(11)
Очевидно, что параметр S0 пропорционален интенсивности волны. Параметры S1, S2, S3 простым образом связаны с углом y, характеризующим ориентацию эллипса, и углом c, характеризующим эллиптичность и направление вращения. Справедливы следующие соотношения:
. (12)
Например, последнее из уравнений можно получить, используя ранее записанные соотношения:
,
,
,
;
И тригонометрические формулы
.
Следовательно,
.
Выражения (12) подсказывают простое геометрическое представление различных состояний поляризации: S1, S2, S3 можно рассматривать как декартовы координаты точки P на сфере S радиуса S0, причём 2c и 2y являются сферическими угловыми координатами этой точки (рис. 4). Каждому возможному состоянию поляризации плоской монохроматической волны заданной интенсивности (S0 = Const) соответствует одна точка на сфере S, и наоборот.
Так как угол c (или sin(2c)) положителен или отрицателен в зависимости от того, имеем ли мы дело с правой или левой поляризацией, то из последнего уравнения соотношения (12) следует, что правая поляризация представляется точками на S, лежащими выше экваториальной плоскости, а левая — точками на S, лежащими ниже этой плоскости.
Для линейно поляризованного света разность фаз равна нулю или целому, кратному p. Тогда, согласно последнему уравнению соотношений (10), параметр Стокса S3 равен нулю, так что линейная поляризация представляется точками на экваториальной плоскости.
Правая круговая поляризация представляется северным полюсом (E10 = E20 = E00, S1 = 0, d = p/2, S2 = 0, S3 = S0), а левая поляризация — южным полюсом (E10 = E20 = E00, S1 = 0, d = – p/2, S2 = 0,
). Такое геометрическое представление различных состояний поляризации точками на сфере было предложено Пуанкаре. Оно чрезвычайно полезно в кристаллооптике для определения влияния материальных сред на состояние поляризации проходящего через них света. Сфера S называется сферой Пуанкаре.
В плоской монохроматической волне напряженность электрического поля
(а также и магнитного поля ) есть Регулярная Функция Координат И Времени. Такая волна называется полностью поляризованной или просто поляризованной. Мы дали исчерпывающее представление о состояниях поляризации такой волны. Показали, что в общем случае такая волна поляризована эллиптически, а характеристики эллипса поляризации определяются амплитудами и фазами ортогональных компонент светового поля EX и EY.
Немонохроматический свет. Матрица когерентности.
Конечная ширина, или как принято говорить Апертура (от лат. Apertura— отверстие) реальных световых пучков, определяемая размерами линз, зеркал или оправ оптических деталей, и немонохроматичность света приводят к отличиям от этой идеальной картины. Если свет лазера бывает близок по своей структуре к поляризованной волне, то поляризация излучения не лазерного источника света испытывает быстрые хаотические изменения во времени.
Поле немонохроматической световой волны естественно рассматривать как случайный процесс. Для такой волны направление вектора
в плоскости фронта волны случайным образом меняется с течением времени. Если при этом все направления оказываются равновероятными, то свет называется неполяризованным или естественно поляризованным. Таков, например, солнечный свет или свет лампы накаливания. Если же существует некоторое преимущественное направление вектора , то говорят, что свет частично поляризован.
Световое поле плоской немонохроматической волны со средней частотой v, распространяющейся вдоль оси Z, можно представить в виде
,
Где
.
Амплитуды ортогональных компонент поля E0x и E0y могут быть комплексными, и, рассматривая их как случайные функции времени, вводится матрица когерентности световой волны
Где угловые скобки обозначают усреднение по времени. Элементы этой матрицы могут быть измерены экспериментально. Матрица когерентности характеризует поляризацию плоской немонохроматической световой волны.
Источник
