При каком условии резонансные свойства колебательной
Резонансные явления наблюдаются в колебательных системах, когда частота собственных колебаний элементов системы совпадает с частотой внешних (вынужденных) колебательных процессов. Данное утверждение справедливо и для цепей с циркулирующим переменным током. В таких электрических цепях при наличии определённых условий возникает резонанс напряжений, что влияет на параметры тока. Явление резонанса в электротехнике может быть полезным или вредным, в зависимости от ситуации, в которой происходит процесс.
Описание явления
Если в некой электрической цепи (см. рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.
 Рис. 1. Резонанс в электрической цепи
Рис. 1. Резонанс в электрической цепи
Давайте рассмотрим на этом примере, какие явления будут происходить при подключении генератора переменного тока к контактам схемы. Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.
Индуктивный элемент вызывает сдвиг фаз, характеризующийся отставанием тока от напряжения на ¼ периода. Под действием конденсатора ток, наоборот, на ¼ периода опережает напряжение.
Другими словами, действие индуктивности противоположно действию на сдвиг фаз ёмкостного сопротивления. То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.
Формула
Общее реактивное сопротивление рассматриваемых нами элементов равно сумме сопротивлений каждого из них. С учётом противоположности действий можно записать: Xобщ = XL — Xc , где XL = ωL — индуктивное реактивное сопротивление, выражение Xc = 1/ωC — это ёмкостное реактивное сопротивление.
На рисунке 2 изображены графики зависимости полного сопротивления цепи и связанной с ним силы тока, от реактивного сопротивления индуктивного элемента. Обратите внимание на то, как падает полное сопротивление при уменьшении реактивной сопротивляемости RL (график б) и как при этом возрастает ток (график в).
 Рис. 2. Графики зависимости параметров тока от падения реактивного сопротивления
Рис. 2. Графики зависимости параметров тока от падения реактивного сопротивления
Электрические цепи, состоящие из последовательно соединённых конденсаторов, пассивный резисторов и катушек индуктивности называют последовательными резонансными (колебательными) контурами (см. рис. 2). Существуют также параллельные контуры, в которых R, L, C элементы подключены параллельно (рис. 3).
 Рис. 3. Последовательный колебательный контур
Рис. 3. Последовательный колебательный контур Рис. 4. Параллельный колебательный контур
Рис. 4. Параллельный колебательный контур
В режиме резонанса мощность источника питания будет рассеиваться только на активных сопротивлениях (в том числе на активном сопротивлении катушки). Для резонансных контуров характерны потери только активной мощности, которая израсходуется на поддержание колебательного процесса. Реактивная мощность на L C — элементах при этом не расходуется. Ток в резонансном режиме принимает максимальное значение:

Величину Q принято называть термином «Добротность контура». Данный параметр показывает, во сколько раз напряжение, возникшее на контактах реактивных элементов, превышает входное напряжение U электрической сети. Для описания соотношения выходного и входного напряжений часто применяют коэффициент K. При резонансе:
K = Uвых / Uвх = UC0 / U = Q
Формулировка
На основании вышеописанных явлений, сформулируем определение резонансного напряжения: «Если общее падение напряжения на ёмкостно-индуктивных элементах равно нулю, а амплитуда тока – максимальна, то такое особое состояние системы называется резонансом напряжений». Для лучшего понимания явления, немного перефразируем определение: резонансом напряжений является состояние, когда напряжение на CL — цепочке больше чем на входе электрической цепи.
Описанное явление довольно распространено в электротехнике. Иногда с ним борются, а иногда специально создают условия для образования резонанса. Основными характеристиками всякого резонансного контура являются параметры добротности и частоты [ 1 ].
В случае, если XL = Xc – справедливо равенство: ωL = 1/ωC , отсюда получаем:

Если ω = ω0 – возникает резонанс напряжений. Частоты совпадают в том случае, когда индуктивное сопротивление сравняется с ёмкостным сопротивлением конденсатора. В таких случаях в цепи будет действовать только активное сопротивление R. Наличие реактивных элементов в схеме приводит к увеличению полного сопротивления цепи (Z):
![]()
где R – общее активное сопротивление.
Учитывая, что по закону Ома U = I/Z, можно утверждать, что общее напряжение в цепи зависит, в том числе, и от слагаемых индуктивного и ёмкостного сопротивлений.
Если бы в рассматриваемой схеме (рис. 1) отсутствовало активное сопротивление R, то значение полного сопротивления Z стремилось бы к 0. Следовательно, напряжение на реактивных элементах при этом возрастает до критического уровня.
Поскольку XL и Xc зависят от частоты входного напряжения, то для возникновения резонанса следует подобрать соответствующую частоту сети, или изменять параметры катушки, либо конденсатора до тех пор, пока резонансные частоты не совпадут. Любое нарушение условий резонанса немедленно приводит к выходу системы из резонансного режима с последующим падением напряжения.
Условия наступления
Резонансные явления наступают только при наличии следующих условий:
- Наличие минимального активного сопротивления на участке электрической цепи.
- Равенство реактивных сопротивлений, возникших на цепочке LC.
- Совпадение входной частоты источника питания с резонансной частотой колебательного контура.
При резонансе в контуре напряжения на его элементах могут повышаться на порядок и больше.
Примеры применения на практике
Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.
В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.
Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.
Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.
Конденсаторы и различные катушки индуктивности (рис. 5) входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.
 Катушки индуктивности
Катушки индуктивности
Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.
Наряду с полезными свойствами резонансных явлений, в практической электротехнике часто возникают ситуации, когда резонанс напряжений приносит вред. В основном это связано с нежелательным повышением параметров тока на участках цепей. Примером могут служить опасное резонансные явления в кабельных линиях без нагрузки, что может привести к пробоям изоляции. Чтобы этого не случилось, на концевых участках таких линий устанавливают балластные нагрузочные элементы.
Источник
Глава 4. Электромагнитные колебания
При изучении вынужденных механических колебаний мы ознакомились с явлением резонанса. Резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой изменения внешней силы. Если трение мало, то амплитуда установившихся вынужденных колебаний при резонансе резко увеличивается. Совпадение вида уравнений для описания механических и электромагнитных колебаний позволяет сделать заключение о возможности резонанса также и в электрической цепи, если эта цепь представляет собой колебательный контур, обладающий определенной собственной частотой колебаний.
При механических колебаниях резонанс выражен отчетливо при малых значениях коэффициента трения μ. В электрической цепи роль коэффициента трения выполняет ее активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника (проводник нагревается). Поэтому резонанс в электрическом колебательном контуре должен быть выражен отчетливо при малом активном сопротивлении R.
Мы с вами уже знаем, что если активное сопротивление мало, то собственная циклическая частота колебаний в контуре определяется формулой
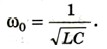
Сила тока при вынужденных колебаниях должна достигать максимальных значений, когда частота переменного напряжения, приложенного к контуру, равна собственной частоте колебательного контура:

Резонансом в электрическом колебательном контуре называется явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
Амплитуда силы тока при резонансе. Как и в случае механического резонанса, при резонансе в колебательном контуре создаются оптимальные условия для поступления энергии от внешнего источника в контур. Мощность в контуре максимальна в том случае, когда сила тока совпадает по фазе с напряжением. Здесь наблюдается полная аналогия с механическими колебаниями: при резонансе в механической колебательной системе внешняя сила (аналог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).
Не сразу после включения внешнего переменного напряжения в цепи устанавливается резонансное значение силы тока. Амплитуда колебаний силы тока нарастает постепенно — до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:
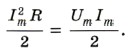
Упростив это уравнение, можно записать:
ImR = Um (4.37)
Отсюда амплитуда установившихся колебаний силы тока при резонансе определяется уравнением


При R → 0 резонансное значение силы тока неограниченно возрастает: (Im)рез → ∞. Наоборот, с увеличением R максимальное значение силы тока уменьшается, и при больших R говорить о резонансе уже не имеет смысла. Зависимость амплитуды силы тока от частоты при различных сопротивлениях (R1 < R2 < R3) показана на рисунке 4.19.
Одновременно с увеличением силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности. Эти напряжения при малом активном сопротивлении во много раз превышают внешнее напряжение.
Использование резонанса в радиосвязи. Явление электрического резонанса широко используется при осуществлении радиосвязи. Радиоволны от различных передающих станций возбуждают в антенне радиоприемника переменные токи различных частот, так как каждая передающая радиостанция работает на своей частоте. С антенной индуктивно связан колебательный контур (рис. 4.20). Вследствие электромагнитной индукции в контурной катушке возникают переменные ЭДС соответствующих частот и вынужденные колебания силы тока тех же частот. Но только при резонансе колебания силы тока в контуре и напряжения в нем будут значительными, т. е. из колебаний различных частот, возбуждаемых в антенне, контур выделяет только те, частота которых равна его собственной частоте. Настройка контура на нужную частоту ω0 обычно осуществляется путем изменения емкости конденсатора. В этом обычно состоит настройка радиоприемника на определенную радиостанцию.

Необходимость учета возможности резонанса в электрической цепи. В некоторых случаях резонанс в электрической цепи может принести большой вред. Если цепь не рассчитана на работу в условиях резонанса, то его возникновение может привести к аварии.
Чрезмерно большие токи могут перегреть провода. Большие напряжения приводят к пробою изоляции.
Такого рода аварии нередко случались еще сравнительно недавно, когда плохо представляли себе законы электрических колебаний и не умели правильно рассчитывать электрические цепи.
При вынужденных электромагнитных колебаниях возможен резонанс — резкое возрастание амплитуды колебаний силы тока и напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебаний. На явлении резонанса основана вся радиосвязь.
Вопросы к параграфу
1. Может ли амплитуда силы тока при резонансе превысить силу постоянного тока в цепи с таким же активным сопротивлением и постоянным напряжением, равным амплитуде переменного напряжения?
2. Чему равна разность фаз между колебаниями силы тока и напряжения при резонансе?
3. При каком условии резонансные свойства контура выражены наиболее отчетливо?
Источник
Глава 3. Механические колебания
Если колебательная система находится под действием внешней периодической силы, то может наступить резонанс и связанное с ним резкое увеличение амплитуды колебаний.
Любое упругое тело, будь то мост, станина машины, ее вал, корпус корабля, представляет собой колебательную систему и характеризуется собственными частотами колебаний. При работе двигателей нередко возникают периодические усилия, связанные с движением частей двигателя (например, поршней) или с недостаточно точной центровкой их вращающихся деталей (например, валов). Если частота этих периодических усилий совпадает с частотой свободных колебаний системы, то возникает резонанс. Амплитуда колебаний может возрасти настолько, что возможна поломка машин, хотя напряжение в материале и не превышает предела прочности при статических нагрузках. Дело в том, что железо, сталь и другие материалы при переменных нагрузках со временем теряют прочность, после чего внезапно разрушаются.
Во всех этих случаях принимаются специальные меры, чтобы не допустить наступления резонанса или ослабить его действие. Для этого увеличивают трение в системе или же добиваются, чтобы собственные частоты колебаний не совпадали с частотой внешней силы. Известны случаи, когда приходилось перестраивать океанские лайнеры, чтобы уменьшить вибрацию.
При переходе через мост воинским частям запрещается идти в ногу. Строевой шаг приводит к периодическому воздействию на мост. Если случайно частота этого воздействия совпадет с собственной частотой колебаний моста, то он может разрушиться.
Мы приводили примеры вредных последствий резонанса. Но есть и полезные.
С важными применениями резонанса мы ознакомимся в дальнейшем.
Вопросы к параграфу
1. Два маятника представляют собой шарики одинакового радиуса, подвешенные на нитях равной длины. Массы шариков различны. Колебания какого из маятников прекратятся быстрее: легкого или тяжелого?
2. Приходилось ли вам наблюдать явление резонанса дома или на улице?
3. Для того чтобы удержать открытую дверь в вестибюле метро (дверь открывается в обе стороны и возвращается в положение равновесия пружинами), нужно приложить к ручке двери силу около 50 Н. Можно ли открыть дверь, приложив к ручке силу 0,005 Н? (Трением в петлях двери пренебречь.)
4. При каком условии резонансные свойства колебательной системы проявляются отчетливо?
* * *
Итак, мы ознакомились с механическими колебаниями. Обратим внимание на одну общую для всех колебаний особенность, отличающую их от других видов механического движения.
Как правило, при рассмотрении механического движения тела (например, движения космического корабля или планеты под действием сил всемирного тяготения) нужно бывает определить положение тела и его скорости в любой момент времени. Но при изучении периодических колебательных процессов особый интерес представляют общие признаки, характеризующие повторяемость в движении, а не положение и скорость колеблющегося тела в любой момент времени. Важно знать амплитуду, период и фазу колебаний, т. е. величины, характеризующие процесс в целом. При вынужденных колебаниях надо знать отношение частоты вынуждающей силы ω и частоты свободных колебаний (ω0. Именно оно определяет амплитуду и фазу колебаний.
Источник
Глава 3. Механические колебания
Если колебательная система находится под действием внешней периодической силы, то может наступить резонанс и связанное с ним резкое увеличение амплитуды колебаний.
Любое упругое тело, будь то мост, станина машины, ее вал, корпус корабля, представляет собой колебательную систему и характеризуется собственными частотами колебаний. При работе двигателей нередко возникают периодические усилия, связанные с движением частей двигателя (например, поршней) или с недостаточно точной центровкой их вращающихся деталей (например, валов). Если частота этих периодических усилий совпадает с частотой свободных колебаний системы, то возникает резонанс. Амплитуда колебаний может возрасти настолько, что возможна поломка машин, хотя напряжение в материале и не превышает предела прочности при статических нагрузках. Дело в том, что железо, сталь и другие материалы при переменных нагрузках со временем теряют прочность, после чего внезапно разрушаются.
Во всех этих случаях принимаются специальные меры, чтобы не допустить наступления резонанса или ослабить его действие. Для этого увеличивают трение в системе или же добиваются, чтобы собственные частоты колебаний не совпадали с частотой внешней силы. Известны случаи, когда приходилось перестраивать океанские лайнеры, чтобы уменьшить вибрацию.
При переходе через мост воинским частям запрещается идти в ногу. Строевой шаг приводит к периодическому воздействию на мост. Если случайно частота этого воздействия совпадет с собственной частотой колебаний моста, то он может разрушиться.
Мы приводили примеры вредных последствий резонанса. Но есть и полезные.
С важными применениями резонанса мы ознакомимся в дальнейшем.
Вопросы к параграфу
1. Два маятника представляют собой шарики одинакового радиуса, подвешенные на нитях равной длины. Массы шариков различны. Колебания какого из маятников прекратятся быстрее: легкого или тяжелого?
2. Приходилось ли вам наблюдать явление резонанса дома или на улице?
3. Для того чтобы удержать открытую дверь в вестибюле метро (дверь открывается в обе стороны и возвращается в положение равновесия пружинами), нужно приложить к ручке двери силу около 50 Н. Можно ли открыть дверь, приложив к ручке силу 0,005 Н? (Трением в петлях двери пренебречь.)
4. При каком условии резонансные свойства колебательной системы проявляются отчетливо?
* * *
Итак, мы ознакомились с механическими колебаниями. Обратим внимание на одну общую для всех колебаний особенность, отличающую их от других видов механического движения.
Как правило, при рассмотрении механического движения тела (например, движения космического корабля или планеты под действием сил всемирного тяготения) нужно бывает определить положение тела и его скорости в любой момент времени. Но при изучении периодических колебательных процессов особый интерес представляют общие признаки, характеризующие повторяемость в движении, а не положение и скорость колеблющегося тела в любой момент времени. Важно знать амплитуду, период и фазу колебаний, т. е. величины, характеризующие процесс в целом. При вынужденных колебаниях надо знать отношение частоты вынуждающей силы ω и частоты свободных колебаний (ω0. Именно оно определяет амплитуду и фазу колебаний.
Примеры решения задач
Источник
