При какой температуре в 1 см3 газа содержится
Задача 62.
Вычислить массу: а) 2л Н2 при 150С и давлении 100,7кПа (755мм рт. ст.); 6) 1м3 N2 при 10°С и давлении 102,9 кПа (772мм рт. ст.); в) 0,5м3 Cl2 при 20°С и давлении 99,9 кПа (749,3мм рт. ст.).
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где P и V – давление и объём газа при температуре T; P0 (101,325кПа) и V0 – давление и объём газа при нормальных условиях; T0 (273К) – абсолютная температура. Преобразуя уравнение, получим выражение для расчета объёма газов при нормальных условиях:
Рассчитаем массу каждого газа, учитывая, что мольный объём газа равен 22,4л и, зная молекулярную массу газов, получим:
Ответ: а) 0,168г; б) 1.23кг; в) 1,456кг.
Задача 63.
Определить объем, занимаемый 0,07кг N2 при 21°С и давлении 142 кПа (106 мм рт. ст.).
Решение:
Зная мольный объём и мольную массу азота (28г/моль), находим объём, который будет занимать 0,07кг (70г) азота при нормальных условиях:
Затем приведём полученный объём к температуре Т = 21оС (294К) и Р = 142кПа, используя выражение, объединяющее законы Гей-Люссака и Бойля-Мариотта:
где P и V – давление и объём газа при температуре T; P0 (101,325кПа) и V0 – давление и объём газа при нормальных условиях; (273 К) – абсолютная температура. Преобразуя уравнение, получим выражение для расчета объёма газа при заданной температуре
Ответ: 43л.
Задача 64.
Бертолетова соль при нагревании разлагается с образованием КСI и О2. Сколько литров кислорода при 0°С и давлении 101,3 кПа можно получить из 1 моля КСIО3?
Решение:
Уравнение реакции термического разложения бертолетовой соли имеет вид:
Из уравнения реакции следует, что из двух молей бертолетовой соли образуется три моля кислорода, т.е. из одного моля соли образуется полтора моля кислорода (2:3 = 1:х; x = 1.3/2 = 1,5моль).
Объём кислорода при нормальных условиях (T0 =00С и P0 =101.325кПа) можно рассчитать по формуле:
V(B) – объём газа, л;
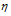(B) – количество газа, моль;
V(M) – мольный объём, 22,4л.
Тогда
V(кислорода) = 1,5 . 22,4 = 33,6л.
Ответ: 33,6л.
Задача 65.
Сколько молей содержится в 1м3 любого газа при нормальных условиях?
Решение:
Зная, что один моль любого газа при нормальных условиях (Т0 =00С и Р0 =101.325 кПа) занимает 22,4л, рассчитаем количество молей газа в 1м3 (1000 л) из пропорции:
Ответ: 44,64моль.
Задача 66.
Чему равно атмосферное давление на вершине Казбека, если при 0°С масса 1л взятого там воздуха равна 700 мг?
Решение:
Мольная масса воздуха равна 29 г/моль. Нормальными условиями для газов являются температура 00С и давление 101,325 кПа (760 мм рт ст.). Масса одного литра воздуха при нормальных условиях равна 1296,64 мг:
Теперь рассчитаем атмосферное давление на вершине Казбека из пропорции:
Ответ: 54,7к Па (410,3 мм рт. ст.).
Задача 67.
При взаимодействии одного объема СО и одного объема Сl2 образуется один объем фосгена. Установить формулу фосгена.
Решение:
По условию задачи выходит, что из молекулы угарного газа и одной молекулы хлора образуется одна молекула фосгена. Так как молекула угарного газа СО состоит из одного атома углерода и одного атома кислорода, а молекула хлора Cl2 состоит из двух атомов хлора, то, следовательно, молекула фосгена будет состоять из одного атома углерода, одного атома кислорода и двух атомов хлора. Тогда формула фосгена будет иметь вид: CCl2O.
Уравнение реакции будет иметь вид:
СО + Cl2 —> ССl2O.
Ответ: ССl2O.
Задача 68.
Какой объем СО2 получается при сгорании 2л бутана? Объемы обоих газов измерены при одинаковых условиях.
Решение:
Уравнение реакции горения бутана имеет вид:
2С4Н10 + 13О2 = 8СО2 + 10Н2О
Из уравнения реакции следует, что при сгорании одного моля бутана образуется четыре моля углекислого газа. Известно, что при одинаковых условиях одинаковое количество газов занимают одинаковый объём. Один моль любого газа при нормальных условиях занимает объём в 22,4 л.
Исходя, из этих утверждений рассчитаем объём выделившегося углекислого газа при сгорании 2 л бутана, составив пропорцию:
Ответ: 8л.
Задача 69.
В замкнутом сосуде при 120°С и давлении 600 кПа находится смесь, состоящая из трех объемов О2 и одного объема СН4. Каково будет давление в сосуде, если взорвать смесь и привести содержимое сосуда к первоначальной температуре?
Решение:
Уравнение реакции имеет вид:
CH4 + 2O2 —-> CO2 + 2H2O
Из уравнения реакции следует, что из одной молекулы метана и двух молекул кислорода образуются одна молекула углекислого газа и две молекулы воды, т. е. реакция протекает без изменения объёма. Начальный объём системы состоял из одного объёма метана и трёх объёмов кислорода, после реакции в системе остался один объём не прореагировавшего кислорода и три объёма продуктов реакции (один объём метана и два объёма паров воды). Поскольку реакция протекает без изменения объёма, а по окончании реакции содержимое сосуда приводится к первоначальной температуре, а общее число молекул газов не изменилось, то давление в системе останется прежним, т. е. 600 кПа.
Ответ: не изменится.
Задача 70. После взрыва 0,020 л смеси водорода с кислородом осталось 0,0032 л кислорода. Выразить в процентах по объему первоначальный состав смеси.
Решение:
Находим объём газов, вступивших в реакцию:
0,020 – 0,0032 = 0,0168 л.
Уравнение реакции горения водорода имеет вид:
2Н2 + О2 = 2Н2О
При взаимодействии водорода с кислородом из двух молекул водорода и одной молекулы кислорода получаются две молекулы воды, следовательно, из трёх молекул образовавшихся газов одна молекула будет принадлежать кислороду. Таким образом, объём кислорода, вступившего в реакцию, будет составлять одну треть объёма смеси газов – продуктов ре-акции. Отсюда количество кислорода, вступившего в реакцию, составляет 0,00565 л (0 0168/3 = 0,0056).
Следовательно, общее количество кислорода до реакции составляло 0,0088л (0,0056 + 0,0032 = 0,0088).
Тогда содержимое водорода до реакции составляло 0,0112л (0,02 – 0,0088 = 0.0112).
Рассчитаем в процентах первоначальный состав газовой смеси:
Ответ: 56%Н2; 44%О2.
Источник
Ñîðîêèí Â.Â., Çàãîðñêèé Â.Â., Ñâèòàíüêî
È.Â.Çàäà÷è õèìè÷åñêèõ îëèìïèàä.
1.2. Ãàçîâûå çàêîíû
Çàâèñèìîñòü ìåæäó äàâëåíèåì è îáúåìîì
èäåàëüíîãî ãàçà ïðè ïîñòîÿííîé òåìïåðàòóðå
ïîêàçàíà íà ðèñ. 1.
Äàâëåíèå è îáúåì îáðàçöà ãàçà îáðàòíî
ïðîïîðöèîíàëüíû, ò. å. èõ ïðîèçâåäåíèÿ ÿâëÿþòñÿ
ïîñòîÿííîé âåëè÷èíîé: pV = const. Ýòî ñîîòíîøåíèå
ìîæåò áûòü çàïèñàíî â áîëåå óäîáíîì äëÿ ðåøåíèÿ
çàäà÷ âèäå:
p1V1 = p2V2 (çàêîí
Áîéëÿ-Ìàðèîòòà).
Ïðåäñòàâèì ñåáå, ÷òî 50 ë ãàçà (V1), íàõîäÿùåãîñÿ
ïîä äàâëåíèåì 2 àòì (p1), ñæàëè äî îáúåìà 25 ë (V2),
òîãäà åãî íîâîå äàâëåíèå áóäåò ðàâíî:
Çàâèñèìîñòü ñâîéñòâ èäåàëüíûõ ãàçîâ îò
òåìïåðàòóðû îïðåäåëÿåòñÿ çàêîíîì Ãåé-Ëþññàêà:
îáúåì ãàçà ïðÿìî ïðîïîðöèîíàëåí åãî àáñîëþòíîé
òåìïåðàòóðå (ïðè ïîñòîÿííîé ìàññå: V = kT, ãäå k
– êîýôôèöèåíò ïðîïîðöèîíàëüíîñòè). Ýòî
ñîîòíîøåíèå çàïèñûâàåòñÿ îáû÷íî â áîëåå óäîáíîé
ôîðìå äëÿ ðåøåíèÿ çàäà÷:
Íàïðèìåð, åñëè 100 ë ãàçà, íàõîäÿùåãîñÿ ïðè
òåìïåðàòóðå 300Ê, íàãðåâàþò äî 400Ê, íå ìåíÿÿ
äàâëåíèÿ, òî ïðè áîëåå âûñîêîé òåìïåðàòóðå íîâûé
îáúåì ãàçà áóäåò ðàâåí
Çàïèñü îáúåäèíåííîãî ãàçîâîãî çàêîíà pV/T= = const
ìîæåò áûòü ïðåîáðàçîâàíà â óðàâíåíèå
Ìåíäåëååâà-Êëàïåéðîíà:
ãäå R – óíèâåðñàëüíàÿ ãàçîâàÿ ïîñòîÿííàÿ, a – ÷èñëî ìîëåé
ãàçà.
Óðàâíåíèå Ìåíäåëååâà-Êëàïåéðîíà ïîçâîëÿåò
ïðîâîäèòü ñàìûå ðàçíîîáðàçíûå âû÷èñëåíèÿ.
Íàïðèìåð, ìîæíî îïðåäåëèòü ÷èñëî ìîëåé ãàçà ïðè
äàâëåíèè 3 àòì è òåìïåðàòóðå 400Ê, çàíèìàþùèõ îáúåì
70 ë:
Îäíî èç ñëåäñòâèé îáúåäèíåííîãî ãàçîâîãî
çàêîíà: â ðàâíûõ îáúåìàõ ðàçëè÷íûõ ãàçîâ ïðè
îäèíàêîâîé òåìïåðàòóðå è äàâëåíèè ñîäåðæèòñÿ
îäèíàêîâîå ÷èñëî ìîëåêóë. Ýòî çàêîí Àâîãàäðî.
Èç çàêîíà Àâîãàäðî â ñâîþ î÷åðåäü âûòåêàåò
òàêæå âàæíîå ñëåäñòâèå: ìàññû äâóõ îäèíàêîâûõ
îáúåìîâ ðàçëè÷íûõ ãàçîâ (åñòåñòâåííî, ïðè
îäèíàêîâûõ äàâëåíèè è òåìïåðàòóðå) îòíîñÿòñÿ êàê
èõ ìîëåêóëÿðíûå ìàññû:
m1/m2 = M1/M2
(m1è m2 – ìàññû äâóõ ãàçîâ);
M1IM2ïðåäñòàâëÿåò ñîáîé
îòíîñèòåëüíóþ ïëîòíîñòü.
Çàêîí Àâîãàäðî ïðèìåíèì òîëüêî ê èäåàëüíûì
ãàçàì. Ïðè íîðìàëüíûõ óñëîâèÿõ òðóäíî ñæèìàåìûå
ãàçû (âîäîðîä, ãåëèé, àçîò, íåîí, àðãîí) ìîæíî
ñ÷èòàòü èäåàëüíûìè. Ó îêñèäà óãëåðîäà (IV),
àììèàêà, îêñèäà ñåðû (IV) îòêëîíåíèÿ îò
èäåàëüíîñòè íàáëþäàþòñÿ óæå ïðè íîðìàëüíûõ
óñëîâèÿõ è âîçðàñòàþò ñ ðîñòîì äàâëåíèÿ è
ïîíèæåíèåì òåìïåðàòóðû.
Ïðèìåð 1. Óãëåêèñëûé ãàç îáúåìîì 1 ë ïðè
íîðìàëüíûõ óñëîâèÿõ èìååò ìàññó 1,977 ã. Êàêîé
ðåàëüíûé îáúåì çàíèìàåò ìîëü ýòîãî ãàçà (ïðè í.
ó.)? Îòâåò ïîÿñíèòå.
Ðåøåíèå. Ìîëÿðíàÿ ìàññà Ì (CO2)
= 44 ã/ìîëü, òîãäà îáúåì ìîëÿ 44/1,977 = 22,12 (ë). Ýòà
âåëè÷èíà ìåíüøå ïðèíÿòîé äëÿ èäåàëüíûõ ãàçîâ
(22,4 ë). Óìåíüøåíèå îáúåìà ñâÿçàíî ñ âîçðàñòàíèåì
âçàèìî äåéñòâèÿ ìåæäó ìîëåêóëàìè ÑÎ2, ò. å.
îòêëîíåíèåì îò èäåàëüíîñòè.
Ïðèìåð 2. Ãàçîîáðàçíûé õëîð ìàññîé 0,01 ã,
íàõîäÿùèéñÿ â çàïàÿííîé àìïóëå îáúåìîì 10 ñì3,
íàãðåâàþò îò 0 äî 273oÑ. ×åìó ðàâíî íà÷àëüíîå
äàâëåíèå õëîðà ïðè 0oÑ è ïðè 273oÑ?
Ðåøåíèå. Ìr(Ñl2) =70,9; îòñþäà 0,01 ã
õëîðà ñîîòâåòñòâóåò 1,4 10-4
ìîëü. Îáúåì àìïóëû ðàâåí 0,01 ë. Èñïîëüçóÿ
óðàâíåíèå Ìåíäåëååâà-Êëàïåéðîíà pV=vRT, íàõîäèì
íà÷àëüíîå äàâëåíèå õëîðà (p1) ïðè 0oÑ:
àíàëîãè÷íî íàõîäèì äàâëåíèå õëîðà (ð2)ïðè
273oÑ: ð2 = 0,62 àòì.
Ïðèìåð 3. ×åìó ðàâåí îáúåì, êîòîðûé çàíèìàþò 10
ã îêñèäà óãëåðîäà (II) ïðè òåìïåðàòóðå 15oÑ è
äàâëåíèè 790 ìì ðò. ñò.?
Ðåøåíèå.
Çàäà÷è
1. Êàêîé îáúåì (ïðè í. ó.) çàíèìàåò 0,5
ìîëü êèñëîðîäà?
2. Êàêîé îáúåì çàíèìàåò âîäîðîä,
ñîäåðæàùèé 18-1023 ìîëåêóë (ïðè í. ó.)?
3. ×åìó ðàâíà ìîëÿðíàÿ ìàññà îêñèäà
ñåðû(IV), åñëè ïëîòíîñòü ýòîãî ãàçà ïî âîäîðîäó
ðàâíà 32?
4. Êàêîé îáúåì çàíèìàþò 68 ã àììèàêà ïðè
äàâëåíèè 2 àòì è òåìïåðàòóðå 100oÑ?
5. Â çàìêíóòîì ñîñóäå åìêîñòüþ 1,5 ë
íàõîäèòñÿ ñìåñü ñåðîâîäîðîäà ñ èçáûòêîì
êèñëîðîäà ïðè òåìïåðàòóðå 27oÑ è äàâëåíèè
623,2 ìì ðò. ñò. Íàéäèòå ñóììàðíîå êîëè÷åñòâî
âåùåñòâ â ñîñóäå.
6. Â áîëüøîì ïîìåùåíèè òåìïåðàòóðà ìîæåò
èçìåðÿòüñÿ ñ ïîìîùüþ “ãàçîâîãî” òåðìîìåòðà.
Äëÿ ýòîé öåëè ñòåêëÿííóþ òðóáêó, èìåþùóþ
âíóòðåííèé îáúåì 80 ìë, çàïîëíèëè àçîòîì ïðè
òåìïåðàòóðå 20oÑ è äàâëåíèè 101,325 êÏà. Ïîñëå
ýòîãî òðóáêó ìåäëåííî è îñòîðîæíî âûíåñëè èç
êîìíàòû â áîëåå òåïëîå ïîìåùåíèå. Áëàãîäàðÿ
òåðìè÷åñêîìó ðàñøèðåíèþ, ãàç âûøåë èç òðóáêè è
áûë ñîáðàí íàä æèäêîñòüþ, äàâëåíèå ïàðà êîòîðîé
íåçíà÷èòåëüíî. Îáùèé îáúåì ãàçà, âûøåäøåãî èç
òðóáêè (èçìåðåí ïðè 20oÑ è 101,325 êÏà), ðàâåí 3,5
ìë. Ñêîëüêî ìîëåé àçîòà ïîòðåáîâàëîñü äëÿ
çàïîëíåíèÿ ñòåêëÿííîé òðóáêè è êàêîâà
òåìïåðàòóðà áîëåå òåïëîãî ïîìåùåíèÿ?
7. Õèìèê, îïðåäåëÿâøèé àòîìíóþ ìàññó
íîâîãî ýëåìåíòà X â ñåðåäèíå XIX â., âîñïîëüçîâàëñÿ
ñëåäóþùèì ìåòîäîì: îí ïîëó÷àë ÷åòûðå ñîåäèíåíèÿ,
ñîäåðæàùèå ýëåìåíò X (À, Á, Â è Ã), è îïðåäåëÿë
ìàññîâóþ äîëþ ýëåìåíòà (%) â êàæäîì èç íèõ. Â ñîñóä,
èç êîòîðîãî ïðåäâàðèòåëüíî áûë îòêà÷àí âîçäóõ,
îí ïîìåùàë êàæäîå ñîåäèíåíèå, ïåðåâåäåííîå â
ãàçîîáðàçíîå ñîñòîÿíèå ïðè 250oÑ, è
óñòàíàâëèâàë ïðè ýòîì äàâëåíèå ïàðîâ âåùåñòâà
1,013 105 Ïà. Ïî
ðàçíîñòè ìàññ ïóñòîãî è ïîëíîãî ñîñóäîâ
îïðåäåëÿëàñü ìàññà ãàçîîáðàçíîãî âåùåñòâà.
Àíàëîãè÷íàÿ ïðîöåäóðà ïðîâîäèëàñü ñ àçîòîì. Â
ðåçóëüòàòå ìîæíî áûëî ñîñòàâèòü òàêóþ òàáëèöó:
| Ãàç | Îáùàÿ ìàññà, ã | Ìàññîâàÿ äîëÿ () ýëåìåíòà x â âåùåñòâå, % |
| N2 | 0,652 | – |
| À | 0,849 | 97,3 |
| Á | 2,398 | 68,9 |
| Â | 4,851 | 85,1 |
| Ã | 3,583 | 92,2 |
Îïðåäåëèòå âåðîÿòíóþ àòîìíóþ ìàññó ýëåìåíòà X.
8. Â 1826 ã. ôðàíöóçñêèé õèìèê Äþìà
ïðåäëîæèë ìåòîä îïðåäåëåíèÿ ïëîòíîñòè ïàðîâ,
ïðèìåíèìûé êî ìíîãèì âåùåñòâàì. Ïî ýòîìó ìåòîäó
ìîæíî áûëî íàõîäèòü ìîëåêóëÿðíûå ìàññû
ñîåäèíåíèé, èñïîëüçóÿ ãèïîòåçó Àâîãàäðî î òîì,
÷òî â ðàâíûõ îáúåìàõ ãàçîâ è ïàðîâ ïðè ðàâíîì
äàâëåíèè è òåìïåðàòóðå ñîäåðæàòñÿ îäèíàêîâûå
êîëè÷åñòâà ìîëåêóë. Îäíàêî ýêñïåðèìåíòû ñ
íåêîòîðûìè âåùåñòâàìè, ñäåëàííûå ïî ñïîñîáó
Äþìà, ïðîòèâîðå÷èëè ãèïîòåçå Àâîãàäðî è ñòàâèëè
ïîä ñîìíåíèå ñàìó âîçìîæíîñòü îïðåäåëåíèÿ
ìîëåêóëÿðíîé ìàññû äàííûì ñïîñîáîì. Âîò îïèñàíèå
îäíîãî èç òàêèõ ýêñïåðèìåíòîâ (ðèñ. 2).
à. Â ãîðëûøêå ñîñóäà à èçâåñòíîãî îáúåìà
ïîìåñòèëè íàâåñêó íàøàòûðÿ á è íàãðåëè â ïå÷è â äî
òàêîé òåìïåðàòóðû to, ïðè êîòîðîé âåñü
íàøàòûðü èñïàðèëñÿ. Ïîëó÷èâøèåñÿ ïàðû âûòåñíèëè
âîçäóõ èç ñîñóäà, ÷àñòü èõ âûäåëèëàñü íàðóæó â
âèäå òóìàíà. Íàãðåòûé äî toñîñóä,
äàâëåíèå â êîòîðîì ðàâíÿëîñü àòìîñôåðíîìó,
çàïàÿëè ïî ïåðåòÿæêå ã, çàòåì îõëàäèëè è
âçâåñèëè.
Çàòåì ñîñóä âñêðûëè, îòìûëè îò
ñêîíäåíñèðîâàííîãî íàøàòûðÿ, âûñóøèëè è ñíîâà
âçâåñèëè. Ïî ðàçíîñòè îïðåäåëèëè ìàññó m
íàøàòûðÿ.
Ýòà ìàññà ïðè íàãðåâàíèè äî toèìåëà
äàâëåíèå ð, ðàâíîå àòìîñôåðíîìó, â ñîñóäå
îáúåìîì V. Äëÿ ñîñóäà à çàðàíåå áûëè
îïðåäåëåíû äàâëåíèå è îáúåì èçâåñòíîé ìàññû
âîäîðîäà ïðè êîìíàòíîé òåìïåðàòóðå. Îòíîøåíèå
ìîëåêóëÿðíîé ìàññû íàøàòûðÿ ê ìîëåêóëÿðíîé
ìàññå âîäîðîäà îïðåäåëÿëè ïî ôîðìóëå
Ïîëó÷èëè âåëè÷èíó Ì/Ì(Í2) = 13,4.
Îòíîøåíèå, âû÷èñëåííîå ïî ôîðìóëå NH4Cl,
ñîñòàâèëî 26,8.
á. Îïûò ïîâòîðèëè, íî ãîðëûøêî ñîñóäà çàêðûëè
ïîðèñòîé àñáåñòîâîé ïðîáêîé ä, ïðîíèöàåìîé
äëÿ ãàçîâ è ïàðîâ. Ïðè ýòîì ïîëó÷èëè îòíîøåíèå Ì
/Ì(Í2) = 14,2.
â. Ïîâòîðèëè îïûò á, íî óâåëè÷èëè íà÷àëüíóþ
íàâåñêó íàøàòûðÿ â 3 ðàçà. Îòíîøåíèå ñòàëî ðàâíûì
Ì/Ì (Í2) = 16,5.
Îáúÿñíèòå ðåçóëüòàòû îïèñàííîãî ýêñïåðèìåíòà è
äîêàæèòå, ÷òî çàêîí Àâîãàäðî â äàííîì ñëó÷àå
ñîáëþäàëñÿ.
Ðåøåíèÿ
1. Ìîëü ëþáîãî ãàçà çàíèìàåò îáúåì (ïðè í. ó.) 22,4 ë;
0,5 ìîëü Î2 çàíèìàåò îáúåì 22,40,5 = 11,2 (ë).
2. ×èñëî ìîëåêóë âîäîðîäà, ðàâíîå 6,02-1023
(÷èñëî Àâîãàäðî), ïðè í. ó. çàíèìàåò îáúåì 22,4 ë (1
ìîëü); òîãäà
3. Ìîëÿðíàÿ ìàññà îêñèäà cepû(IV) : M(SO2) = 322 = 64 (ã/ìîëü).
4. Ïðè í. ó. 1 ìîëü NÍç, ðàâíûé 17 ã, çàíèìàåò îáúåì 22,4
ë, 68 ã çàíèìàåò îáúåì õ ë,
Èç óðàâíåíèÿ ãàçîâîãî ñîñòîÿíèÿ poVo/To
= p1V1/T1 íàõîäèì
5.
ñìåñè H2S
è Î2.
6. Ïðè çàïîëíåíèè òðóáêè àçîòîì
 òðóáêå îñòàëîñü (ïðè íà÷àëüíûõ óñëîâèÿõ) V1:
80-3,5 = 76,5 (ìë). Ïðè ïîâûøåíèè òåìïåðàòóðû àçîò,
çàíèìàâøèé îáúåì 76,5 ìë (V1) ïðè 20oÑ,
ñòàë çàíèìàòü îáúåì V2 = 80 ìë. Òîãäà, ñîãëàñíî
Ò1/Ò2= = V1/V2 èìååì
Ïðåäïîëîæèì, ÷òî ïðè òåìïåðàòóðå 250î
Ñ âåùåñòâà À, Á, Â, Ã ÿâëÿþòñÿ èäåàëüíûìè ãàçàìè.
Òîãäà ïî çàêîíó Àâîãàäðî
Ìàññà ýëåìåíòà X â 1 ìîëü âåùåñòâà À, Á, Â è Ã
(ã/ìîëü):
Ì(À) .0,973 = 35,45; Ì(Á) .0,689 = 70,91; Ì (Â).0,851
= 177,17; Ì(Ã).0,922= 141,78
Ïîñêîëüêó â ìîëåêóëå âåùåñòâà äîëæíî áûòü
öåëîå ÷èñëî àòîìîâ ýëåìåíòà X, íóæíî íàéòè
íàèáîëüøèé îáùèé äåëèòåëü ïîëó÷åííûõ âåëè÷èí. Îí
ñîñòàâëÿåò 35,44 ã/ìîëü, è ýòî ÷èñëî ìîæíî ñ÷èòàòü
âåðîÿòíîé àòîìíîé ìàññîé ýëåìåíòà X.
8. Îáúÿñíèòü ðåçóëüòàòû ýêñïåðèìåíòà ëåãêî
ñóìååò ëþáîé ñîâðåìåííûé õèìèê. Õîðîøî èçâåñòíî,
÷òî âîçãîíêà íàøàòûðÿ – õëîðèäà àììîíèÿ –
ïðåäñòàâëÿåò ñîáîé îáðàòèìûé ïðîöåññ
òåðìè÷åñêîãî ðàçëîæåíèÿ ýòîé ñîëè:
| NH4Cl | NH3 | + HCl. | |
| 53,5 | 17 | 36,5 |
 ãàçîâîé ôàçå íàõîäÿòñÿ àììèàê è õëîðîâîäîðîä,
èõ ñðåäíÿÿ îòíîñèòåëüíàÿ ìîëåêóëÿðíàÿ ìàññà Ìò
Ìåíåå ïîíÿòíî èçìåíåíèå ðåçóëüòàòà ïðè
íàëè÷èè àñáåñòîâîé ïðîáêè. Îäíàêî â ñåðåäèíå
ïðîøëîãî âåêà èìåííî îïûòû ñ ïîðèñòûìè
(“ñêâàæèñòûìè”) ïåðåãîðîäêàìè ïîêàçàëè, ÷òî
â ïàðàõ íàøàòûðÿ ñîäåðæàòñÿ äâà ãàçà. Áîëåå
ëåãêèé àììèàê ïðîõîäèò ñêâîçü ïîðû áûñòðåå, è åãî
ëåãêî çàìåòèòü ëèáî ïî çàïàõó, ëèáî ñ ïîìîùüþ
âëàæíîé èíäèêàòîðíîé áóìàãè.
Ñòðîãîå âûðàæåíèå äëÿ îöåíêè îòíîñèòåëüíîé
ïðîíèöàåìîñòè ãàçîâ ñêâîçü ïîðèñòûå ïåðåãîðîäêè
äàåò ìîëåêóëÿðíî-êèíåòè÷åñêàÿ òåîîèÿ ãàçîâ.
Ñðåäíÿÿ ñêîðîñòü ìîëåêóë ãàçà
, ãäå R – ãàçîâàÿ
ïîñòîÿííàÿ; Ò – àáñîëþòíàÿ òåìïåðàòóðà; Ì
– ìîëÿðíàÿ ìàññà. Ïî ýòîé ôîðìóëå àììèàê äîëæåí
äèôôóíäèðîâàòü áûñòðåå õëîðîâîäîðîäà:
Ñëåäîâàòåëüíî, ïðè ââåäåíèè â ãîðëî êîëáû
àñáåñòîâîé ïðîáêè ãàç â êîëáå óñïååò íåñêîëüêî
îáîãàòèòüñÿ òÿæåëûì ÍÑ1 çà âðåìÿ, ïîêà ïðîèñõîäèò
âûðàâíèâàíèå äàâëåíèÿ ñ àòìîñôåðíûì.
Îòíîñèòåëüíàÿ ïëîòíîñòü ãàçà ïðè ýòîì
âîçðàñòàåò. Ïðè óâåëè÷åíèè ìàññû NH4C1
äàâëåíèå, ðàâíîå àòìîñôåðíîìó, óñòàíîâèòñÿ ïîçæå
(àñáåñòîâàÿ ïðîáêà ïðåïÿòñòâóåò áûñòðîìó
âûòåêàíèþ ïàðîâ èç êîëáû), ãàç â êîëáå áóäåò
ñîäåðæàòü õëîðîâîäîðîäà áîëüøå, ÷åì â ïðåäûäóùåì
ñëó÷àå; ïëîòíîñòü ãàçà óâåëè÷èòñÿ.
Источник
Задача 28.
При 17°С некоторое количество газа занимает объем 580 мл. Какой объем займет это же количество газа при 100°С, если давление его останется неизменным?
Решение:
По закону Гей – Люссака при постоянном давлении объём газа изменяется прямо пропорционально абсолютной температуре (Т):
V2 – искомый объём газа;
T2 – соответствующая V2 температура;
V1 – начальный объём газа при соответствующей температуре Т1.
По условию задачи V1 = 580мл; Т1 = 290К (273 + 17 = 290) и Т2 = 373К (273 + 100 = 373). Подставляя эти значения в выражение закона Гей – Люссака, получим:
Ответ: V2 = 746мл.
Задача 29.
Давление газа, занимающего объем 2,5л, равно 121,6 кПа (912мм рт. ст.). Чему будет равно давление, если, не изменяя температуры, сжать газ до объема в 1л?
Решение:
Согласно закону Бойля – Мариотта, при постоянной температуре давление, производимое данной массой газа, обратно пропорционально объёму газа:
Обозначив искомое давление газа через Р2, можно записать:
Ответ: Р2 = 304кПа (2280мм.рт.ст.).
Задача 30. На сколько градусов надо нагреть газ, находящийся в закрытом сосуде при 0 °С, чтобы давление его увеличилось вдвое?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально температуре:
По условию задачи Т1 = 0 °С + 273 = 273К; давление возросло в два раза: Р2 = 2Р1.
Подставляя эти значения в уравнение, находим:
Ответ: Газ нужно нагреть на 2730С.
Задача 31.
При 27°С и давлении 720 мм.рт. ст. объем газа равен 5л. Кой объем займет это же количество газа при 39°С и давлении 104кПа?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: V = 5л; Т = 298К (273 + 25 = 298); Р = 720 мм.рт.ст. (5,99 кПа); Р0 = 104 кПа; Т = 312К (273 + 39 = 312); Т = 273К. Подставляя данные задачи в уравнение, получим:
Ответ: V0 = 4,8л
Задача 32.
При 7°С давление газа в закрытом сосуде равно 96,0 кПа. Каким станет давление, если охладить сосуд до —33 °С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:
Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 96,0 кПа; Т1 = 280К (273 + 7 = 280); Т2 = 240К (273 – 33 = 240). Подставляя эти значения в уравнение, получим:
Ответ: Р2 = 82,3кПа.
Задача 33.
При нормальных условиях 1г воздуха занимает объем 773 мл. Какой объем займет та же масса воздуха при 0 °С и )и давлении, равном 93,3 кПа (700мм. рт. ст.)?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: Р0 = 101,325кПа; V0 = 773мл; Т0 = 298К (273 + 25 = 298); Т = 273К; Р = 93,3кПа. Подставляя данные задачи и преобразуя уравнение, получим:
Ответ: V = 769, 07 мл.
Задача 34.
Давление газа в закрытом сосуде при 12°С равно 100 кПа (750мм рт. ст.). Каким станет давление газа, если нагреть сосуд до 30°С?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:
Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 100 кПа; Т1 = 285К (273 + 12 = 285); Т2 = 303К (273 + 30 = 303). Подставляя эти значения в уравнение, получим:
Ответ: Р2 = 106,3кПа.
Задача 35.
В стальном баллоне вместимостью 12л находится при 0°С кислород под давлением 15,2 МПа. Какой объем кислорода, находящегося при нормальных условиях можно получить из такого баллона?
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: V = 12л; Т = 273К (273 + 0 = 2273); Р =15,2МПа); Р0 = 101,325кПа; Т0 = 298К (273 + 25 = 298). Подставляя данные задачи в уравнение, получим:
Ответ: V0 = 1,97м3.
Задача 36.
Температура азота, находящегося в стальном баллоне под давлением 12,5 МПа, равна 17°С. Предельное давление для баллона 20,3МПа. При какой температуре давление азота достигнет предельного значения?
Решение:
При постоянном объёме давление газа изменяется прямо пропорционально абсолютной температуре:
Обозначим искомое давление через Р2, а соответствующую ему температуру через Т2. По условию задачи Р1 = 12,5МПа; Т1 = 290К (273 + 17 = 290); Р2 = 20,3МПа. Подставляя эти значения в уравнение, получим:
Ответ: Т2 = 1980С.
Задача 37.
При давлении 98,7кПа и температуре 91°С некоторое количество газа занимает объем 680 мл. Найти объем газа при нормальных условиях.
Решение:
Зависимость между объёмом газа, давлением и температурой выражается общим уравнением, объединяющим законы Гей-Люссака и Бойля-Мариотта:
где Р и V – давление и объём газа при температуре Т; Р0 и V0 – давление и объём газа при нормальных условиях. Данные задачи: Р0 = 101,325кПа; V = 680мл; Т0 = 298К (273 + 25 = 298); Т = 364К (273 + 91 = 364); Р = 98,7кПа. Подставляя данные задачи и преобразуя уравнение, получим:
<
Ответ: V0 = 542,3мл.
Задача 38.
При взаимодействии 1,28г металла с водой выделилось 380 мл водорода, измеренного при 21°С и давлении 104,5кПа (784мм рт. ст.). Найти эквивалентную массу металла.
Решение:
Находим объём выделившегося водорода при нормальных условиях, используя уравнение:
где Р и V – давление и объём газа при температуре Т = 294К (273 +21 = 294); Р0 = 101,325кПа; Т0 = 273К; Р = 104,5кПа. Подставляя данные задачи в уравнение,
получим:
Согласно закону эквивалентов, массы (объёмы) реагирующих друг с другом веществ m1 и m2 пропорциональны их эквивалентным массам (объёмам):
Мольный объём любого газа при н.у. равен 22,4л. Отсюда эквивалентный объём водорода равен 22,4 : 2 = 11,2л или 11200 мл. Тогда, используя формулу закона эквивалентов, рассчитаем эквивалентную массу металла:
Ответ: mЭ(Ме) = 39,4г/моль.
Задача 39.
Как следует изменить условия, чтобы увеличение массы данного газа не привело к возрастанию его объема: а) понизить температуру; б) увеличить давление; в) нельзя подобрать условий?
Решение:
Для характеристики газа количеством вещества (n, моль) применяется уравнение РV = nRT, или – это уравнение Клапейрона-Менделеева. Оно связывает массу (m, кг); температуру (Т, К); давление (Р, Па) и объём (V, м3) газа с молярной массой (М, кг/моль).
Тогда из уравнения Клапейрона-Менделеева объём газа можно рассчитать по выражению:
Отсюда следует, что V = const, если при увеличении массы (m) газа на некоторую величину будет соответственно уменьшена температура (T) системы на некоторое необходимое значение. Объём системы также не изменится при постоянной температуре, если при увеличении массы (m) газа на некоторую величину будет соответственно увеличено давление (P) системы на необходимую величину.
Таким образом, при увеличении массы газа объём системы не изменится, если понизить температуру системы или же увеличить давление в ней на некоторую величину.
Ответ: а); б).
Задача 40.
Какие значения температуры и давления соответствуют нормальным условиям для газов: а) t = 25 °С, Р = 760 мм. рт. ст.; б) t = 0 °С, Р = 1,013 • 105Па; в) t = 0°С, Р = 760 мм. рт. ст.?
Решение:
Состояние газа характеризуется температурой, давлением и объёмом. Если температура газа равна 0 °С (273К), а давление составляет 101325 Па (1,013 • 105) или 760 мм. рт. ст., то условия, при которых находится газ, принято считать нормальными.
Ответ: б); в).
Источник