От каких свойств маятника зависит его угловая скорость

Одним из механических объектов, демонстрирующих периодическое движение, является маятник.
Маятник-это устройство, которое движется вперед и назад, когда на него воздействует внешняя сила. Параметры маятника зависят от его длины, момента инерции и других условий. Устройства по этому принципу широко используются в часах, сейсмометрах и метрономах.
Когда на маятник воздействует внешняя сила из своего равновесного положения, он поднимается, а затем опускается под действием гравитационной силы. Угловая скорость увеличивается, когда частица находится в своей самой низкой точке, и уменьшается, когда частица достигает своей высшей точки.
История открытия
Маятники использовались в качестве сейсмометра для измерения землетрясений в первом веке династии Хань. После этого они были использованы для измерения времени египетским астрономом Ибн Юнусом в десятом веке.
Итальянский физик и астроном Галилео Галилей открыл принцип колебательного движения маятника и попытался изучить параметры и свойства этого простейшего устройства.
В 1581 году молодой Галилео Галилей, как сообщается, сделал прорывное открытие, когда он скучал во время церковной службы в Пизе. Люстра над головой мягко раскачивалась взад-вперед, но, казалось, она двигалась быстрее, когда раскачивалась широко (например, после порыва ветра), и медленнее, когда не двигалась так далеко.
Заинтригованный, Галилей решил измерить, сколько времени уходит на каждый взмах, используя единственное приблизительно периодическое событие, к которому он был готов: биение собственного пульса. Он обнаружил кое-что интересное: число ударов сердца между качаниями люстры было примерно одинаковым, независимо от того, были ли качели широкими или узкими. Величина колебаний – как далеко качался маятник взад и вперед-не влияла на частоту этих колебаний.
В своих экспериментах Галилей установил, что параметр время, необходимое для возвратно-поступательного движения маятника заданной длины, остается неизменным, даже если его дуга, или амплитуда, уменьшается. Определив параметры маятника Галилей открыл изохронизмы, наиболее важные характеристики, которые делают их полезными для измерения времени.
Галилей открыл такие свойства и параметры маятника, как: временная и периодическая независимость маятника от его амплитуды и массы.
Он сказал, что период маятника прямо пропорционален квадратному корню из длины маятника.
Кроме того в истории телескопа он также поучаствовал. Первые маятниковые часы были сконструированы сыном Галилея в 1641 году.
Маятник, происходящий от латинского слова “pendulus”, означающего “висящий”, – это тело, которое висит на неподвижной точке, которая, когда ее тянут назад и отпускают, качается взад и вперед.
Существует множество применений маятника в повседневной жизни. Некоторые примеры могут быть маятниковыми часами, которые использовались в качестве хранителя времени, метрономом, который используется для поддержания скорости музыки, акселерометрами, которые измеряют значения ускорения, и сейсмометрами, которые используются для измерения землетрясений.
Возможно, самым известным маятником является Маятник Фуко, который показал вращение Земли в середине 1800-х гг.
Почти в каждом крупном научном музее есть маятник, который можно увидеть в движении.
Система параметров устройства маятника
Инерция
Инерция маятника – сопротивление физического объекта – это то, что заставляет его качаться прямо и вверх. Нисходящая сила тяжести, которая заставляет два объекта притягиваться друг к другу, – это то, что тянет маятник прямо назад. Другая сила, сопротивление воздуха, определяющая скорость движения маятника, заставляет его раскачиваться по более коротким дугам.
Период
Период – это количество времени, которое требуется, чтобы сделать одно качание. Период маятника длиной 1 метр составляет 2 секунды.
Период связан с длиной устройства, но эта зависимость не линейна. Параметр маятника в виде периода, который в два раза длиннее другого, не просто имеет период, который также в два раза длиннее.
Амплитуда
Амплитуда-это максимальное смещение из равновесного положения. Когда маятник находится в покое, а не качается, он висит прямо вниз. Это положение называется “положением равновесия”. Это положение удобно рассматривать как исходное, упомянутое в определении как “начало координат”. При таком происхождении положение изменяется влево и вправо от начала координат. Величина наибольшего расстояния от начала координат называется амплитудой. Предмет качается на расстояние, равное амплитуде слева, а затем качается на расстояние, равное амплитуде справа.
Скорость
Скорость говорит о скорости изменения положения. Во всех случаях есть две вещи, чтобы указать скорость: скорость и направление скорости. Скорость измеряется в метрах в секунду или м/с. Направление описывается стрелкой, указывающей направление движения, или углом между этой стрелкой и исходным направлением, используемым для определения положения.
Ускорение
Ускорение – это скорость изменения скорости. Единицами измерения являются метры в секунду в квадрате или м/сек2. Указывается как величину ускорения, так и его направление. Если направление ускорения совпадает с направлением скорости, то объект ускоряется. Если направление ускорения противоположно скорости, то объект замедляется. Если направление ускорения перпендикулярно направлению скорости, то величина скорости не изменяется, но направление скорости изменяется.
Ускорение отличается от скорости удивительным образом, лучше всего описанным в трех шагах, если
- Объект оставить его в покое, он сохраняет это положение.
- Придать объекту скорость и оставить его в покое, он сохраняет эту скорость. (Этот экспериментальный факт известен как первый закон движения Ньютона.)
- Придать объекту ускорение и оставить его в покое, ускорение падает до нуля в тот момент, когда вы начинаете оставлять его в покое.
Сила
Единственный способ, которым объект ускорится (изменит скорость), – это если он вынужден это сделать. Разумно сказать, что сила имеет направление, и это направление совпадает с направлением ускорения. Большая сила вызывает большее ускорение.
Равнодействующая сила
Равнодействующая сила – это сила, возникающая в результате сочетания двух или более сил. Две силы, действующие на маятник, – это сила тяготения, тянущая прямо вниз, и сила вращения, тянущая вдоль струны к оси. Эти две силы объединяются, чтобы произвести результирующую силу. Точно так же, как стрела толкается вперед двумя половинами тетивы, объект толкается равнодействующей силой, стрела которой “расщепляет” две составляющие силы стрелы.
Гравитация
Гравитация – это название явления, которое одновременно знакомо и загадочно. Нас так уверенно тянет к Земле, что мы принимаем это как должное. Мы используем это явление, чтобы сидеть, ходить, бегать и играть в догонялки.
Экспериментально установлено, что объект, которому позволено свободно падать под действием силы тяжести, ускоряется. Поскольку объект должен быть вынужден ускоряться, должна существовать сила, связанная с гравитацией; мы называем ее силой тяготения. Направление силы тяжести – вниз. На самом деле направление силы тяжести определяет то, что мы подразумеваем под словом “вниз”.
Плоскость колебаний
Две силы: гравитация и струна определяют плоскость. Плоскость также определяется струной маятника и направлением вниз. Равнодействующая сила направлена вдоль линии, лежащей в этой плоскости. Ускорение также направлено вдоль линии, лежащей в этой плоскости.
Если объект оттянут назад и освобожден от покоя, скорость направлена вдоль той же линии, что и ускорение, и объект движется вдоль той же линии. Путь лежит вдоль плоскости, определяемой струной и гравитацией. Этот путь лежит в плоскости колебаний.
Поскольку струна и гравитация лежат в плоскости, предполагается, что плоскость колебаний никогда не изменится.
Вращение
Если положение объекта изменяется вдоль круговой траектории, говорят, что объект вращается вдоль этой окружности. Секундная стрелка аналоговых часов вращается по часовой стрелке. Особенность маятника Фуко состоит в том, что плоскость колебаний немного меняет направление по часовой стрелке в северном полушарии из-за суточного вращения Земли.
Работа
Работа – это расстояние, на которое перемещается объект, умноженное на силу, которая толкнула его на это расстояние.
Работа может быть положительной или отрицательной. Если объект движется в том же направлении, что и сила (например, когда грузовик разгоняется), то работа положительна. Если объект движется в направлении, противоположном силе (например, когда грузовик тормозит и замедляется), работа отрицательна.
Когда сила тяжести тянет вниз на предмет, который был сброшен, сила тяжести делает положительную работу на объекте.
Кинетическая энергия
Когда объект оттягивается назад и освобождается от покоя, сила тяжести положительно воздействует на него, когда он качается вниз. После того, как объект проходит через низшую точку, он качается обратно вверх, и во время этого подъема сила тяжести делает отрицательную работу, заставляя его остановиться на вершине качания.
На самом деле, объект качается назад на ту же высоту, что и высота выпуска, поэтому отрицательная работа гравитации на подъеме имеет тот же размер, что и положительная работа гравитации на спуске.
Это похоже на превращение энергии и на то, как если бы работа хранилась некоторое время, а затем возвращена обратно. При преобразовании в скорость работа, как говорят, преобразуется в кинетическую энергию. Говорят, что работа преобразуется в кинетическую энергию, когда работа делается для увеличения скорости.
Потенциальная энергия
Когда маятник оттянут назад, он готов качнуться вниз, приобретая кинетическую энергию. Количество кинетической энергии, которое он способен приобрести, определяется тем, насколько высоко был поднят объект, когда его потянули назад.
Поскольку объект обладает потенциалом для получения этой кинетической энергии, говорят, что он обладает “потенциальной энергией”. Получается, что потенциальная энергия пропорциональна высоте над самой нижней точкой качания.
Таким образом, параметры маятника – период, инерция, скорость, ускорение, гравитация, вращение, работа, потенциальная и кинетическая энергии задают свойство этого простейшего механического устройства.
Источник
Механическая система, которая состоит из материальной точки (тела), висящей на нерастяжимой невесомой нити (ее масса ничтожно мала по сравнению с весом тела) в однородном поле тяжести, называется математическим маятником (другое название – осциллятор). Бывают и другие виды этого устройства. Вместо нити может быть использован невесомый стержень. Математический маятник может наглядно раскрыть суть многих интересных явлений. При малой амплитуде колебания его движение называется гармоническим.
Общие сведения о механической системе

Формула периода колебания этого маятника была выведена голландским ученым Гюйгенсом (1629-1695 гг.). Этот современник И. Ньютона очень увлекался данной механической системой. В 1656 г. он создал первые часы с маятниковым механизмом. Они измеряли время с исключительной для тех времен точностью. Это изобретение стало важнейшим этапом в развитии физических экспериментов и практической деятельности.
Если маятник находится в положении равновесия (висит отвесно), то сила тяжести будет уравновешиваться силой натяжения нити. Плоский маятник на нерастяжимой нити является системой с двумя степенями свободы со связью. При смене всего одного компонента меняются характеристики всех ее частей. Так, если нитку заменить на стержень, то у данной механической системы будет всего 1 степень свободы. Какими же свойствами обладает математический маятник? В этой простейшей системе под воздействием периодического возмущения возникает хаос. В том случае, когда точка подвеса не двигается, а совершает колебания, у маятника появляется новое положение равновесия. При быстрых колебаниях вверх-вниз эта механическая система приобретает устойчивое положение «вверх тормашками». У нее есть и свое название. Ее называют маятником Капицы.
Свойства маятника
Математический маятник имеет очень интересные свойства. Все они подтверждаются известными физическими законами. Период колебаний любого другого маятника зависит от разных обстоятельств, таких как размер и форма тела, расстояние между точкой подвеса и центром тяжести, распределение массы относительно данной точки. Именно поэтому определение периода висящего тела является довольно сложной задачей. Намного легче вычисляется период математического маятника, формула которого будет приведена ниже. В результате наблюдений над подобными механическими системами можно установить такие закономерности:
• Если, сохраняя одинаковую длину маятника, подвешивать различные грузы, то период их колебаний получится одинаковым, хотя их массы будут сильно различаться. Следовательно, период такого маятника не зависит от массы груза.
• Если при запуске системы отклонять маятник на не слишком большие, но разные углы, то он станет колебаться с одинаковым периодом, но по разным амплитудам. Пока отклонения от центра равновесия не слишком велики, колебания по своей форме будут достаточно близки гармоническим. Период такого маятника никак не зависит от колебательной амплитуды. Это свойство данной механической системы называется изохронизмом (в переводе с греческого «хронос» – время, «изос» – равный).
Период математического маятника
Этот показатель представляет собой период собственных колебаний. Несмотря на сложную формулировку, сам процесс очень прост. Если длина нити математического маятника L, а ускорение свободного падения g, то эта величина равна:
T = 2π√L/g
Период малых собственных колебаний ни в какой мере не зависит от массы маятника и амплитуды колебаний. В этом случае маятник двигается как математический с приведенной длиной.
Колебания математического маятника
Математический маятник совершает колебания, которые можно описать простым дифференциальным уравнением:
x + ω2 sin x = 0,
где х (t) – неизвестная функция (это угол отклонения от нижнего положения равновесия в момент t, выраженный в радианах); ω – положительная константа, которая определяется из параметров маятника (ω = √g/L, где g – это ускорение свободного падения, а L – длина математического маятника (подвес).
Уравнение малых колебаний вблизи положення равновесия (гармоническое уравнение) выглядит так:
x + ω2 sin x = 0
Колебательные движения маятника
Математический маятник, который совершает малые колебания, двигается по синусоиде. Дифференциальное уравнение второго порядка отвечает всем требованиям и параметрам такого движения. Для определения траектории необходимо задать скорость и координату, из которых потом определяются независимые константы:
x = A sin (θ0 + ωt),
где θ0 – начальная фаза, A – амплитуда колебания, ω – циклическая частота, определяемая из уравнения движения.
Математический маятник (формулы для больших амплитуд)
Данная механическая система, совершающая свои колебания со значительной амплитудой, подчиняется более сложным законам движения. Для такого маятника они рассчитываются по формуле:
sin x/2 = u * sn(ωt/u),
где sn – синус Якоби, который для u < 1 является периодической функцией, а при малых u он совпадает с простым тригонометрическим синусом. Значение u определяют следующим выражением:
u = (ε + ω2)/2ω2,
где ε = E/mL2 (mL2 – энергия маятника).
Определение периода колебания нелинейного маятника осуществляется по формуле:
T = 2π/Ω,
где Ω = π/2 * ω/2K(u), K – эллиптический интеграл, π – 3,14.
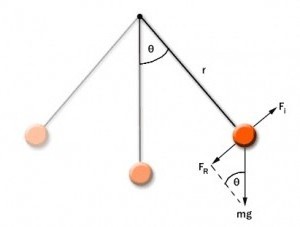
Движение маятника по сепаратрисе
Сепаратрисой называют траекторию динамической системы, у которой двумерное фазовое пространство. Математический маятник движется по ней непериодически. В бесконечно дальнем моменте времени он падает из крайнего верхнего положения в сторону с нулевой скоростью, затем постепенно набирает ее. В конечном итоге он останавливается, вернувшись в исходное положение.
Если амплитуда колебаний маятника приближается к числу π, это говорит о том, что движение на фазовой плоскости приближается к сепаратрисе. В этом случае под действием малой вынуждающей периодической силы механическая система проявляет хаотическое поведение.
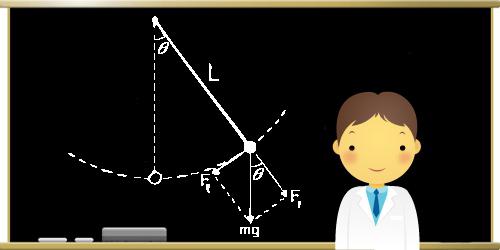
При отклонении математического маятника от положения равновесия с некоторым углом φ возникает касательная силы тяжести Fτ = –mg sin φ. Знак «минус» означает, что эта касательная составляющая направляется в противоположную от отклонения маятника сторону. При обозначении через x смещения маятника по дуге окружности с радиусом L его угловое смещение равняется φ = x/L. Второй закон Исаака Ньютона, предназначенный для проекций вектора ускорения и силы, даст искомое значение:
mg τ = Fτ = –mg sin x/L
Исходя из этого соотношения, видно, что этот маятник представляет собой нелинейную систему, поскольку сила, которая стремится вернуть его в положение равновесия, всегда пропорциональна не смещению x, а sin x/L.
Только тогда, когда математический маятник осуществляет малые колебания, он является гармоническим осциллятором. Иными словами, он становится механической системой, способной выполнять гармонические колебания. Такое приближение практически справедливо для углов в 15–20°. Колебания маятника с большими амплитудами не является гармоническим.
Закон Ньютона для малых колебаний маятника

Если данная механическая система выполняет малые колебания, 2-й закон Ньютона будет выглядеть таким образом:
mg τ = Fτ = –m* g/L* x.
Исходя из этого, можно заключить, что тангенциальное ускорение математического маятника пропорционально его смещению со знаком «минус». Это и является условием, благодаря которому система становится гармоническим осциллятором. Модуль коэффициента пропорциональности между смещением и ускорением равняется квадрату круговой частоты:
ω02 = g/L; ω0 = √ g/L.
Эта формула отражает собственную частоту малых колебаний этого вида маятника. Исходя из этого,
T = 2π/ ω0 = 2π√ g/L.
Вычисления на основе закона сохранения энергии
Свойства колебательных движений маятника можно описать и при помощи закона сохранения энергии. При этом следует учитывать, что потенциальная энергия маятника в поле тяжести равняется:
E = mg∆h = mgL(1 – cos α) = mgL2sin2 α/2
Полная механическая энергия равняется кинетической или максимальной потенциальной: Epmax = Ekmsx = E
После того как будет записан закон сохранения энергии, берут производную от правой и левой частей уравнения:
Ep + Ek = const
Поскольку производная от постоянных величин равняется 0, то (Ep + Ek)’ = 0. Производная суммы равняется сумме производных:
Ep’ = (mg/L*x2/2)’ = mg/2L*2x*x’ = mg/L*v + Ek’ = (mv2/2) = m/2(v2)’ = m/2*2v*v’ = mv* α,
следовательно:
Mg/L*xv + mva = v (mg/L*x + m α) = 0.
Исходя из последней формулы находим: α = – g/L*x.
Практическое применение математического маятника
Ускорение свободного падения изменяется с географической широтой, поскольку плотность земной коры по всей планете не одинакова. Там, где залегают породы с большей плотностью, оно будет несколько выше. Ускорение математического маятника нередко применяют для геологоразведки. В его помощью ищут различные полезные ископаемые. Просто подсчитав количество колебаний маятника, можно обнаружить в недрах Земли каменный уголь или руду. Это связано с тем, что такие ископаемые имеют плотность и массу больше, чем лежащие под ними рыхлые горные породы.
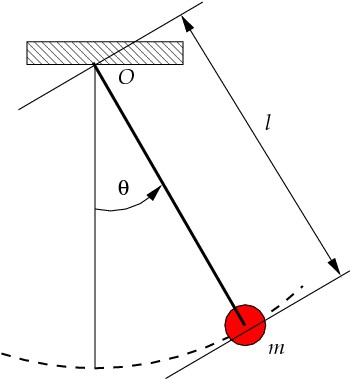
Математическим маятником пользовались такие выдающиеся ученые, как Сократ, Аристотель, Платон, Плутарх, Архимед. Многие из них верили в то, что эта механическая система может влиять на судьбу и жизнь человека. Архимед использовал математический маятник при своих вычислениях. В наше время многие оккультисты и экстрасенсы пользуются этой механической системой для осуществления своих пророчеств или поиска пропавших людей.
Известный французский астроном и естествоиспытатель К. Фламмарион для своих исследований также использовал математический маятник. Он утверждал, что с его помощью ему удалось предсказать открытие новой планеты, появление Тунгусского метеорита и другие важные события. Во время Второй мировой войны в Германии (г. Берлин) работал специализированный Институт маятника. В наши дни подобными исследованиями занят Мюнхенский институт парапсихологии. Свою работу с маятником сотрудники этого заведения называют «радиэстезией».
Источник
