Определи по рисункам каким свойством обладают элементы пересечения множеств
Математика часто оперирует абстрактными объектами, для задания связи между которыми существуют различные операции, такие как пересечение и объединение множеств.
Понятие множества является интуитивным, не определяемым. Оно обычно ассоциируется с набором чего-либо, группой каких-то предметов или живых объектов, совокупностью некоторых условий, рассматривается как класс, семейство в некоторой классификации, промежуток числовой прямой. Например, в геометрии рассматриваются линии как множества точек.
То, из чего состоит множество, называется его элементами.
Графическим изображением, служащим для наглядности рассматриваемых объектов, является круг Эйлера.
Что такое пересечение множеств
Для любого набора множеств их пересечением называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из заданных. Другими словами, это совокупность всех общих элементов.
С помощью кругов Эйлера-Венна пересечение можно изобразить так:
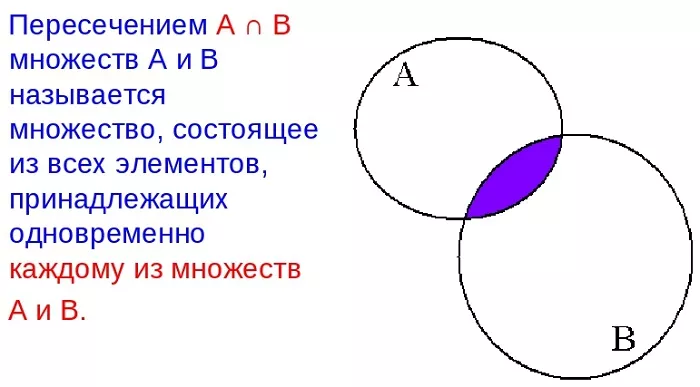
Знак пересечения: ∩.
Часто применяется для определения решений систем уравнений и неравенств.
Ассоциируется с обычным умножением двух числовых объектов.
Что такое объединение множеств
Для любого набора множеств, их объединением называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из заданных.
Изображение кругами Эйлера выглядит следующим образом:
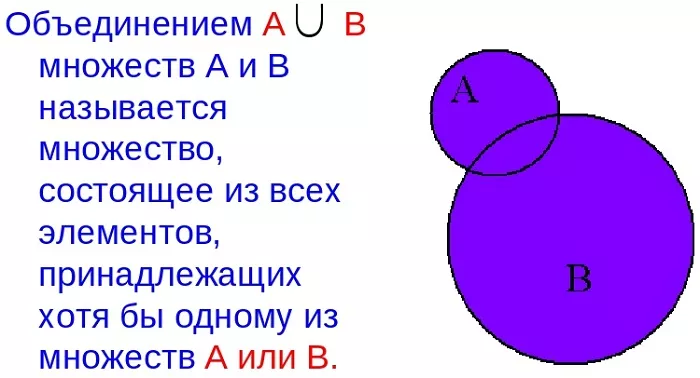
Знак объединения: ∪.
Часто используется при решении уравнений и неравенств, подчёркивая наличие серий корней и решений, нескольких используемых промежутков числовой прямой.
В обычной математике близко по смыслу с операцией, называемой «сложение».
Для решения задач нужно знать о следующих свойствах:
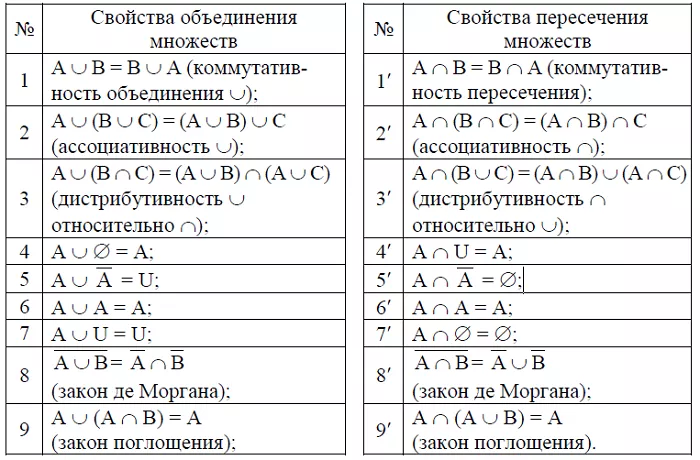
1. Коммутативность (перестановочность):
A ∩ B = B ∩ A;
A ∪ B = B ∪ A.
Эти свойства распространяются на любое количество компонентов. Следуют из определения операций.
2. Ассоциативность (расстановка скобок):
(A ∩ B) ∩ C = A ∩ (B ∩ C);
(A ∪ B) ∪ C = A ∪ (B ∪ C).
Данные свойства также применимы к большому количеству компонентов. Позволяют опускать скобки и упрощать запись.
3. Дистрибутивность (раскрытие скобок):
(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C);
(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C).
4. Закон идемпотентности (идентичности):
A ∩ A = A;
A ∪ A = A.
Множество, не содержащее ни одного элемента, называется пустым. Обозначается перечёркнутым нулём: Ø
Выполнение операций с Ø:
A ∩ Ø = Ø;
A ∪ Ø = Ø.
Прослеживается аналог со сложением и умножением на ноль.
Операции над множествами
Помимо объединения и пересечения существуют другие операции:
Для двух множеств A и B можно определить их разность как набор элементов, входящих в A и не содержащихся в B:
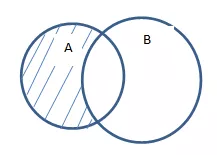
(AB)
Рассматривая некоторое множество в качестве содержащего все остальные, можно прийти к понятию «дополнение», как к совокупности всех элементов, не входящих в A:
Благодаря этой операции свойства объединения и пересечения можно расширить/
Закон де Моргана:
![]()
![]()
Примеры решения задач
Задача №1
B A, B ∪ A.
Пусть
![]()
Выписать все элементы множества
![]()
где
![]()
Решение.
При поиске M операции выполняются последовательно.
B A состоит из всех элементов B, которые не принадлежат A, поэтому:
![]()
B ∪ A включает в себя все элементы, принадлежащие хотя бы одному из множеств A или B. Таким образом:
![]()
M = (B A) (B ∪ A) состоит из всех элементов B A, которые не принадлежат B ∪ A, следовательно, M = Ø.
Задача №2
Доказать методом включений тождество:
![]()
Решение.
Необходимо доказать выполнение включений:
![]()
и
![]()
Шаг 1.
Выбирается произвольный x из (A ∩ B) ∪ C. По определению операции объединения x ∈ B ∩ A или x ∈ C.
Если x ∈ B ∩ A, то по определению пересечения x ∈ B и x ∈ A.
Так как x ∈ A, то x ∈ C ∪ A; так как x ∈ B, то x ∈ C ∪ B, следовательно, x ∈ (A ∪ C) ∩ (B ∪ C).
Если x ∈ C, то x ∈ C ∪ A и x ∈ C ∪ B, а значит: x ∈ (A ∪ C) ∩ (B ∪ C).
Поскольку x ∈ (A ∩ B) ∪ C был выбран произвольно, утверждается, что любой элемент этого множества содержится в (A ∪ C) ∩ (B ∪ C), то есть:
![]()
Шаг 2.
Выбирается произвольный y из (A ∪ C) ∩ (B ∪ C).
По определению операции пересечения y ∈ C ∪ A и y ∈ C ∪ B.
Так как y ∈ C ∪ A, то y ∈ A или y ∈ C; так как y ∈ C ∪ B, то y ∈ C или y ∈ B. Таким образом, y ∈ C или y ∈ A и y ∈ B.
Если y ∈ A и y ∈ B, то y ∈ B ∩ A, а, следовательно, y ∈ (A ∩ B) ∪ C; если y ∈ C, то также y ∈ (A ∩ B) ∪ C.
Поскольку y из (A ∪ C) ∩ (B ∪ C) выбирался произвольно, утверждается, что любой элемент этого множества содержится в (A ∩ B) ∪ C, то есть
![]()
Шаг 3.
Из пунктов 1 и 2 вытекает, что
![]()
Доказано.
Источник
Урок по математике
в 6 классе
Тема: «Пересечение и объединение множеств»
Учитель математики
МБОУ «Кабановская СОШ»
Жукова В.В.
ПЛАН-КОНСПЕКТ УРОКА
Тема урока: «Пересечение и объединение множеств».
Тип урока: изучение нового материала.
Цели:
формирование знаний о пересечении и объединении множеств;
развитие умений и нахождение числа элементов пересечения и объединения множеств, выявлять закономерность, обобщать и делать выводы, воспитание ответственного отношения к учебе.
Ход урока.
1. Организационный момент.
2. Повторение изученного по теме «Множества».
Вопросы для учащихся:
Что такое множество?
Что такое элементы множества?
Какое множество конечно и бесконечно?
Какое множество называется пустым?
3. Изучение нового материала «Пересечение множеств».
Учитель. Рассмотрим следующие два множества: М – множество всех точек круга, N – множество точек прямой, пересекающей круг. Каждый видит, что пересечение круга с прямой – это отрезок; обозначим его концы буквами А и В. Задумаемся: каким свойством обладают точки этого отрезка по отношению к множествам М и N? Ответ ясен: точки отрезка АВ – это в точности те точки, которые принадлежат и множеству М, и множеству N. Так что множество всех точек отрезка АВ естественно назвать пересечением множеств М и N.

Точно так же можно определить пересечение любых двух множеств М и N. Пересечением множеств М и N называется множество, состоящее из всех элементов, принадлежащих каждому из множеств М и N. Пересечение множеств М и N обозначают МN. Читают: «пересечение М и N» или «М пересечение N». Знак называется знаком пересечения.
Обсудим несколько примеров.
Пример 1. М – множество всех учениц какой-то школы, N – множество всех учащихся данного класса этой школы. Тогда МN – это множество всех девочек из данного класса.
Пример 2. М – множество всех квартир на 1-м этаже в каком-то доме, N – множество всех квартир в данном подъезде этого дома. Тогда МN – это множество всех квартир на 1-м этаже в данном подъезде.
Пересечение множеств точек двух фигур на плоскости легче представить, если нарисовать эти фигуры. Сделаем это, например, для двух кругов. Множество всех точек первого круга обозначим М, второго – N. Для пересечения МN могут быть три варианта; они изображены на рисунке.
Ø
Если конечные множества записаны при помощи фигурных скобок списками своих элементов, то легко записать их пересечение. Примеры:
=;= ;
=; .
Пересечение можно образовывать не только для двух множеств, но и для любого их числа. Определяется это точно так же, как и для двух множеств: пересечением данных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из этих множеств. Пересечение множеств М, N и Р обозначается МNР.
Вопрос для учащихся:
Что обозначает запись РQRS? Какому множеству равно это пересечение, если Р=; Q=; R=; S=?
4. Первичное закрепление понятия пересечения множеств.
Вопросы:
Что такое пересечение двух множеств; нескольких множеств?
Что значит, что два множества не пересекаются? Приведите 2-3 примера непересекающихся множеств.
Какое множество обозначается знаком ?
Практические задания:
1. Для каждой пары множеств М и Nзапишите их пересечение:
М=, N=;
М=, N=;
М=, N=;
,N – множество всех неправильных дробей.
2. Для каждой пары множеств М и N укажите их пересечение:
М – множество всех нечетных чисел, N – множество всех натуральных чисел, делящихся на 4;
М – множество всех правильных дробей, N – множество всех десятичных дробей;
М – множество всех натуральных чисел, делящихся на 3, N – множество всех натуральных чисел, делящихся на 5.
3. Дан многоугольник. Каждую его сторону будем рассматривать как множество всех точек, принадлежащих этой стороне. Для каждой пары сторон многоугольника укажите множество, равное пересечению этих двух сторон, если многоугольник – это: а) треугольник АВС; б) прямоугольник KLMN.
4. Рассмотрите три множества , и . Убедитесь, что их пересечение пусто, а пересечение любых двух из этих множеств не пусто.
5. Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.
Запишите всевозможные попарные пересечения этих множеств. Имеются ли среди них равные?
Запишите всевозможные пересечения троек этих множеств. Имеются ли среди них равные?
Запишите пересечение всех этих множеств. Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?
5. Изучение нового материала «Объединение множеств».
Учитель. Объединением множеств М и N называется множество всех элементов, принадлежащих хотя бы одному из множеств М и N. Объединение множеств М и N обозначают МN. Читают: «объединение М и N» или «М объединение N». Знак называется знаком объединения.
Разберем несколько примеров. Обдумайте каждый из них.
Пример 1. М – множество всех учеников данного класса, получивших на сегодняшний день пятерку по какому-нибудь предмету, N – множество всех учеников того же класса, получивших в этот день четверку по какому-нибудь предмету. Тогда МN – это множество всех учеников данного класса, получивших за сегодняшний день повышенные отметки.
Пример 2. М – множество всех правильных дробей, N – множество всех неправильных дробей. Тогда МN – это множество всех обыкновенных дробей.
Пример 3. М – множество всех букв слова КОШКА, N – множество всех букв слова МЫШКА. Тогда МN =.
Задание для учащихся:
Приведите сами какой-нибудь пример объединения двух множеств.
Учитель. Как и пересечение, объединение можно образовать не только для двух множеств, но и для любого их числа: объединением данных множеств называется множество, состоящее…
Закончите определение. Догадайтесь, как записать объединение трех множеств М, N и Р.
Если конечные множества записаны при помощи фигурных скобок списками своих элементов, то, как и для пересечения, легко записать их объединения.
=;
=;
=;
=.
Для любых множеств М и N можно образовать их пересечение МN и объединение МN. Это похоже на то, что происходит при действиях над числами: для любых двух чисел m и n можно образовать их произведение m n и сумму m+n. Так получаются действия, которые назвали умножением и сложением. Поэтому образование пересечения и образование объединения можно назвать действиями над множествами.
Выполняются ли те же законы для пересечения и объединения множеств? Давайте рассуждать. Начнем с переместительного закона. Повторим, что такое пересечение двух множеств: множество МN состоит из всех элементов, принадлежащих каждому из множеств М и N, а множество NМ состоит из всех элементов, принадлежащих каждому из множеств Nи М. Но сказать «каждому из множеств М и N» или «каждому из множеств Nи М» – значит сказать одно и то же: ведь ясно, что неважно, в каком порядке перечислять здесь множества. Значит, множества МN и NМ состоят из одних и тех же элементов, т.е.
МN=NМ
Данное равенство и означает, что переместительный закон для пересечения верен.
Чтобы проверить сочетательный закон, надо убедиться, что для любых трех множеств М, N и Р выполняется равенство
М(NР)= (МN)Р
Легко понять, что в левой и правой частях этого равенства записаны множества, состоящие из всех элементов, принадлежащих каждому из множеств М, N и Р, т.е. состоящие из одних и тех же элементов. Это и означает, что требуемое равенство выполняется.
6. Первичное закрепление изученного понятия объединения множеств.
Вопросы:
Что такое объединение двух множеств; нескольких множеств?
О выполнении каких законов для действий пересечения и объединения множеств идет речь в объяснительном тексте этого параграфа?
Каким множеством – конечным или бесконечным – будет объединение: а) двух конечных множеств; б) двух бесконечных множеств; в) конечного и бесконечного множеств?
Практические задания:
1. Для каждой пары множеств М и N запишите их объединение:
М=, N=;
М=, N=;
М=, N=.
2. Для каждой пары множеств М и N укажите их объединение:
М – множество всех нечетных чисел, N – множество всех четных чисел;
М – множество всех квадратов на плоскости, N – множество всех прямоугольников на той же плоскости, четырехугольников;
М – множество всех натуральных чисел, делящихся на 3, N – множество всех натуральных чисел, делящихся на 15.
3. Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.
Запишите всевозможные попарные объединения этих множеств. Имеются ли среди них равные?
Запишите всевозможные объединения троек этих множеств. Имеются ли среди них равные?
Запишите объединение всех этих множеств. Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?
7. Изучение нового – вывод правила подсчета числа элементов объединения и пересечения множеств.
Учитель. Чтобы вывести правило давайте разберем конкретный пример. Пусть М=, т.е. m=4;
N=, т.е. n=3.
Запишем объединение этих множеств:
МN=.
В множестве МN пять элементов, а m+n=4+3=7. Вот мы и видим, что в МN элементов меньше чем 7.
Почему так получилось? Да потому, что в данном примере можно указать учеников, которые в этот день получили и пятерку, и четверку. Другими словами здесь пересечение МN не пусто: МN=. Но в объединении-то МN каждый элемент пересечения МN присутствует (и подсчитывается) только один раз, а не два раза.
Давайте-ка изобразим ситуацию нашего примера на рисунке.
Если бы подсчитали здесь сумму m+n (т.е. 4+3), то каждый элемент пересечения (в данном примере Валя и Игорь, т.е. 2 элемента) оказался бы подсчитанным дважды. Значит, чтобы узнать число элементов объединения, надо из суммы m+n вычесть число лишний раз сосчитанных элементов пересечения. В данном примере получаем 4+3-2=5.
Данная задача была решена с помощью рисунка, этот способ называется «Круги Эйлера». Леонард Эйлер – швейцарский математик, который в 18 веке работал в Российской академии наук и сделал много открытий для нашей науки.
Итак, если мы возьмем сумму m+n, то в ней элементы пересечения МN будут сосчитаны дважды. Значит, чтобы определить число элементов объединения, надо из суммы m+n вычесть число лишний раз сосчитанных элементов из МN, т.е. число р. Получим такую формулу:
q=m+n-p.
Сформулируем правило для нахождения числа элементов объединения множеств:
Чтобы найти число элементов объединения двух множеств, надо сложить числа элементов этих множеств и вычесть из полученной суммы число элементов их пересечения.
Сформулируем правило для нахождения числа элементов пересечения множеств:
Чтобы найти число элементов пересечения двух множеств, надо сложить числа элементов этих множеств и вычесть из полученной суммы число элементов их объединения.
8. Первичное закрепление изученного.
Практические задания (устно):
1. Вычислите число элементов в объединении множеств М и N, если:
М содержит 10 элементов, N – 15 элементов, а МN – 7 элементов;
М содержит 27 элементов, N – 18 элементов, а МN – 13 элементов;
М содержит 45 элементов, N – 57 элементов, а МN – 1 элемент.
2. Вычислите число элементов в пересечении множеств М и N, если:
М содержит 10 элементов, N – 15 элементов, а МN – 17 элементов;
М содержит 27 элементов, N – 18 элементов, а МN – 45 элементов;
М содержит 45 элементов, N – 57 элементов, а МN – 100 элементов.
Решение задач с помощью кругов Эйлера:
№1. В классе 28 учеников. Каждый из них начертил у себя в тетради один из двух четырехугольников – прямоугольник или ромб. При проверке прямоугольников оказалось 17, а ромбов – 15. Как такое могло случиться?
№2. В осенние каникулы 12 учеников класса участвовали в междугородных экскурсиях в Москву и Санкт-Петербург, при этом 8 из них посетили Санкт-Петербург, а 6 – Москву. Сколько из этих учеников побывало и в Москве, и в Санкт-Петербурге?
Задание на дом:
№1. Найдите пересечение множеств учителей, которые вели уроки в вашем классе: а) вчера и сегодня; б) вчера и позавчера. Оказалось ли какое-то из этих двух пересечений пустым?
№2. Вася, рассматривая свой дневник погоды, обнаружил, что в сентябре 17 раз отмечен дождь и 19 раз – сильный ветер. При этом дней, когда одновременно шел дождь и дул сильный ветер, оказалось 7. Был ли хоть один день, когда не было ни дождя, ни сильного ветра?
Источник
Основные цели:
1) формировать представление о переместительном и сочетательном свойствах операции пересечения множеств;
2) повторить переместительное и сочетательное свойства сложения и умножения, закрепить понятие пресечения множеств;
3) тренировать навыки решения уравнений и задач на приведение к единице.
Познавательные УУД:
использование имеющихся знаний;
исследование учебной задачи;
установление логических, причинно-следственных связей, построение логической цепи рассуждений,
применение знаково-символической схемы.
Регулятивные УУД:
оценивать уровень успешности;
производить контроль своих действий;
определять цель учебной задачи;
планировать свою деятельность, определяемую результатом,
контроль в форме сличения способа действия и его результата с заданным эталоном.
Коммуникативные УУД:
умение слушать и вступать в диалог;
умение правильно выражать свои мысли;
умение контролировать и корректировать действия других;
оформление своей мысли в устной речи;
обоснование своего ответа;
умение ориентироваться в своей системе знаний;
Личностные УУД:
самооценка своих возможностей;
формирование положительного отношения к учению.
Мыслительные операции, необходимые на этапе проектирования: сравнение, обобщение, аналогия.
Демонстрационный материал:
1) карточки с высказываниями:
«Новое умение — везде найдёт применение».
«Торопись — да не ошибись».
«Повторение — мать учения».
2) карточки с записями:
3) карточки с записью свойств чисел:
а + b = b + а (а + b) + с = а + (b + с)
а · b = b · а (а · b) · с = а · (b · с)
4) карточки для составления эталона:
А ∩ В = В ∩ А
(А ∩ В) ∩ С = А ∩ (В ∩ С)
(А ∩ В) ∩ С = А ∩ (В ∩ С)
Пересечение множеств не зависит
от порядка множеств …
…и от изменения порядка действий.
5) алгоритм рассуждений для вычислений:
Читаю выражение
Определяю свойство, которое можно использовать для упрощения вычислений
Вычисляю
6) эталон для самопроверки к этапу 7:
М ∩ К = К ∩ М Пересечение множеств не зависит
от порядка множеств и порядка
(М ∩ К) ∩ Т = М ∩ (К ∩ Т) действий.
7) «лесенка успеха» Я УЗНАЛ НАУЧИЛСЯ ЗАПОМНИЛ УДИВИЛСЯ
Раздаточный материал:
Листы для выполнения заданий для пробного действия.
Самопроверка к заданиям по выбору (задача)
4 под. – n кв.
6 под. — ? кв.
1 под. — ? кв.
Ответ: 96 квартир в 6 подъездах.
Самопроверка к заданиям по выбору (уравнения)
а
б) 604 – х = 286; 604
х = 604 – 286; 286
х = 318. 318
604 – 286 = 318
318 =318
) х – 394 = 286; 286
х = 286 + 394; 394
х = 670 670
286 + 394 = 670
670 = 670
Самопроверка к заданиям по выбору (примеры)
а) (13 + 8 · 4 ) : 5 – (27 : 3 – 0 · 6) = 9 – 9 = 0
9
32
45 9
б) 40 : (24 : 6) + 7 · (12 – 2 · 2) – 5 · 5 = 10+ 56 – 25 = 10 + 56 – 25 = 41
4 4 25
10 56 8
Ход урока:
1. Мотивация к учебной деятельности.
Цель:
1) создать условия для возникновения у учащихся внутренней потребности включения в учебную деятельность («хочу») через создание ситуации, вызывающей интерес;
2) организовать деятельность учащихся по установке тематических рамок урока («могу»): пересечение множеств.
3) организовать актуализацию требований к ученику со стороны учебной деятельности («надо»).
Организация учебного процесса на этапе 1:
1)- Ребята к нам сегодня пришли гости. Давайте поздороваемся.
– Вы любите тайны? (Да)
Сегодня на уроке мы с вами будем раскрывать математические тайны.
Давайте подумаем каким образом вы будите это делать? (С повторения того, что нам пригодится для открытия нового.)
– Пожелайте друг другу удачи и поднимаясь по нашей математической лестнице вы сможете узнать новую тайну.
Организация учебного процесса на этапе 2:
К нам в гости на урок пришла буква Я, которая вместе с нами будет раскрывать математические тайны.(На доску вывешивается буква Я).
Предлагаю вам до повторения необходимого потренироваться в устном счёте. (Под первой ступенькой появляется слово повторение).
Кто сегодня подготовил математический диктант? Кто? (Сафронова А.)
33 больше задуманного числа на 8. Какое число задумано?
Задуманное число меньше 42 на 10. Какое число задумано?
Какое число надо прибавить к 17, чтобы получить 56?
Какое число надо вычесть из 61, чтобы получить 15?
70 больше неизвестного числа на 17. Чему равно неизвестное число?
44 меньше неизвестного числа на 16. Чему равно неизвестное число?
– Проверим. (25; 32; 39; 46; 53, 60; ).
– Посмотрите закономерность и скажите следующие три числа в данном ряду чисел. (Числа увеличиваются на 7. Следующее число 67;74; 81.)
Соотнесите числа с буквами в порядке убывания и вы узнаете какому разделу математики будет посвящён урок.
25 32 39 46 53 60 67 74 81(СЛАЙД)
О В Т С Е Ж О Н М
– Какое слово получилось?
– Раскрываем следующую тайну.
Посмотрите на множества.(На проекторе диаграмма пересекающихся множеств А и В.)(СЛАЙД)
В
Перечислите элементы множества А и множества В.
Что значит «общие элементы» множеств? (В множестве А есть такие же элементы, как и в множестве В.)
Где находится точка 2? (На пересечении этих двух множеств.)
Что называют «пересечением» множеств? (Правило). На доске появляется стебель (цветка) со словом ПЕРЕСЕЧЕНИЕ).
На слайде — математические выражения:
(5 48) 2
2) Актуализация представлений о переместительном и сочетательном свойствах сложения и умножения.
Назовите эту запись математическим термином. (Выражение.)
Какие свойства операций умножения вы знаете? (Переместительное, сочетательное и распределительное.)
Для чего используют эти свойства? (Для удобства вычислений.)
Найдите значение этого выражения, пользуясь свойствами. Каким свойством вы воспользуетесь? (Сочетательным. От изменения порядка действий произведение не изменяется.) Назовите сочетательное свойство.
Учитель вывешивает эталон с лепестком:
(a · b) · c = a · (b · c)
-Примените сочетательное свойство умножения при решении этого выражения.
(Дети делают самостоятельно)
– Скажите, какие множители вы сгруппировали.(5и2)
– Проверьте свою запись.(Слайд)
(5 · 48) · 2 = (5 · 2) · 48 = 10 · 48 = 480.
– Каким свойством мы сейчас пользовались?(Сочетательным)
– А если знак умножения заменить на знак плюс, что мы получим?
(Сочетательное свойство сложения)
– Давайте хором его назовём.((a + b) + c = a + (b + c)
(Вывешиваю лепесток на доску)
– Какие свойства мы повторили?(сочетательное свойство умножения и сочетательное свойство сложения)(Слайд)
– На проекторе новое выражение(СЛАЙД)
259 + 648…648 + 259
Посмотрите на следующее выражение. Какой знак надо поставить между выражениями?(=)
– Почему?(Они равны)
Каким свойством вы воспользуетесь? (Переместительным. От перестановки слагаемых сумма не изменяется.)
a + b = b + a (вывешиваю свойство)
Какое ещё переместительное свойство вы знаете?(Переместительное свойство умножения)
– Назовите его.( a · b = b · a )
(Вывешиваю на доску лепесток)
Давайте назовём, что мы с вами сейчас повторили? ( Показываю на цветке и повторяю с детьми (Множество, пересечение, переместительное и сочетательные свойства умножения и сложения, сравнивали выражения).
Давайте произнесём какие главные слова были у нас на этом этапе повторения? (Множество, пересечение, свойство)
Кто может используя эти слова сформулировать тему нашего урока? («Свойства пересечения множеств».)
(Учитель вывешивает кружок в середину цветка с названием темы на доску и буква Я переходит на лестницу НОВОЕ).
Значит, какую цель поставим перед собой? (Выяснить, обладает ли пересечение множеств переместительным и сочетательным свойствами, записать и сформулировать его.)
3. Выявление места и причины затруднения.
Цель:
1) организовать восстановление выполненных операций и фиксацию (вербальную и знаковую) места – шага, операции, где возникло затруднение;
2) организовать соотнесение действий учащихся с используемым способом (алгоритмом, понятием и т.д.) и на этой основе организовать выявление и фиксирование во внешней речи причины затруднения – тех конкретных знаний, умений или способностей, которых недостаёт для решения исходной задачи такого класса или типа.
На проекторе появляется.(CЛАЙД)
А ∩ В … В ∩ А
(А ∩ В) ∩ С …..А ∩ (В ∩С)
– Что нового в этом задании? (Надо определить, верны равенства с пересечениями или нет, а мы такого никогда не делали).
– Попробуйте выполнить задание на маркерных досках.
– Проверим выполнение. Кто не справился с заданием? Почему возникла у вас проблема? (Мы не можем определить, равны эти пересечения или нет.)
– Кто определил, верны или нет эти равенства?
Какое задание вы выполняли? (Мы должны были определить, верно ли то, что пересечения множеств равны.)
Как вы выполняли задания? (…)
Где у вас возникло проблема?
Почему она возникло? (У нас нет правила, эталона, чтобы определить, верны ли эти равенства.)
– Давайте вернёмся к числовым выражениям.
Что помогло нам сравнить числовые выражения? (Свойства сложения и умножения.)
Посмотрите на эталоны, которые висят на доске. На какие из них похожи данные равенства? (Первая – на переместительное свойство умножения и сложения, вторая – на сочетательное…)
А, может быть, данными свойствами обладают и пересечения множеств? И именно эти знания помогут нам.
– Вспомните ещё раз, что мы повторяли. Подумайте, что поможет вам доказать, что пересечения множеств обладают свойствами сочетательным и переместительным.
Проверим, обладает операция пересечения множеств переместительным и сочетательным свойствами или нет.Сейчас мы будем работать в группе. Не забывайте как надо работать в группе.
– Умеем мы задавать множества? Умеем обозначать их на диаграммах?
Проверим, обладает операция пересечения множеств переместительным и сочетательным свойствами или нет.
Форма работы: групповая на планшетах.
– Перед вами задание №1. Прочитайте внимательно задание и выполните его на маркерных досках.
1. Задайте множества А и В пересечением.
– Изобразите с помощью диаграммы Венна множество А, множество В. Что заметили? Сделайте вывод. (Они имеют общие элементы, их пересечение равно…)
Изобразим множество В, множество А. Что заметили?
Сделайте вывод. (Получился такой же результат.)
Какой вывод вы можете сделать? (Пересечение множеств обладает переместительным свойством.)
– 2. Задайте множества А , В и С пересечением.
– Изобразите с помощью диаграммы Венна множество А, множество В и множество С. Что заметили? (Они имеют общие элементы, их пересечение равно…)
– Какой вывод можете сделать? (Пересечение множеств обладает сочетательным свойством).
– Где можем проверить наш вывод? (В учебнике.)
Обращаются к учебнику стр. 27, проверяют себя.
– Что мы доказали? (Что пересечение множеств обладает переместительным и сочетательным свойствами, а стало быть, предложенные нам равенства верны.)
Справились с проблемой? (Да.)
Молодцы! Вы открыли ещё одну математическую тайну. Учитель вывешивает на доску два лепестка со свойствами пересечения множеств.
4.ФИЗКУЛЬТМИНУТКА
5. Первичное закрепление.
Цель:
зафиксировать изученные свойства множеств в записи.
1) На проекторе появилось выражение: (СЛАЙД)
«НОВОЕ УМЕНИЕ ВЕЗДЕ НАЙДЁТ ПРИМЕНЕНИЕ».
Как вы думаете, чем займёмся? (Будем применять новое умение в заданиях.)
Н
Задание:
А = {1; 2; 3; 4}, В = {3; 4; 5}. Запиши с помощью фигурных скобок множества
А ∩ В и В ∩ А. Отметь элементы этих множеств на диаграмме Венна. Сделай вывод.
ачнём с № 2 стр. 27. Прочитайте задание.(Работает у доски Шнурков Даниил), остальные учащиеся работают в учебнике)
Перечислите элементы множества А. (А = {1; 2; 3; 4}.)
Перечислите элементы множества В. (В = {3; 4; 5}.)
Какие элементы являются общей частью множеств А и В, В и А? (Элементы 3 и 4.)
Запишите элементы множеств А и В и отметьте их на диаграмме. (А ∩ В = {3; 4},
В ∩ А = {3;4}.)
Докажите. (Пересечение множеств не зависит от порядка множеств.)
2) № 3, стр. 27
Прочитайте задание. (Работает у доски Курашов Андрей, остальные учащиеся работают в учебнике)
Чем отличаются записи (А ∩ В) ∩ С = А ∩ (В ∩ С)? (В первом случае сначала находится пересечение множеств А и В, затем его пересечение с множеством С. Во втором случае, наоборот, сначала находится В ∩ С, а затем его пересечение с А.)
– Какой вы сделайте вывод. (Пересечение множеств не зависит от порядка действий.)
6.Работа в парах с самопроверкой по эталону.
Цель:
1) организовать самостоятельное выполнение учащимися заданий на новые понятия;
2) организовать самооценку детьми правильность выполнения задания (при необходимости – коррекцию возможных ошибок).
На проекторе выражением: « ТОРОПИСЬ — ДА НЕ ОШИБИСЬ!»(СЛАЙД)
Как вы думаете, к какому виду деятельности подходит это выражение? (самостоятельная работа).
С какой целью мы выполняем эту работу? (Чтобы выяснить, как усвоили новые знания.)
– Перед вами задание №2.
Прочитайте внимательно задание и выполните его на листочках.
Задание:
Допишите равенства, выражающие переместительное и сочетательное свойства операции пересечения множеств:
М ∩ К =
(М ∩ К) ∩ Т =
(Слад)
М ∩ К = К ∩ М Пересечение множеств не зависит
от порядка множеств и порядка
(М ∩ К) ∩ Т = М ∩ (К ∩ Т) действий.
Проверка:
Поставьте знак «+», если вы выполнили так же «?» если по-другому.
Какие были затруднения? (…)
Исправьте ошибки.
7. Физкультминутка для глаз и дыхания .
8.Включение в систему знаний и повторение.
Цель:
1) тренировать вычислительные навыки через решение примеров с использованием свойств для сложения и умножения;
2) повторить решение задач на приведение к единице, составление и решение уравнений, порядок действий в выражениях со скобками;
3) проверить у дете?
