Назовите свойства равнобедренного треугольника какие из них
Содержание:
- Свойства равнобедренного треугольника.
- Признаки равнобедренного треугольника.
- Формулы равнобедренного треугольника:
- формулы длины стороны;
- формулы длины равных сторон;
- формулы высоты, медианы, биссектрисы равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.
АВ = ВС — боковые стороны
АС — основание
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника выражаются через 5 теорем:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Рассмотрим равнобедренный Δ ABC с основанием АС.
Боковые стороны равны АВ = ВС,
Следовательно углы при основании ∠ BАC = ∠ BСA.
Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника
- Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
- Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Доказательство теоремы:
- Дан Δ ABC.
- Из точки В проведем высоту BD.
- Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
- Прямые АС и BD называются перпендикуляром.
- В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).
- АВ = ВС — боковые стороны равны.
- Стороны АD = СD, т.к. точка D отрезок делит пополам.
- Следовательно Δ ABD = ΔBCD.
- Биссектриса, высота и медиана это один отрезок – BD
Вывод:
- Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
- Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
- Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.
Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.
- Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство теоремы:
Дано два Δ ABC и Δ A1B1C1. Стороны AB = A1B1; BC = B1C1; AC = A1C1.
Доказательство от противного.
- Пусть треугольники не равны (а то треугольники были равны по первому признаку).
- Пусть Δ A1B1C2 = Δ ABC, у которого вершина C2 лежит в одной полуплоскости с вершиной C1 относительно прямой A1B1. По предположению вершины C1 и C2 не совпадают. Пусть D – середина отрезка C1C2. Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
- Отсюда пришли к противоречию и теорему доказали.
Признаки равнобедренного треугольника
- Если в треугольнике два угла равны.
- Сумма углов треугольника 180°.
- Если в треугольнике биссектриса является медианой или высотой.
- Если в треугольнике медиана является биссектрисой или высотой.
- Если в треугольнике высота является медианой или биссектрисой.
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы длины стороны (основания — b):
- b = 2a sin( beta /2)= a sqrt { 2-2 cos beta }
- b = 2a cos alpha
Формулы длины равных сторон — (а):
- a=frac { b } { 2 sin(beta /2) } = frac { b } { sqrt { 2-2 cos beta } }
- a=frac { b } { 2 cosalpha }
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
- L — высота=биссектриса=медиана
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
- L = a sina
- L = frac { b } { 2 } *tgalpha
- L = a sqrt { (1 + cos beta)/2 } =a cos (beta)/2)
Формула высоты, биссектрисы и медианы, через стороны, (L):
- L = sqrt { a^ { 2 } -b^ { 2 } /4 }
Площадь равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- h — высота
Формула площади треугольника через высоту h и основание b, (S):
S=frac { 1 } { 2 } *bh
Смотри также:
- Теорема о сумме углов треугольника
- Формулы площади поверхности, основания, сечения призмы
- Площадь поверхности куба, формулы и примеры
- Основные формулы по математике
- Справочные материалы ЕГЭ от ФИПИ по математике
Источник
Равнобедренный треугольник имеет ряд свойств, которые отличают его от произвольной фигуры. Именно эти свойства во многом помогают решению задач, связанных с равнобедренным треугольником. В этой статье мы подробно разберем каждый из признаков, приведем доказательства и поговорим об обратных теоремах.

Теорема 1
В равнобедренном треугольнике углы при основании равны.
Это свойство углов равнобедренного треугольника можно легко и быстро доказать. Из вершины на основание опустим высоту BH. В результате получим два прямоугольных треугольника, у которых катет BH будет общим, а гипотенузы АВ и ВС равны между собой, так как являются боковыми сторонами равнобедренного треугольника.
Тогда треугольники АВН и ВСН равны по гипотенузе и катету.
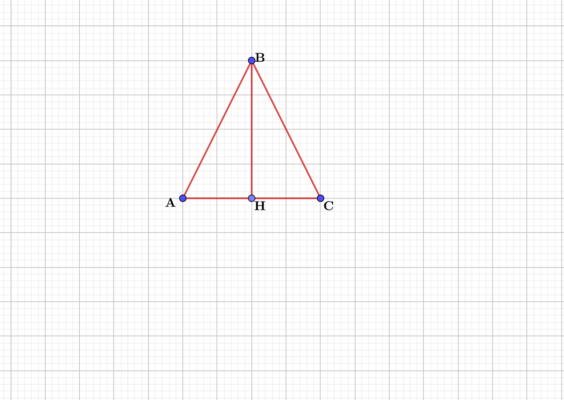
Рис. 1. Рисунок к доказательству
В работе с прямоугольными треугольниками полезны теоремы равенства, которые значительно упрощают доказательство. Любую из них можно вывести из 3 основных теорем равенств треугольников, но это занимает лишнее время, которое можно сэкономить, просто запомнив 5 признаков равенства прямоугольных треугольников.
Раз треугольники равны, то соответствующие элементы тоже равны, то есть угол ВАН и угол ВСН равны между собой. Что и требовалось доказать.
Теорема 2
Перед формулированием теоремы, нужно сказать, что теорем всего 4, но 2, 3 и 4 похожи между собой. Поэтому докажем только 2, а остальные просто сформулируем.
В равнобедренном треугольнике высота, проведенная к основанию, является так же биссектрисой и высотой.
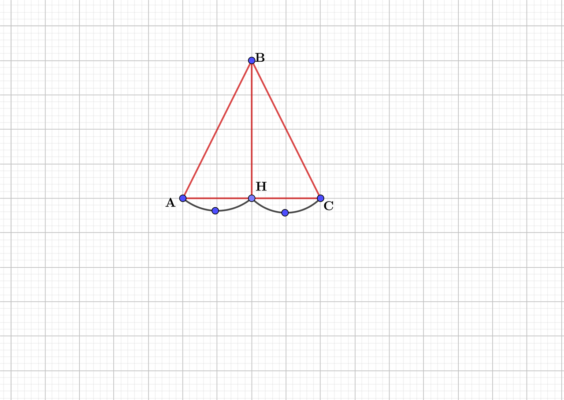
Рис. 2. Высота равнобедренного треугольника
Проведем в треугольнике АВС высоту ВН. Она разделить треугольник на два прямоугольных, которые будут равны между собой по гипотенузе и катету, так же, как и в доказательстве первой теоремы. Если треугольники равны, значит, соответственные элементы тоже равны.
Значит отрезок AH=HC. А это значит, что BH является медианой. Так как медиана, это отрезок, соединяющий вершину треугольника и середину противоположной стороны.
Углы АВН и НВС равны, а значит, отрезком ВН угол АВС делится пополам, т.е. ВН является его биссектрисой. Биссектриса это отрезок, который делит угол пополам.
Сформулируем и запишем краткое доказательство оставшихся двух теорем.
Теорема 3
Медиана, проведенная из вершины равнобедренного треугольника, является так же высотой и биссектрисой.
В этом случае ВН будет являться медианой. Тогда сторона ВН – общая для двух треугольников, стороны АВ=ВС – по определению равнобедренного треугольника, АН=НС, так как ВН является медианой. Значит, треугольники АВН и ВСН равны по трем сторонам. Дальнейшее доказательство совпадает с теоремой 2.
Теорема 4
Биссектриса, проведенная из вершины равнобедренного треугольника, является также медианой и высотой.
Тогда, угол АВН равен углу НВС по определению биссектрисы, сторона ВН – общая, а стороны АВ=ВС – по определению. Треугольники АВН и ВСН равны по двум сторонам и углу между ними.
Как видно, теоремы говорят об одном и том же, а также имеют схожие доказательства, поэтому очень часто запоминают лишь вторую теорему, приводя ее в решении и пользуясь, при этом, всеми тремя. Подобные рассуждения ошибкой не являются.
Теорема, обратная теореме 1
Теоремы, обратные теоремам 2, 3 и 4 не имеют смысла, так как будут повторять друг друга. Но теорема, обратная теореме 1, является одним из признаков равнобедренного треугольника, поэтому может использоваться при решении.
Формулировка: Если в треугольнике два угла равны между собой, то такой треугольник является равнобедренным.
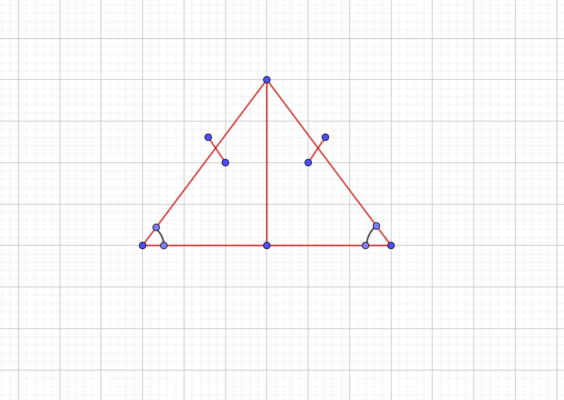
Рис. 3. Иллюстрация признака
Это нужно учитывать, поскольку в задаче не всегда определяют вид треугольника, а без использования свойств в задачах на эту тему не обойтись.
Что мы узнали?
Мы разобрали 4 теоремы о свойствах равнобедренного треугольника, сформулировали обратную теорему и разобрались в доказательствах свойств. Сказали, что эти свойства характерны только для равнобедренного треугольника и использовать их для произвольной фигуры нельзя, а также разобрались в том, как просто и быстро запомнить каждое из свойств.
Тест по теме
Оценка статьи
Средняя оценка: 4.2. Всего получено оценок: 141.
Источник
Понятие равнобедренного треугольника
Введем для начала определение треугольника.
Выберем на плоскости три произвольные точки, которые будут удовлетворять условию аксиомы 1. Соединим эти точки между собой отрезками. Тогда
Определение 1
Треугольником будем называть такую геометрическую фигуру, которая состоит из трех точек, не имеющих общей прямой, соединенных отрезками.
Определение 2
Точки в рамках определения 1 называются вершинами треугольника.
Определение 3
Отрезки в рамках определения 1 называются сторонами треугольника.
Введем теперь понятие равнобедренного треугольника.
Определение 4
Треугольник будем называть равнобедренным, если две его стороны будут равны между собой.
Определение 5
Равные стороны в рамках определения 4, будем называть боковыми, а третью – основанием (рис. 1).
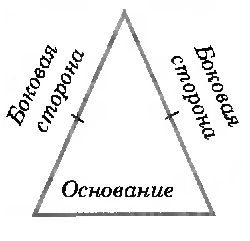
Замечание 1
Отметим, что если боковые стороны равнобедренного треугольника также равняются его основанию, то треугольник будем называть равносторонним.
Свойства равнобедренного треугольника
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Введем свойства равнобедренного треугольника в виде теорем.
Теорема 1
Углы при основании равнобедренного треугольника будут равными.
Доказательство.
Пусть нам дан треугольник $ABC$, в котором $AB=AC$. Проведем биссектрису $AD$ к основанию данного нам треугольника (рис. 2).
Так как $AD$ – биссектриса, то будет верно равенство
$∠1=∠2$
Для треугольников $ABD$ и $ACD$ сторона $AD$ является общей. Следовательно, треугольники $ABD$ и $ACD$ равны по первому признаку. Но тогда будет верно, что
$∠B=∠C$
Теорема доказана.
Замечание 2
Из этой теоремы можно выделить признак равнобедренности треугольника. Если в треугольнике будут иметься два равных угла, то он будет являться равнобедренным.
Теорема 2
Высота, медиана и биссектриса в равнобедренном треугольнике являются одной и той же прямой.
Доказательство.
Пусть нам дан треугольник $ABC$, в котором $AB=AC$. Проведем биссектрису $AD$ к основанию данного нам треугольника (рис. 3). Докажем, для начала, что $AD$ является медианой.
Так как $AD$ – биссектриса, то будет верно равенство
$∠1=∠2$
Для треугольников $ABD$ и $ACD$ сторона $AD$ является общей. Следовательно, треугольники $ABD$ и $ACD$ равны по первому признаку. Но тогда верно, что $BD=DC$. Следовательно, $AD$ – медиана.
Докажем теперь, что $AD$ – высота. Введем следующие обозначения. Пусть $∠1=α$, $∠B=β$.
Так как $AD$ – биссектриса, то $∠A=2α$.
По теореме о сумме углов в треугольнике, из треугольника $ABC$ будем иметь
$∠A+∠B+∠C=180^0$
То есть
$2α+2β=180^0$
$α+β=90^0$
Из треугольника $ABD$ будем иметь
$∠BDA+α+β=180^0$
Тогда
$∠BDA=180^0-(α+β)=180^0-90^0=90^0$
Следовательно, $AD$ – высота.
Теорема доказана.
Пример задач
Пример 1
Пусть дан треугольник $ABC$. Доказать, что если в нем $BD$ будет и высотой и медианой, то треугольник является равнобедренным.
Доказательство.
Для этого нам нужно доказать, что $AB=BC$.
Изобразим рисунок по условию задачи (рис. 4).
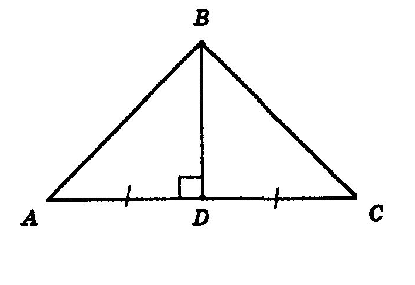
Так как $BD$ является медианой, то по определению 4 будет верно равенство
$AD=DC$
Так как $BD$ является высотой, то по определению 6 будет верно равенство
$∠ADB=∠BDC=90^0$
У треугольников $ADB$ и $BDC$ сторона $BD$ будет общей, следовательно, по всему сказанному выше эти треугольники равняются по первому признаку. Но тогда и стороны $AB$ и $BC$ равны.
Пример 2
Пусть дан треугольник $ABC$. Доказать, что он будет равнобедренным в условиях рисунка 5.
Доказательство.
По условию задачи угол 1 равняется углу 2, а сторона $BD$ равняется стороне $CD$. Так как у треугольников $ADB$ и $ADC$ сторона $AD$ является общей, то треугольники $ADB$ и $ADC$ будут равняться по первому признаку. Но тогда и стороны $AB$ и $AC$ также равны между собой. Следовательно, данный треугольник будет равнобедренным.
Источник
Свойства равнобедренного треугольника выражают следующие теоремы.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Докажем одну из них, например теорему 2.5.
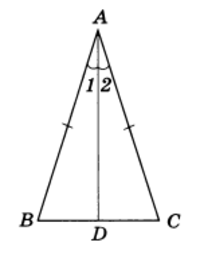
Рис.1
Доказательство. Рассмотрим равнобедренный треугольник ABC с основанием ВС и докажем, что ∠ В = ∠ С. Пусть AD — биссектриса треугольника ABC (рис.1). Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD — общая сторона, ∠ 1 = ∠ 2, так как AD — биссектриса). Из равенства этих треугольников следует, что ∠ В = ∠ С. Теорема доказана.
С использованием теоремы 1 устанавливается следующая теорема.
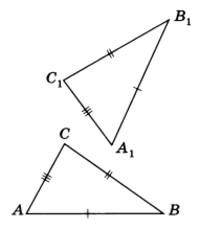
Рис.2
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны (рис. 2).
Замечание. Предложения, установленные в примерах 1 и 2, выражают свойства серединного перпендикуляра к отрезку. Из этих предложений следует, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Пример 1. Доказать, что точка плоскости, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Решение. Пусть точка М равноудалена от концов отрезка АВ (рис. 3), т. е. AM = ВМ.
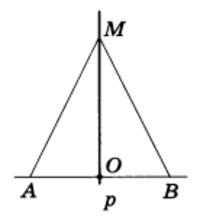
Рис.3
Тогда Δ АМВ равнобедренный. Проведем через точку М и середину О отрезка АВ прямую р. Отрезок МО по построению есть медиана равнобедренного треугольника АМВ, а следовательно (теорема 3), и высота, т. е. прямая МО, есть серединный перпендикуляр к отрезку АВ.
Пример 2. Доказать, что каждая точка серединного перпендикуляра к отрезку равноудалена от его концов.
Решение. Пусть р — серединный перпендикуляр к отрезку АВ и точка О — середина отрезка АВ (см. рис. 3).

Рис.3
Рассмотрим произвольную точку М, лежащую на прямой р. Проведем отрезки AM и ВМ. Треугольники АОМ и ВОМ равны, так как у них углы при вершине О прямые, катет ОМ общий, а катет ОА равен катету ОВ по условию. Из равенства треугольников АОМ и ВОМ следует, что AM = ВМ.
Пример 3. В треугольнике ABC (см. рис. 4) АВ = 10 см, ВС = 9 см, АС = 7 см; в треугольнике DEF DE = 7 см, EF = 10 см, FD = 9 см.
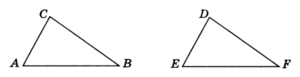
Рис.4
Сравнить треугольники ABC и DEF. Найти соответственно равные углы.
Решение. Данные треугольники равны по третьему признаку. Соответственно равные углы: А и Е (лежат против равных сторон ВС и FD), В и F (лежат против равных сторон АС и DE), С и D (лежат против равных сторон АВ и EF).
Пример 4. На рисунке 5 АВ = DC, ВС = AD, ∠B = 100°.
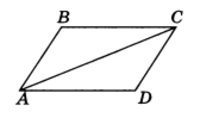
Рис.5
Найти угол D.
Решение. Рассмотрим треугольники ABC и ADC. Они равны по третьему признаку (АВ = DC, ВС = AD по условию и сторона АС — общая). Из равенства этих треугольников следует, что ∠ В = ∠ D, но угол В равен 100°, значит, и угол D равен 100°.
Пример 5. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC . Ответ дайте в градусах.
Видео-решение.

Источник
Среди всех треугольников есть два особенных вида: прямоугольные и равнобедренные.
Чем же эти виды треугольников такие уж особенные?
Ну, во-первых, такие треугольники чрезвычайно часто оказываются главными «действующими лицами» задач ЕГЭ первой части.
А во-вторых, задачи про прямоугольные и равнобедренные треугольники решаются гораздо легче, чем другие задачи по геометрии.
Нужно всего лишь знать несколько правил и свойств. Все самое интересное о прямоугольных треугольниках обсуждается в соответствующей теме, а сейчас рассмотрим равнобедренные треугольники.
И, прежде всего, что же такое равнобедренный треугольник.
Поехали!
НАЧАЛЬНЫЙ УРОВЕНЬ
Определение равнобедренного треугольника
Треугольник называется равнобедренным, если у него есть две равные стороны.
Посмотри, как это выглядит:
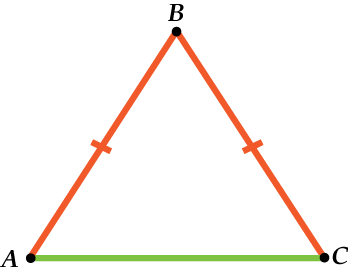
Как и у прямоугольного треугольника, у равнобедренного треугольника есть специальные названия для сторон.
Две равные стороны называются боковыми сторонами, а третья сторона –основанием.
И снова внимание на картинку:
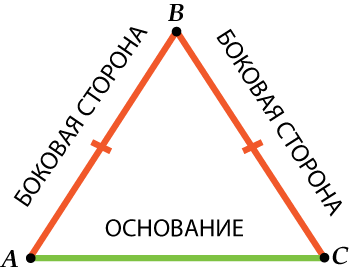
Может быть, конечно, и так:
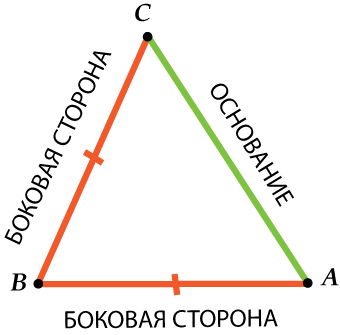
Так что будь внимательным: боковая сторона – одна из двух равных сторон в равнобедренном треугольнике, а основание – третья сторона.
Чем же так уж хорош равнобедренный треугольник?
Чтобы это понять, давай проведём высоту к основанию. Ты помнишь, что такое высота?
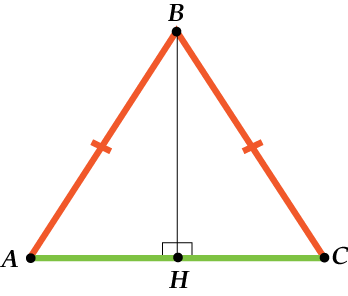
Это просто линия, проведённая из вершины треугольника перпендикулярно противоположной стороне.
Итак, провели высоту.
Что же получилось?
Из одного равнобедренного треугольника получилось два прямоугольных.
Это уже хорошо, но так получится в любом, даже самом «кособедренном» треугольнике.
Смотри:
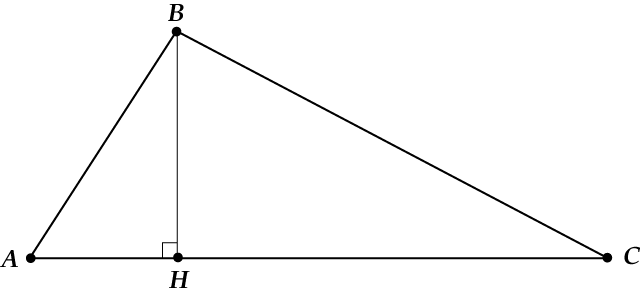
Тоже два прямоугольных….
Чем же отличается картинка для равнобедренного треугольника? Смотри ещё раз:
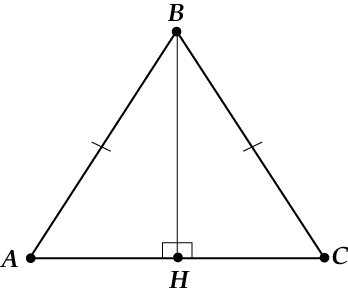
Видишь, два прямоугольных треугольника (( displaystyle Delta ABH) и ( displaystyle Delta CBH)) – одинаковые!
Или, как математически любят говорить? Равные!
Ну, во-первых, конечно, этим странным математикам мало просто видеть – нужно непременно доказывать. А то вдруг эти треугольники чуть-чуть разные, а мы будем считать их одинаковыми.
Но не переживай: в данном случае доказывать почти так же просто, как и видеть.
Начнём? Посмотри внимательно, у нас есть:
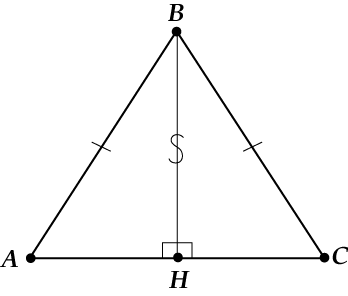
( displaystyle underbrace{AB}_{гипотенуза в Delta ABH}=underbrace{BC}_{гипотенуза в Delta СBH})
( displaystyle BHtext{ }=text{ }BH) (ещё говорят, ( displaystyle BH)- общая)
И, значит, ( displaystyle AHtext{ }=text{ }CH)! Почему? Да мы просто найдём и ( displaystyle AH), и ( displaystyle CH) из теоремы Пифагора (помня ещё при этом, что ( displaystyle AB=BC))
( displaystyle AH=sqrt{A{{B}^{2}}-B{{H}^{2}}})
( displaystyle CH=sqrt{B{{C}^{2}}-B{{H}^{2}}})
Удостоверились? Ну вот, теперь у нас
( displaystyle begin{array}{l}AB=BC\BH=BH\AH=CHend{array})
А уж по трём сторонам – самый легкий (третий) признак равенства треугольников.
Ну вот, наш равнобедренный треугольник разделился на два одинаковых прямоугольных.
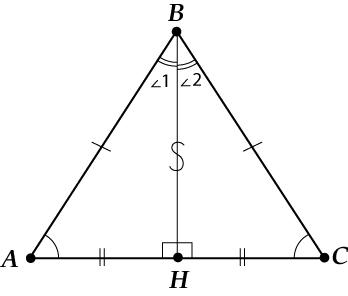
Отметим на картинке все одинаковые элементы (углы и стороны).
Видишь, как интересно? Получилось, что:
( displaystyle begin{array}{l}angle A=angle C\AH=CH\angle 1=angle 2end{array})
Как же об этом принято говорить у математиков? Давай по порядку:
- В равнобедренном треугольнике углы при основании равны
( displaystyle angle A=angle C); - Высота, проведенная к основанию, совпадает с медианой и биссектрисой.
( displaystyle AH=CH)
( displaystyle angle 1=angle 2).
(Вспоминаем тут, что медиана – линия, проведённая из вершины, которая делит сторону пополам, а биссектриса – угол.)
Ну вот, здесь мы обсудили, что хорошего можно увидеть, если дан равнобедренный треугольник. Мы вывели, что у равнобедренного треугольника углы при основании равны, а высота, биссектриса и медиана, проведенные к основанию, совпадают.
И теперь возникает другой вопрос: а как узнать, равнобедренный ли треугольник?
То есть, как говорят математики, каковыпризнаки равнобедренного треугольника?
И оказывается, что нужно просто «перевернуть» все высказывания наоборот. Так, конечно, не всегда бывает, но равнобедренный треугольник всё-таки отличная штука! Что же получится после «переворачивания»?
I. Если в каком-то треугольнике есть два равных угла, то такой треугольник – равнобедренный (ну и естественно, углы эти окажутся при основании).
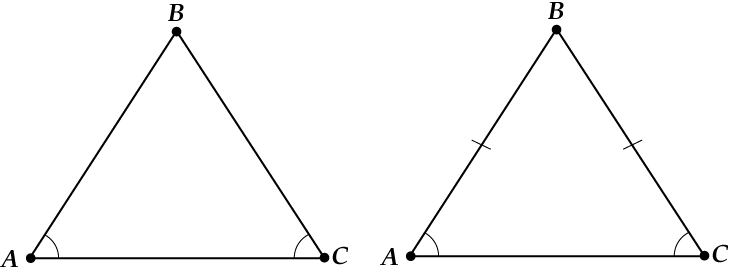
II. Если в каком-то треугольнике
- высота и медиана или
- высота и биссектриса или
- биссектриса и медиана,
проведённые к какой-то стороне, совпадут, то такой треугольник – равнобедренный, а сторона эта – основание.
Ну вот смотри:
Если совпадают высота и медиана, то:
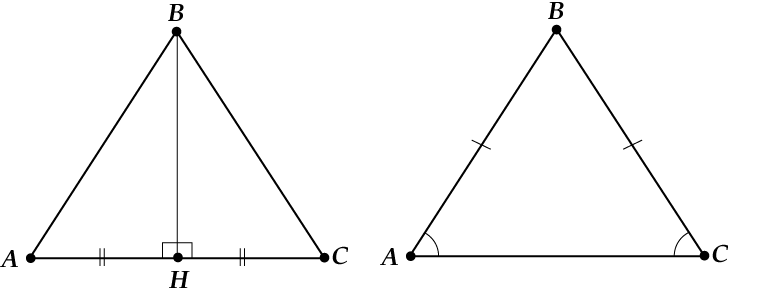
Если совпадают высота и биссектриса, то:
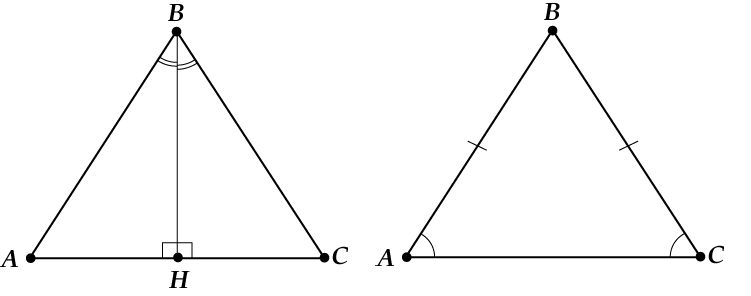
Если совпадают биссектриса и медиана, то:
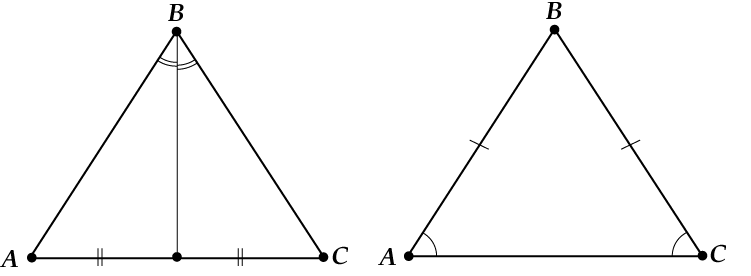
Ну вот, не забывай и пользуйся:
- Если дан равнобедренный треугольный треугольник, смело проводи высоту, получай два прямоугольных треугольника и решай задачу уже про прямоугольный треугольник;
- Если дано, что два угла равны, то треугольник точно равнобедренный и можно проводить высоту и ….( Дом, который построил Джек… ???? );
- Если оказалось, что высота разделила сторону пополам, то треугольник – равнобедренный со всеми вытекающими бонусами;
- Если оказалось, что высота разделила угол полам – тоже равнобедренный;
- Если биссектриса разделила сторону пополам или медиана – угол, то это тоже бывает только в равнобедренном треугольнике.
Давай посмотрим, как это выглядит в задачах.
В треугольнике ( displaystyle ABC) стороны ( displaystyle AB) и ( displaystyle AC) равны, а ( displaystyle angle BAC=70{}^circ ).
Найти ( displaystyle angle ABC).
Решаем:
Сначала рисунок.
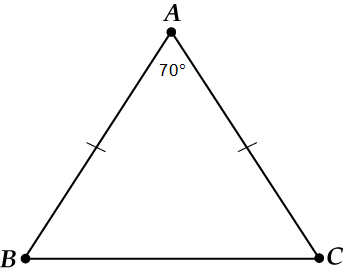
Что здесь основание? Конечно, ( displaystyle BC).
Вспоминаем, что если ( displaystyle AB=AC), то и ( displaystyle angle B=angle C).
Обновлённый рисунок:
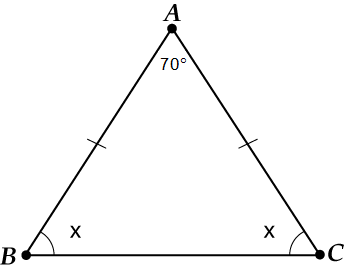
Обозначим ( displaystyle angle B) за ( displaystyle x). Чему там равна сумма углов треугольника? ( displaystyle 180{}^circ )?
Пользуемся:
( displaystyle 70{}^circ +x+x=180{}^circ )
( displaystyle 2x=110{}^circ )
( displaystyle x=55{}^circ )
Вот иответ: ( displaystyle angle ABC=55{}^circ ).
Несложно, правда? Даже высоту проводить не пришлось.
(Тоже не очень хитрая, но нужно повторить тему «Прямоугольный треугольник»)
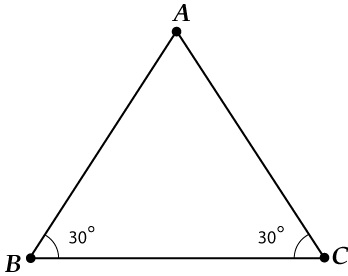
В треугольнике ( displaystyle ABC) ( displaystyle angle B=angle C=30{}^circ ), ( displaystyle BC=24sqrt{3}).
Найти ( displaystyle AB).
Решаем:

Смотрим внимательно и соображаем, что раз ( displaystyle angle B=angle C), то ( displaystyle AB=AC).
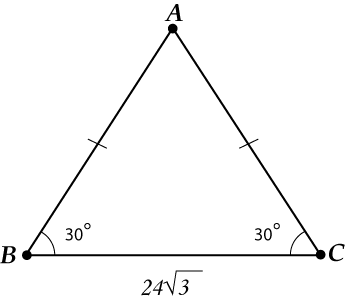
Треугольник-то равнобедренный! Проводим высоту (это и есть фокус, с помощью которого сейчас все решится).
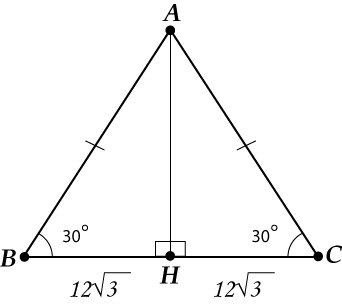
Вспоминаем, что высота = медиана, то есть
( BH=HC=12sqrt{3}).
Теперь «вычёркиваем из жизни» ( displaystyle Delta AHC), рассмотрим только ( displaystyle Delta ABH).
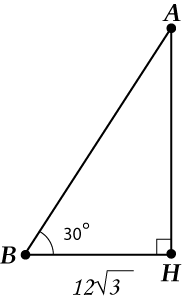
Итак, в ( displaystyle Delta ABH) имеем: ( cos 30{}^circ =frac{12sqrt{3}}{AB})
Вспоминаем табличные значения косинусов (ну, или глядим в шпаргалку…
( frac{sqrt{3}}{2}=frac{12sqrt{3}}{AB})
Осталось найти ( AB): ( AB=frac{12sqrt{3}cdot 2}{sqrt{3}}=24).
Ответ: ( displaystyle AB=24).
Заметим, что нам тут очень потребовались знания, касающиеся прямоугольного треугольника и «табличных» синусов и косинусов.
Очень часто так и бывает: темы «Прямоугольный треугольник», «Равнобедренный треугольник» и «Основные формулы тригонометрии» в задачках ходят в связках, а с другими темами не слишком дружат.
Треугольник называется равнобедренным, если у него есть две равные стороны.
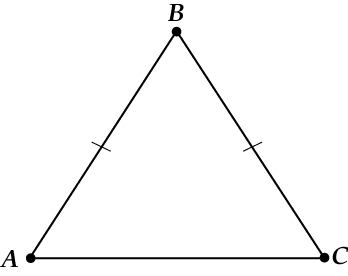
Эти две равные стороны называются боковыми сторонами, а третья сторона – основание равнобедренного треугольника.
Посмотри на рисунок: ( displaystyle AB) и ( displaystyle BC) – боковые стороны, ( displaystyle AC) – основание равнобедренного треугольника.
