На каком свойстве прямых основан этот способ проверки правильности линейки

№ 1.

1) Проведите прямую. Отметьте какую-нибудь точку А, лежащую на прямой, и точку В, не лежащую на прямой.

2) Проведите две пересекающиеся прямые А и B. Отметьте точку С пересечения прямых: точку А на прямой А, не лежащую на прямой B; точку D, не лежащую ни на одной из прямых A и B[I].

№ 2.

Отметьте на листе бумаги две точки. Проведите через них от руки прямую. С помощью линейки проверьте правильность построения.

№ 3.

Могут ли две прямые иметь две точки пересечения?

Задача решена в п. 2 учебника (стр. 4).

№ 4.

Для проверки правильности линейки применяют такой способ. Через две точки с помощью линейки проводят линию. Затем линейку переворачивают и через те же точки снова проводят линию. Если линии не совпадают, то линейка неправильная. На каком свойстве прямых основан этот способ проверки правильности линейки?

Этот способ проверки правильности линейки основан на том, что через две точки можно провести единственную прямую.

№ 5.

Проведите прямую А. Отметьте на прямой две какие-нибудь точки А и В. Отметьте теперь точку С так, чтобы точка А лежала между точками В и С.

№ 6.

Проведите прямую А. Отметьте на прямой две какие-нибудь точки А и В. Отметьте теперь какую-нибудь точку С отрезка АВ.

№ 7.

Точка М лежит на прямой CD между точками С и D. Найдите длину отрезка CD, если

1) СМ = 2,5 см, MD = 3,5 см;

2) СМ = 3,1 дм, MD = 4,6 дм;

3) СМ = = 12,3 м, MD = 5,8 м.

По условию точка М лежит между двумя точками С и D, по свойству измерения отрезков получаем CD = CM + MD.

1) CD = 2,5 см + 3,5 см = 6 см;

2) CD = 3,1 дм + 4,6 дм = 7,7 дм;

3) CD = 12,3 м + 5,8 м = 18,1 м.

Ответ: 1) 6 см;

2) 7,7 дм;

3) 18,1 м.

№ 9.

Три точки А, В, С лежат на одной прямой. Известно, что АВ = 4,3 см АС = 7,5 см, ВС = 3,2 см. Может ли точка А лежать между точками В и С? Может ли точка С лежать между точками А и В? Какая из трех точек А, В, С лежит между двумя другими?

Задача решена в п. 4 учебника (стр. 6).

№ 10.

Точки А, В, С лежат на одной прямой. Принадлежит ли точка В отрезку АС, если АС = 5 см, ВС = 7 см? Объясните ответ.

Если точка В принадлежит отрезку АС, значит, лежит между точками А и С, по свойству измерения отрезков получаем АВ + ВС = АС, следовательно, АВ + 7 см = 5 см, но это невозможно. Значит предположение неверно, и точка В не принадлежит отрезку АС.

Ответ: Точка В не принадлежит отрезку АС.

№ 11.

Точки А, В, С лежат на одной прямой. Может ли точка В разделять точки А и С, если АС = 7 м, ВС = 7,6 м? Объясните ответ.

Предположим, точка В разделяет точки А и С, а, значит, лежит между ними, тогда по свойству измерения отрезков получаем: АВ + ВС = АС, следовательно, АВ + 7,6 м = 7 м, что невозможно. Значит, точка В не разделяет точки А и С.

Ответ: Точка В не может разделять точки А и С.

№ 12.

Могут ли точки А, В, С лежать на одной прямой, если АВ = 1,8 м, АС = 1,3 м, ВС = 3 м? Объясните ответ.

Пусть точки А, В, С лежат на одной прямой, тогда одна из них находится между двумя другими точками, и по свойству измерения отрезков получаем:

1) ВС = АВ + АС, что неверно, т. к. 3 м ≠ 1,8 м + 1,3 м;

2) АВ = АС + СВ, что неверно, т. к. 1,8 м ≠ 1,3 м + 3 м.

3) АС = АВ + ВС, что неверно, т. к. 1,3 м ≠ 1,8 м + 3 м;

Значит:

1) Точка В не лежит между точками А и С.

2) Точка А не лежит между точками В и С.

3) Точка С не лежит между точками А и В.

Ответ: Точки А, В, С не могут лежать на одной прямой.

№ 13.

Могут ли три точки А, В, С лежать на одной прямой, если длина большего отрезка АВ меньше суммы длин отрезков АС и ВС? Объясните ответ.

Три точки А, В, С лежат на одной прямой, если АВ = АС + СВ (по свойству измерения отрезков), а по условию AB < АС + СВ, значит, точки А, В, С не могут лежать на одной прямой.

Ответ: Точки А, В, С не могут лежать на одной прямой.

№ 14.

Точки А, В, С лежат на одной прямой. Найдите длину отрезка ВС, если АВ = 2,7 м, АС = 3,2 м. Сколько решений имеет задача?

Существуют два решения.

1) Если точка А лежит между В и С, тогда ВС = АВ + АС = 2,7 м + 3,2 м = 5,9 м.

2) Если точка В лежит между А и С, тогда

ВС = АС — АВ = 3,2 м — 2,7 м = 0,5 м.

Ответ: 5,9 м или 0,5 м.

№ 15.

На отрезке АВ длиной 15 м отмечена точка С. Найдите длины отрезков АС и ВС, если:

1) отрезок АС на 3 м длиннее отрезка ВС;

2) отрезок АС в два раза длиннее отрезка ВС;

3) точка С — середина отрезка АВ;

4) длины отрезков АС и ВС относятся как 2:3.

Ответ: 1) АС = 9 м, ВС = 6 м;

2) АС = 10 м, ВС = 5 м;

3) АС = 7,5 м, ВС = 7,5 м;

4) АС = 6 м, ВС = 9 м.

№ 16.

Проведите прямую и отметьте какую-нибудь точку А, не лежащую на этой прямой. Отметьте теперь две точки В и С так,

Чтобы отрезок АВ пересекал прямую, а отрезок ВС не пересекал ее.

№ 17.

Дана прямая и три точки А, В, С, не лежащие на этой прямой. Известно, что отрезок АВ пересекает прямую, а отрезок АС не пересекает ее. Пересекает ли прямую отрезок ВС? Объясните ответ.

Задача решена в п. 5 учебника (стр. 7).

№ 18.

Даны прямая и четыре точки А, В, С и D, не лежащие на этой прямой. Пересекает ли прямую отрезок AD, если:

1) отрезки АВ, ВС и CD пересекают прямую;

2) отрезки АС и ВС пересекают прямую, а отрезок BD

Не пересекает;

3) отрезки АВ и CD пересекают прямую, а отрезок ВС не пересекает;

4) отрезки АВ и CD не пересекают прямую, а отрезок ВС пересекает;

5) отрезки АВ, ВС, CD не пересекают прямую;

6) отрезки АС, ВС и BD пересекают прямую? Объясни

Те ответ.

Плоскость разделяется прямой на две полуплоскости. Отрезок AD пересекают нашу прямую, если концы отрезка — А и D— лежат в разных полуплоскостях.

1) а) АВ пересекает А, следовательно, А и В лежат в разных полуплоскостях относительно А. Аналогично: В и С лежат в разных полуплоскостях относительно А. Следовательно, А и С Лежат в одной полуплоскости относительно А.

Б) AD пересекает А, следовательно, А и D лежат в разных полуплоскостях относительно А.

Из а) и б) следует, что С и D лежат в разных полуплоскостях

Относительно А, следовательно, CD пересекает А.

Аналогично 2), 3), 4), 5), 6).

Ответ: 1) пересекает;

2) не пересекает;

3) не пересекает;

4) пересекает;

5) не пересекает;

6) пересекает.

№ 19.

Даны пять точек и прямая, не проходящая ни через одну из этих точек. Известно, что три точки расположены в одной полуплоскости относительно этой прямой, а две точки — в другой. Каждая пара точек соединена отрезком. Сколько отрезков пересекает прямую? Объясните ответ.

6 отрезков: AD; AN; BD; BN; CD; CN.

Отрезок пересекает прямую тогда и только тогда, когда концы отрезка принадлежат разным полуплоскостям.

№ 20.

Даны прямая A и точки А, X, У, Z на этой прямой. Известно, что точки X, У лежат по одну сторону от точки А, точки X и Z тоже лежат по одну сторону от точки А. Как расположены точки У и Z относительно точки А : по одну сторону или по разные стороны? Объясните ответ.

Задача решена в п. 6 учебника (стр. 7).

№ 21.

Отметьте две точки А и В. Проведите полупрямую АВ.

№ 22.

На отрезке АВ взята точка С. Среди полупрямых АВ, АС, СА, СВ назовите пары совпадающих полупрямых, дополнительных полупрямых. Объясните ответ.

Задача решена в п. 6 учебника (стр. 8).

№ 24.

Луч а проходит между сторонами угла (cd). Найдите угол (cd), если

1) ∠(ac) = 35°, ∠(ad) = 75°;

2) ∠(ac) = = 57°, ∠(ad) = 62°;

3) ∠(ac) = 94°, ∠(ad) = = 85°.

Если угол разбивается на углы любыл лучом, проходящим между его сторонами через его вершину, то градусная мера угла равна сумме градусных мер этих углов, значит, ∠(Cd) = ∠(Ac) + ∠(Ad).

1) ∠(Cd) = 35o + 75o = 110o;

2) ∠(Cd) = 57o + 62o = 119o;

3) ∠(Cd) = 94o + 85o = 179o.

Ответ:1) 110о;

2) 119о;

3) 179о.

№ 25.

Может ли луч С проходить между сторонами угла (ab), если

1) ∠(ac) = 30°, ∠(cb) = 80°, ∠(ab) = 50°;

2) ∠(ac) = = 100°, ∠(cb) = 90°;

3) угол (ас) больше угла (ab)?

Задача решена в п. 7 учебника (стр. 9).

№ 26.

Между сторонами угла (ab), равного 60°, проходит луч C. Найдите углы (ос) и (bc), если

1) угол (ас) на 30° больше угла (Ьс);

2) угол (ас) в два раза больше угла (Ьс);

3) луч C делит угол (ab) пополам;

4) градусные меры углов (ас) и (Ьс) относятся как 2:3.

Поскольку луч С проходит между сторонами угла (Ab), по свойству измерения углов получаем:

∠(ac) + ∠(bc) = ∠(ab).

1) ∠(Ab) = ∠(Bc) + ∠(Bc) + 30o,

60o = 2 ∙ ∠(bc) + 30o;

2 ∙ ∠(bc) = 30o;

∠(Ac) = 45o, ∠(Bc) = 15о.

2) ∠(ab) = 2 ∙ ∠(bc) + ∠(bc),

60o = 3 ∙ ∠(Bc),

∠(Ac) = 40o, ∠(Bc) = 20о.

3) ∠(Ac) = ∠(Bc) = ∠(Ab) : 2 = 60o : 2 = 30o.

4) ∠(Ac) = 2X, ∠(Bc) = 3X, ∠(Ab) = 60o,

2X + 3Х = 60о,

5Х = 60о, Х = 12о.

∠(Ac) = 24о, ∠(Bc) = 36о.

Ответ: 1) ∠(Ac) = 45o, ∠(Bc) = 15o;

2) ∠(Ac) = 40o, ∠(Bc) = 20o;

3) ∠(Ac) = 30o, ∠(Bc) = 60o;

4) ∠(Ac) = 24o, ∠(Bc) = 36o.

№ 29.

Существует ли на полупрямой АВ такая точка X, отличная от В, что АХ = АВ? Объясните ответ.

Предположим, такая точка Х существует, Х ≠ В.

По свойству откладывания отрезков на любой полупрямой

Можно отложить единственный отрезок заданной длины от ее начальной точки. Следовательно, точки Х и В совпадут, т. е. Х =

В, что неверно по предположению, значит такой точки Х не существует.

№ 30.

На луче АВ отложен отрезок АС, меньший отрезка АВ. Какая из трех точек А, В, С лежит между двумя другими? Объясните ответ.

Задача решена в п. 8 учебника (стр. 10).

№ 31.

На луче АВ отмечена точка С. Найдите длину отрезка ВС, если:

1) АВ = 1,5 м, АС = 0,3 м;

2) АВ = 2 см, АС = 4,4 см.

Л C В

*— T — ■ —

ВС = АВ — АС = 1,5 м — 0,3 м = 1,2 м; 2)

ABC

ВС = АС — АВ = 4,4 см — 2 см = 2.4 см.

Ответ: 1) 1,2 м;

2) 2,4 см.

№ 33.

На стороне АВ треугольника АВС взята точка D. Чему равна сторона АВ треугольника, если AD = 5 см, а BD = 6 см?

AB = AD + BD = 5 см + 6 см = 11 см.

№ 34.

На стороне АВ треугольника АВС взята точка D. Найдите угол С треугольника, если ∠ACD = 30°, а ∠BCD = 70°.

По свойству измерения углов получим:

∠BCA = ∠ACD + ∠BCD = 30o + 70o = 100o.

Ответ: ∠BCA = 100o.

№ 36.

Треугольники АВС и PQR равны. Известно, что АВ = 5 см, ВС = б см, АС = 7 см. Найдите стороны треугольника PQR. Объясните ответ.

По условию треугольники АВС и PQR равны, значит, равны и их соответствующие стороны, тогда, AC = PR, АВ = PQ, BC = QR.

Получим: PQ = 5 см, PR = 7 см, QR = 6 см.

Ответ: PQ = 5 см, PR = 7 см, QR = 6 см.

№ 37.

Треугольники АВС и PQR равны. Углы второго треугольника известны: ∠P = 40°, ∠Q = 60°, ∠R = 80°. Найдите углы треугольника АВС.

По условию треугольники АВС и PQR равны, значит, у них равны и соответствующие углы, получаем:

∠B = ∠Q, ∠C = ∠R, ∠A = ∠P.

Следовательно, ∠C = 80o, ∠B = 60o, ∠A = 40o.

Ответ: ∠C = 80o, ∠B = 60o, ∠A = 40o.

№ 38.

Треугольники АВС и PQR равны. Известно, что cτopoHa АВ равна 10 м, а угол С равен 90°. Чему равны сторона PQ и угол R? Объясните ответ.

Задача решена в п. 9 учебника (стр. 12).

№ 39.

Треугольники АВС, PQR и XYZ равны. Известно, что АВ=5 см, QR=6 см, ZX=7 см. Найдите остальные стороны каждого треугольника.

По условию треугольники АВС, PQR и XYZ равны, значит, у них:

АВ = PQ = XY, значит, PQ = XY = 5 см;

СА = RP = ZX, значит, СА = RP = 7 см;

ВС = QR = YZ, значит, ВС = YZ = 6 см;

Ответ: PQ = 5 см, XY = 5 см, СА = 7 см, RP = 7 см,

ВС = 6 см, YZ = 6 см.

№ 40.

Дан треугольник АВС. Существует ли другой, равный ему треугольник ABD?

Из основного свойства простейших фигур, существует равный ему треугольник относительно данной полупрямой. Чтобы его найти, достаточно построить точку D, симмитричную точке С относительно прямой и соединить ее с точками А и В.

Ответ: существует.

№ 41.

Может ли прямая, пересекающая одну из двух параллельных прямых, не пересекать другую? Объясните ответ.

Задача решена в п. 11 учебника (стр. 13).

№ 42.

Даны две пересекающиеся прямые. Можно ли провести третью прямую, параллельную каждой из двух данных?

Пусть А — точка пересечения прямых А и B. Предположим, что мы провели прямую С, параллельную прямым А и B. Это значит, что через точку А проходят две прямые А и B, парал
лельные С, что противоречит аксиоме: через точку, не лежащую на прямой можно провести единственную прямую, паралель — ную данной.

Ответ: нельзя.

№ 43.

Может ли прямая, не проходящая ни через одну из вершин треугольника, пересекать каждую его сторону? Почему?

Не может.

По теореме: Если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон. Следовательно, не может.

№ 44*.

Даны четыре различные точки А, В, С и D. Известно, что точки А, В, С лежат на одной прямой и точки В, С, D также лежат на одной прямой. Докажите, что все четыре точки А, В, С, D лежат на одной прямой.

Прямые проходят через точки В и С. По аксиоме через любые две различные точки можно провести единственную прямую и получаем, что это одна и та же прямая. Так как она проходит через точки А, В, С и В, С, D, то все четыре точки А, В, С и D лежат на этой прямой. Что и требовалось доказать.

№ 45*.

Даны четыре прямые А, B, С и D. Известно, что прямые А, B, С Пересекаются в одной точке и прямые B, С, D также пересекаются в одной точке. Докажите, что все четыре данные прямые проходят через одну точку.

Прямые А, B, C пересекаются в одной точке, следовательно, прямая А проходит через точку пересечения прямых B и С. Прямые B, С, D пересекаются в одной точке, следовательно, прямая DПроходит через точку пересечения прямых B и C.

Две различные прямые не могут иметь двух точек пересечения, значит, прямые А и D проходят через одну точку пересечения прямых B и С, и, следовательно, все четыре прямые проходят через одну точку. Что и требовалось доказать.

№ 46*.

Точки А, В, С, D не лежат на одной прямой. Известно, что прямая АВ пересекает отрезок CD, а прямая CD пересекает отрезок АВ. Докажите, что отрезки АВ и CD пересекаются.

Прямая АВ пересекает отрезок CD, следовательно, точка пересечения прямых АВ и CD принадлежит отрезку CD.

Прямая CD пересекает отрезок АВ, следовательно, точка пересечения прямых АВ и CD принадлежит отрезку АВ.

Точка пересечения прямых АВ и CD принадлежит отрезку АВ И отрезку CD, получаем, что отрезки АВ и С D пересекаются в этой точке. Что и требовалось доказать.

№ 47*.

Дан треугольник АВС. На стороне АС взята точка B1 а на стороне ВС — точка A1. Докажите, что отрезки АА1 и ВВ1 пересекаются.

Прямая ВВ1 пересекает сторону АС в точке В1, следовательно, точки А и С располагаются в разных полуплоскостях относительно прямой ВВ1. Две прямые не могут иметь двух точек пересечения, следовательно, отрезок А1С не пересекает прямую ВВ1, и точки А1 и С лежат в одной полуплоскости относительно прямой ВВ1.

Так как точки А1 и С расположены в одной полуплоскости, а точки А и С — в разных полуплоскостях относительно прямой ВВ1, то точки А и А1 расположены в разных полуплоскостях, и следовательно отрезок АА1 пересекает прямую ВВ1.

Рассмотрим положение точек относительно прямой АА1. Точки В и С лежат в разных полуплоскостях, а точки В1 и С — в одной полуплоскости относительно прямой АА1. Значит, точки В и В1 лежат в разных полуплоскостях относительно прямой АА1 и следовательно отрезок ВВ1 пересекает прямую АА1.

Точка пересечения прямых АА1 и ВВ1 лежит и на отрезке АА1, и на отрезке ВВ1, следовательно, эти отрезки пересекаются. Что и требовалось доказать.

№ 48*.

Отрезки АВ и CD, не лежащие на одной прямой, пересекаются в точке Е. Докажите, что отрезок АС не пересекает прямую BD.

Две прямые не могут иметь двух точек пересечения, значит,

Отрезок ЕС не пересекает прямую DB, и точки Е и С лежат в одной полуплоскости относительно прямой DB.

Отрезок АЕ не пересекает прямую DB и точки А и Е лежат в одной полуплоскости относительно прямой DB.

Точки А и Е и точки С и Е лежат в одной полуплоскости относительно прямой DB, значит, точки А и С лежат в одной полуплоскости относительно прямой DB, и отрезок АС не пересекает прямую DB. Что и требовалось доказать.

№ 49*.

Докажите, что если луч, исходящий из вершины угла, пересекает отрезок АВ с концами на сторонах угла, то он пересекает

1) отрезок АС с концами на сторонах угла;

2) любой отрезок CD с концами на сторонах угла.

1) Пусть K — точка пересечения луча с отрезком АВ. Прямая OK пересекает отрезок АВ, следовательно, точки А и В лежат в разных полуплоскостях относительно прямой OK. Точки В и С Лежат в одной полуплоскости, так как отрезок ВС не пересекается с прямой OK, а точки А и С лежат в разных полуплоскостях, получаем, что прямая OK пересекает отрезок АС в некоторой точке, обозначим ее буквой Е.

Прямая ВС разбивает плоскость на две полуплоскости, в одной из которых лежит данный луч OK и точка А (поскольку отрезок AK не пересекает прямую ОВ) и точка Е (поскольку отрезок АЕ не пересекает прямую ОВ). Значит, точка Е должна лежать на луче OK.

2) Пусть CD — произвольный отрезок с концами на сторонах угла, и точка С лежит на стороне ОВ, а точка D на стороне ОА. Отрезок АВ пересекает луч OK, значит, луч OK пересекает и отрезок АС, а если луч пересекает АС, то луч будет пересекать и отрезок CD.

Что и требовалось доказать.

№ 50.

Докажите, что две прямые либо параллельны, либо пересекаются в одной точке.

Пусть даны две не параллельные прямые А и B, следовательно, они имеют общие точки. Если они имеют одну общую точку, то, это значит, что они пересекаются, если бы они имели две общие точки, то через эти точки проходили бы две различные прямые, что противоречит основному свойству принадлежности точек и прямых: через две различные точки можно провести прямую и притом только одну.

Что и требовалось доказать.

№ 51*.

Точки А и С принадлежат прямой а. На полупрямой СА отложен отрезок СВ, больший отрезка СА.

1) Какая из трех точек А, В, С лежит между двумя другими? Объясните ответ.

2) Докажите, что точка А разбивает прямую А на две полупрямые АВ и АС.

Точки А и В лежат на одной полупрямой с началом в точке С, следовательно, точка С не лежит между точками А и В.

Пусть В лежит между А и С, тогда АС = АВ + СВ и АС > СВ, что противоречит условию: СВ > АС, следовательно, В не лежит между точками А и С.

Из трех точек одна и только одна лежит между двумя другими. На основании предыдущих рассуждений приходим к выводу, что точка А лежит между точками В и С.

Через точку А проведем прямую B, отличную от прямой А. Точка А лежит между точками В и С, следовательно, отрезок ВС Пересекает прямую B, получаем, что точки В и С лежат в разных полуплоскостях относительно прямой B, и по разные стороны от точки А. Все точки прямой А, лежащие в одной полуплоскости с точкой С, расположены по одну сторону от точки А и образуют одну полупрямую АС, а все точки прямой А, расположенные в одной полуплоскости с точкой В, тоже будут лежать по одну сторону от точки А и образуют полупрямую АВ.

Что и требовалось доказать.

Источник

1. Выбор средств измерений и их применение

Выбор средств измерений при проверке точности деталей — один из важнейших этапов разработки технологических процессов технического контроля.

Основные принципы выбора средств измерений заключаются в следующем: точность средства измерений должна быть достаточно высокой по сравнению с заданной точностью выполнения измеряемого размера, а трудоемкость измерений и их стоимость должны быть возможно более низкими, обеспечивающими наиболее высокие производительность труда и экономичность.

Недостаточная точность измерений приводит к тому, что часть годной продукции бракуют (ошибка первого рода); в то же время по той же причине другую часть фактически негодной продукции принимают как годную (ошибка второго рода).

Излишняя точность измерений, как правило, бывает связана с чрезмерным повышением трудоемкости и стоимости контроля качества продукции, а следовательно, ведет к удорожанию ее производства.

При выборе измерительных средств и методов контроля изделий учитывают

допустимую погрешность измерительного прибора–инструмента;
цену деления шкалы;
порог чувствительности;
пределы измерения, массу, габаритные размеры, рабочую нагрузку и др.

Определяющим фактором является допускаемая погрешность измерительного средства, что вытекает из стандартизованного определения действительного размера как и размера, получаемого в результате измерения с допустимой погрешностью.

Самый простой способ выбора средств измерений основан на том, что точность средства измерений должна быть в несколько раз выше точности изготовления измеряемой детали. При контроле точности технологических процессов измерением точности размеров деталей рекомендуется применять средства измерений с ценой деления не более 1/6 допуска на изготовление.

Значение допустимой погрешности измерения зависит от допуска, который связан с номинальным размером и с квалитетом точности размера контролируемого изделия. Расчетные значения допустимой погрешности измерения в мкм приводятся в стандартных таблицах.

Рекомендуется, чтобы величины допустимых погрешностей измерения для квалитетов 2–9 составляли до 30%, для квалитета 10 и грубее — до 20% допуска на изготовление изделия.

2. Контрольно-измерительные инструменты

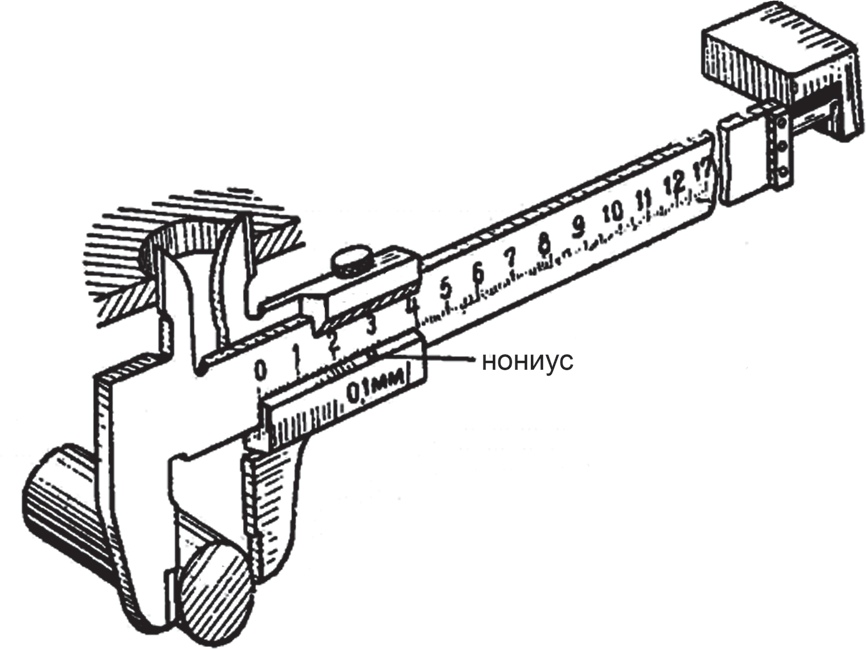
К инструментам с линейным нониусом относятся штангенциркуль, штангенрейсмас и штанген-глубиномер. Основой штангенинструмента является линейка — штанга с нанесенными на ней делениями; это – основная шкала. По штанге движется рамка с вырезом, на наклонной грани которого нанесена нониусная (вспомогательная) шкала.

Штангенциркуль (рис. 2) предназначен для измерения линейных размеров (диаметров, глубины, ширины, толщины и т.п.). На длине 9 мм рамки (нониуса), соответствующей 9 делениям штанги, нанесено 10 равных делений. Таким образом, каждое деление нониуса равно 0,9 мм.

Рис. 2. Методы измерения размеров штангенциркулем

Если поставить рамку так, чтобы шестой штрих нониуса стал против шестого штриха штанги, то зазор между губками будет равен 0,6 мм (рис. 3, А).

Рис. 3. Установка нониуса: А — на размер 0,6 мм; Б — на размер 7 мм; В — на размер 7,4 мм

Если нулевой штрих нониуса совпал с каким-либо штрихом на штанге, например с седьмым, то это деление и указывает действительный размер в миллиметрах, т.е. 7 мм (рис. 3, Б).

Если нулевой штрих нониуса не совпал ни с одним штрихом на штанге, то ближайший штрих на штанге слева от нулевого штриха нониуса показывает целое число миллиметров. Десятые доли миллиметра равны порядковой цифре штриха нониуса вправо, не считая нулевого, который точно совпал со штрихом штанги — основной шкалы (например 7,4 мм на рис. 3, В).

Кроме нониусов с величиной отсчета 0,1 мм применяются нониусы с величиной отсчета 0,05 и 0,02 мм.

Штангенрейсмасы предназначаются для точной разметки и измерения высот от плоских поверхностей.

Штангенрейсмас (рис. 4, а) состоит из основания 8, в котором жестко закреплена штанга 1 со шкалой; рамки 2 с нониусом 6 и стопорным винтом 3; устройства для микрометрической подачи 4, включающего в себя движок, винт, гайку и стопорный винт; сменных ножек для разметки 7 с острием и для измерения высот 9 с двумя измерительными поверхностями, нижней плоской и верхней в виде острого ребра шириной не более 0,2 мм (рис. 4, б); зажима 5 для закрепления ножек 7 и 9 и державки 10 на выступе рамки (рис. 4, в) для игл различной длины.

Рис 4. Штангенрейсмас

Шкала и нониус такие же, как и у других штангенинструментов.

Измерение или разметка штангенрейсмасом производится на разметочной плите. Перед измерением проверяется нулевая установка инструмента. Для этого рамку с ножкой опускают до соприкосновения с плитой или специальной базовой поверхностью (в зависимости от вида ножки). При таком положении нулевое деление нониуса должно совпасть с нулевым делением шкалы штанги.

После выверки штангенрейсмаса можно приступать к измерениям. При измерении высоты детали опускают вручную рамку с ножкой, немного не доводя ее до детали. Дальнейшее перемещение ножки до соприкосновения с деталью осуществляется с помощью гайки микрометрической подачи. Степень прижима ножки к детали определяется на ощупь. В установленном положении рамку закрепляют.

При разметке размер устанавливается по шкалам нониуса и штанги заранее. Риска на детали прочерчивается острым концом ножки при перемещении штангенрейсмаса по плите. При измерении с помощью игл (рис. 4, в) необходимо от показания штангенрейсмаса М вычесть величину m, которая соответствует такому положению рамки 2, когда острие иглы находится в одной плоскости с плоскостью основания .

Индикаторы часового типа. Вследствие небольшого предела измерений инструменты этой группы предназначаются главным образом для относительных (сравнительных) измерений путем определения отклонений от заданного размера. В сочетании со специальными приспособлениями эти приборы могут применяться и для непосредственных измерений. Они используются также и для контроля правильности геометрических форм деталей машин и их взаимного расположения. Наибольшее распространение из приборов этой группы получили индикаторы часового типа (рис. 5, а) с ценой деления 0,01 мм; применяются также индикаторы с ценой деления 0,002 мм.

При перемещении измерительного стержня на 1 мм стрелка индикатора делает полный оборот. Индикаторы, пределы измерения которых более 3 мм, имеют счетчик оборотов стрелки.

Практика измерений. Индикаторы часового типа применяют при измерениях радиального и осевого биения, отклонений от прямолинейности, отклонений положения одной детали относительно другой, при проверке взаимного расположения поверхностей и пр.

Рис. 5. Индикатор часового типа (а) и установка индикатора для измерения: б — на универсальном штативе; в — различные способы крепления индикаторной головки на штативе

При измерениях применяют универсальный штатив и другие приспособления.

Индикатор, установленный в универсальном штативе (рис. 5, б), может занимать самые различные положения по отношению к проверяемому изделию. Конструктивное оформление универсальных штативов может быть различным, но принципиальная схема их остается одной и той же. Варианты приведены на рис. 5, в.

При любом измерении индикатором (абсолютном или относительном) его нужно установить в некоторое начальное положение. Для этого измерительный наконечник приводят в соприкосновение с поверхностью установочной меры (или столика). Индикатор подводят так, чтобы стрелка его сделала 1–2 оборота. Таким образом стержню индикатора дается натяг, чтобы в процессе измерения индикатор мог показать как отрицательные, так и положительные отклонения от начального положения или установочной меры. Стрелка индикатора при этом устанавливается против какого-либо деления шкалы. Дальнейшие отсчеты следует вести от этого показания стрелки, как от начального. Чтобы облегчить отсчеты, начальное показание обычно приводят к нулю. Установка индикатора на нуль осуществляется поворотом циферблата за рифленый ободок.

При измерениях индикаторным нутромером его предварительно настраивают на измеряемый размер по микрометру, блоку плоскопараллельных концевых мер или калиброванному кольцу и после этого устанавливают на нуль.

Настроенный нутромер осторожно вводят в измеряемое отверстие и небольшими покачиваниями (рис. 6, а) определяют отклонение стрелки от нулевого положения. Это и будет отклонение измеряемого размера от того, на который был настроен. В тех случаях, когда измерительный стержень индикаторной головки не может коснуться измеряемой поверхности, прибегают к специальным рычажным приспособлениям, соединенным с корпусом индикатора. Устройство этих приспособлений ясно из рисунка (рис. 6, б).

Рис. 6. Индикаторный нутромер (а) и рычажные приспособления к индикатору (б), применяемые для измерений в труднодоступных местах

Микрометры для наружных измерений (рис. 7), микрометрические нутромеры и микрометрические глубиномеры относятся к микрометрическим инструментам.

Рис. 7. Микрометр для наружных измерений: 1 — пятка; 2 — микрометрический винт; 3 — стопорная гайка; 4 — втулка; 5 — барабан; 6 — трещотка; 7 — скоба

Отсчетное устройство микрометрических инструментов состоит из втулки 1 (рис. 8, а) и барабанчика 2. На втулке по обе стороны продольной линии нанесены две шкалы с делениями через 1 мм так, что верхняя шкала сдвинута по отношению к нижней на 0,5 мм.

На скошенном конце барабанчика имеется круговая шкала с 50 делениями. При вращении барабанчик перемещается вдоль втулки и за один оборот проходит путь, равный 0,5 мм. Следовательно, цена деления шкалы барабанчика равна 0,5:50=0,01 мм.

При измерениях целое число миллиметров отсчитывают по нижней шкале, половины миллиметров — по верхней шкале втулки, а сотые доли миллиметра — по шкале барабанчика. Число сотых долей миллиметра отсчитывают по делению шкалы барабанчика, совпадающему с продольной риской на втулке.

Примеры отсчета по шкалам микрометра приведены на рис. 8.

Рис. 8. Методика отсчета размеров по шкале микрометрического инструмента: а — 11,0 мм; б — 9,36 мм; в — 10,5 мм; г — 9,86 мм

Чтобы при измерении микрометром ограничить силу натяжения на измеряемую деталь и обеспечить постоянство этой силы, микрометр снабжается трещоткой.

Перед тем как прочесть показания микрометра, барабанчик закрепляют с помощью специального стопора.

Кроме обычных штангенциркулей и других инструментов с нониусной шкалой и шкалой часового типа применяют также и модели инструментов с электронными цифровыми индикаторами, которые выводят на экран в цифровом виде показания значений произведенного измерения.

При эксплуатации измерительных приборов следует помнить, что измерительные поверхности у наконечников должны быть чистыми, а измеряемые поверхности деталей должны быть чистыми и их температура не должна отличаться от температуры измерительных приборов. Недопустимо измерять горячие детали точными измерительными приборами. В руках измерительные приборы долго держать нельзя, так как это влияет на точность измерений. Не допускается измерять подвижные детали, потому что это опасно, приводит к быстрому износу измерительных поверхностей инструмента и к потере точности результатов измерения.

При кратковременном и длительном хранении измерительный инструмент протирают мягкой ветошью с авиабензином и смазывают тонким слоем технического вазелина. Измеряющие поверхности наконечников отделяют друг от друга, а стопоры ослабляют. При длительном хранении инструменты обертывают промасленной бумагой.

Перед тем как приступить к измерениям рекомендуют проверить нуль показаний средств измерения. Для этого предварительно настраивают показания шкалы инструмента на измеряемый размер по мерным плиткам (плоскопараллельным концевым мерам) или по калиброванному кольцу или валику и таким образом определяют положение нуля при измерениях.

Щупы служат для определения величины зазоров с точностью 0,01 мм (рис. 9).

Рис. 9. Набор щупов

Щупы изготовляются 1-го и 2-го классов точности с толщиной пластин от 0,03 до 1 мм и с интервалом 0,01 мм или больше, в зависимости от номера набора.

Поверочные плиты (рис. 10) являются основными средствами проверки плоскостности поверхности детали методом на краску. Плиты изготовляют из чугуна размерами от 100х200 до 1000х1500 мм.

На поверхности плит не должно быть коррозийных пятен или раковин.

Поверочные плиты служат не только для контроля плоскостности. Их широко используют в качестве базы для различных контрольных операций с применением универсальных средств измерений (рейсмусов, индикаторных стоек и др.)

Рис. 10. Поверочные плиты

Поверочные линейки стальные. Отклонения от плоскостности и прямолинейности (отклонения формы плоских поверхностей) контролируют с помощью поверочных линеек (рис. 11). Поверочные линейки выпускают лекальные с двусторонним скосом (рис. 11, а); трехгранные (рис. 11, б) и четырехгранные (рис. 11, в); с широкой рабочей поверхностью (прямоугольного сечения (рис. 11, г) и двутаврового сечения (рис. 11, д), «чугунные мостики» (рис. 11, е).

Рис. 11. Поверочные линейки

Линейки выпускаются различных размеров (LxHxB мм): а – до 320х40х8; б – до 320х30; в – до 320х25; г – до 1000х60х12; д – до 4000х160х30.

Поверочные линейки изготовляют длиной: лекальные — до 500 мм, «чугунные мостики» — до 2500 мм и более. Лекальные применяют для контроля прямолинейности поверхности детали «на просвет», а поверочные линейки «чугунные мостики» — применяют для проверки прямолинейности «на краску», с помощью щупа или папиросной бумажки.

При проверке на просвет (рис. 12, а) лекальную линейку укладывают острым скосом на проверяемую поверхность, а источник света помещают сзади линейки и детали. Минимальная ширина щели, улавливаемая глазом, составляет 3…5 мкм. Для контроля щели просвета обычно используют щупы.

Рис. 12. Схема контроля отклонения от плоскостности лекальной линейкой «на просвет»: а — визуально; б — с образцом просветов

Измерение отклонений от прямолинейности лекальными линейками «на просвет» требует навыка от исполнителя. Для выработки навыка оценивать на глаз по величине просвета величину отклонения от прямолинейности применяют образец просветов (рис. 12, б), который состоит из лекальной линейки 1, комплекта из четырех концевых мер длины с градацией 1 мкм, двух одинаковых концевых мер длины (2) и стеклянной пластины 3. При измерении между концевыми мерами длины и ребром линейки образуются «просветы», окрашенные в разные цвета вследствие дифракции видимого света и от величины зазора между линейкой и концевой мерой длины.

Источник