Какую зависимость сопротивления проводника от его размеров и свойства
Сопротивление различных проводников зависит от материала, из которого они изготовлены.
Можно проверить это практически на следующем опыте.
Рисунок 1. Опыт, показывающий зависимость электрического сопротивления от материала проводника
Подберем два или три проводника из различных материалов, возможно меньшего, но одинакового поперечного сечения, например, один медный, другой стальной, третий никелиновый. Укрепим на планке два зажима а и б на расстоянии 1 —1,5 м один от другого (рис. 1) и подключим к ним аккумулятор через амперметр. Теперь поочередно между зажимами а и б будем на 1—2 сек включать сначала медный, потом стальной и, наконец, никелиновый проводник, наблюдая в каждом случае за отклонением стрелки амперметра. Нетрудно будет заметить, что наибольший по величине ток пройдет по медному проводнику, а наименьший — по никелиновому.
Из этого следует, что сопротивление медного проводника меньше, чем стального, а сопротивление стального проводника меньше, чем никелинового.
Таким образом, электрическое сопротивление проводника зависит от материала, из которою он изготовлен.
Для характеристики электрического сопротивления различных материалов введено понятие о так называемом удельном сопротивлении.
Определение: Удельным сопротивлением называется сопротивление проводника длиной в 1 м и сечением в 1 мм2 при температуре +20 С°.
Удельное сопротивление обозначается буквой ρ («ро») греческого алфавита.
Каждый материал, из которого изготовляется проводник, обладает определенным удельным сопротивлением. Например, удельное сопротивление меди равно 0,0175 Ом*мм2/м, т. е. медный проводник длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,0175 Ом.
Ниже приводится таблица удельных сопротивлений материалов, наиболее часто применяемых в электротехнике.
Удельные сопротивления материалов, наиболее часто применяемых в электротехнике
| Материал | Удельное сопротивление, Ом*мм2/м |
| Серебро | 0,016 |
| Медь | 0,0175 |
| Алюминий | 0,0295 |
| Железо | 0,09-0,11 |
| Сталь | 0,125-0,146 |
| Свинец | 0,218-0,222 |
| Константан | 0,4-0,51 |
| Манганин | 0,4-0,52 |
| Никелин | 0,43 |
| Вольфрам | 0,503 |
| Нихром | 1,02-1,12 |
| Фехраль | 1,2 |
| Уголь | 10-60 |
Любопытно отметить, что например, нихромовый провод длиною 1 м обладает примерно таким же сопротивлением, как медный провод длиною около 63 м (при одинаковом сечении).
Разберем теперь, как влияют размеры проводника, т. е. длина и поперечное сечение, на величину его сопротивления.
Воспользуемся для этого схемой, изображенной на рис. 1. Включим между зажимами а и б для большей наглядности опыта проволоку из никелина. Заметив показание амперметра, отключим от зажима б проводник, которой соединяет прибор с минусом аккумулятора, и освободившимся концом проводника прикоснемся к никелиновой проволоке на некотором удалении от зажима а (рис. 2). Уменьшив таким образом длину проводника, включенного в цепь, нетрудно заметить по показанию амперметра, что ток в цепи увеличился.
Рисунок 2. Опыт, показывающий зависимость электрического сопротивления от длины проводника
Это говорит о том, что с уменьшением длины проводника сопротивление его уменьшается. Если же перемещать конец проводника по никелиновой проволоке вправо, т. е. к зажиму б, то, наблюдая за показаниями амперметра, можно сделать вывод, что с увеличением длины проводника сопротивление его увеличивается.
Таким образом, сопротивление проводника прямо пропорционально его длине, т. е. чем длиннее проводник, тем больше его электрическое сопротивление..
Выясним теперь, как зависит сопротивление проводника от его поперечного сечения, т. е. от толщины.
Подберем для этого два или три проводника из одного и того же материала (медь, железо или никелин), но различного поперечного сечения и включим их поочередно между зажимами а и б, как указано на рис. 1.
Наблюдая каждый раз за показаниями амперметра, можно убедиться, что чем тоньше проводник, тем меньше ток в цепи, а следовательно, тем больше сопротивление проводника. И, наоборот, чем толще проводник, тем больше ток в цепи, а следовательно, тем меньше сопротивление проводника.
Значит, сопротивление проводника обратно пропорционально площади его поперечного сечения, т. е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.
Чтобы лучше уяснить эту зависимость, представьте себе две пары сообщающихся сосудов (рис. 3), причем у одной пары сосудов соединяющая трубка тонкая, а у другой — толстая.
Рисунок 3. Вода по толстой трубке перейдет быстрее, чем по тонкой
Ясно, что при заполнении водой одного из сосудов (каждой пары) переход ее в другой сосуд по толстой трубке произойдет гораздо быстрее, чем по тонкой. Это значит, что толстая трубка окажет меньшее сопротивление течению воды. Точно так же и электрическому току легче пройти по толстому проводнику, чем по тонкому, т. е. первый оказывает ему меньшее сопротивление, чем второй.
Обобщая результаты произведенных нами опытов, можно сделать следующий общий вывод:
электрическое сопротивление проводника равно удельному сопротивлению материала, из которого этот проводник сделан, умноженному на длину проводника и деленному на площадь его поперечного сечения..
Математически эта зависимость выражается следующей формулой:
где R—сопротивление проводника в Ом;
ρ — удельное сопротивление материала в Ом*мм2/м;
l — длина проводника в м;
S—площадь поперечного сечения проводника в мм2.
Примечание. Площадь поперечного сечения круглого проводника вычисляется по формуле
где π—постоянная величина, равная 3,14;
d—диаметр проводника.
Указанная выше зависимость дает возможность определить длину проводника или его сечение, если известны одна из этих величин и сопротивление проводника.
Так, например, длина проводника определяется по формуле:
Если же необходимо определить площадь поперечного сечения проводника, то формула принимает следующий вид:
Решив это равенство относительно ρ, получим выражение для определения удельного сопротивления проводника:
Последней формулой приходится пользоваться в тех случаях, когда известны сопротивление и размеры проводника, а его материал неизвестен и к тому же трудно определим по внешнему виду. Определив по формуле удельное сопротивление проводника, можно найти материал, обладающий таким удельным сопротивлением.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Источник
Любое тело, по которому протекает электрический ток, оказывает ему определенное сопротивление. Свойство материала проводника препятствовать прохождению через него электрического тока называется электрическим сопротивлением.
Сопротивление обозначается латинскими буквами R или r.
За единицу электрического сопротивления принят Ом.
Сопротивление различных проводников зависит от материала, из которого они изготовлены. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.
Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм2. Удельное сопротивление обозначается буквой греческого алфавита ρ. Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.
Сопротивление проводника прямо пропорционально его длине, т. е. чем длиннее проводник, тем больше его электрическое сопротивление.
Сопротивление проводника обратно пропорционально площади его поперечного сечения, т. е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.
Электрическое сопротивление проводника равно удельному сопротивлению материала, из которого этот проводник сделан, умноженному на длину проводника и деленному на площадь площадь поперечного сечения проводника:
R = р l / S,
где – R – сопротивление проводника, ом, l – длина в проводника в м, S – площадь поперечного сечения проводника, мм2.
Еще одной причиной, влияющей на сопротивление проводников, являетсятемпература.
Установлено, что с повышением температуры сопротивление металлических проводников возрастает, а с понижением уменьшается. С понижением же температуры создаются лучшие условия для направленного движения электронов, и сопротивление проводника уменьшается. Этим объясняется интересное явление — сверхпроводимость металлов.
ЭДС источника тока. Закон Ома для полной цепи с ЭДС.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника(ЭДС):
Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Сопротивление r неоднородного участка можно рассматривать как внутреннее сопротивление источника тока.
63. Соединение проводников.
Проводники в электрических цепях могут соединяться последовательно и параллельно.
При последовательном соединении проводников сила тока во всех проводниках одинакова:
По закону Ома, напряжения U1 и U2 на проводниках равны
Общее напряжение U на обоих проводниках равно сумме напряжений U1 и U2:
U = U1 + U2 = I(R1 + R2) = IR,
где R – электрическое сопротивление всей цепи. Отсюда следует:
Источник
Ïîíÿòèå îá ýëåêòðè÷åñêîì ñîïðîòèâëåíèè è ïðîâîäèìîñòè
Ëþáîå òåëî, ïî êîòîðîìó ïðîòåêàåò ýëåêòðè÷åñêèé òîê, îêàçûâàåò åìó îïðåäåëåííîå ñîïðîòèâëåíèå. Ñâîéñòâî ìàòåðèàëà ïðîâîäíèêà ïðåïÿòñòâîâàòü ïðîõîæäåíèþ ÷åðåç íåãî ýëåêòðè÷åñêîãî òîêà íàçûâàåòñÿ ýëåêòðè÷åñêèì ñîïðîòèâëåíèåì.
Ýëåêòðîííàÿ òåîðèÿ òàê îáúÿñíÿåò ñóùíîñòü ýëåêòðè÷åñêîãî ñîïðîòèâëåíèÿ ìåòàëëè÷åñêèõ ïðîâîäíèêîâ. Ñâîáîäíûå ýëåêòðîíû ïðè äâèæåíèè ïî ïðîâîäíèêó áåñ÷èñëåííîå êîëè÷åñòâî ðàç âñòðå÷àþò íà ñâîåì ïóòè àòîìû è äðóãèå ýëåêòðîíû è, âçàèìîäåéñòâóÿ ñ íèìè, íåèçáåæíî òåðÿþò ÷àñòü ñâîåé ýíåðãèè. Ýëåêòðîíû èñïûòûâàþò êàê áû ñîïðîòèâëåíèå ñâîåìó äâèæåíèþ. Ðàçëè÷íûå ìåòàëëè÷åñêèå ïðîâîäíèêè, èìåþùèå ðàçëè÷íîå àòîìíîå ñòðîåíèå, îêàçûâàþò ðàçëè÷íîå ñîïðîòèâëåíèå ýëåêòðè÷åñêîìó òîêó.
Òî÷íî òåì æå îáúÿñíÿåòñÿ ñîïðîòèâëåíèå æèäêèõ ïðîâîäíèêîâ è ãàçîâ ïðîõîæäåíèþ ýëåêòðè÷åñêîãî òîêà. Îäíàêî íå ñëåäóåò çàáûâàòü, ÷òî â ýòèõ âåùåñòâàõ íå ýëåêòðîíû, à çàðÿæåííûå ÷àñòèöû ìîëåêóë âñòðå÷àþò ñîïðîòèâëåíèå ïðè ñâîåì äâèæåíèè.
Ñîïðîòèâëåíèå îáîçíà÷àåòñÿ ëàòèíñêèìè áóêâàìè R èëè r.
Çà åäèíèöó ýëåêòðè÷åñêîãî ñîïðîòèâëåíèÿ ïðèíÿò îì.
Îì åñòü ñîïðîòèâëåíèå ñòîëáà ðòóòè âûñîòîé 106,3 ñì ñ ïîïåðå÷íûì ñå÷åíèåì 1 ìì2 ïðè òåìïåðàòóðå 0° Ñ.
Åñëè, íàïðèìåð, ýëåêòðè÷åñêîå ñîïðîòèâëåíèå ïðîâîäíèêà ñîñòàâëÿåò 4 îì, òî çàïèñûâàåòñÿ ýòî òàê: R = 4 îì èëè r = 4îì.
Äëÿ èçìåðåíèÿ ñîïðîòèâëåíèé áîëüøîé âåëè÷èíû ïðèíÿòà åäèíèöà, íàçûâàåìàÿ ìåãîìîì.
Îäèí ìåãîì ðàâåí îäíîìó ìèëëèîíó îì.
×åì áîëüøå ñîïðîòèâëåíèå ïðîâîäíèêà, òåì õóæå îí ïðîâîäèò ýëåêòðè÷åñêèé òîê, è, íàîáîðîò, ÷åì ìåíüøå ñîïðîòèâëåíèå ïðîâîäíèêà, òåì ëåã÷å ýëåêòðè÷åñêîìó òîêó ïðîéòè ÷åðåç ýòîò ïðîâîäíèê.
Ñëåäîâàòåëüíî, äëÿ õàðàêòåðèñòèêè ïðîâîäíèêà (ñ òî÷êè çðåíèÿ ïðîõîæäåíèÿ ÷åðåç íåãî ýëåêòðè÷åñêîãî òîêà) ìîæíî ðàññìàòðèâàòü íå òîëüêî åãî ñîïðîòèâëåíèå, íî è âåëè÷èíó, îáðàòíóþ ñîïðîòèâëåíèþ è íàçûâàåìóþ, ïðîâîäèìîñòüþ.
Ýëåêòðè÷åñêîé ïðîâîäèìîñòüþ íàçûâàåòñÿ ñïîñîáíîñòü ìàòåðèàëà ïðîïóñêàòü ÷åðåç ñåáÿ ýëåêòðè÷åñêèé òîê.
Òàê êàê ïðîâîäèìîñòü åñòü âåëè÷èíà, îáðàòíàÿ ñîïðîòèâëåíèþ, òî è âûðàæàåòñÿ îíà êàê 1/R,îáîçíà÷àåòñÿ ïðîâîäèìîñòü ëàòèíñêîé áóêâîé g.
Âëèÿíèå ìàòåðèàëà ïðîâîäíèêà, åãî ðàçìåðîâ è îêðóæàþùåé òåìïåðàòóðû íà âåëè÷èíó ýëåêòðè÷åñêîãî ñîïðîòèâëåíèÿ
Ñîïðîòèâëåíèå ðàçëè÷íûõ ïðîâîäíèêîâ çàâèñèò îò ìàòåðèàëà, èç êîòîðîãî îíè èçãîòîâëåíû. Äëÿ õàðàêòåðèñòèêè ýëåêòðè÷åñêîãî ñîïðîòèâëåíèÿ ðàçëè÷íûõ ìàòåðèàëîâ ââåäåíî ïîíÿòèå òàê íàçûâàåìîãî óäåëüíîãî ñîïðîòèâëåíèÿ.
Óäåëüíûì ñîïðîòèâëåíèåì íàçûâàåòñÿ ñîïðîòèâëåíèå ïðîâîäíèêà äëèíîé 1 ì è ïëîùàäüþ ïîïåðå÷íîãî ñå÷åíèÿ 1 ìì2. Óäåëüíîå ñîïðîòèâëåíèå îáîçíà÷àåòñÿ áóêâîé ãðå÷åñêîãî àëôàâèòà ð. Êàæäûé ìàòåðèàë, èç êîòîðîãî èçãîòîâëÿåòñÿ ïðîâîäíèê, îáëàäàåò ñâîèì óäåëüíûì ñîïðîòèâëåíèåì.
Íàïðèìåð, óäåëüíîå ñîïðîòèâëåíèå ìåäè ðàâíî 0,017, ò. å. ìåäíûé ïðîâîäíèê äëèíîé 1 ì è ñå÷åíèåì 1 ìì2 îáëàäàåò ñîïðîòèâëåíèåì 0,017 îì. Óäåëüíîå ñîïðîòèâëåíèå àëþìèíèÿ ðàâíî 0,03, óäåëüíîå ñîïðîòèâëåíèå æåëåçà – 0,12, óäåëüíîå ñîïðîòèâëåíèå êîíñòàíòàíà – 0,48, óäåëüíîå ñîïðîòèâëåíèå íèõðîìà – 1-1,1.
Ïîäðîáíåå îá ýòîì ÷èòàéòå çäåñü: ×òî òàêîå óäåëüíîå ýëåêòðè÷åñêîå ñîïðîòèâëåíèå
Ñîïðîòèâëåíèå ïðîâîäíèêà ïðÿìî ïðîïîðöèîíàëüíî åãî äëèíå, ò. å. ÷åì äëèííåå ïðîâîäíèê, òåì áîëüøå åãî ýëåêòðè÷åñêîå ñîïðîòèâëåíèå.
Ñîïðîòèâëåíèå ïðîâîäíèêà îáðàòíî ïðîïîðöèîíàëüíî ïëîùàäè åãî ïîïåðå÷íîãî ñå÷åíèÿ, ò. å. ÷åì òîëùå ïðîâîäíèê, òåì åãî ñîïðîòèâëåíèå ìåíüøå, è, íàîáîðîò, ÷åì òîíüøå ïðîâîäíèê, òåì åãî ñîïðîòèâëåíèå áîëüøå.
×òîáû ëó÷øå ïîíÿòü ýòó çàâèñèìîñòü, ïðåäñòàâüòå ñåáå äâå ïàðû ñîîáùàþùèõñÿ ñîñóäîâ, ïðè÷åì ó îäíîé ïàðû ñîñóäîâ ñîåäèíÿþùàÿ òðóáêà òîíêàÿ, à ó äðóãîé òîëñòàÿ. ßñíî, ÷òî ïðè çàïîëíåíèè âîäîé îäíîãî èç ñîñóäîâ (êàæäîé ïàðû) ïåðåõîä åå â äðóãîé ñîñóä ïî òîëñòîé òðóáêå ïðîèçîéäåò ãîðàçäî áûñòðåå, ÷åì ïî òîíêîé, ò. å. òîëñòàÿ òðóáêà îêàæåò ìåíüøåå ñîïðîòèâëåíèå òå÷åíèþ âîäû. Òî÷íî òàê æå è ýëåêòðè÷åñêîìó òîêó ëåã÷å ïðîéòè ïî òîëñòîìó ïðîâîäíèêó, ÷åì ïî òîíêîìó, ò. å. ïåðâûé îêàçûâàåò åìó ìåíüøåå ñîïðîòèâëåíèå, ÷åì âòîðîé.
Ýëåêòðè÷åñêîå ñîïðîòèâëåíèå ïðîâîäíèêà ðàâíî óäåëüíîìó ñîïðîòèâëåíèþ ìàòåðèàëà, èç êîòîðîãî ýòîò ïðîâîäíèê ñäåëàí, óìíîæåííîìó íà äëèíó ïðîâîäíèêà è äåëåííîìó íà ïëîùàäü ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ ïðîâîäíèêà:
R = p l / S,
ãäå – R – ñîïðîòèâëåíèå ïðîâîäíèêà, îì, l – äëèíà â ïðîâîäíèêà â ì, S – ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ ïðîâîäíèêà, ìì2.
Ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ êðóãëîãî ïðîâîäíèêà âû÷èñëÿåòñÿ ïî ôîðìóëå:
S = Ïè õ d2 / 4
ãäå Ïè – ïîñòîÿííàÿ âåëè÷èíà, ðàâíàÿ 3,14; d – äèàìåòð ïðîâîäíèêà.
À òàê îïðåäåëÿåòñÿ äëèíà ïðîâîäíèêà:
l = S R / p,
Ýòà ôîðìóëà äàåò âîçìîæíîñòü îïðåäåëèòü äëèíó ïðîâîäíèêà, åãî ñå÷åíèå è óäåëüíîå ñîïðîòèâëåíèå, åñëè èçâåñòíû îñòàëüíûå âåëè÷èíû, âõîäÿùèå â ôîðìóëó.
Åñëè æå íåîáõîäèìî îïðåäåëèòü ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ ïðîâîäíèêà, òî ôîðìóëó ïðèâîäÿò ê ñëåäóþùåìó âèäó:
S = p l / R
Ïðåîáðàçóÿ òó æå ôîðìóëó è ðåøèâ ðàâåíñòâî îòíîñèòåëüíî ð, íàéäåì óäåëüíîå ñîïðîòèâëåíèå ïðîâîäíèêà:
ð = R S / l
Ïîñëåäíåé ôîðìóëîé ïðèõîäèòñÿ ïîëüçîâàòüñÿ â òåõ ñëó÷àÿõ, êîãäà èçâåñòíû ñîïðîòèâëåíèå è ðàçìåðû ïðîâîäíèêà, à åãî ìàòåðèàë íåèçâåñòåí è ê òîìó æå òðóäíî îïðåäåëèì ïî âíåøíåìó âèäó. Äëÿ ýòîãî íàäî îïðåäåëèòü óäåëüíîå ñîïðîòèâëåíèå ïðîâîäíèêà è, ïîëüçóÿñü òàáëèöåé, íàéòè ìàòåðèàë, îáëàäàþùèé òàêèì óäåëüíûì ñîïðîòèâëåíèåì.
Åùå îäíîé ïðè÷èíîé, âëèÿþùåé íà ñîïðîòèâëåíèå ïðîâîäíèêîâ, ÿâëÿåòñÿ òåìïåðàòóðà.
Óñòàíîâëåíî, ÷òî ñ ïîâûøåíèåì òåìïåðàòóðû ñîïðîòèâëåíèå ìåòàëëè÷åñêèõ ïðîâîäíèêîâ âîçðàñòàåò, à ñ ïîíèæåíèåì óìåíüøàåòñÿ. Ýòî óâåëè÷åíèå èëè óìåíüøåíèå ñîïðîòèâëåíèÿ äëÿ ïðîâîäíèêîâ èç ÷èñòûõ ìåòàëëîâ ïî÷òè îäèíàêîâî è â ñðåäíåì ðàâíî 0,4% íà 1°C. Ñîïðîòèâëåíèå æèäêèõ ïðîâîäíèêîâ è óãëÿ ñ óâåëè÷åíèåì òåìïåðàòóðû óìåíüøàåòñÿ.
Ýëåêòðîííàÿ òåîðèÿ ñòðîåíèÿ âåùåñòâà äàåò ñëåäóþùåå îáúÿñíåíèå óâåëè÷åíèþ ñîïðîòèâëåíèÿ ìåòàëëè÷åñêèõ ïðîâîäíèêîâ ñ ïîâûøåíèåì òåìïåðàòóðû. Ïðè íàãðåâàíèè ïðîâîäíèê ïîëó÷àåò òåïëîâóþ ýíåðãèþ, êîòîðàÿ íåèçáåæíî ïåðåäàåòñÿ âñåì àòîìàì âåùåñòâà, â ðåçóëüòàòå ÷åãî âîçðàñòàåò èíòåíñèâíîñòü èõ äâèæåíèÿ. Âîçðîñøåå äâèæåíèå àòîìîâ ñîçäàåò áîëüøåå ñîïðîòèâëåíèå íàïðàâëåííîìó äâèæåíèþ ñâîáîäíûõ ýëåêòðîíîâ, îò÷åãî è âîçðàñòàåò ñîïðîòèâëåíèå ïðîâîäíèêà. Ñ ïîíèæåíèåì æå òåìïåðàòóðû ñîçäàþòñÿ ëó÷øèå óñëîâèÿ äëÿ íàïðàâëåííîãî äâèæåíèÿ ýëåêòðîíîâ, è ñîïðîòèâëåíèå ïðîâîäíèêà óìåíüøàåòñÿ. Ýòèì îáúÿñíÿåòñÿ èíòåðåñíîå ÿâëåíèå ñâåðõïðîâîäèìîñòü ìåòàëëîâ.
Ñâåðõïðîâîäèìîñòü, ò. å. óìåíüøåíèå ñîïðîòèâëåíèÿ ìåòàëëîâ äî íóëÿ, íàñòóïàåò ïðè îãðîìíîé îòðèöàòåëüíîé òåìïåðàòóðå -273° C, íàçûâàåìîé àáñîëþòíûì íóëåì. Ïðè òåìïåðàòóðå àáñîëþòíîãî íóëÿ àòîìû ìåòàëëà êàê áû çàñòûâàþò íà ìåñòå, ñîâåðøåííî íå ïðåïÿòñòâóÿ äâèæåíèþ ýëåêòðîíîâ.
Источник
Подключив источник тока к проводящей цепи, с применением мультиметра измеряют разницу потенциалов (напряжение) в контрольных точках. Опытным путем несложно установить, что электрические параметры меняются при использовании резистора, изготовленного из разных материалов. Аналогичные результаты получают, экспериментируя с различными поперечными сечениями. С помощью этой статьи можно узнать, от чего зависит сопротивление проводника. Полученные знания пригодятся для создания функциональных электрических схем. Они нужны для корректного ремонта и модернизации радиотехнических устройств, обеспечения личной безопасности в ходе выполнения отдельных рабочих операций.
В ходе эксперимента несложно установить зависимость измеряемых величин от параметров проводника
Понятие электрического сопротивления проводника
Классическое определение объясняет электрический ток движением «свободных» (валентных) электронов. Его обеспечивает созданное источником электрическое поле. Перемещение в металле затрудняют не только нормальные компоненты кристаллической решетки, но и дефектные участки, примеси, неоднородные области. В ходе столкновений с препятствиями за счет перехода импульса в тепловую энергию происходит повышение температуры.
Наглядный пример – нагрев воды кипятильником
В газах, электролитах и других материалах несколько отличная физика явления. Линейные зависимости наблюдаются в металлах и других проводниках. Базовые соотношения выражены известной формулой закона Ома:
R (электрическое сопротивление) = U (напряжение)/ I (сила тока).
Для удобства часто используют обратную величину, проводимость (G = 1/R). Она обозначает способность определенного материала пропускать ток с определенными потерями.
Для упрощения иногда применяют пример с водопроводом. Движущаяся жидкость – аналог тока. Давление – эквивалент напряжения. Уменьшением (увеличением) поперечного сечения или положением запорного устройства определяют условия перемещения. Подобным образом изменяют основные параметры электрических цепей с помощью сопротивления (R).
К сведению. Количество жидкости, проходящее за единицу времени через контрольное сечение трубы, – эквивалент электрической мощности.
Зависимость от свойств материала
Для стандартизации приняли единицу измерения 1 Ом. Это сопротивление создает столбик из ртути толщиной 1 кв. мм, высотой – 1063 мм. Измерения выполняются при поддержании нулевой температуры.
Чтобы упростить расчеты, применяют удельное значение сопротивления Rуд, которое создают проводники из других материалов (Длина Х Площадь сечения = 1 000 мм х 1 кв. мм).
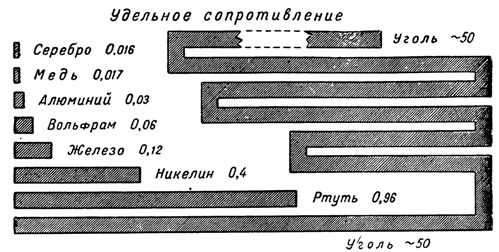
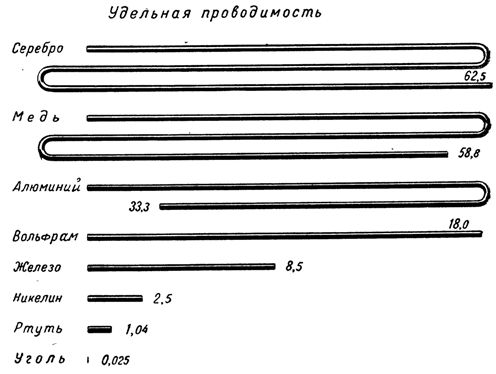
Удельное сопротивление (проводимость)
На рисунке обозначено Rуд (серебра) = 0,016. Это значит, что метровый проводник с нормированной площадью сечения 1 мм кв. создает электрическое сопротивление 0,016 Ом. Сведения о других материалах можно взять из справочника.
Зависимость от свойств напряжения
После простого преобразования основной формулы можно составить корректное выражения для напряжения:
U = I * R.
Источник тока генерирует электричество. Подключенный резистор потребляет энергию с трансформацией в тепло. Для подержания определенной силы тока необходимо установить соответствующее напряжение.
Измерительная схема, графики
На графиках показаны вольтамперные характеристики разных приборов. Первые два демонстрируют линейные зависимости, в которых изменяется только угол наклона прямой линии (зависимость от электрического сопротивления резистора).
Если подключить полупроводниковый диод, график существенно изменится. По рисунку можно определить малое сопротивление в области положительных значений U. Однако после изменения полярности увеличение отрицательного напряжения не сопровождается аналогичным изменением силы тока. Одностороннюю проводимость, в частности, используют для выпрямления сигналов.
На последнем графике сдвинутая точка перехода нулевого значения силы тока обозначает ЭДС источника питания. Как и в предыдущем примере, небольшой угол по отношению к вертикали показывает малое внутреннее сопротивление АКБ.
Зависимость от геометрии
Из раздела с описанием удельных параметров понятно, что электрическое сопротивление проводника зависит от длины. Если взять образец из серебра (площадь нормированного сечения 1 кв. мм) при длине 6,8 м, несложно вычислить значение R = 6,8 * 0,016 = 0,1088 Ом.
Аналогичным образом решают иные практические задачи. Чтобы создать провод с электросопротивлением 100 Ом понадобится серебряная жила длиной 6 250 м = 100/ 0,016. Если применить металлический проводник из железа, длина составит 833 м = 100/0,12.
Следующий решающий фактор – площадь поперечного сечения. Для наглядности можно использовать пример с перекачиванием жидкости из основного бака в две разные емкости. Создать необходимый напор несложно поднятием главного резервуара на небольшую высоту. Применив трубки с разным диаметром протоков, можно увидеть разницу в скорости заполнения контрольных объемов. Если показания будут измеряться при желании несложно составить пропорциональные зависимости с учетом исходных геометрических параметров транспортных каналов.
Размерность проводников также имеет значение. Электрическое сопротивление (R) равно удельному значению для определенного материала (Rуд), умноженному на длину (L) и деленому на соответствующее поперечное сечение (S). Если известен только диаметр, то для круглой жилы можно применить классическую формулу из школьного курса геометрии:
S = (π * d2)/4 = (3,14 * d2)/4.
Длину вычисляют по преобразованному выражению:
L = S * (R/ Rуд).
Эти пропорции демонстрируют, от чего зависит сопротивление.
Расчёт сопротивления проводника
Выше были рассмотрены упрощенные методики, которые надо корректировать с учетом реальных условий. Так, существенное влияние на проводимость материалов оказывает температура. В серийных проводниках (медь, алюминий) значение данного параметра увеличивается в пропорции 0,3-0,5% на каждый градус. В составах на основе угля и электролитах наблюдается обратный эффект – уменьшение сопротивления.
Без удерживающих струн и других приспособлений для фокусов обеспечивается настоящая левитация с применением сверхпроводимости
Показанный на рисунке эксперимент можно воспроизвести, понизив температуру металла до «абсолютного нуля» (-273°C). При таком экстремальном охлаждении атомарная решетка фиксируется в стабильном положении.
Это состояние создает идеальные условия для перемещения электронов. Отсутствие препятствий сопровождается минимальными потерями, что объясняет перспективность направления для создания эффективных линий передачи энергии. Пример на рисунке демонстрирует улучшенные эксплуатационные параметры транспортных коммуникаций. В данном случае можно исключить силы трения.
Комбинация трубы с безвоздушным пространством и сверхпроводимости улучшает характеристики перспективных транспортных систем
Понятно, что для улучшения экономических показателей необходимо повысить рабочую температуру при сохранении хорошей проводимости. Однако новейшие научные достижения в соответствующей области позволяют рассчитывать на положительный результат в близком будущем.
Следует подчеркнуть! На практике могут понадобится разные технологии вычислений. Например, материал неизвестен. Сложно идентифицировать его по внешним признакам. Для качественного химического лабораторного анализа, кроме соответствующих навыков, необходимо специальное оснащение.
Однако при необходимости нетрудно вывести удельный показатель:
Rуд = R * S /L.
Геометрические параметры измеряют стандартными инструментами (линейкой, штангенциркулем). По типовой схеме измерений с помощью мультиметра уточняют электрическое сопротивление. Для вычисления Rуд пользуются представленной выше формулой. В справочнике выбирают позицию, соответствующую результату расчета. По такой же методике можно определить иные неизвестные значения, например, длину кабеля в подземной трассе.
В реальных расчетах для повышения точности учитывают реактивные компоненты проводников. Например, индуктивность длинной прямой линии определяют по формуле:
И = (m0/2π) * L *(mc * ln(L/r) +1/4m,
где:
- m – магнитная проницаемость материала (о – постоянная, с – окружающей среды);
- r и L – радиус и длина проводника, соответственно.
При повышении частоты приходится учитывать растекание тока в поверхностной зоне и вихревые изменения.
Представленные теоретические знания пригодятся для расчета и создания реостата – прибора с регулируемым сопротивлением. Они нужны для предотвращения электротравм с применением точного расчета защитных цепей и специализированных автоматов (предохранителей).
Видео
Источник