Каком объеме раствора содержится

Задача 416.
В каком объеме 0,1н. раствора содержится 8г CuSO4?
Решение:
Эквивалентная масса соли равна молекулярной массе данной соли делённой на общую валентность металла, входящего в состав соли:

где
MЭ(В) – молярная масса эквивалента соли, г/моль; М(В) – молярная масса соли; n – коэффициент при атоме металла; A – валентность металла.
Отсюда

Массу 0,1 эквивалента соли CuSO4 находим из пропорции:

8г CuSO4 соответствует 0,1 эквиваленту, значит, эта масс содержится в 1л раствора.
Ответ: 1л.
Задача 417.
Для нейтрализации 30мл 0,1н. раствора щелочи потребовалось 12мл раствора кислоты. Определить нормальность кислоты.
Решение:
Для определения нормальности кислоты используем математическое выражение следствия из закона эквивалентности (так называемое правило пропорциональности):
CЭ(А) .V(A) = CЭ(B) . V(B),
CЭ(А) и CЭ(B) – нормальные концентрации эквивалентов веществ А и В, моль/л; V(A) и V(B) – объёмы растворов веществ А и В.
По условию задачи известны CЭ(щелочи), V(щелочи) и V(кислоты), то нетрудно вычислить СЭ(кислоты) по формуле:

Ответ: 0,25н.
Задача 418.
Найти молярность 36,2%-ного (по массе) раствора НСI, плотность которого 1,18г/мл.
Решение:
Молярная(объёмно-молярная) концентрация показывает число молей растворённого вещества, содержащихся в 1 литре раствора. Масса 1 литра раствора HCl (р = 1,18г/мл) равна 1180г (1000 . 1,18 = 1180).
Массу HCl, содержащуюся в 1 литре раствора рассчитаем по формуле:

где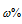 – массовая доля растворённого вещества; m(в-ва) – масса растворённого вещества; m(р-ра) – масса раствора.
– массовая доля растворённого вещества; m(в-ва) – масса растворённого вещества; m(р-ра) – масса раствора.
Тогда

Молярную концентрацию раствора (СМ) получим делением числа граммов HCl в 1л раствора на молярную массу HCl (36,5г/моль):

Ответ: 11,7 моль/л.
Задача 419.
В каком объеме 1М раствора и в каком объеме 1н. раствора содержится 114г Al2(SО4)3?
Решение:
Молярная(объёмно-молярная) концентрация показывает число молей растворённого вещества, содержащихся в 1 литре раствора. Молярная концентрация эквивалента (или нормальность) показывает число эквивалентов растворённого вещества, содержащихся в 1 литре раствора.
M[Al2(SО4)3] = 342 г/моль. Эквивалентная масса соли равна молекулярной массе данной соли делённой на общую валентность металла, входящего в состав соли:

где
MЭ(В) – молярная масса эквивалента соли, г/моль; М(В) – молярная масса соли; n – коэффициент при атоме металла; A – валентность металла.
Отсюда

Находим, в каком объёме 1М раствора содержится 114г Al2(SО4)3 из пропорции:

Теперь находим объём 1н раствора, в котором содержится 114г Al2(SО4)3, составив про-порцию:

Ответ: 0,333л; 2л.
Задача 420.
Растворимость хлорида кадмия при 20°С равна 114,1г в 100г воды. Вычислить массовую долю и моляльность CdCl2 в насыщенном растворе.
Решение:
M(CdCl2) = 183,324г/моль.
Растворимость вещества измеряется содержанием вещества в его насыщенном растворе. Обычно растворимость твёрдых веществ и жидкостей выражают значением коэффициента растворимости, т.е. массой вещества, растворяющегося при данных условиях в 100 г воды или другого растворителя с образованием насыщенного раствора.
m(CdCl2) = 114,1г. m(р-ра) = m(CdCl2) + m(H2O) = 114,1 + 100 = 241,1г.
Массовую долю CdCl2 вычислим по формуле:

где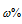 – массовая доля растворённого вещества; m(в-ва) – масса растворённого вещества; m(р-ра) – масса раствора.
– массовая доля растворённого вещества; m(в-ва) – масса растворённого вещества; m(р-ра) – масса раствора.
Тогда

Моляльная концентрация (или моляльность) показывает число молей растворённого вещества, содержащихся в 1000г растворителя.
Находим, сколько граммов CdCl2 содержится в 1000г воды, составив пропорцию:

Теперь рассчитаем моляльность раствора:

Ответ: 53,3%; 6,22 моль/кг.
Источник
Êîíöåíòðàöèÿ ðàñòâîðà ìîæåò âûðàæàòüñÿ êàê â áåçðàçìåðíûõ åäèíèöàõ (äîëÿõ, ïðîöåíòàõ), òàê è â ðàçìåðíûõ âåëè÷èíàõ (ìàññîâûõ äîëÿõ, ìîëÿðíîñòè, òèòðàõ, ìîëüíûõ äîëÿõ).
Êîíöåíòðàöèÿ – ýòî êîëè÷åñòâåííûé ñîñòàâ ðàñòâîðåííîãî âåùåñòâà (â êîíêðåòíûõ åäèíèöàõ) â åäèíèöå îáúåìà èëè ìàññû. Îáîçíà÷èëè ðàñòâîðåííîå âåùåñòâî – Õ, à ðàñòâîðèòåëü – S. ×àùå âñåãî èñïîëüçóþ ïîíÿòèå ìîëÿðíîñòè (ìîëÿðíàÿ êîíöåíòðàöèÿ) è ìîëüíîé äîëè.
Ñïîñîáû âûðàæåíèÿ êîíöåíòðàöèè ðàñòâîðîâ.
1. Ìàññîâàÿ äîëÿ (èëè ïðîöåíòíàÿ êîíöåíòðàöèÿ âåùåñòâà) – ýòî îòíîøåíèå ìàññû ðàñòâîðåííîãî âåùåñòâà m ê îáùåé ìàññå ðàñòâîðà. Äëÿ áèíàðíîãî ðàñòâîðà, ñîñòîÿùåãî èç ðàñòâîð¸ííîãî âåùåñòâà è ðàñòâîðèòåëÿ:
 ,
,
ãäå:
ω – ìàññîâàÿ äîëÿ ðàñòâîðåííîãî âåùåñòâà;
mâ-âà – ìàññà ðàñòâîð¸ííîãî âåùåñòâà;
mð-ðà – ìàññà ðàñòâîðèòåëÿ.
Ìàññîâóþ äîëþ âûðàæàþò â äîëÿõ îò åäèíèöû èëè â ïðîöåíòàõ.
2. Ìîëÿðíàÿ êîíöåíòðàöèÿ èëè ìîëÿðíîñòü – ýòî êîëè÷åñòâî ìîëåé ðàñòâîð¸ííîãî âåùåñòâà â îäíîì ëèòðå ðàñòâîðà V:
 ,
,
ãäå:
C – ìîëÿðíàÿ êîíöåíòðàöèÿ ðàñòâîð¸ííîãî âåùåñòâà, ìîëü/ë (âîçìîæíî òàêæå îáîçíà÷åíèå Ì, íàïðèìåð, 0,2 Ì HCl);
n – êîëè÷åñòâî ðàñòâîðåííîãî âåùåñòâà, ìîëü;
V – îáú¸ì ðàñòâîðà, ë.
Ðàñòâîð íàçûâàþò ìîëÿðíûì èëè îäíîìîëÿðíûì, åñëè â 1 ëèòðå ðàñòâîðà ðàñòâîðåíî 1 ìîëü âåùåñòâà, äåöèìîëÿðíûì – ðàñòâîðåíî 0,1 ìîëÿ âåùåñòâà, ñàíòèìîëÿðíûì – ðàñòâîðåíî 0,01 ìîëÿ âåùåñòâà, ìèëëèìîëÿðíûì – ðàñòâîðåíî 0,001 ìîëÿ âåùåñòâà.
3. Ìîëÿëüíàÿ êîíöåíòðàöèÿ (ìîëÿëüíîñòü) ðàñòâîðà Ñ(x) ïîêàçûâàåò êîëè÷åñòâî ìîëåé n ðàñòâîðåííîãî âåùåñòâà â 1 êã ðàñòâîðèòåëÿ m:
 ,
,
ãäå:
Ñ (x) – ìîëÿëüíîñòü, ìîëü/êã;
n – êîëè÷åñòâî ðàñòâîðåííîãî âåùåñòâà, ìîëü;
mð-ëÿ – ìàññà ðàñòâîðèòåëÿ, êã.
4. Òèòð – ñîäåðæàíèå âåùåñòâà â ãðàììàõ â 1 ìë ðàñòâîðà:
 ,
,
ãäå:
T – òèòð ðàñòâîð¸ííîãî âåùåñòâà, ã/ìë;
mâ-âà – ìàññà ðàñòâîðåííîãî âåùåñòâà, ã;
Vð-ðà – îáú¸ì ðàñòâîðà, ìë.
5. Ìîëüíàÿ äîëÿ ðàñòâîð¸ííîãî âåùåñòâà – áåçðàçìåðíàÿ âåëè÷èíà, ðàâíàÿ îòíîøåíèþ êîëè÷åñòâà ðàñòâîðåííîãî âåùåñòâà n ê îáùåìó êîëè÷åñòâó âåùåñòâ â ðàñòâîðå:
 ,
,
ãäå:
N – ìîëüíàÿ äîëÿ ðàñòâîð¸ííîãî âåùåñòâà;
n – êîëè÷åñòâî ðàñòâîð¸ííîãî âåùåñòâà, ìîëü;
nð-ëÿ – êîëè÷åñòâî âåùåñòâà ðàñòâîðèòåëÿ, ìîëü.
Ñóììà ìîëüíûõ äîëåé äîëæíà ðàâíÿòüñÿ 1:
N(X) + N(S) = 1.
ãäå N(X) – ìîëüíàÿ äîëÿ ðàñòâîðåííîãî âåùåñòâà Õ;
N(S) – ìîëüíàÿ äîëÿ ðàñòâîðåííîãî âåùåñòâà S.
Èíîãäà ïðè ðåøåíèè çàäà÷ íåîáõîäèìî ïåðåõîäèòü îò îäíèõ åäèíèö âûðàæåíèÿ ê äðóãèì:

ω(X) – ìàññîâàÿ äîëÿ ðàñòâîðåííîãî âåùåñòâà, â %;
Ì(Õ) – ìîëÿðíàÿ ìàññà ðàñòâîðåííîãî âåùåñòâà;
ρ= m/(1000V) – ïëîòíîñòü ðàñòâîðà.6. Íîðìàëüíàÿ êîíöåíòðàöèÿ ðàñòâîðîâ (íîðìàëüíîñòü èëè ìîëÿðíàÿ êîíöåíòðàöèÿ ýêâèâàëåíòà) – ÷èñëî ãðàìì-ýêâèâàëåíòîâ äàííîãî âåùåñòâà â îäíîì ëèòðå ðàñòâîðà.
Ãðàìì-ýêâèâàëåíò âåùåñòâà – êîëè÷åñòâî ãðàììîâ âåùåñòâà, ÷èñëåííî ðàâíîå åãî ýêâèâàëåíòó.
Ýêâèâàëåíò – ýòî óñëîâíàÿ åäèíèöà, ðàâíîöåííàÿ îäíîìó èîíó âîäîðîäà â êèñëîòîíî-îñíîâíûõ ðåàêöèÿõ èëè îäíîìó ýëåêòðîíó â îêèñëèòåëüíî – âîññòàíîâèòåëüíûõ ðåàêöèÿõ.
Äëÿ çàïèñè êîíöåíòðàöèè òàêèõ ðàñòâîðîâ èñïîëüçóþò ñîêðàùåíèÿ í èëè N. Íàïðèìåð, ðàñòâîð, ñîäåðæàùèé 0,1 ìîëü-ýêâ/ë, íàçûâàþò äåöèíîðìàëüíûì è çàïèñûâàþò êàê 0,1 í.
 ,
,
ãäå:
ÑÍ – íîðìàëüíàÿ êîíöåíòðàöèÿ, ìîëü-ýêâ/ë;
z – ÷èñëî ýêâèâàëåíòíîñòè;
Vð-ðà – îáú¸ì ðàñòâîðà, ë.
Ðàñòâîðèìîñòü âåùåñòâà S – ìàêñèìàëüíàÿ ìàññà âåùåñòâà, êîòîðàÿ ìîæåò ðàñòâîðèòüñÿ â 100 ã ðàñòâîðèòåëÿ:

Êîýôôèöèåíò ðàñòâîðèìîñòè – îòíîøåíèå ìàññû âåùåñòâà, îáðàçóþùåãî íàñûùåííûé ðàñòâîð ïðè êîíêðåòíîé òåìïåðàòóðå, ê ìàññå ðàñòâîðèòåëÿ:

Источник
Задача 416.
В каком объеме 0,1н. раствора содержится 8г CuSO4?
Решение:
Эквивалентная масса соли равна молекулярной массе данной соли делённой на общую валентность металла, входящего в состав соли:

где
MЭ(В) – молярная масса эквивалента соли, г/моль; М(В) – молярная масса соли; n – коэффициент при атоме металла; A – валентность металла.
Отсюда

Массу 0,1 эквивалента соли CuSO4 находим из пропорции:

8г CuSO4 соответствует 0,1 эквиваленту, значит, эта масс содержится в 1л раствора.
Ответ: 1л.
Задача 417.
Для нейтрализации 30мл 0,1н. раствора щелочи потребовалось 12мл раствора кислоты. Определить нормальность кислоты.
Решение:
Для определения нормальности кислоты используем математическое выражение следствия из закона эквивалентности (так называемое правило пропорциональности):
CЭ(А) .V(A) = CЭ(B) . V(B),
CЭ(А) и CЭ(B) – нормальные концентрации эквивалентов веществ А и В, моль/л; V(A) и V(B) – объёмы растворов веществ А и В.
По условию задачи известны CЭ(щелочи), V(щелочи) и V(кислоты), то нетрудно вычислить СЭ(кислоты) по формуле:

Ответ: 0,25н.
Задача 418.
Найти молярность 36,2%-ного (по массе) раствора НСI, плотность которого 1,18г/мл.
Решение:
Молярная(объёмно-молярная) концентрация показывает число молей растворённого вещества, содержащихся в 1 литре раствора. Масса 1 литра раствора HCl (р = 1,18г/мл) равна 1180г (1000 . 1,18 = 1180).
Массу HCl, содержащуюся в 1 литре раствора рассчитаем по формуле:

где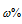 – массовая доля растворённого вещества; m(в-ва) – масса растворённого вещества; m(р-ра) – масса раствора.
– массовая доля растворённого вещества; m(в-ва) – масса растворённого вещества; m(р-ра) – масса раствора.
Тогда

Молярную концентрацию раствора (СМ) получим делением числа граммов HCl в 1л раствора на молярную массу HCl (36,5г/моль):

Ответ: 11,7 моль/л.
Задача 419.
В каком объеме 1М раствора и в каком объеме 1н. раствора содержится 114г Al2(SО4)3?
Решение:
Молярная(объёмно-молярная) концентрация показывает число молей растворённого вещества, содержащихся в 1 литре раствора. Молярная концентрация эквивалента (или нормальность) показывает число эквивалентов растворённого вещества, содержащихся в 1 литре раствора.
M[Al2(SО4)3] = 342 г/моль. Эквивалентная масса соли равна молекулярной массе данной соли делённой на общую валентность металла, входящего в состав соли:

где
MЭ(В) – молярная масса эквивалента соли, г/моль; М(В) – молярная масса соли; n – коэффициент при атоме металла; A – валентность металла.
Отсюда

Находим, в каком объёме 1М раствора содержится 114г Al2(SО4)3 из пропорции:

Теперь находим объём 1н раствора, в котором содержится 114г Al2(SО4)3, составив про-порцию:

Ответ: 0,333л; 2л.
Задача 420.
Растворимость хлорида кадмия при 20°С равна 114,1г в 100г воды. Вычислить массовую долю и моляльность CdCl2 в насыщенном растворе.
Решение:
M(CdCl2) = 183,324г/моль.
Растворимость вещества измеряется содержанием вещества в его насыщенном растворе. Обычно растворимость твёрдых веществ и жидкостей выражают значением коэффициента растворимости, т.е. массой вещества, растворяющегося при данных условиях в 100 г воды или другого растворителя с образованием насыщенного раствора.
m(CdCl2) = 114,1г. m(р-ра) = m(CdCl2) + m(H2O) = 114,1 + 100 = 241,1г.
Массовую долю CdCl2 вычислим по формуле:

где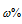 – массовая доля растворённого вещества; m(в-ва) – масса растворённого вещества; m(р-ра) – масса раствора.
– массовая доля растворённого вещества; m(в-ва) – масса растворённого вещества; m(р-ра) – масса раствора.
Тогда

Моляльная концентрация (или моляльность) показывает число молей растворённого вещества, содержащихся в 1000г растворителя.
Находим, сколько граммов CdCl2 содержится в 1000г воды, составив пропорцию:

Теперь рассчитаем моляльность раствора:

Ответ: 53,3%; 6,22 моль/кг.
Источник
Примеры решения задач
1.1. ПРОЦЕНТНАЯ КОНЦЕНТРАЦИЯ
Пример 1
а) Определите массовую долю (%) хлорида калия в растворе, содержащем 0,053 кг KCl в 0,5 л раствора, плотность которого 1063 кг/м3.
Решение:
Массовая доля ω или С% показывает, сколько единиц массы растворенного вещества содержится в 100 единицах массы раствора. Массовая доля – безразмерная величина, ее выражают в долях единицы или процентах:
где ωA – массовая доля (%) растворенного вещества;
mA- масса растворенного вещества, г;
mр-ра – масса раствора, г.
Масса раствора равна произведению объема раствора V на его плотность ρ:
m=ρV, тогда
Массовая доля хлорида калия в растворе равна:
Пример 2
Какой объем раствора азотной кислоты с массовой долей HNO3 30% (ρ=1180кг/м3) требуется для приготовления 20 л 0,5 М раствора этой кислоты?
Решение: Сначала определяем массу азотной кислоты в 20 л 0,5 М раствора:
M (HNO3)=63,01 г/моль;
mHNO3=0,5∙63,01∙20=630,1 г.
Определим, в каком объеме раствора с массовой долей HNO3 30% содержится 630,1 г HNO3 :
Следовательно , чтобы приготовить 20 л 0,5 М HNO3, надо израсходовать всего 1,78 л раствора азотной кислоты с массовой долей HNO3 равной 30%.
Пример 3
Какую массу раствора с массовой долей КОН 20% надо прибавить к 250 г раствора с массовой долей КОН 90%, чтобы получить раствор с ωКОН=50 %?
Решение: Задача решается с помощью правила смешения. Массу раствора с массовой долей КОН 20 % обозначим через х.
Тогда 3х=1000; х=333,3.
Для получения раствора с массовой долей КОН 50 % необходимо к 250 г раствора КОН с ω=90 % прибавить 333,3 г раствора КОН с 20 %.
Задачи такого типа решают с помощью диагональной схемы или «правила креста»: точкой пересечения двух отрезков прямой обозначают свойства смеси, которую необходимо получить.
20 (90-50)=40
50
90 (50-20)=30
Массы исходных растворов, необходимые для приготовления смеси, обратно пропорциональны разностям между концентрациями заданного и менее концентрированного раствора и более концентрированного и заданного растворов:
Также эту задачу можно решить, учитывая, что при сливании двух растворов суммируется масса растворенного вещества. Пусть масса 20% раствора х г, тогда масса КОН в нем 0,2 х. Масса КОН во втором растворе 0,9 · 250 = 225 г. Масса вещества в итоговом растворе 0,5 · (250 + х). Таким образом,
0,2х + 225 = 0,5(250+х); х=333,3 г.
1.2. МОЛЯРНАЯ И ЭКВИВАЛЕНТНАЯ КОНЦЕНТРАЦИИ
Пример 1
Какова масса NaOH, содержащегося в 0,2 л раствора, если молярная концентрация раствора 0,2 моль/л?
Решение:
Молярная концентрация См или М (молярность) показывает количество растворенного вещества, содержащегося в 1 л раствора.
Молярную концентрацию (моль/л) выражают формулой
где m1 – масса растворенного вещества, г;
M – молярная масса растворенного вещества, г/моль;
V – объем раствора, л.
M (NaOН)=40 г/моль. Масса NaOH, содержащегося в растворе, равна
MNaOH=MV=0,2∙40∙0,2=1,6 г.
Пример 2
Определите молярную концентрацию эквивалента хлорида железа (ІІІ), если в 0,3 л раствора содержится 32,44 г FeCl3.
Решение:
Молярная концентрация эквивалента вещества (нормальность) показывает число молярных масс эквивалентов растворенного вещества, содержащихся в 1л раствора (моль/л):
где mА – масса растворенного вещества, г;
M (1/zА) – молярная масса эквивалента растворенного вещества, г/моль;
V – объем раствора, л.
Молярная масса эквивалента FeCl3 равна
Молярная концентрация эквивалента раствора FeCl3 равна
Пример 3
Определите концентрацию раствора КОН, если на нейтрализацию 0,035 л 0,3 н. H3PO4 израсходовано 0,02 л раствора КОН.
Решение:
Из закона эквивалентов следует, что количество эквивалентов веществ участвующих в химической реакции одинаково. В реакции участвуют 0,035·0,3=0,0105 эквивалента фосфорной кислоты. Для нейтрализации H3PO4
потребуется такое же количество вещества эквивалента КОН, т.е.
V(H3PO4)СН(H3PO4)=V(KOH)СН(KOH).
Отсюда
1.3. МОЛЯЛЬНАЯ КОНЦЕНТРАЦИЯ (МОЛЯЛЬНОСТЬ) , МОЛЬНАЯ ДОЛЯ, ТИТР
Пример 1
В какой массе эфира надо растворить 3,04 г анилина C6H5NH2 , чтобы получить раствор, моляльность которого равна 0,3 моль/кг?
Решение:
Моляльность раствора Сm (моль/кг) показывает количество растворенного вещества, находящегося в 1 кг растворителя:
где mр-ля – масса растворителя, кг;
n (А) – количество растворенного вещества, моль.
M (C6H5NH2 ) – 99,13 г/моль.
Масса растворителя (эфира) равна:
тогда
Пример 2
Определите титр 0,01 н. КОН.
Решение:
Титр раствора показывает массу (г) растворенного вещества, содержащегося в 1 мл раствора. В 1 л 0,01 н. КОН содержится 0,564 г КОН. Титр этого раствора равен:
Т= 0,561/1000=0,000561 г/мл.
Пример 3
Рассчитайте молярные доли глюкозы C6H12O6 и воды в растворе с массовой долей глюкозы 36 %.
Решение:
Мольная доля вещества А(χА) в растворе равна отношению количества данного вещества nА к общему количеству всех веществ, содержащихся в растворе:
где ( ) количество всех веществ, содержащихся в растворе.
В 100 г раствора с массовой долей глюкозы, равной 36 %, содержится 36 г глюкозы и 64 г воды:
nC6H12O6 =36/180=0,20 моль;
nH2O= 64/18= 3,56 моль;
nC6H12O6 + nH2O= 0,20 + 3,56 =3,76 моль;
χC6H12O6= 0,20/3,76= 0,053;
χH2O= 3,56/3,76= 0,947.
Сумма молярных долей всех компонентов раствора равна 1.
Пример 4
Вычислите молярную концентрацию эквивалента, молярную концентрацию и моляльность раствора, в котором массовая доля CuSO4 равна 10 %. Плотность раствора 1107 кг/м3.
Решение:
Определим молярную массу и молярную массу эквивалента CuSO4:
M (CuSO4)= 159,61 г/моль; M(1/2 CuSO4)=
В 100 г раствора с ωCuSO4=10 % содержится 10,0 г CuSO4 и 90 г H2O.
Следовательно, моляльность раствора CuSO4 равна
Сm(CuSO4/H2O)=10/(159,61∙0,09)=0,696 моль/кг.
Молярная концентрация и молярная концентрация эквивалента относятся к 1л раствора:
mр-ра= ρV= 1107·10-3=1,107 кг.
В этой массе раствора содержится 1,107·0,1=0,1107 кг CuSO4, что составляет 110,7/159,61=0,693 моль, или 0,693·2=1,386 экв.
Молярная концентрация и молярная концентрация эквивалента данного раствора соответственно равны 0,693 и 1,386 моль/л.
1.4. ОСМОТИЧЕСКОЕ ДАВЛЕНИЕ. ЗАКОН ВАНТ- ГОФФА
Пример 1
Вычисление осмотического давления растворов.
Вычислите осмотическое давление раствора, содержащего в
1,4 л 63 г глюкозы С6Н12О6 при 0°С.
Решение:
Осмотическое давление раствора определяют согласно закону Вант-Гоффа:
Pocм = nRT/V,
где п — количество растворенного вещества, моль;
V – объем раствора, м3;
R — молярная газовая постоянная, равная 8,3144 Дж/(моль-К).
В 1,4 л раствора содержится 63 г глюкозы, молярная масса которой равна 180,16 г/моль. Следовательно, в 1,4л раствора содержится
n= 63/180,16=0,35моль глюкозы.
Осмотическое давление этого раствора глюкозы:
Пример 2
Определение молекулярной массы неэлектролита по осмотическому давлению раствора.
Рассчитайте молекулярную массу неэлектролита, если в 5л раствора содержится 2,5 г неэлектролита. Осмотическое давление этого раствора равно 0,23∙105 Па при 20°С.
Решение:
Заменив п выражением m/M, где т — масса растворенного вещества, а М — его молярная масса, получим
Росм = mRT/(MV).
Отсюда молярная масса растворенного вещества равна
Следовательно, молекулярная масса неэлектролита равна 52,96
Росм кПа: R=8,31 Дж/моль∙К;
Росм мм Hg ст.: R=62,32 л∙мм.рт.ст./град.∙моль;
Росм. атм.: R=0,082 л∙атм../град.∙моль.
1.5.ДАВЛЕНИЕ НАСЫЩЕННОГО ПАРА РАСТВОРОВ. ТОНОМЕТРИЧЕСКИЙ ЗАКОН РАУЛЯ
Пример 1. а) Вычислите давление пара над раствором, содержащим 34,23 г сахара C12H22O11 в 45,05 г воды при 65 ºС, если давление паров воды при этой температуре равно 2,5·104 Па.
Решение:
Давление пара над раствором нелетучего вещества в растворителе всегда ниже давления пара над чистым растворителем при той же температуре. Относительное понижение давления пара растворителя над раствором согласно закону Рауля выражается соотношением
где p0 – давление пара над чистым растворителем;
p – давление пара растворителя над раствором;
n – количество растворенного вещества, моль;
N – количество растворителя, моль;
M (C12H22O11) = 342,30 г/моль;
M (H2O) = 18,02 г/моль.
Количество растворенного вещества и растворителя: n=34,23/342,30=0,1 моль; N = 45,05/18,02= 2,5моль.
Давление пара над раствором:
Пример 2. Рассчитайте молекулярную массу неэлектролита, если 28,5 г этого вещества, растворенного в 785 г воды, вызывают понижение давления пара воды над раствором на 52,37 Па при 40°С. Давление водяного пара при этой температуре равно 7375,9 Па.
Решение:
Относительное понижение давления пара растворителя над раствором равно
Находим:
здесь mx – масса неэлектролита, молярная масса которого Mx г/моль.
0,309Mx + 0,202=28,5;
0,309Mx =28,298;
Mx=91,58 г/моль.
Молекулярная масса неэлектролита равна ~ 92.
1.6. ТЕМПЕРАТУРЫ КИПЕНИЯ И ЗАМЕРЗАНИЯ РАСТВОРОВ.
ЭБУЛЛИОСКОПИЧЕСКИЙ И КРИОСКОПИЧЕСКИЙ ЗАКОНЫ РАУЛЯ
Пример 1.Определите температуру кипения и замерзания раствора, содержащего 1 г нитробензола C6H5NO2 в 10 г бензола. Эбулиоскопическая и криоскопическая константы равны 2,57 и 5,1 °С. Температура кипения чистого бензола 80,2 °С, температура замерзания –5,4°С.
Решение:
По закону Рауля:
где ∆tзам и ∆tкип – соответственно понижение температуры замерзания и повышение температуры кипения раствора; Кк и Кэ – соответственно криоскопическая и эбуллиоскопическая константы растворителя; g- масса растворенного вещества, г; G- масса растворителя, г; Мr- молекулярная масса растворенного вещества; Mr(С6H5NO2)= 123,11.
Повышение температуры кипения раствора нитробензола в бензоле:
Температура кипения раствора: tкип=80,2+2,09=82,29 °C.
Понижение температуры замерзания раствора нитробензола в бензоле:
Температура замерзания раствора tзам= 5,4 – 4,14 =1,26 °C.
Пример 2.Раствор камфоры массой 0,522 г в 17 г эфира кипит при температуре на 0,461ºС выше, чем чистый эфир. Эбуллиоскопическая константа эфира 2,16 ºС. Определите молекулярную массу камфоры.
Решение:
Молекулярную массу камфоры определяем, пользуясь соотношением
Mr=
Молекулярная масса камфоры равна 155,14.
Читайте также:
Рекомендуемые страницы:
©2015-2020 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2016-07-22
Нарушение авторских прав и Нарушение персональных данных
Источник
