Какой четырехугольник называется прямоугольником свойства прямоугольника

В школьной программе на уроках геометрии приходится иметь дело с разнообразными видами четырёхугольников: ромбами, параллелограммами, прямоугольниками, трапециями, квадратами. Самыми первыми фигурами для изучения становятся прямоугольник и квадрат.
Итак, что же такое прямоугольник? Определение для 2 класса общеобразовательной школы будет выглядеть так: это четырёхугольник, у которого все четыре угла прямые. Несложно представить себе, как выглядит прямоугольник: это фигура с 4 прямыми углами и сторонами, попарно параллельными друг другу.
…
Признаки и свойства прямоугольника
Как понять, решая очередную геометрическую задачу, с каким именно четырёхугольником мы имеем дело? Существуют три основных признака, по которым можно безошибочно определить, что речь идёт именно о прямоугольнике. Назовём их:
- фигура является четырёхугольником, три угла которого равны 90°;
- представленный четырёхугольник — это параллелограмм с равными диагоналями;
- параллелограмм, который имеет по крайней мере один прямой угол.
Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.
Поскольку прямоугольник — это параллелограмм (т. е. четырёхугольник с попарно параллельными противоположными сторонами), то для него будут выполняться все его свойства и признаки.
Формулы для вычисления длины сторон
В прямоугольнике противолежащие стороны равны и взаимно параллельны. Более длинную сторону принято называть длиной (обозначается a), более короткую — шириной (обозначается b). В прямоугольнике на изображении длинами являются стороны AB и CD, а шириной — AC и B. D. Также они перпендикулярны к основаниям (т. е. являются высотами).
Это интересно: в геометрии луч — это что такое, основное понятие.
Для нахождения сторон можно воспользоваться формулами, указанными ниже. В них приняты условные обозначения: a — длина прямоугольника, b — его ширина, d — диагональ (отрезок, соединяющий вершины двух углов, лежащих друг напротив друга), S — площадь фигуры, P — периметр, α — угол между диагональю и длиной, β — острый угол, который образован обеими диагоналями. Способы нахождения длин сторон:
- С использованием диагонали и известной стороны: a = √(d ² — b ²), b = √(d ² — a ²).
- По площади фигуры и одной из её сторон: a = S / b, b = S / a.
- При помощи периметра и известной стороны: a = (P — 2 b) / 2, b = (P — 2 a) / 2.
- Через диагональ и угол между ней и длиной: a = d sinα, b = d cosα.
- Через диагональ и угол β: a = d sin 0,5 β, b = d cos 0,5 β.
Это интересно: как сравнить два отрезка — способы с примерами.
Периметр и площадь
Периметром четырёхугольника называют сумму длин всех его сторон. Чтобы вычислить периметр, могут использоваться следующие формулы:
- Через обе стороны: P = 2 (a + b).
- Через площадь и одну из сторон: P = (2S + 2a ²) / a, P = (2S + 2b ²) / b.
Площадь — это пространство, ограниченное периметром. Три основных способа для расчёта площади:
- Через длины обеих сторон: S = a*b.
- При помощи периметра и какой-либо одной известной стороны: S = (Pa — 2 a ²) / 2; S = (Pb — 2 b ²) / 2.
- По диагонали и углу β: S = 0,5 d ² sinβ.
Диагонали прямоугольника
В задачах школьного курса математики часто требуется хорошо владеть свойствами диагоналей прямоугольника. Перечислим основные из них:
- Диагонали равны друг другу и делятся на два равных отрезка в точке их пересечения.
- Диагональ определяется как корень суммы обеих сторон, возведённых в квадрат (следует из теоремы Пифагора).
- Диагональ разделяет прямоугольник на два треугольника с прямым углом.
- Точка пересечения совпадает с центром описанной окружности, а сами диагонали — с её диаметром.
Это интересно: как обозначается площадь, примеры для вычисления.
Применяются следующие формулы для расчёта длины диагонали:
- С использованием длины и ширины фигуры: d = √(a ² + b ²).
- С использованием радиуса окружности, описанной вокруг четырёхугольника: d = 2 R.
Определение и свойства квадрата
Квадрат — это частный случай ромба, параллелограмма или прямоугольника. Его отличие от этих фигур заключается в том, что все его углы прямые, и все четыре стороны равны. Квадрат — это правильный четырёхугольник.
Четырёхугольник называют квадратом в следующих случаях:
- Если это прямоугольник, у которого длина a и ширина b равны.
- Если это ромб с равными длинами диагоналей и с четырьмя прямыми углами.
К свойствам квадрата относятся все ранее рассмотренные свойства, относящиеся к прямоугольнику, а также следующие:
- Диагонали перпендикулярны относительно друг друга (свойство ромба).
- Точка пересечения совпадает с центром вписанной окружности.
- Обе диагонали делят четырёхугольник на четыре одинаковых прямоугольных и равнобедренных треугольника.
Приведём часто используемые формулы для вычисления периметра, площади и элементов квадрата:
- Диагональ d = a √2.
- Периметр P = 4 a.
- Площадь S = a ².
- Радиус описанной окружности вдвое меньше диагонали: R = 0,5 a √2.
- Радиус вписанной окружности определяется как половинная длина стороны: r = a / 2.
Примеры вопросов и задач
Разберём некоторые вопросы, с которыми можно столкнуться при изучении курса математики в школе, и решим несколько простых задач.
Задача 1. Как изменится площадь прямоугольника, если увеличить длину его сторон в три раза?
Решение: Обозначим площадь исходной фигуры S0, а площадь четырёхугольника с утроенной длиной сторон — S1. По формуле, рассмотренной ранее, получаем: S0 = ab. Теперь увеличим длину и ширину в 3 раза и запишем: S1= 3 a • 3 b = 9 ab. Сравнивая S0 и S1, становится очевидно, что вторая площадь больше первой в 9 раз.
Вопрос 1. Четырёхугольник с прямыми углами — это квадрат?
Решение: Из определения следует, что фигура с прямыми углами является квадратом лишь тогда, когда длины всех его сторон равны. В остальных случаях фигура является прямоугольником.
Задача 2. Диагонали прямоугольника образуют угол 60 градусов. Ширина прямоугольника — 8. Рассчитать, чему равна диагональ.
Решение: Вспомним, что диагонали точкой пересечения разделяются пополам. Таким образом, имеем дело с равнобедренным треугольником с углом при вершине, равным 60°. Так как треугольник равнобедренный, то находящиеся при основании углы тоже будут одинаковы. Путём несложных вычислений получаем, что каждый из них равен 60°. Отсюда следует, что треугольник равносторонний. Ширина, известная нам, является основанием треугольника, следовательно, половина диагонали тоже равна 8, а длина целой диагонали в два раза больше и равна 16.
Вопрос 2. У прямоугольника все стороны равны или нет?
Решение: Достаточно вспомнить, что все стороны должны быть равны у квадрата, который является частным случаем прямоугольника. Во всех остальных случаях достаточное условие — это наличие минимум 3 прямых углов. Равенство сторон не является обязательным признаком.
Задача 3. Площадь квадрата известна и равна 289. Найти радиусы вписанной и описанной окружности.
Решение: По формулам для квадрата проведём следующие расчёты:
- Определим, чему равны основные элементы квадрата: a = √ S = √289 = 17; d = a √2 =1 7√2.
- Подсчитаем, чему равен радиус описанной вокруг четырёхугольника окружности: R = 0,5 d = 8,5√2.
- Найдём радиус вписанной окружности: r = a / 2 = 17 / 2 = 8,5.
Источник
 В школьной программе на уроках геометрии приходится иметь дело с разнообразными видами четырёхугольников: ромбами, параллелограммами, прямоугольниками, трапециями, квадратами. Самыми первыми фигурами для изучения становятся прямоугольник и квадрат.
В школьной программе на уроках геометрии приходится иметь дело с разнообразными видами четырёхугольников: ромбами, параллелограммами, прямоугольниками, трапециями, квадратами. Самыми первыми фигурами для изучения становятся прямоугольник и квадрат.
Итак, что же такое прямоугольник? Определение для 2 класса общеобразовательной школы будет выглядеть так: это четырёхугольник, у которого все четыре угла прямые. Несложно представить себе, как выглядит прямоугольник: это фигура с 4 прямыми углами и сторонами, попарно параллельными друг другу.
Признаки и свойства прямоугольника
Как понять, решая очередную геометрическую задачу, с каким именно четырёхугольником мы имеем дело? Существуют три основных признака, по которым можно безошибочно определить, что речь идёт именно о прямоугольнике. Назовём их:
- фигура является четырёхугольником, три угла которого равны 90°,
- представленный четырёхугольник — это параллелограмм с равными диагоналями,
- параллелограмм, который имеет по крайней мере один прямой угол.
Интересно знать: что такое выпуклый четырехугольник, его особенности и признаки.
Поскольку прямоугольник — это параллелограмм (т. е. четырёхугольник с попарно параллельными противоположными сторонами), то для него будут выполняться все его свойства и признаки.
Формулы для вычисления длины сторон
В прямоугольнике противолежащие стороны равны и взаимно параллельны. Более длинную сторону принято называть длиной (обозначается a), более короткую — шириной (обозначается b). В прямоугольнике на изображении длинами являются стороны AB и CD, а шириной — AC и B. D. Также они перпендикулярны к основаниям (т. е. являются высотами).
Это интересно: в геометрии луч это что такое, основное понятие.
Для нахождения сторон можно воспользоваться формулами, указанными ниже. В них приняты условные обозначения: a — длина прямоугольника, b — его ширина, d — диагональ (отрезок, соединяющий вершины двух углов, лежащих друг напротив друга), S — площадь фигуры, P — периметр, α угол между диагональю и длиной, β острый угол, который образован обеими диагоналями. Способы нахождения длин сторон:
- С использованием диагонали и известной стороны: a = √(d ² b ²), b = √(d ² a ²).
- По площади фигуры и одной из её сторон: a = S / b, b = S / a.
- При помощи периметра и известной стороны: a = (P — 2 b) / 2, b = (P — 2 a) / 2.
- Через диагональ и угол между ней и длиной: a = d sinα, b = d cosα.
- Через диагональ и угол β: a = d sin 0,5 β, b = d cos 0,5 β.
Это интересно: как сравнить два отрезка способы с примерами.
Периметр и площадь
 Периметром четырёхугольника называют сумму длин всех его сторон. Чтобы вычислить периметр, могут использоваться следующие формулы:
Периметром четырёхугольника называют сумму длин всех его сторон. Чтобы вычислить периметр, могут использоваться следующие формулы:
- Через обе стороны: P = 2 (a + b).
- Через площадь и одну из сторон: P = (2S + 2a ²) / a, P = (2S + 2b ²) / b.
Площадь — это пространство, ограниченное периметром. Три основных способа для расчёта площади:
- Через длины обеих сторон: S = a*b.
- При помощи периметра и какой-либо одной известной стороны: S = (Pa — 2 a ²) / 2, S = (Pb — 2 b ²) / 2.
- По диагонали и углу β: S = 0,5 d ² sinβ.
Диагонали прямоугольника
В задачах школьного курса математики часто требуется хорошо владеть свойствами диагоналей прямоугольника. Перечислим основные из них:
- Диагонали равны друг другу и делятся на два равных отрезка в точке их пересечения.
- Диагональ определяется как корень суммы обеих сторон, возведённых в квадрат (следует из теоремы Пифагора).
- Диагональ разделяет прямоугольник на два треугольника с прямым углом.
- Точка пересечения совпадает с центром описанной окружности, а сами диагонали — с её диаметром.
Это интересно: как обозначается площадь, примеры для вычисления.
Применяются следующие формулы для расчёта длины диагонали:
- С использованием длины и ширины фигуры: d = √(a ² + b ²).
- С использованием радиуса окружности, описанной вокруг четырёхугольника: d = 2 R.
Определение и свойства квадрата
Квадрат — это частный случай ромба, параллелограмма или прямоугольника. Его отличие от этих фигур заключается в том, что все его углы прямые, и все четыре стороны равны. Квадрат — это правильный четырёхугольник.
Четырёхугольник называют квадратом в следующих случаях:
- Если это прямоугольник, у которого длина a и ширина b равны.
- Если это ромб с равными длинами диагоналей и с четырьмя прямыми углами.
К свойствам квадрата относятся все ранее рассмотренные свойства, относящиеся к прямоугольнику, а также следующие:
- Диагонали перпендикулярны относительно друг друга (свойство ромба).
- Точка пересечения совпадает с центром вписанной окружности.
- Обе диагонали делят четырёхугольник на четыре одинаковых прямоугольных и равнобедренных треугольника.
Приведём часто используемые формулы для  вычисления периметра, площади и элементов квадрата:
вычисления периметра, площади и элементов квадрата:
- Диагональ d = a √2.
- Периметр P = 4 a.
- Площадь S = a ².
- Радиус описанной окружности вдвое меньше диагонали: R = 0,5 a √2.
- Радиус вписанной окружности определяется как половинная длина стороны: r = a / 2.
Примеры вопросов и задач
Разберём некоторые вопросы, с которыми можно столкнуться при изучении курса математики в школе, и решим несколько простых задач.
Задача 1. Как изменится площадь прямоугольника, если увеличить длину его сторон в три раза?
Решение: Обозначим площадь исходной фигуры S0, а площадь четырёхугольника с утроенной длиной сторон — S1. По формуле, рассмотренной ранее, получаем: S0 = ab. Теперь увеличим длину и ширину в 3 раза и запишем: S1= 3 a • 3 b = 9 ab. Сравнивая S0 и S1, становится очевидно, что вторая площадь больше первой в 9 раз.
Вопрос 1. Четырёхугольник с прямыми углами — это квадрат?
Решение: Из определения следует, что фигура с прямыми углами является квадратом лишь тогда, когда длины всех его сторон равны. В остальных случаях фигура является прямоугольником.
Задача 2. Диагонали прямоугольника образуют угол 60 градусов. Ширина прямоугольника — 8. Рассчитать, чему равна диагональ.
Решение: Вспомним, что диагонали точкой пересечения разделяются пополам. Таким образом, имеем дело с равнобедренным треугольником с углом при вершине, равным 60°. Так как треугольник равнобедренный, то находящиеся при основании углы тоже будут одинаковы. Путём несложных вычислений получаем, что каждый из них равен 60°. Отсюда следует, что треугольник равносторонний. Ширина, известная нам, является основанием треугольника, следовательно, половина диагонали тоже равна 8, а длина целой диагонали в два раза больше и равна 16.
Вопрос 2. У прямоугольника все стороны равны или нет?
Решение: Достаточно вспомнить, что все стороны должны быть равны у квадрата, который является частным случаем прямоугольника. Во всех остальных случаях достаточное условие — это наличие минимум 3 прямых углов. Равенство сторон не является обязательным признаком.
Задача 3. Площадь квадрата известна и равна 289. Найти радиусы вписанной и описанной окружности.
 Решение: По формулам для квадрата проведём следующие расчёты:
Решение: По формулам для квадрата проведём следующие расчёты:
- Определим, чему равны основные элементы квадрата: a = √ S = √289 = 17, d = a √2 =1 7√2.
- Подсчитаем, чему равен радиус описанной вокруг четырёхугольника окружности: R = 0,5 d = 8,5√2.
- Найдём радиус вписанной окружности: r = a / 2 = 17 / 2 = 8,5.
Источник
19 октября 2019
- Прямоугольник — это…
- Его признаки
- Диагональ прямоугольника
- Свойства фигуры
- Периметр и площадь
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.
Название это весьма говорящее, и в нем скрыто официальное определение.
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.
Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.
Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».
Прямоугольник — это…
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).
У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.
То есть выглядит это так:
Так вот, прямоугольник в данном случае является частным случаем параллелограмма.
Судите сами:
У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.
У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.
Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.
Признаки прямоугольника
Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.
В случае с прямоугольником их всего три:
- Если один из углов параллелограмма прямой, то данный параллелограмм является прямоугольником.
- Если три угла четырехугольника являются прямыми, то перед нами опять же прямоугольник. При этом нет необходимости доказывать, что четырехугольник является параллелограммом. Это промежуточное звено становится верно само по себе.
- Если диагонали параллелограмма равны между собой, то фигура точно является прямоугольником.
Диагонали прямоугольника
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».
В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:
Свойства прямоугольника
К свойствам прямоугольника относятся следующие утверждения:
- Прямоугольник является параллелограммом, а значит имеет все присущие ему свойства.
- У прямоугольника равны противоположные стороны.
- У прямоугольника противоположные стороны параллельны.
- У прямоугольников все прилегающие друг к другу стороны пересекаются под прямыми углами. А в сумме они дают 360 градусов.
- У прямоугольников обе диагонали равны между собой.
- Диагональ прямоугольника делит фигуру ровно пополам, и в результате получаются два одинаковых прямоугольных треугольника.
- Диагонали прямоугольника пересекаются в его геометрическом центре. А их точка пересечения делит каждую диагональ на два равных отрезка. Более того, все четыре отрезка равны между собой.
- У прямоугольника точка пересечения диагоналей является еще и центром описанной вокруг окружности. Причем длина диагонали одновременна является диаметром (что это такое?) этой окружности.
Периметр и площадь
Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.
Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:
Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:
К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.
Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.
Источник
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)
Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Виды четырехугольников: | |||
| |||
| |||
| |||
| |||
|  | ||
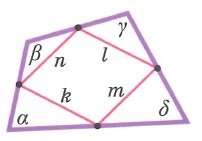
Свойства произвольных четырехугольников: | |||
|  | ||
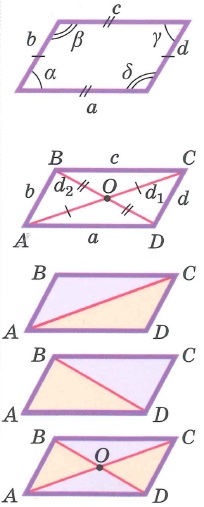
Свойства параллелограмма: | |||
|  | ||
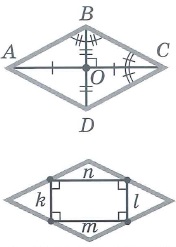
Свойства ромба: | |||
|  | ||
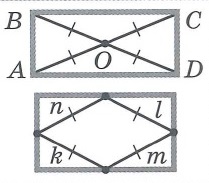
Свойства прямоугольника: | |||
|  | ||
Свойства квадрата: | |||
| |||
Свойства трапеции: | |||
| 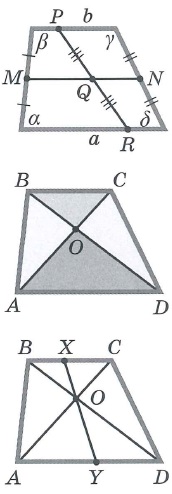 | ||
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
Источник
