Какого вида параллелепипед обладает свойствами

Что такое параллелепипед?
Что за слово такое мудреное – «параллелепипед»?
Что за многогранник скрывается за этим словом?
Что-то должно быть связано с параллельностью, не правда ли?
Так и есть. Читай статью и ты все поймешь!
Параллелепипед – многоугольник, образованный пересечением трех пар параллельных плоскостей.
Если слишком сложно, просто посмотри на картинку.
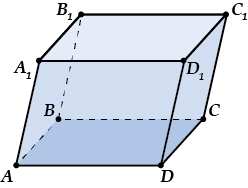
Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?
Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.

Смотри, запоминай и не путай!
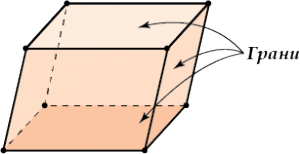

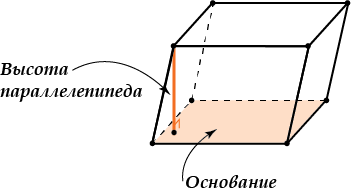

Высота – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Та грань, на которую опущена высота, называется основанием.
- Все грани параллелепипеда – параллелограммы.
- Противоположные грани параллелепипеда параллельны и равны.
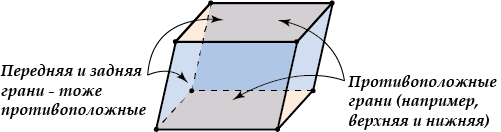
Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, асмежные.
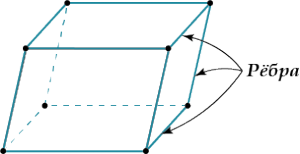
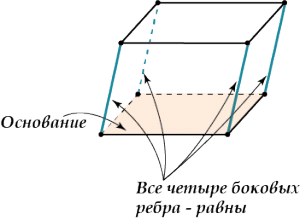
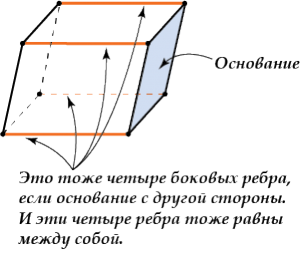
- Боковые ребра параллелепипеда равны.
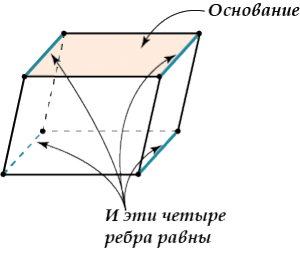
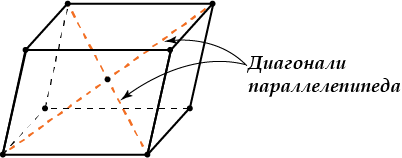
- Диагонали параллелепипеда пересекаются и точкой пересечения делятся пополам.
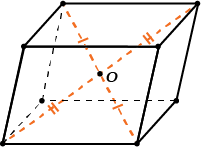
Точка пересечения диагоналей называется центром параллелепипеда.
Прямым называется параллелепипед, у которого боковые ребра перпендикулярны основанию.
Вот так:
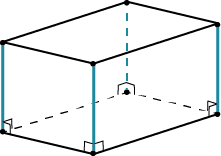
У прямого параллелепипеда в основании – параллелограмм, а боковые грани – прямоугольники.
Прямоугольным называется параллелепипед, у которого в основании прямоугольник, а боковые ребра перпендикулярны основанию.
Это такая обувная коробка:
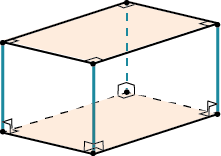
У прямоугольного параллелепипеда все грани – прямоугольники.
Давай-ка теперь выведем одну интересную формулу для диагонали прямоугольного параллелепипеда.

Диагональ прямоугольного параллелепипеда равна сумме квадратов его измерений.
( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}).
Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.
Смотри:
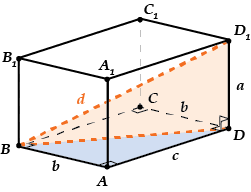
( displaystyle Delta BAD) – прямоугольный, поэтому
( displaystyle B{{D}^{2}}=A{{B}^{2}}+A{{D}^{2}}={{b}^{2}}+{{c}^{2}})
( displaystyle Delta BD{{D}_{1}}) – тоже прямоугольный!
Поэтому
( displaystyle B{{D}_{1}}^{2}=B{{D}^{2}}+D{{D}_{1}}^{2}),
Подставим:
( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}})
Вывели формулу.
Куб – параллелепипед, у которого все грани квадраты.

Все ребра куба равны.
Кстати, заметь, что куб – частный вид прямоугольного параллелепипеда.
Поэтому для диагонали куба действует формула, которую мы получили для прямоугольного параллелепипеда.
( displaystyle {{d}^{2}}={{a}^{2}}+{{a}^{2}}+{{a}^{2}}),
То есть
( displaystyle d=asqrt{3})
Давай убедимся в пользе этой формулы.
Представь, что у тебя задача: «Диагональ куба равна ( displaystyle 5sqrt{3}). Найти полную поверхность».
Решим ее.
Это закрытый контент
Оставьте E-mail и получите доступ к нему
Пользуясь нашей формулой: ( displaystyle d=asqrt{3}), мы узнали, что ( displaystyle 5sqrt{3}=asqrt{3} ), то есть ( displaystyle a=5).
Значит полная поверхность – шесть площадей квадратов со стороной ( displaystyle a) -равна:
( displaystyle S=6cdot {{a}^{2}}=6cdot 25=150).
Видишь, как быстро? И ты применяй!
Определения:

Параллелепипед — это четырехугольная призма (многогранник с ( displaystyle 6) гранями), все грани которой — параллелограммы.

Прямой параллелепипед — это параллелепипед, у которого ( displaystyle 4) боковые грани — прямоугольники.

Прямоугольный параллелепипед — параллелепипед, у которого все грани – прямоугольники

Куб — параллелепипед, у которого все грани квадраты.
Высота параллелепипеда – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Свойства:
- Противолежащие грани параллелепипеда параллельны и равны.
- Диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
- Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через точку пересечения диагоналей (центр параллелепипеда), делится ею пополам.
- Все диагонали прямоугольного параллелепипеда равны между собой и равны сумме квадратов его измерений.
( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}).

P.S. Последний бесценный совет ????
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
- проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
- подтянуть слабые места с помощью видеоуроков, вебинаров;
- понять тему с помощью статей учебника YouClever;
- набить руку, решая задачи и получая проверку и решения;
- сдать пробный ЕГЭ и получить сразу оценку и разбор ошибок.
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Время услышать тебя!
Теперь ты знаешь все про параллелепипед и куб. Ты воспользуешься этим в решении многих задач стереометрии!
Считай, ты помог себе из будущего ????
А теперь мы хотим услышать тебя. Напиши в комментариях ниже свое мнение об этой статье!
Помогла ли она тебе? Все ли было понятно?
А еще ты можешь задать любой вопрос. Мы ответим!
Успехов!
Источник
Тетраэдр. Виды тетраэдров
Тетраэдр (четырёхгранник) — многогранник, гранями которого являются четыре треугольника (от греческого tetra — четыре и hedra — грань).
Рис. 1
У тетраэдра (4) грани, (4) вершины и (6) рёбер (Рис. 1).
Один из треугольников называется основанием тетраэдра, а три остальные — боковыми гранями тетраэдра.
В зависимости от видов треугольников и их расположения выделяют разные виды тетраэдров.
В школьном курсе чаще говорят о следующих видах тетраэдра:
– равногранный тетраэдр, у которого все грани — равные между собой треугольники;
– правильная треугольная пирамида — основание — равносторонний треугольник, все боковые грани — одинаковые равнобедренные треугольники (Рис. 3);
– правильный тетраэдр, у которого все четыре грани — равносторонние треугольники (Рис. 2).
Рис. 2 Рис. 3
Свойство правильного тетраэдра:
из определения правильного многогранника следует, что все рёбра тетраэдра имеют равную длину, а грани — равную площадь.
Параллелепипед. Виды параллелепипедов
Параллелепипедом называется многогранник, у которого (6) граней — параллелограммы.
Рис. 4
У параллелепипеда, как отмечено, (6) граней, (8) вершин и (12) рёбер (Рис. 4).
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих рёбер — противоположными.
Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани — боковыми гранями параллелепипеда.
Рёбра параллелепипеда, не принадлежащие основаниям, называют боковыми рёбрами.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда (Рис. 5).
Рис. 5
В зависимости от видов параллелограммов и их расположения выделяют разные виды параллелепипедов:
параллелепипеды могут быть прямые и наклонные.
У прямых параллелепипедов боковые грани — прямоугольники (Рис. 5),
у наклонных — параллелограммы (Рис. 4).
Прямой параллелепипед, у которого основанием тоже является прямоугольник, называется прямоугольным параллелепипедом.
Рис. 6
Длины непараллельных рёбер прямоугольного параллелепипеда называются его линейными размерами (измерениями).
У прямоугольного параллелепипеда — три линейных размера: DA, DC, DD1 (Рис. 6).
Свойства параллелепипеда:
– противоположные грани параллелепипеда равны и параллельны.
– Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
– Боковые грани прямого параллелепипеда — прямоугольники.
Построение сечения тетраэдра и параллелепипеда
Плоскостью сечения многогранника можно назвать любую плоскость, по обе стороны которой находятся точки многогранника.
Секущая плоскость пересекает грани многогранников по отрезкам.
Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Так как у тетраэдра (4) грани, то сечением тетраэдра может быть треугольник (Рис. 7) или
четырёхугольник (Рис. 8).
Рис. 7 Рис. 8
У параллелепипеда (6) граней, поэтому сечением этого многогранника может быть треугольник (Рис. 9), четырёхугольник ( Рис. 10), пятиугольник (Рис. 11) или шестиугольник (Рис. 12).
При построении сечения надо вспомнить следующие знания из предыдущих тем:
1. если две точки прямой принадлежат плоскости, то прямая находится в этой плоскости.
2. Если две плоскости имеют общую точку, то эти плоскости пересекаются по прямой.
3. Если плоскость пересекает две параллельные плоскости, то линии пересечения параллельны.
Пример:
Задача
Построить сечение параллелепипеда плоскостью, которая проходит через точки (K), (M) и (N).
1. Проводим (MK), так как обе точки находятся в одной плоскости;
2. MK∩CC1=X — непараллельные прямые в одной плоскости пересекаются;
3. проводим (XN), так как обе точки находятся в одной плоскости;
4. XN∩D1C1=P;
5. проводим (MP), так как обе точки находятся в одной плоскости;
6. через точку (N) в плоскости основания NL∥MP, так как линии пересечения параллельных плоскостей с третьей плоскостью должны быть параллельны;
7. соединяем (N) и (L) и получаем сечение (MPNLK).
Источник
Параллелепипед – это геометрическая фигура, все 6 граней которой представляют собой параллелограммы.

В зависимости от вида этих параллелограммов различают следующие виды параллелепипеда:
- прямой;
- наклонный;
- прямоугольный.
Прямым параллелепипедом называют четырехугольную призму, ребра которой составляют с плоскостью основания угол 90 °.
Прямоугольным параллелепипедом называют четырехугольную призму, все грани которой являются прямоугольниками. Куб есть разновидность четырехугольной призмы, у которой все грани и ребра равны между собой.
Свойства параллелепипеда
Особенности фигуры предопределяют ее свойства. К ним относят 4 следующих утверждений:
- Противолежащие ребра и грани фигуры параллельны и равны между собой.

- Углы сонаправленных сторон равны между собой. На фотографии ниже представлено графическое изображение сонапрвленных лучей OA и O1А1. Прямая рассекает пространство на две плоскости. Если лучи расположены в одной полуплоскости и параллельны друг другу, то их называют сонаправленными.

- 4 главные диагонали параллелепипеда пересекаются в одной точке внутри фигуры. Любой отрезок, проведенный между двумя плоскостями граней, через данную точку будет поделен ею пополам. Следствием данного свойства можно сформулировать следующим образом: плоскости, в которых лежат главные диагонали параллелепипеда, симметрично делят геометрическое тело.

- Согласно теореме Пифагора, квадрат диагонали параллелепипеда равен сумме квадратов ее измерений.

Запомнить все приведенные свойства просто, они легки для понимания и выводятся логически исходя из вида и особенностей геометрического тела. Однако, незамысловатые утверждения могут быть невероятно полезны при решении типовых заданий ЕГЭ и позволят сэкономить время необходимое для прохождения теста.
Формулы параллелепипеда
Для поиска ответов на поставленную задачу недостаточно знать только свойства фигуры. Также могут понадобиться и некоторые формулы для нахождения площади и объема геометрического тела.

Площадь оснований находится также как и соответствующий показатель параллелограмма или прямоугольника. Выбирать основание параллелограмма можно самостоятельно. Как правило, при решении задач проще работать с призмой, в основании которой лежит прямоугольник.
Формула нахождения боковой поверхности параллелепипеда, также может понадобиться в тестовых заданиях.

Примеры решения типовых заданий ЕГЭ
Задание 1.
Дано: прямоугольный параллелепипед с измерениями 3, 4 и 12 см.
Необходимо найти длину одной из главных диагоналей фигуры.
Решение: Любое решение геометрической задачи должно начинаться с построения правильного и четкого чертежа, на котором будет обозначено «дано» и искомая величина. На рисунке ниже приведен пример правильного оформления условий задания.

Рассмотрев сделанный рисунок и вспомнив все свойства геометрического тела, приходим к единственно верному способу решения. Применив 4 свойство параллелепипеда, получим следующее выражение:

После несложных вычислений получим выражение b2=169, следовательно, b=13. Ответ задания найден, на его поиск и чертеж необходимо потратить не более 5 минут.
Задание 2.
Дано: наклонный параллелепипед с боковым ребром 10 см, прямоугольник KLNM с измерениями 5 и 7 см, являющийся сечением фигуры параллельным указанному ребру.
Необходимо найти площадь боковой поверхности четырехугольной призмы.
Решение: Сначала необходимо зарисовать дано.

Для решения данного задания необходимо применить смекалку. Из рисунка видно, что стороны KL и AD – неравны, как и пара ML и DC. Однако, периметры данных параллелограммов очевидно равны.
Следовательно, боковая площадь фигуры будет равна площади сечения помноженной на ребро AA1, так как по условию ребро перпендикулярно сечению. Ответ: 240 см2.
Похожие статьи
Источник
Ïàðàëëåëåïèïåä — ïðèçìà, îñíîâàíèåì êîòîðîé ÿâëÿåòñÿ ïàðàëëåëîãðàìì ëèáî (ðàâíîñèëüíî) ìíîãîãðàííèê ñ øåñòüþ ãðàíÿìè, ÿâëÿþùèìèñÿ ïàðàëëåëîãðàììàìè. Øåñòèãðàííèê.
Ïàðàëëåëîãðàììû, èç êîòîðûõ ñîñòîèò ïàðàëëåëåïèïåä ÿâëÿþòñÿ ãðàíÿìè ýòîãî ïàðàëëåëåïèïåäà, ñòîðîíû ýòèõ ïàðàëëåëîãðàììîâ ÿâëÿþòñÿ ðåáðàìè ïàðàëëåëåïèïåäà, à âåðøèíû ïàðàëëåëîãðàììîâ — âåðøèíàìè ïàðàëëåëåïèïåäà. Ó ïàðàëëåëåïèïåäà êàæäàÿ ãðàíü ÿâëÿåòñÿ ïàðàëëåëîãðàììîì.
Êàê ïðàâèëî âûäåëÿþò ëþáûå 2-å ïðîòèâîëåæàùèå ãðàíè è íàçûâàþò èõ îñíîâàíèÿìè ïàðàëëåëåïèïåäà, à îñòàâøèåñÿ ãðàíè — áîêîâûìè ãðàíÿìè ïàðàëëåëåïèïåäà. Ðåáðà ïàðàëëåëåïèïåäà, êîòîðûå íå ïðèíàäëåæàò îñíîâàíèÿì ÿâëÿþòñÿ áîêîâûìè ðåáðàìè.
2 ãðàíè ïàðàëëåëåïèïåäà, êîòîðûå èìåþò îáùåå ðåáðî ÿâëÿþòñÿ ñìåæíûìè, à òå, êîòîðûå íå èìåþò îáùèõ ðåáåð — ïðîòèâîïîëîæíûìè.
Îòðåçîê, êîòîðûé ñîåäèíÿåò 2 âåðøèíû, êîòîðûå íå ïðèíàäëåæàò 1-îé ãðàíè ÿâëÿåòñÿ äèàãîíàëüþ ïàðàëëåëåïèïåäà.
Äëèíû ðåáåð ïðÿìîóãîëüíîãî ïàðàëëåëåïèïåäà, êîòîðûå íå ïàðàëëåëüíû, ÿâëÿþòñÿ ëèíåéíûìè ðàçìåðàìè (èçìåðåíèÿìè) ïàðàëëåëåïèïåäà. Ó ïðÿìîóãîëüíîãî ïàðàëëåëåïèïåäà 3 ëèíåéíûõ ðàçìåðà.
Òèïû ïàðàëëåëåïèïåäà.
Ñóùåñòâóåò íåñêîëüêî âèäîâ ïàðàëëåëåïèïåäîâ:
Ïðÿìûì ÿâëÿåòñÿ ïàðàëëåëåïèïåä ñ ðåáðîì, ïåðïåíäèêóëÿðíûì ïëîñêîñòè îñíîâàíèÿ.
Ïðÿìîé ïàðàëëåëåïèïåä ñ ïðÿìîóãîëüíèêîì â îñíîâàíèè ÿâëÿåòñÿ ïðÿìîóãîëüíûì ïàðàëëåëåïèïåäîì. Ó ïðÿìîóãîëüíîãî ïàðàëëåëåïèïåäà êàæäàÿ èç ãðàíåé ÿâëÿåòñÿ ïðÿìîóãîëüíèêîì.

Íàêëîííûé ïàðàëëåëåïèïåä — ýòî ïàðàëëåëåïèïåä, ó êîòîðîãî áîêîâûå ãðàíè ðàñïîëîæåíû, ïî îòíîøåíèþ ê îñíîâàíèÿì, ïîä óãëîì, íå ðàâíûì 90 ãðàäóñîâ.

Ïðÿìîóãîëüíûé ïàðàëëåëåïèïåä, ó êîòîðîãî âñå 3 èçìåðåíèÿ èìåþò ðàâíóþ âåëè÷èíó, ÿâëÿåòñÿ êóáîì. Êàæäàÿ èç ãðàíåé êóáà – ýòî ðàâíûå êâàäðàòû.
Ïðîèçâîëüíûé ïàðàëëåëåïèïåä. Îáú¸ì è ñîîòíîøåíèÿ â íàêëîííîì ïàðàëëåëåïèïåäå â îñíîâíîì îïðåäåëÿþòñÿ ïðè ïîìîùè âåêòîðíîé àëãåáðû. Îáú¸ì ïàðàëëåëåïèïåäà ðàâíÿåòñÿ àáñîëþòíîé âåëè÷èíå ñìåøàííîãî ïðîèçâåäåíèÿ 3-õ âåêòîðîâ, êîòîðûå îïðåäåëÿþòñÿ 3-ìÿ ñòîðîíàìè ïàðàëëåëåïèïåäà (êîòîðûå èñõîäÿò èç îäíîé âåðøèíû). Ñîîòíîøåíèå ìåæäó äëèíàìè ñòîðîí ïàðàëëåëåïèïåäà è óãëàìè ìåæäó íèìè ïîêàçûâàåò óòâåðæäåíèå, ÷òî îïðåäåëèòåëü Ãðàìà äàííûõ 3-õ âåêòîðîâ ðàâíÿåòñÿ êâàäðàòó èõ ñìåøàííîãî ïðîèçâåäåíèÿ.
Ñâîéñòâà ïàðàëëåëåïèïåäà.
- Ïàðàëëåëåïèïåä ñèììåòðè÷åí îòíîñèòåëüíî ñåðåäèíû åãî äèàãîíàëè.
- Âñÿêèé îòðåçîê ñ êîíöàìè, êîòîðûå ïðèíàäëåæàò ïîâåðõíîñòè ïàðàëëåëåïèïåäà è êîòîðûé ïðîõîäèò ÷åðåç ñåðåäèíó åãî äèàãîíàëè, äåëèòñÿ åþ íà äâå ðàâíûå ÷àñòè. Âñå äèàãîíàëè ïàðàëëåëåïèïåäà ïåðåñåêàþòñÿ â 1-îé òî÷êå è äåëÿòñÿ åþ íà äâå ðàâíûå ÷àñòè.
- Ïðîòèâîïîëîæíûå ãðàíè ïàðàëëåëåïèïåäà ïàðàëëåëüíû è èìåþò ðàâíûå ðàçìåðû.
- Êâàäðàò äëèíû äèàãîíàëè ïðÿìîóãîëüíîãî ïàðàëëåëåïèïåäà ðàâíÿåòñÿ ñóììå êâàäðàòîâ 3-õ åãî èçìåðåíèé.
 ïàðàëëåëåïèïåä âïèñûâàþò òåòðàýäð. Îáúåì ýòîãî òåòðàýäðà áóäåò ðàâíÿòüñÿ òðåòüåé ÷àñòè îáúåìà ïàðàëëåëåïèïåäà.


Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
| Ïîìîùü â ðåøåíèè çàäà÷ ïî ãåîìåòðèè, ó÷åáíèê îíëàéí (âñå êàëüêóëÿòîðû ïî ãåîìåòðèè). | |
| Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
Ãåîìåòðè÷åñêèå ôèãóðû. | |
| Ãåîìåòðè÷åñêèå ôèãóðû – ïèðàìèäà, ïðÿìîóãîëüíèê, ðîìá, óãëû, øàð, ïàðàëëåëîãðàìì, ïàðàëëåëåïèïåä, ïðèçìà, ñâîéñòâà, ôîðìóëû ãåîìåòðè÷åñêèõ ôèãóð | |
| Ãåîìåòðè÷åñêèå ôèãóðû. | |
Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ãåîìåòðèè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ãåîìåòðè÷åñêèå ôèãóðû. Ïðèçìà. Îáúåì ïðèçìû. | |
| Ïðèçìà ìíîãîãðàííèê, 2 ãðàíè ýòî êîíãðóýíòíûå (ðàâíûå) ìíîãîóãîëüíèêè, êîòîðûå ëåæàò â ïàðàëëåëüíûõ ïëîñêîñòÿõ, à îñòàâøèåñÿ ãðàíè ïàðàëëåëîãðàììû, èìåþùèå îáùèå ñòîðîíû ñ ýòèìè ìíîãîóãîëüíèêàìè. | |
| Ãåîìåòðè÷åñêèå ôèãóðû. Ïðèçìà. Îáúåì ïðèçìû. | |
Источник
