Какое утверждение содержится во втором законе ньютона
Законы Ньютона – это три кита, на которых держатся вся современная механика. Мы уже подробно рассматривали первый закон Ньютона в этой статье и делали обобщенный материал по всем законам Ньютона . Этот материал является логическим продолжением предыдущих статей.
Я заметил, что основные сложности в понимании возникают часто из-за неумения вникать в формулировки. Поэтому, все мои статьи на эту тему содержат развернутые пояснения и примеры из реальной жизни. Я очень надеюсь, что такая логика изложения сделает чтение интересным, а результат освоения будет отличным.
Многие читатели отмечают, что законы Ньютона как оно говорится – притянуты за уши. Друзья и коллеги учёные! Я, в некотором смысле, готов согласиться с вашими мыслями и фактов достаточно. Но, во-первых, мы говорим про модель, имеющую набор неопровержимых фактов. А во-вторых, моя задача упростить обучение физике по школьной программе.
Итак, что-то мы отступили от основной темы.
Второй закон Ньютона по моему опыту работы с учениками воспринимается легче всего. И действительно, когда нет каких-то абстрактных понятий, типа инерции (правда и она там присутствует, но за “кадром” определения) или противодействий, запомнить всё намного проще, так как можно перенести всё на реальную жизнь и представить.
Формулировка второго закона Ньютона
Сам Исаак Ньютон сформулировал второй закон таким образом:
Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
Согласитесь, звучит немного ужасающе. Куда понятнее выглядит осовремененная формулировка:
В инерциальных системах отсчёта ускорение (а), приобретаемое материальной точкой, прямо пропорционально вызывающей его силе (понятнее записать – векторной сумме сил, F), совпадает с ней по направлению и обратно пропорционально массе материальной точки (m). Или, если записать это аналитически, то:
Поэтапный разбор второго закона
Второй закон имеет не так много хитрых слов.
Инерциальные системы отсчёта…Что это такое? Мы уже рассказывали вам об этом в статье про первый закон. Не будем долго на это задерживаться. Если коротко, то это такие системы отсчёта, где существует инерция (читай как все для наших условий).
Материальная точка – наверняка вы уже сталкивались в физике с этим понятием. Что такое материальная точка и почему внимание акцентируется именно на ней? Всё просто, если представить тот же камень, который вы бросили в кота не как материальную точку, то нужно будет учитывать множество дополнительных параметров при расчёте. Камень не симметричный, имеет неравномерное распределение массы, может развалиться при полёте. Всё это не даёт сконцентрировать внимание на основной закономерности. В итоге мы говорим о простейшей модели, которая является материальной точкой, а размерами, формой, вращением и внутренней структурой можно пренебречь в условиях исследуемой задачи.
Дальше речь идёт про силы. Иногда оно формулируется как векторная сумма сил или равнодействующая.
Гораздо понятнее использовать именно формулировку “векторная сумма”. Про вектора у нас был целый обучающий ролик, советую изучить:
Но для тех, кто спешит, отметим здесь – векторная сумма есть такая сумма, которая учитывает направление вектора и его позиционирование в пространстве.
Ну и если вы вдруг забыли, что такое сила, то физика понимает силу, какфизическую векторную величину (т.е. направленную), являющуюся мерой воздействия на данное тело со стороны других тел (или полей). Определение такое себе, как это модно сейчас говорить. Но лучше и не скажешь.
Осталось одно ключевое понятие.
Это ускорение.
Что такое ускорение? Всё очень просто. Ускорение есть мера изменения скорости тела. Если мы бежим со скоростью 8 км/ч и эта скорость у нас одинакова как в первый час, так и во второй, то мы бежим равномерно. Если мы бежим первый час на 8 км/ч, а второй час на 12 км/ч (что, поверьте, маловероятно), то мы имеем некоторое ускорение.
Ну и уточняется, что направлено это ускорение также, как и равнодействующая всех сил.
Про массу говорить не будем, уж извините 🙂 А то изыскания выйдут далеко за школьную программу и мы будем пытаться понять, что же такое масса на самом деле и почему она есть.
Теперь сформулируем второй закон Ньютона, как сапожники (простите, господа сапожники, среди вас много кандидатов наук…))
Равнодействующая сил (т.е. векторная сумма сил), действующих на тело, равна произведению массы этого тела на его ускорение.
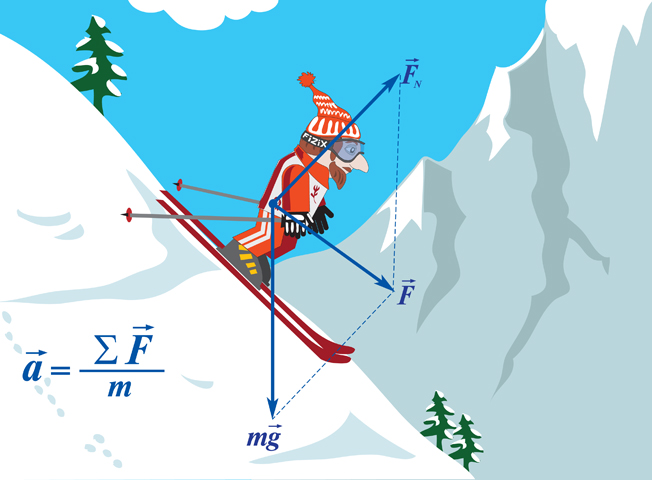
Теперь взглянем на чертеж ниже и всё вдруг станет понятным.
Скажем, взглянем на тело с массой m1.
Записываем для него второй закон Ньютона.
Какая тут векторная сумма всех сил?
Она складывается из силы натяжения нити (Fн), силы трения (Fтр), силы реакции опоры Т (Это то ,с какой силой деревяшка пружинит) и силы тяжести. Всё это равно произведению массы тела m1 на его ускорение. Почему всё векторное? Да потому, что направление тут очень важно! Так, сила реакции опоры имеет направление и ориентировано определенным образом относительно плоскости. И т.д. и т.п.
Надеюсь, всем всё было понятно! Если вопросы остались, то обязательно задавайте их нам, например на стене в группе https://vk.com/inznan
Смотрите инженерные знания! Подписывайтесь на канал и всем удачи.
————————————————
Полезно будет прочитать:
Источник
Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».
Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.
(Эпиграмма 18-го века)
Но сатана недолго ждал реванша –
Пришел Эйнштейн, и стало все как раньше.
(Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих “Математических началах натуральной философии”.
Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.

Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
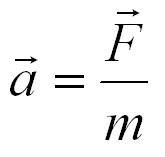

Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.
Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
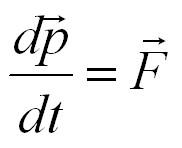
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
Третий закон Ньютона
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
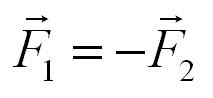
Другими словами, третий закон Ньютона – это закон действия и противодействия.

Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
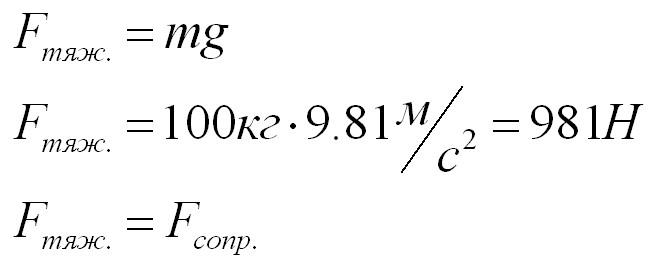
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
- Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
- Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
- Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
- Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
- Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.
Дорогие друзья, помните – любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы. Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!
В самом конце предлагаем посмотреть видеоурок на тему “Законы Ньютона”.
Источник
Продолжение. Начало в О чем спорят физики ? Виды механик и их пространства. Предыдущая статья: Пространство классической механики.
В основе классической механики Ньютона лежат три закона Ньютона. Впервые законы механики было сформулированы еще Ньютоном в 1687 г. в его «Математических началах натуральной философии».
Законы Ньютона считались абсолютно точными вплоть до начала 20 века, когда на смену им пришла специальная теория относительности (СТО). Все современные знания о механике в той или иной мере опираются на законы Ньютона и Кеплера, лишь дополняя и уточняя их. Ньютоновская механика перестает давать точные результаты, когда речь идет о скоростях, близких к скорости света, а также микроскопических объектах, с размерами порядка размера атомов и менее. Также есть и мнение, что и для очень больших и очень маленьких масс, а также на очень больших, космических, а также на очень маленьких расстояниях законы Ньютона работают с ошибками. Но это – всего лишь мнения. Реальность, скорее всего, говорит об обратном.
Несмотря на то, что законы Ньютона определены для ИСО в евклидовом пространстве, они остаются справедливыми и в произвольной с.к. в ковариантном тензорном виде. Главное: законы Ньютона формулируются в независимых абсолютных пространстве и времени.
Хочу отметить, что три закона Ньютона определены в аффинном пространстве. Это пространство, в котором определены только точки, прямые и плоскости в объединяющем их трехмерном пространстве. Без расстояний. Об этом обычно нигде не говорится. Но совместно с принципом изотропности пространства пространство КМН становится евклидовым.
Конкретные законы взаимодействия не являются законами Ньютона, но описываются ими.
Первый закон Ньютона. Инерция и инерциальные с.о.
Первый закон Ньютона говорит, что существуют инерциальные системы отсчета. Сейчас это кажется очевидным, но во времена Аристотеля, например, считалось, что для всякого движения должна существовать сила. Инерциальные системы отсчета – это системы отсчета, не испытывающие ускорения. В таких системах справедлив закон инерции: любое тело, на которое не действуют внешние силы или действие этих сил компенсируется, находится в состоянии покоя или равномерного прямолинейного движения. Следствием этого закона является евклидовость пространства и галилеевость пространства-времени. Точнее, аффинность Пространства-времени. Всякая система отсчета, движущаяся относительно инерциальной равномерно и прямолинейно, является инерциальной.
Фактически первый закон Ньютона говорит, что нет разницы между покоем тела и равномерным прямолинейным движением: это просто разные состояния относительного движения.
Понаблюдаем за поведением различных тел относительно Земли, выбрав неподвижную систему отсчета, связанную с поверхностью Земли, в различных динамических ситуациях. Мы обнаружим, что скорость любого тела изменяется только под действием других тел. Например, пусть тело стоит на неподвижной тележке. Толкнем тележку – и тело опрокинется против движения. Если же, наоборот, резко остановить двигающуюся тележку с телом, оно опрокинется по направлению движения. Или, при пренебрежимо малом трении, шайба, движущаяся по ледяной поверхности катка, движется почти без изменения скорости, пока не достигнет края катка. В первом случае, если бы трение между тележкой и телом отсутствовало, то тело не опрокинулось бы. Произошло бы следующее: так как скорость стоящего тела равна нулю, а скорость тележки стала увеличиваться, тележка выскользнула бы из-под неподвижного тела вперед. Во втором случае при торможении тележки стоящее на ней тело сохранило бы свою скорость движения и соскользнуло вперед с остановившейся тележки.
В рассмотренном случае видно, что тело стремится сохранить свое первоначальное состояние движения: покоящееся тело стремится сохранить свое состояние покоя, движущееся – состояние движения. О том, что телу свойственно сохранять не любое движение, а именно прямолинейное, свидетельствует, например, следующий опыт. Шарик, двигавшийся прямолинейно по плоской горизонтальной поверхности, сталкиваясь с преградой, имеющей криволинейную форму, под действием этой преграды вынужден двигаться по дуге. Однако когда шарик доходит до края преграды, он перестает двигаться криволинейно и вновь начинает двигаться по прямой. Обобщая результаты упомянутых (и аналогичных им) наблюдений, можно сделать вывод, что если на данное тело не действуют другие тела или их действия взаимно компенсируются, это тело покоится или же скорость его движения остается неизменной относительно системы отсчета, неподвижно связанной с поверхностью Земли.
Явление сохранения телом состояния покоя или прямолинейного равномерного движения при отсутствии или компенсации внешних воздействий на это тело называют движением по инерции.
Во времена Аристотеля (в 4 в.д.н.э.) вышеприведенные объяснения примеров считались бы ошибочными. Аристотель считал, что естественным положением тела является покой, – конечно, по отношению к Земле. В этом утверждении отрицается существование ИСО и утверждается существование выделенной системы отсчета – поверхности земли – и даже более – конкретных ее участков. Всякое же перемещение тела по отношению к Земле должно было иметь причину – силу. Если же причины двигаться нет, то тело должно останавливаться, перейти в своё естественное состояние покоя.
К выводу о существовании явления инерции впервые пришел Галилей (1564—1642), а затем Ньютон. С понятием инерции в классической механике связано определение «инерциальной с.о.» или ИСО. Галилей установил, что никакими механическими опытами, поставленными внутри инерциальной системы отсчета, невозможно установить, покоится эта система или движется равномерно и прямолинейно. Это утверждение носит название принципа относительности Галилея или механического принципа относительности. Следствием его является аффинная геометрия пространства и времени и ГПТК. Этот принцип был впоследствии развит А.Эйнштейном и является одним из постулатов специальной теории относительности (СТО). Частный случай такого пространства – евклидово (евклидово), для СТО – пространство Минковского.
Использован рисунок с адреса: https://avatars.mds.yandex.net/get-pdb/2377820/57904ee0-fe86-41e0-b7e5-2ff2ec9ff739/s1200?webp=false (найден по ЯндексПоиску).
Второй закон Ньютона. Масса м.т. Сила, импульс м.т.
В результате многочисленных опытов было замечено, что три параметра – масса, сила и ускорение – тесно связаны между собой. Но прежде чем получить этот закон, необходимо было научиться измерять эти параметры, создать эталоны и измерительные приборы на их основе.
Второй закон Ньютона описывает взаимосвязь между приложенной к материальной точке силой и её ускорением. Этот закон, по сути, вводит понятие силы – как меры воздействия на тело с целью изменения ее состояния движения, и массы – как меры податливости действию этой силы.
Под воздействием внешней силы материальной точке (далее – м.т.) получает ускорение и изменяет свою скорость. Причем разные м.т. под воздействием одной и той же силы получают разные ускорения. Причем было замечено, что это ускорение обратно пропорционально количеству вещества в м.о. Параметр “количество вещества” м.т., от которого зависит ускорение м.т. под воздействием приложенной силы, называется массой м.т. В классической механике законы движения м.т. формулируются через второй закон Ньютона:
F = ma.
Это уравнение называется уравнением движения м.т. Здесь F – сила, приложенная к м.т., m – масса м.т., a – ускорение м.т.
Второй закон Ньютона не является кинематическим уравнением, потому что в правой части стоит выражение, определяющее причину появления ускорения м.о. В данном случае это сила F. Это уравнение динамики. Кстати, первый закон Ньютона также является законом динамики, несмотря на то, что причины покоя – силы – как таковой там нет, но есть причина покоя – отсутствие этой самой силы.
Третий закон Ньютона
Первый закон Ньютона относится к глобальным свойствам пространства – существованию ИСО, и движению свободного тела в ней, второй закон Ньютона относится к закону движения одного тела под действием силы, неважно какой, в частности – силы инерции. Третий закон Ньютона.
Третий закон Ньютона объясняет, что происходит с взаимодействующими телами и относится не к одному телу, а к м.о. или системе м.т. (далее – с.м.т.), точнее – к их взаимодействию. Во всех случаях, когда на какое-либо тело действует сила, имеет место не одностороннее действие, а взаимодействие тел. Силы такого взаимодействия между телами имеют одинаковую природу, появляются и исчезают одновременно, по крайней мере – в классической механике. Опыты показывают, что при взаимодействии двух тел оба тела получают ускорения, направленные по одной прямой в противоположные стороны.
В общем случае третий закон справедлив для непосредственно контактирующих м.о. Но действие третьего закона Ньютона не заканчивается на непосредственно контактно взаимодействующих м.о. В галилеевом пространстве при взаимодействии с помощью полей, действующих на другие тела моментально (например, гравитационное), также работает этот закон.
Суть третьего закона Ньютона для замкнутой системы взаимодействующих м.т. в инерциальной с.о. заключается в следующих утверждениях:
1. Сила взаимодействия между двумя разнесенными в пространстве м.т. направлена по прямой, соединяющей эти м.т. Этот принцип является следствием изотропности взаимодействия относительно вращений вокруг прямой, соединяющей две точки, а также зеркальной симметрии относительно этой же прямой или плоскости, проходящей через нее.
2. Любые две м.т. 1 и 2 действуют друг на друга с одинаковой, но противоположно направленной силой:
F₁₂ = – F₂₁.
3. В с.м.т. любые две м.т. взаимодействуют независимо от наличия или отсутствия других м.т. (принцип независимости и аддитивности взаимодействия м.т.):
F ᵤ = S ᵥ F ᵤ ᵥ,
где F ᵤ – сила, действующая на u–ю частицу (м.т.) системы,
F ᵤ ᵥ – сила, действующая на u–ю м.т. системы со стороны v–й частицы системы,
S ᵥ – знак суммирования по всем взаимодействующим объектам.
Таким образом, для замкнутой локальной (консервативной) системы взаимодействующих объектов:
SFᵤ ᵥ = 0.
4. При контактном взаимодействии двух м.о. 1 и 2 силы противодействия (без трения) приложены к точкам их контакта v, равны по величине и направлены противоположно и перпендикулярно к плоскости касания м.о.:
F ᵥ ₁₂ = – F ᵥ ₂₁.
При наличии трения к этим нормальным силам прибавляются касательные к линии соприкосновения силы трения Fᵤ , приложенные в точке касания
F ᵤ ₁₂ = – F ᵤ ₂₁.
Плоскость касания должна быть хотя бы у одной из взаимодействующих тел. В противном случае для определения направления действующих сил необходимы дополнительные данные.
Эта формулы выражают факт равенства действия и противодействия для всех взаимодействующих объектов евклидова (галилеева, ньютонова) пространства.
Наиболее простой и емкой формулировкой третьего закона Ньютона является следующая: действие равно противодействию.
Примером, подтверждающим этот закон, является соударение двух одинаковых бильярдных шаров. Обратите внимание на следующий опыт. Поставьте на стол два бильярдных шара, возьмите кий и ударьте им по одному из шаров точно по линии, их соединяющей. Вы увидите, что ударивший шар остановится, а шар, по которой ударили, начнет двигаться с той же скоростью
Законы Ньютона являются основными законами механики. Из них могут быть выведены все остальные законы механики. Как видно из вышеизложенного, законы Ньютона исключительно просты в своей математической интерпретации.
Если хотите узнать, что обозначает слово или словосочетание, в ОПЕРЕ выделите это слово(сочетание), нажмите правую клавишу мыши и выберите “Искать в …”, далее – “Yandex”. Все! О-ля-ля!
Если вам понравилась статья, то поставьте “лайк” и подпишитесь на канал! Этим вы поможете каналу.
Ссылка на мою статью Как написать формулы в статье на Дзен?
Мои странички на Дзен: https://zen.yandex.ru/id/5e036c95fc69ab00aecfe6e9
Источник
