Какое свойство заряда отражает первый закон кирхгофа

С помощью первого и второго законов Кирхгофа, а также закона Ома можно найти параметры схемы любой сложности. Поэтому знание, а самое главное понимание этих трех законов строго обязательно для всех кто занимается электроникой. В этой статье я постараюсь максимально просто объяснить и на простейших схемах показать, как работают законы Кирхгофа. Итак, давайте начнем.
Первый закон Кирхгофа
Итак, Первый закон Кирхгофа говорит нам о том, что сумма токов в любом узле абсолютно любой электрической цепи равна нулю. Или так же говорит, что алгебраическая сумма втекающих токов равна алгебраической сумме вытекающих из узла токов.
Узлом в сети называется такой участок цепи, в котором соединяются три и более проводника. Ток, входящий в узел, обозначается стрелочкой, имеющей направление к узлу, а вытекающий – стрелочкой, имеющей направление от узла
И теперь на основании первого закона Кирхгофа запишем следующее уравнение:
Эта же формула может быть записана следующим образом:
При этом положительные и отрицательные знаки токам присвоены условно и если вы поменяете их с точностью до наоборот, то ничего принципиально не изменится.
Для того, чтобы наглядно увидеть работу Первого закона Кирхгофа, давайте соберем простейшую схему.
В качестве источника питания вы можете выбрать абсолютно любой элемент, начиная от пальчиковой батарейки и заканчивая блоком питания с возможностью регулировки.
Примечание. Не обязательно использовать резисторы с номиналом, который указан на схеме. Вы можете подобрать абсолютно любые, какие есть у вас в наличии.
Итак, согласно 1 закону Кирхгофа у нас должно быть верно, следующее уравнение:
Либо верно:
Для проведения практических измерений нам нужно в место на схеме где указан амперметр подключить, например, мультиметр.
Как мы видим по показаниям мультиметра закон работает.
Второй закон Кирхгофа
С пониманием второго закона у многих радиолюбителей в самом начале пути возникают трудности. Но если объяснить по-простому, то все более чем просто, сейчас докажу.
Итак, определение второго закона Кирхгофа звучит так:
В любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех пассивных элементах цепи.
Согласитесь, звучит не очень понятно, а вот если сказать проще то:
Сумма ЭДС в замкнутом контуре равна сумме падений напряжений и формула, выражающая этот закон, будет иметь такой вид
Или же
Для понимания давайте разберем самую простую схемку с одним пассивным элементом (резистором) и источником питания в виде пальчиковой батарейки.
Так как у нас резистор один, то падение напряжение на его выводах будет равно величине ЭДС элемента питания (батарейки), то есть 1,5 В = 1,5 В.
Если несколько усложнить схему и добавить к резистору еще один с аналогичным сопротивлением, то в этом случае, то напряжение в 1,5 Вольта поделится пополам на резисторах и будет равно 0,75 В.
Так же произойдет деление напряжения, если мы в цепочку включим третий резистор с одинаковым сопротивлением.
Формула обретет следующий вид:
Давайте для понимания соберем эту схему и произведем измерения.
Как видите, согласно второму закону Кирхгофа, небольшое расхождение в показаниях мультиметра спишем на погрешность прибора (китай как никак).
Кроме одного источника питания в цепи их может быть несколько как, например, в этой схеме
В этом случае у нас два источника питания подключены последовательно встречно, в таком варианте к нашим резисторам будет приложена разность ЭДС, то есть формула обретет следующий вид:
Второй закон Кирхгофа функционирует в цепях независимо от того сколько источников ЭДС и нагрузок будет в схеме. Так же нет принципиальной разницы, где они будут располагаться.
Так же первый и второй законы Кирхгофа одинаково применимы как для постоянного, так и для переменного тока.
Статья оказалась полезна или интересна, тогда ставим лайк и спасибо за уделенное внимание!
Источник
Закон Кирхгофа (правила Кирхгофа), сформулированные Густавом Кирхгофом в 1845 году, являются следствиями из фундаментальных законов сохранения заряда и безвихревости электростатического поля.
Закон Кирхгофа – это соотношения, выполняемые между токами и напряжениями на участках любых электрических цепей. Они позволяют рассчитывать любые электрические цепи: постоянного, переменного или квазистационарного тока.
При формулировании правил Кирхгофа используют такие понятия, как ветвь, контур и узел электрической цепи.
- Ветвь – участок электрической цепи с одни и тем же током.
- Узел – точка соединения трех или более ветвей.
- Контур – замкнутый путь, проходящий через несколько узлов и ветвей разветвлённой электрической цепи.
При обходе надо учесть, что ветвь и узел могут одновременно принадлежать нескольким контурам. Правила Кирхгофа справедливы как для линейных, так и для нелинейных цепей при любом характере изменения во времени токов и напряжений. Правила Кирхгофа широко применяются при решении задач электротехники за счет легкости в расчетах.
1 закон Кирхгофа
В цепях, состоящих из последовательно соединенных источника и приемника энергии, соотношения между током, сопротивлением и ЭДС всей цепи или на каком-либо участке цепи определяются законом Ома. Но на практике в цепях токи от какой-либо точки идут по разным путям (Рис. 1). Поэтому становиться актуальным введение новых правил для проведения расчетов электрических цепей.

Рис. 1. Схема параллельного соединения проводников.
Так, при параллельном соединении проводников начала всех проводников соединены в одну точку, а концы проводников – в другую точку. Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.
Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А, растекается далее по трем сопротивлениям и равен сумме токов, выходящих из этой точки: I = I1 + I2 + I3.
Согласно первому правилу Кирхгофа алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла – отрицательным.
Запишем первый закон Кирхгофа в комплексной форме:

Первый закон Кирхгофа гласит, что алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла. То есть, сколько тока втекает в узел, столько же вытекает (как следствие закона сохранения электрического заряда).
Алгебраическая сумма – это сумма, в которую входят слагаемые со знаком плюс и со знаком минус.

Рис. 2. i_1+i_4=i_2+i_3.
Рассмотрим применение 1 закона Кирхгофа на следующем примере:

- I1 – это полный ток, текущий к узлу А, а I2 и I3 — токи, вытекающие из узла А.
- Тогда мы можем записать: I1 = I2 + I3.
- Аналогично для узла B: I3 = I4 + I5.
- Пусть, что I4 = 5 А и I5 = 1 А, получим: I3 = 5 + 1 = 6 (А).
- Пусть I2 = 10 А, получим: I1 = I2 + I3 = 10 + 6 = 16 (А).
- Запишем подобное соотношение для узла C: I6 = I4 + I5 = 5 + 1 = 6 А.
- А для узла D: I1 = I2 + I6 = 10 + 6 = 16 А
- Таким образом мы наглядно видим справедливость первого закона Кирхгофа.
2 закон Кирхгофа
При расчете электрических цепей в большинстве случаев нам встречаются цепи, образующие замкнутые контуры. В состав таких контуров, кроме сопротивлений, могут входить ЭДС (источники напряжений). На рисунке 4 представлен участок такой электрической цепи. Произвольно выбираем положительные направления токов. Обходим контур от точки А в произвольном направлении (выберем по часовой стрелке). Рассмотрим участок АБ: происходит падение потенциала (ток идет от точки с высшим потенциалом к точке с низшим потенциалом).

- На участке АБ: φА + E1 – I1r1 = φБ.
- БВ: φБ – E2 – I2r2 = φВ.
- ВГ: φВ – I3r3 + E3 = φГ.
- ГА: φГ – I4r4 = φА.
- Складывая данные уравнения, получим: φА + E1 – I1r1 + φБ – E2 – I2r2 + φВ – I3r3 + E3 + φГ – I4r4 = φБ + φВ + φГ + φА
- или: E1 – I1r1 – E2 – I2r2 – I3r3 + E3 – I4r4 = 0.
- Откуда имеем следующее: E1 – E2 + E3 = I1r1 + I2 r2 + I3r3 + I4r4.
Таким образом, получаем формулу второго закона Кирхгофа в комплексной форме:
Уравнение для постоянных напряжений – 
Уравнение для переменных напряжени – 
Теперь можем сформулировать определение 2 (второго) закона Кирхгофа:
Второй закон Кирхгофа гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура, равна алгебраической сумме ЭДС, входящих в этот контур. В случае отсутствия источников ЭДС, суммарное напряжение равно нулю.

Иначе формулируя второе правило Кирхгофа, можно сказать: при полном обходе контура потенциал, изменяясь, возвращается к начальному значению.
При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура, при этом падение напряжения на ветви считается положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, в противном случае – отрицательным.
Определить знак можно по алгоритму:
- 1. выбираем направление обхода контура (по или против часовой стрелки);
- 2. произвольно выбираем направления токов через элементы цепи;
- 3. расставляем знаки для напряжений и ЭДС по правилам (ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура со знаком «+», иначе – «-»; напряжения, падающие на элементах цепи, если ток, протекающий через эти элементы совпадает по направлению с обходом контура, со знаком «+», в противном случае – «-»).
Закон Ома является частным случаем второго правила для цепи.
Приведем пример применения второго правила Кирхгофа:

По данной электрической цепи (Рис 6) необходимо найти ее ток. Произвольно берем положительное направление тока. Выберем направление обхода по часовой стрелке, запишем уравнение 2 закона Кирхгофа:

Знак минус означает, что выбранное нами направление тока противоположно его действительному направлению.
Решение задач
1. По приведенной схеме записать законы Кирхгофа для цепи.

| Дано: | Решение: |
|---|---|
|
|
2. На рисунке приведена цепь с двумя источниками ЭДС величиной 12 В и 5 В, с внутренним сопротивлением источников 0,1 Ом, работающих на общую нагрузку 2 ома. Как будут распределены токи в этой цепи, какие они имеют значения?.

Источник
При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие полностью определить режим её работы.
Воспользуйтесь программой онлайн-расчёта электрических цепей.
Прежде чем перейти к самим законам Кирхгофа, дадим определение ветвей и узлов электрической цепи.
Ветвью электрической цепи называется такой её участок, который состоит только из последовательно включённых источников ЭДС и сопротивлений, вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трёх и более ветвей. При обходе по соединённым в узлах ветвям можно получить замкнутый контур электрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза [1].
Первый закон Кирхгофа
Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:
∑i = 0,
или в комплексной форме
∑I = 0.
Второй закон Кирхгофа
Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС:
∑Z ∙ I = ∑E.
Количество уравнений, составляемых для электрической цепи по первому закону Кирхгофа, равно Nу – 1, где Nу – число узлов. Количество уравнений, составляемой для электрической цепи по второму закону Кирхгофа, равно Nв – Nу + 1, где Nв – число ветвей. Количество составляемых уравнений по второму закону Кирхгофа легко определить по виду схемы: для этого достаточно посчитать число «окошек» схемы, но с одним уточнением: следует помнить, что контур с источником тока не рассматривается.
Опишем методику составления уравнений по законам Кирхгофа. Рассмотрим её на примере электрической цепи, представленной на рис. 1.
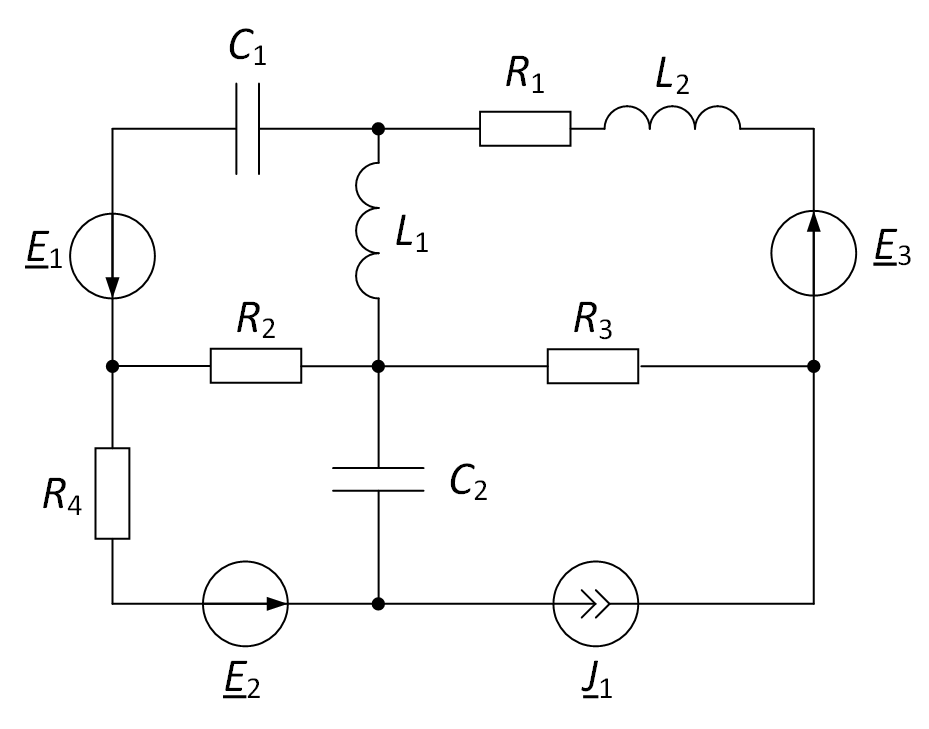
Рис. 1. Рассматриваемая электрическая цепь
Для начала необходимо задать произвольно направления токов в ветвях и задать направления обхода контуров (рис. 2).
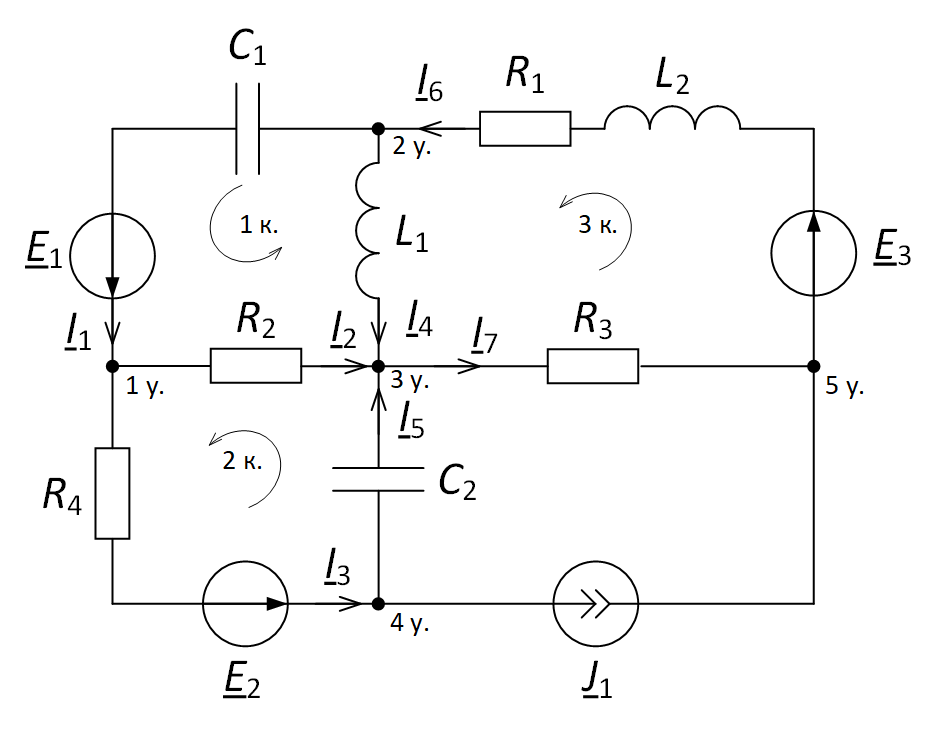
Рис. 2. Задание направления токов и направления обхода контуров для электрической цепи
Количество уравнений, составляемых по первому закону Кирхгофа, в данном случае равно 5 – 1 = 4. Количество уравнений, составляемых по второму закону Кирхгофа, равно 3, хотя «окошек» в данном случае 4. Но напомним, что «окошко», содержащее источник тока J1, не рассматривается.
Составим уравнения по первому закону Кирхгофа. Для этого «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» — со знаком «-». Отсюда для узла «1 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:
I1 – I2 – I3 = 0;
для узла «2 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:
—I1 – I4 + I6 = 0;
для узла «3 у.»:
I2 + I4 + I5 – I7 = 0;
для узла «4 у.»:
I3 – I5 – J1 = 0
Уравнение для узла «5 у.» можно не составлять.
Составим уравнения по второму закону Кирхгофа. В этих уравнениях положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Для контура «1 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:
ZC1 ∙ I1 + R2 ∙ I2 – ZL1 ∙ I4 = E1;
для контура «2 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:
-R2 ∙ I2 + R4 ∙ I3 + ZC2 ∙ I5 = E2;
для контура «3 к.»:
ZL1 ∙ I4 + (ZL2 + R1) ∙ I6 + R3 ∙ I7 = E3,
где ZC = — 1/(ωC), ZL = ωL.
Таким образом, для того, чтобы найти искомые токи, необходимо решить следующую систему уравнений:
В данном случае это система из 7 уравнений с 7 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:
Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:
>> syms R1 R2 R3 R4 Zc1 Zc2 Zl1 Zl2 J1 E1 E2 E3;
>> A = [1 -1 -1 0 0 0 0;
-1 0 0 -1 0 1 0;
0 1 0 1 1 0 -1;
0 0 1 0 -1 0 0;
Zc1 R2 0 -Zl1 0 0 0;
0 -R2 R4 0 Zc2 0 0;
0 0 0 Zl1 0 (R1+Zl2) R3];
>> b = [0;
0;
0;
J1;
E1;
E2;
E3];
>> I = Ab
В результате получим вектор-столбец I токов из семи элементов, состоящий из искомых токов, записанный в общем виде. Видим, что программный комплекс Matlab позволяет существенно упростить решение сложных систем уравнений, составленных по законам Кирхгофа.
Список использованной литературы
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
Источник
В сложных электрических цепях, то есть где имеется несколько разнообразных ответвлений и несколько источников ЭДС имеет место и сложное распределение токов. Однако при известных величинах всех ЭДС и сопротивлений резистивных элементов в цепи мы можем вычистить значения этих токов и их направление в любом контуре цепи с помощью первого и второго закона Кирхгофа. Суть законов Кирхгофа я довольно кратко изложил в своем учебнике по электронике, на страницах сайта https://www.sxemotehnika.ru.
Пример сложной электрической цепи вы можете посмотреть на рисунке 1.

Рисунок 1. Сложная электрическая цепь.
Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.
Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.
Первый закон Кирхгофа
Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.
Поясню первый закон Кирхгофа на примере рисунка 2.

Рисунок 2. Узел электрической цепи.
Здесь ток I1– ток, втекающий в узел , а токи I2 и I3 — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:
I1 = I2 + I3 (1)
Что бы подтвердить справедливость формулировки №2, перенесем токи I2 и I3 в левую часть выражения (1), тем самым получим:
I1 – I2 – I3 = 0 (2)
Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.
Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).
Можно посмотреть отдельный видеоурок по первому закону Кирхофа в разделе ВИДЕОУРОКИ.
Второй закон Кирхгофа.
Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.
Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:
1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).
2. Произвольно выбираем направление токов через элементы цепи.
3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:
– ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».
– напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».
Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.

Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.
E1- Е2 = -UR1 – UR2 или E1 = Е2 – UR1 – UR2 (3)
Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).
Расчеты электрических цепей с помощью законов Кирхгофа.
Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.
Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E1=12 в и E2=5 в , с внутренним сопротивлением источников r1=r2=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.

Рисунок 4. Пример расчета сложной электрической цепи.
Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:
I = I1 + I2,
так как I1 и I2 втекают в узел А, а ток I вытекает из него.
Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.
Для внешнего контура:
E1-E2 = Ur1 – Ur2 или E1-E2 = I1*r1 – I2*r2
Для внутреннего левого контура:
E1 = Ur1 + UR или E1 = I1*r1 + I*R
Итак, у нас получилась система их трех уравнений с тремя неизвестными:
I = I1 + I2;
E1-E2 = I1*r1 – I2*r2;
E1 = I1*r1 + I*R.
Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:
I = I1 + I2;
7 = 0,1I1 – 0,1I2;
12 = 0,1I1 +2I.
Далее из первого и второго уравнения выразим ток I2
I2=I – I1;
I2 = I1 – 70;
12 = 0,1I1 + 2I.
Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:
I – I1= I1 – 70;
12 = 0,1I1 + 2I.
Выражаем из первого уравнения значение I
I = 2I1– 70;
И подставляем его значение во второе уравнение
12 = 0,1I1 + 2(2I1 – 70).
Решаем полученное уравнение
12 = 0,1I1 + 4I1 – 140.
12 + 140= 4,1I1
I1=152/4,1
I1=37,073 (А)
Теперь в выражение I = 2I1– 70 подставим значение
I1=37,073 (А) и получим:
I = 2*37,073 – 70 = 4,146 А
Ну, а согласно первому закона Кирхгофа ток I2=I – I1
I2=4,146 – 37,073 = -32,927
Знак «минус» для тока I2 означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I2 вытекает из узла А.
Теперь полученные данные можно проверить на практике или смоделировать данную схему например в программе Multisim.
Скриншот моделирования схемы для проверки законов Кирхгофа вы можете посмотреть на рисунке 5.
 Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.
Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.
Для закрепления результатата предлагаю посмотреть подготовленное мной видео:
Источник



