Какое свойство точек серединного перпендикуляра к отрезку есть

Главная
Справочники
Справочник по геометрии 7-9 класс
Окружность
Свойства серединного перпендикуляра к отрезку

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

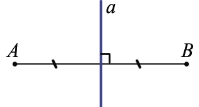
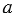Какое свойство точек серединного перпендикуляра к отрезку есть

Какое свойство точек серединного перпендикуляра к отрезку есть – серединный перпендикуляр к отрезку АВ.

Теорема

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.

Доказательство

1) Дано: m – серединный перпендикуляр отрезка АВ, О – середина АВ, М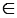 Какое свойство точек серединного перпендикуляра к отрезку есть m

Доказать: АМ = ВМ

Доказательство:

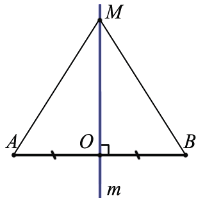
Какое свойство точек серединного перпендикуляра к отрезку есть

Если О = М, то АМ = ВМ, т.к. О – середина АВ.

Пусть О 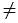Какое свойство точек серединного перпендикуляра к отрезку есть М. Рассмотрим ОАМ и ОВМ: так как m – серединный перпендикуляр отрезка АВ, то рассматриваемые треугольники прямоугольные. ОА = ОВ, т.к. О – середина отрезка АВ, ОМ – общий катет, следовательно, Какое свойство точек серединного перпендикуляра к отрезку есть ОАМ = ОВМ, по двум катетам, а в равных треугольниках против соответственно равных углов лежат равные стороны, поэтому АМ = ВМ.

2) Дано: m – серединный перпендикуляр отрезка АВ, О – середина АВ, АN = ВN

Доказать:N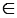 Какое свойство точек серединного перпендикуляра к отрезку есть m

Доказательство:

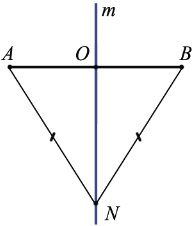
Какое свойство точек серединного перпендикуляра к отрезку есть

Рассмотрим произвольную точку N.

Если N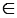 Какое свойство точек серединного перпендикуляра к отрезку есть АВ, то N = О, а, значит, она лежит на прямой m.

Если N не лежит на АВ, то Какое свойство точек серединного перпендикуляра к отрезку есть ANB – равнобедренный, так как АN = ВN. О – середина АВ, следовательно, NО – медиана ANB, а, значит, и высота по свойству равнобедренного треугольника. Поэтому NО Какое свойство точек серединного перпендикуляра к отрезку есть АВ, следовательно, прямые NО и m совпадают, так как по устовию m – серединный перпендикуляр отрезка АВ, т.е. N – точка прямой m. Теорема доказана.

Следствие 1

Следствие2

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Взаимное расположение прямой и окружности

Касательная к окружности

Градусная мера дуги окружности

Теорема о вписанном угле

Свойство биссектрисы угла

Теорема о пересечении высот треугольника

Вписанная окружность

Описанная окружность

Окружность

Правило встречается в следующих упражнениях:

7 класс

Задание 686,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 19,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 20,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 25,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 720,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 727,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1003,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1155,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1173,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1241,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Доказательство. Обозначим буквой M произвольную точку серединного перпендикуляра a к отрезку AB и докажем, что AM = BM.

Если точка M совпадает с серединой O отрезка AB, то справедливость равенства AM = BM очевидна. Если же M и O – различные точки, то прямоугольные треугольники OAM и OBM (рис. 107) равны по двум катетам, поэтому AM = BM. Теорема доказана.

В любой теореме различают две части: условие и заключение. Условие теоремы – это то, что дано, заключение – то, что требуется доказать. Рассмотрим, например, теорему об углах равнобедренного треугольника. Чтобы выделить в ней условие и заключение, сформулируем ее так: «если треугольник равнобедренный, то углы при его основании равны». Условием здесь является первая часть утверждения: «если треугольник равнобедренный», а заключением – вторая часть: «то углы при его основании равны». Можно сказать так: дан равнобедренный треугольник; требуется доказать, что углы при его основании равны.

Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением – ее условие. Обратной теореме об углах равнобедренного треугольника является теорема о признаке равнобедренного треугольника: если два угла треугольника равны, то этот треугольник равнобедренный.

Отметим, что если доказана какая-нибудь теорема, то из этого еще не следует справедливость обратного утверждения. Более того, обратное утверждение не всегда оказывается верным. Например, мы знаем, что если углы вертикальные, то они равны. Обратное утверждение: «если углы равны, то они вертикальные», конечно же, неверно.

Докажем теорему, обратную теореме о серединном перпендикуляре к отрезку.

Теорема. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.

Доказательство. Рассмотрим произвольную точку M, равноудаленную от концов отрезка AB, и докажем, что точка M лежит на серединном перпендикуляре a к этому отрезку.

Если точка M лежит на прямой AB, то она совпадает с серединой O отрезка AB, а значит, лежит на прямой a. Если же точка M не лежит на прямой AB, то точки A, B и M – вершины равнобедренного треугольника (рис. 108), так как AM = BM по условию. Отрезок MO – медиана этого треугольника, а следовательно, и высота, поэтому MO ⊥ AB. Таким образом, прямая MO – серединный перпендикуляр к отрезку AB, и точка M лежит на нем. Теорема доказана.

Следствие. Множество всех точек плоскости, каждая из которых равноудалена от концов отрезка, есть серединный перпендикуляр к этому отрезку.

Обозначим это множество буквой Ф. По теореме о серединном перпендикуляре к отрезку каждая точка серединного перпендикуляра принадлежит множеству Ф. А по обратной теореме каждая точка множества Ф принадлежит серединному перпендикуляру к отрезку. Следовательно, множество Ф и есть этот серединный перпендикуляр.

Множество всех точек, удовлетворяющих какому-либо условию, называют также геометрическим местом точек, удовлетворяющих этому условию. Можно сказать, что серединный перпендикуляр к отрезку – это геометрическое место точек, равноудаленных от его концов.

Источник

Голосование за лучший ответ

Бенефис мартовской кошки

Просветленный

(39699)

8 лет назад

Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.

Свойства серединных перпендикуляров треугольника
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.

Ангелина ГребенкинаУченик (101)

5 лет назад

Утверждение верное, но не объяснимое, что же такое “Серединный перпендикуляр” это пояснение было поверхностным. Была бы я, ученицей не читала б !

Алекс

Ученик

(195)

4 года назад

Евгения Тихомирова

Профи

(699)

4 года назад

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину отрезка и перпендикулярная к нему. На рисунке 106 прямая a – серединный перпендикуляр к отрезку AB. Докажем теорему о серединном перпендикуляре к отрезку.

Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

https://mthm.ru/images/geometry7/pic106-107.png

Кристина Глухова

Ученик

(132)

4 года назад

равиль давлетхузин

Профи

(537)

3 года назад

Даша Бец

Знаток

(275)

2 года назад

Источник