Какое свойство точек биссектрисы угла

2 июня 2018

Сегодня будет очень лёгкий урок. Мы рассмотрим всего один объект — биссектрису угла — и докажем важнейшее её свойство, которое очень пригодится нам в будущем.

Только не надо расслабляться: иногда ученики, желающие получить высокий балл на том же ОГЭ или ЕГЭ, на первом занятии даже не могут точно сформулировать определение биссектрисы.

И вместо того, чтобы заниматься действительно интересными задачами, мы тратим время на такие простые вещи. Поэтому читайте, смотрите — и берите на вооружение.:)

Для начала немного странный вопрос: что такое угол? Правильно: угол — это просто два луча, выходящих из одной точки. Например:

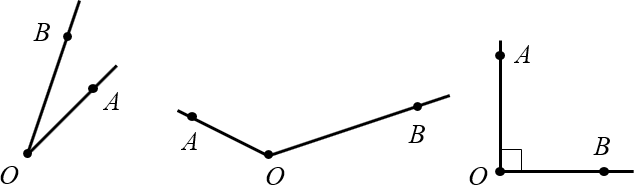Какое свойство точек биссектрисы угла Примеры углов: острый, тупой и прямой

Как видно из картинки, углы могут быть острыми, тупыми, прямыми — это сейчас неважно. Часто для удобства на каждом луче отмечают дополнительную точку и говорят, мол, перед нами угол $AOB$ (записывается как $angle AOB$).

Капитан очевидность как бы намекает, что помимо лучей $OA$ и $OB$ из точки $O$ всегда можно провести ещё кучу лучей. Но среди них будет один особенный — его-то и называют биссектрисой.

Определение. Биссектриса угла — это луч, который выходит из вершины этого угла и делит угол пополам.
Для приведённых выше углов биссектрисы будут выглядеть так:
Примеры биссектрис для острого, тупого и прямого угла

Поскольку на реальных чертежах далеко не всегда очевидно, что некий луч (в нашем случае это луч $OM$) разбивает исходный угол на два равных, в геометрии принято помечать равные углы одинаковым количеством дуг (у нас на чертеже это 1 дуга для острого угла, две — для тупого, три — для прямого).

Хорошо, с определением разобрались. Теперь нужно понять, какие свойства есть у биссектрисы.

Основное свойство биссектрисы угла

На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:

Теорема. Биссектриса угла — это геометрическое место точек, равноудалённых от сторон данного угла.

В переводе с математического на русский это означает сразу два факта:

Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.

Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:

Определение. Расстояние от точки до прямой — это длина перпендикуляра, проведённого из данной точки к этой прямой.

Например, рассмотрим прямую $l$ и точку $A$, не лежащую на этой прямой. Проведём перпендикуляр $AH$, где $Hin l$. Тогда длина этого перпендикуляра и будет расстоянием от точки $A$ до прямой $l$.

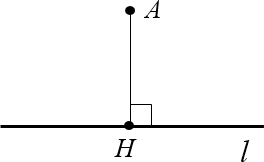Какое свойство точек биссектрисы угла Графическое представление расстояния от точки до прямой

Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:

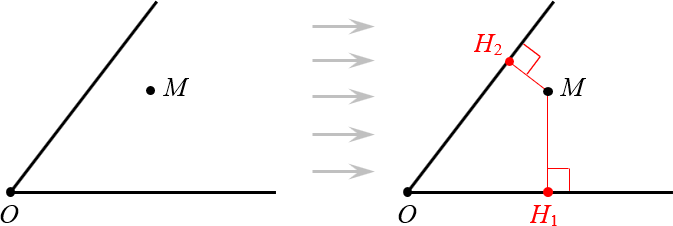Какое свойство точек биссектрисы угла Определяем расстояние от точки до сторон угла

Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.

Как и обещал, разобьём доказательство на две части:

1. Расстояния от точки на биссектрисе до сторон угла одинаковы

Рассмотрим произвольный угол с вершиной $O$ и биссектрисой $OM$:

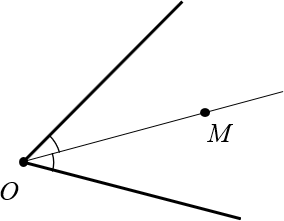
Какое свойство точек биссектрисы угла

Докажем, что эта самая точка $M$ находится на одинаковом расстоянии от сторон угла.

Доказательство. Проведём из точки $M$ перпендикуляры к сторонам угла. Назовём их $M{{H}_{1}}$ и $M{{H}_{2}}$:
Провели перпендикуляры к сторонам угла
Получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. У них общая гипотенуза $OM$ и равные углы:
$angle MO{{H}_{1}}=angle MO{{H}_{2}}$ по условию (поскольку $OM$ — биссектриса);
$angle M{{H}_{1}}O=angle M{{H}_{2}}O=90{}^circ $ по построению;
$angle OM{{H}_{1}}=angle OM{{H}_{2}}=90{}^circ -angle MO{{H}_{1}}$, поскольку сумма острых углов прямоугольного треугольника всегда равна 90 градусов.
Следовательно, треугольники равны по стороне и двум прилежащим углам (см. признаки равенства треугольников). Поэтому, в частности, $M{{H}_{2}}=M{{H}_{1}}$, т.е. расстояния от точки $O$ до сторон угла действительно равны. Что и требовалось доказать.:)

2. Если расстояния равны, то точка лежит на биссектрисе

Теперь обратная ситуация. Пусть дан угол $O$ и точка $M$, равноудалённая от сторон этого угла:

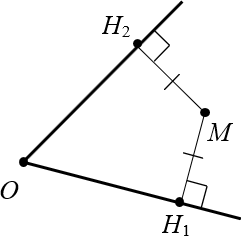
Какое свойство точек биссектрисы угла

Докажем, что луч $OM$ — биссектриса, т.е. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$.

Доказательство. Для начала проведём этот самый луч $OM$, иначе доказывать будет нечего:
Провели луч $OM$ внутри угла
Снова получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. Очевидно, что они равны, поскольку:
Гипотенуза $OM$ — общая;
Катеты $M{{H}_{1}}=M{{H}_{2}}$ по условию (ведь точка $M$ равноудалена от сторон угла);
Оставшиеся катеты тоже равны, т.к. по теореме Пифагора $OH_{1}^{2}=OH_{2}^{2}=O{{M}^{2}}-MH_{1}^{2}$.
Следовательно, треугольники $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$ по трём сторонам. В частности, равны их углы: $angle MO{{H}_{1}}=angle MO{{H}_{2}}$. А это как раз и означает, что $OM$ — биссектриса.
В заключение доказательства отметим красными дугами образовавшиеся равные углы:
Биссектриса разбила угол $angle {{H}_{1}}O{{H}_{2}}$ на два равных

Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)

Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.

Смотрите также:

Высота в треугольнике
Основное свойство биссектрисы угла в треугольнике и его применение для решения задач
Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
Правила вычисления производных
Сводный тест по задачам B15 (2 вариант)
Симметрия корней и оптимизация ответов в тригонометрии

Источник

Базовым понятием и одним из наиболее интересных и полезных объектов школьной математики является биссектриса. С её помощью доказываются многие положения планиметрии, упрощается решение задач.

Известные свойства позволяют рассматривать геометрические фигуры с разных точек зрения. Появляется вариативность при выборе пути доказательств.

Становится возможным использование инструмента алгебры, например, свойство пропорции, нахождение неизвестных величин, решение алгебраических уравнений при рассмотрении геометрических вопросов.

Что такое биссектриса в геометрии

Биссектриса угла

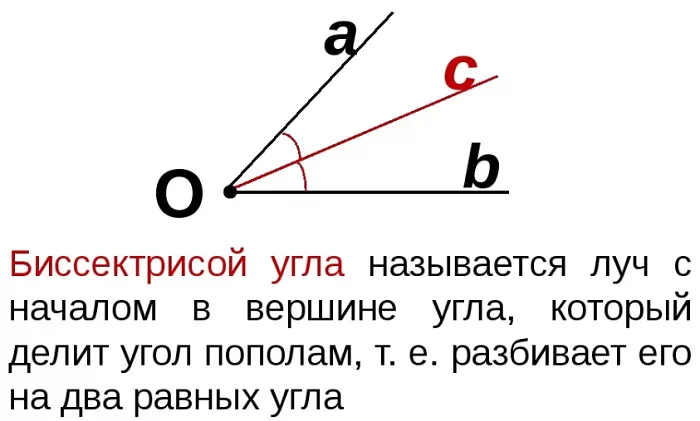
Рассматривают луч, выходящий из вершины угла или его часть (отрезок), который делит угол пополам. Такой луч (или, соответственно, отрезок) называется биссектрисой.

Биссектриса треугольника

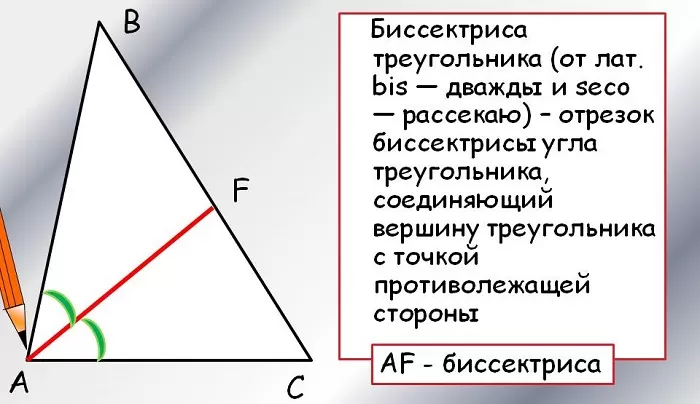
Часто для треугольников определение немного сужают, говоря об отрезке, соединяющем вершину угла, делящем его пополам, с точкой на противолежащей стороне. При этом рассматривается внутренняя область фигуры.

В то же время, часто при решении задач используются прямые, делящие внешние углы на два равных.

<br />

Биссектриса прямоугольного треугольника

Для прямоугольного треугольника одна из биссектрис образует равные углы, величины которых хорошо просчитываются (45 градусов).

Биссектриса в прямоугольном треугольнике

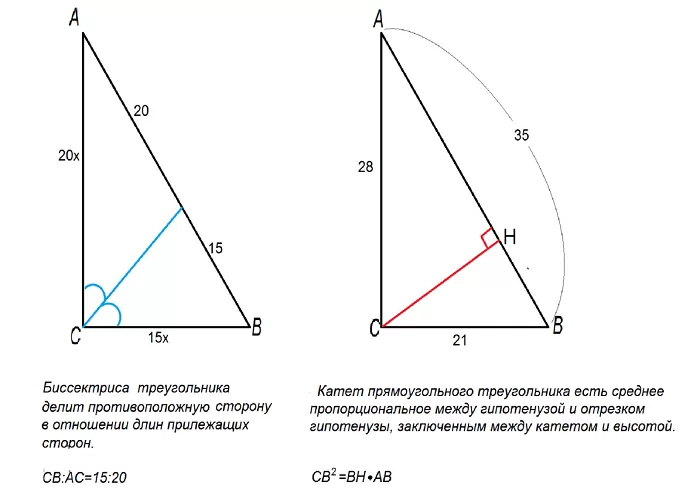
Это помогает вычислять углы при решении задач, связанных с фигурами, которые можно представить в виде прямоугольных треугольников или прямоугольников.

Биссектрисы тупоугольного треугольника

В тупоугольном треугольнике биссектриса делит больший угол на равные части, величина которых меньше 900.

Свойства биссектрисы треугольника

1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.

2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон.

100

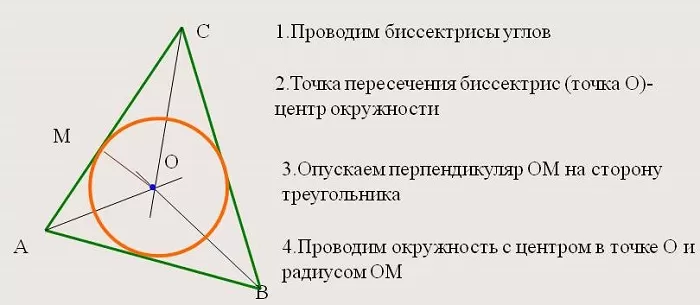
Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.

Благодаря этому утверждению, легко доказывается следующее правило:

Площадь описанного многоугольника равна:

S = p∗r

где p – полупериметр, а r – радиус вписанной окружности.

Это позволяет находить решение не только планиметрических, но и стереометрических задач.

Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;

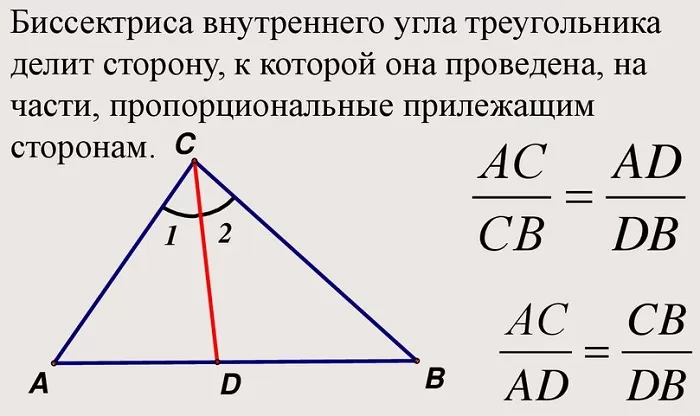
3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.

Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;

4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.

В этом случае основание параллельно внешней биссектрисе.

Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;

5. Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;

6. У правильного треугольника все внешние биссектрисы параллельны сторонам;

7. Выделяют несколько особенностей, среди которых есть следующая теорема:

«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».

120

Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;

8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.

<br />

Все формулы биссектрисы в треугольнике

В зависимости от исходных данных, длина биссектрисы, проведённой к стороне C, lc, равна:

Примеры решения задач

Задача №1

В ΔABC ∠C = 90°, проведена биссектриса острого угла. Отрезок, соединяющий её основание с точкой пересечения медиан, перпендикулярен катету. Найти углы заданной фигуры.

Решение.

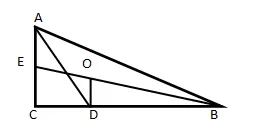
Пусть ∠ACB = 90°, AD – биссектриса, BE – медиана, O – точка пересечения медиан, OD⊥BC.

Тогда OE : OB = 1 : 2по свойству медиан.

Так как OD⊥BC, то ODIIOC, следовательно, ΔBOD ∼ ΔBEC по второму признаку подобия, поэтому, по свойству подобных фигур, CD : DB = 1 : 2.

Это означает, что CA : AB = 1 : 2.

Так как катет равен половине гипотенузы, то ∠ABC = 30°, откуда ∠CAB = 60°.

Ответ: 90°, 60°, 30°.

Задача №2

Диагональ параллелограмма делит его острый угол пополам. Доказать, что этот параллелограмм является ромбом.

Доказательство.

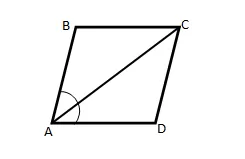
Так как ABCD – параллелограмм, то ∠DAC = ∠ACB, как накрест лежащие при параллельных прямых AD, BC и секущей AC.

По условию, ∠DAC = ∠ACB = ∠BAC, поэтому ΔACB равнобедренный, то есть AB = BC, следовательно, ABCD – ромб.

Доказано.

<br />

Источник

Презентация на тему: ” Свойство точек биссектрисы угла.. Основополагающий вопрос – Как расположены точки биссектрисы угла от его сторон? – Какой фигурой будет геометрическое.” — Транскрипт:

Свойство точек биссектрисы угла.

Основополагающий вопрос – Как расположены точки биссектрисы угла от его сторон? – Какой фигурой будет геометрическое место точек, равноудалённых от сторон угла?

Проблемный вопрос – Где будут находиться точки, равноудалённые от сторон угла? – Возможно ли что точки, одинаково удаленные от сторон угла находятся на его биссектрисе?

? ? ? – Может никакой фигуры не получится? – Все точки будут беспорядочно «скакать» и мы не сможем определить фигуру? – А зачем это нужно исследовать? – Чем эти знания могут нам помочь в дальнейшем?

План работы Построить модель угла прямого, тупого, острого. С помощью транспортира провести биссектрису углов. Проделать отверстия на биссектрисе. Через дырочки протянуть нить с грузиком.

Подготовительный этап. Построить модель угла прямого, тупого, острого. С помощью транспортира провести биссектрису углов. Проделать отверстия на биссектрисе. Через дырочки протянуть нить с грузиком.

Попробуй выполнить модель как на рисунке

Как можно однозначно определить расстояние от точки до прямой? Выбери длину нити и соедини её с точкой на стороне угла. Сколько таких точек можно указать?

Сколько таких точек можно указать? Как найти единственную точку?

Вывод Точки биссектрисы угла ……………………………………………… ………….

Источник

Тема: Свойство биссектрисы угла.

Цели:Рассмотрение теоремы о свойстве биссектрисы угла и применение данной теоремы при решении задач.

Задачи:

1. Рассмотреть теорему о свойстве биссектрисы угла и её следствие.

2. Учить применять данные теоремы и следствие при решении задач.

3. Формировать умения применять известные знания в незнакомой ситуации, сравнивать, анализировать, обобщать.

4. Продолжать развивать познавательную активность, умение формулировать свои выводы и доказывать их.

5. Воспитывать уверенность в себе, познавательный интерес.

Оборудование: ПК, презентация, чертёжные инструменты.

Ход урока

I. Организационный момент. Объявление темы и постановка целей урока совместно с учащимися.

II. Проверка домашнего задания.

Визуально проверяется наличие домашнего задания в тетради

III. Актуализация опорных знаний

Для того, чтобы начать изучение нового материала, нам придётся опереться на уже изученный материал.

1. Какие линии в треугольнике вам известны? К числу линий, изучаемых в школьном курсе геометрии, относятся:

• высоты треугольника;

• медианы треугольника;

• биссектрисы треугольника;

• серединные перпендикуляры к сторонам треугольника.

2. Кто напомнит обобщенную теорему Фалеса?

Если на одной стороне угла отложить несколько отрезков и через их концы провести параллельные прямые, то на другой стороне угла отложатся отрезки, пропорциональные данным.

Повторение определений путём фронтальной беседы.

III. Мотивация изучения материала

В старших классах каждый школьник

Изучает треугольник.

Три каких-то уголка,

А работы на века.

И опять треугольник! Треугольник в геометрии играет особую роль. Без преувеличения можно сказать, что вся или почти вся геометрия строится на треугольнике.

IV. Изучение нового материала.

Доказательство:

V. Историческая справка.

Удивительно, но треугольник, несмотря на свою простоту, является неисчерпаемым объектом изучения – никто даже в наше время не осмелится сказать, что изучил и знает все свойства треугольника. (Слайд 3).

–А какие треугольники мы с вами рассматривали? (Слайд 4).

Ожидаемые ответы: равнобедренный, равносторонний, тупоугольный, прямоугольный, остроугольный.

–Сегодня мы с вами очень кратко ознакомимся с треугольниками, которые имеют своё собственное «имя», или носят имя того, кто их открыл или исследовал. (Слайд 4).

Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.Египетский треугольник с соотношением сторон 3:4:5 применялся египтянами землемерами и архитекторами для построения прямых углов. Несмотря на возраст, это способ построения прямого угла активно используется строителями и теперь. (Слайд 4, 6).

Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. (Слайды 4, 7).

Треугольник Рёло – это геометрическая фигура, образованная пересечением трёх равных кругов одинакового радиуса с центрами в вершинах равностороннего треугольника. Сверло, сделанное на основе треугольника Рёло, позволяет сверлить квадратные отверстия (с точностью в 2%). (Слайды 4, 8).

Один из самых загадочных и интересных треугольников – “Бермудский треугольник”. Еще это место называют аномальной зоной. На самом деле это место, которое традиционно считается самым ужасным, самым жутким местом планеты. Здесь бесследно исчезало множество кораблей и самолетов – большинство из них после 1945 года. Здесь погибло более тысячи человек. Однако при поисках никого и ничего не удалось обнаружить. Бермудский треугольник не имеет четких границ, нельзя найти на карте его точное обозначение. Разные ученые определяют его местоположение на свое усмотрение. Самое распространенное его определение – это область в Атлантическом океане между Бермудами, Пуэрто-Рико и Майами. Общая площадь – 1 млн. квадратных километров. Однако название этой области тоже условное, поэтому название “Бермудский треугольник” не является географическим. (Слайды 4, 9).

Треугольник Пенроуза… Эта фигура –возможно, первый опубликованный в печати невозможный объект. Она появилась в 1958 году в журнале. в статье под заголовком “Удивительные фигуры, особый вид оптических иллюзий”. Ее авторы, отец и сын Лайонелл и Роджер Пенроузы. Невозможный» треугольник, треугольник Пенроуза, увековечен в виде статуи в городе Перт (Австралия). Созданный усилиями художника Брайна МакКея и архитектора Ахмада Абаса, он был воздвигнут в парке Клайзебрук в 1999 году и теперь все проезжающие мимо могут видеть «невозможную» фигуру. (Слайды 4, 10).
Интересно! (Слайд 11).

–А теперь вернёмся к теме нашего урока.

VI. Первичное закрепление знаний.

Учебник: стр.138, № 318, 320, 321

VII. Подведение итогов урока.

Решение задачи, данной в начале урока

Оценивание работы учащихся и выставление отметок в журнал

VIII. Домашнее задание.

Глава 3, §22, № 319

Источник