Какое свойство силы упругости
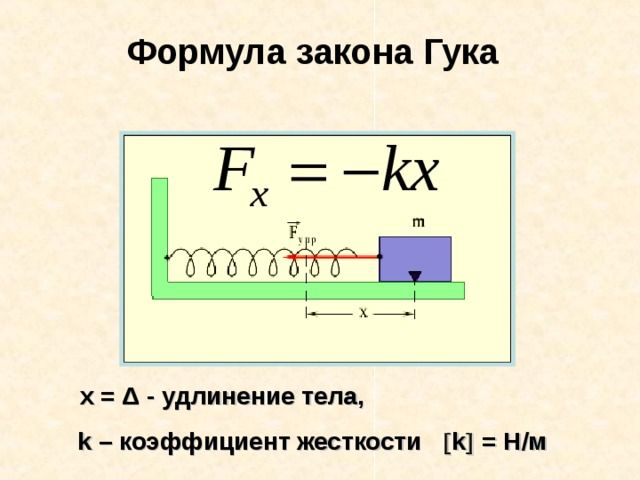
Сила упругости
Любое тело, когда его деформируют и оказывают внешнее воздействие, сопротивляется и стремиться восстановить прежние форму и размеры. Это происходит по причине электромагнитного взаимодействия в теле на молекулярном уровне.
Деформация – изменение положения частиц тела друг относительно друга. Результат деформации – изменение межатомных расстояний и перегруппировка блоков атомов.
Определение. Что такое сила упругости?
Сила упругости – сила, возникающая при деформации в теле и стремящаяся вернуть тело в начальное состояние.
Рассмотрим простейшие деформации – растяжение и сжатие
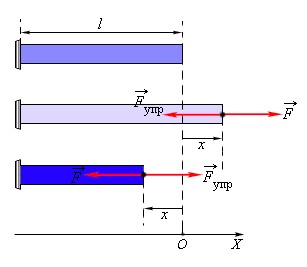
На рисунке показано, как действует сила упругости, когда мы сжимаем или растягиваем стержень.
Закон Гука
Для малых деформаций x≪ l справедлив закон Гука.
Закон Гука
Деформация, возникающая в упругом теле, пропорциональна приложенной к телу силе.
Fупр=-kx
Здесь k – коэффициент пропорциональности, называемый жесткостью. Единица измерения жесткости системе СИ Ньютон на метр. Жесткость зависит от материала тела, его формы и размеров.
Знак минус показывает, что сила упругости противодействует внешней силе и стремится вернуть тело в первоначальное состояние.
Существуют и другие формы записи закона Гука. Относительной деформацией тела называется отношение ε=xl. Напряжением в теле называется отношение σ=-FупрS. Здесь S – площадь поперечного сечения деформированного тела. Вторая формулировка закона Гука: относительная деформация пропорциональна напряжению.
ε=σE.
Здесь E – так называемый модуль Юнга, который не зависит от формы и размеров тела, а зависит только от свойств материала. Значение модуля Юнга для различных материалов широко варьируется. Например, для стали E≈2·1011 Нм2, а для резины E≈2·106 Нм2
Закон Гука можно обобщить для случая сложных деформаций. Рассмотрим деформацию изгиба стержня. При такой деформации изгиба сила упругости пропорциональна прогибу стержня.
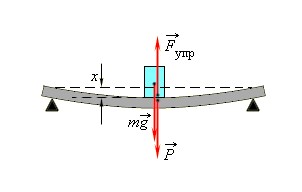
Концы стержня лежат на двух опорах, которые действуют на тело с силой N→, называемой силой нормальной реакции опоры. Почему нормальной? Потому что эта сила направлена перпендикулярно (нормально) поверхности соприкосновения.
Если стержень лежит на столе, сила нормальной реакции опоры направлена вертикально вверх, противоположно силе тяжести, которую она уравновешивает.
Вес тела – это сила, с которой оно действует на опору.
Силу упругости часто рассматривают в контексте растяжения или сжатия пружины. Это распространенный пример, который часто встречается не только в теории, но и на практике. Пружины используются для измерения величины сил. Прибор, предназначенный для этого – динамаметр.
Динамометр – пружина, растяжение которой проградуированно в единицах силы. Характерное свойство пружин заключается в том, что закон Гука для них применим при достаточно большом изменении длины.
При сжатии и растяжении пружины действует закон Гука, возникают упругие силы, пропорциональные изменению длины пружины и ее жесткости (коэффициента k).
В отличие от пружин стержни и проволоки подчиняются закону Гука в очень узких пределах. Так, при относительной дефомации больше 1% в материале возникают необратимые именения – текучесть и разрушения.
Источник
Сила упругости всегда является результатом деформации тела. Данная сила всегда пытается вернуть деформированное тело в исходное положение. Что же такое сила упругости, и при каких условиях она возникает?

Общая характеристика силы упругости
Сила упругости возникает при деформации тел, например, при растяжении или сжатии пружины. Деформация – это изменение формы и размеров тела.
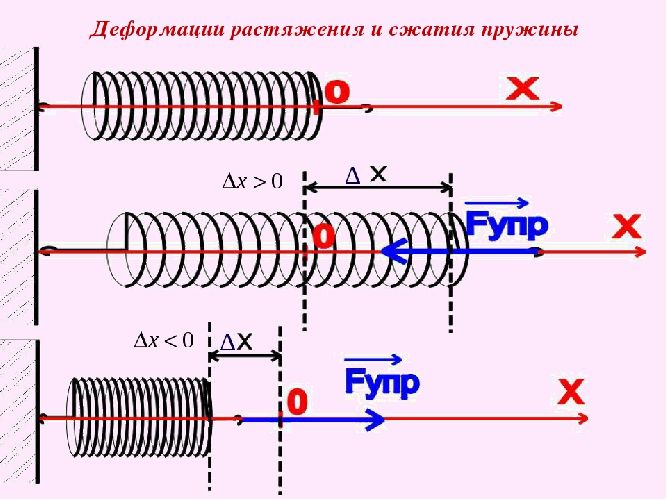
Рис. 1. Сила упругости при деформации пружины.
Если исчезнет деформация тела, то сила упругости тоже исчезнет
Причиной возникновения сил упругости являются силы притяжения и отталкивания между частицами (молекулами или атомами), из которых состоят все тела. Если слегка увеличить расстояние между частицами, то силы взаимодействия оказываются силами притяжения между ними. Если же расстояние между частицами немного уменьшить, они становятся силами отталкивания. Сила упругости, действующая на тело, связана с деформацией тела следующим образом:
$F упр=-kx$,
где F упр. – модуль силы упругости, х – удлинение тела (расстояние, на которое изменяется первоначальная длина тела), k – коэффициент пропорциональности, называемый жесткостью пружины, измеряемый в Н/м. Данная формула силы упругости служит выражением закона Гука. Определение закона Гука выражается следующим образом: сила упругости, возникающая при деформации тела, пропорциональна удлинению тела и направлена противоположно перемещению частиц тела относительно других частиц при деформации.

Рис. 2. Формула закон Гука.
Прямую пропорциональную зависимость между силой упругости и удлинением используют в динамометрах – приборах для измерения силы. Силы упругости работают в технике и природе: в часовых механизмах, в амортизаторах на транспорте, в канатах и тросах, в человеческих костях и мышцах.
Свойства силы упругости
К силам упругости относятся сила реакции опоры и веса тела. Сила реакции (N) со стороны опоры на тело возникает, когда тело кладут на какую-нибудь поверхность (опору).
Если тело подвешивают на нити, то эта же самая сила называется силой натяжения нити (Т).
Силы упругости имеет ряд особенностей:
- возникают при деформации
- возникают одновременно у двух тел
- перпендикулярны поверхности
- противоположны по направлению смещению.
Вес тела (P) – это сила, с которой тело действует на горизонтальную опору или вертикальный подвес, вследствие своего притяжения к Земле.
Вес тела обозначается буквой P и измеряется в Ньютонах.
Если опора тела горизонтальна и неподвижна, то вес такого тела численно равен силе тяжести, действующей на это тело и равен P=mg
Если же тело движется вверх с ускорением а, то вес этого тела больше веса покоящегося тела и равен $P=(g+a)m$
А если же тело с ускорением а движется вниз, то его вес $P =(g-a)m$
При равенстве ускорения тела и ускорения свободного падения вес тела равен нулю. Это состояние невесомости.
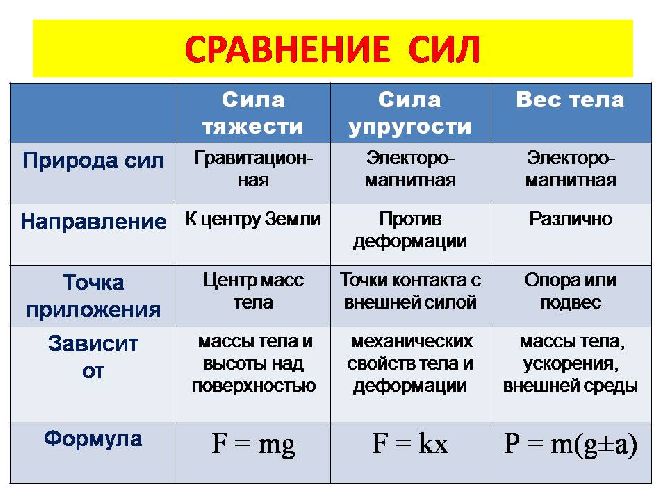
Рис. 3. Таблица сравнение силы упругости с другими силами.
Что мы узнали?
Тема «Сила упругости» является важным этапом в познании физики как науки. Силы упругости – это силы, возникающие в теле при его упругой деформации и направленные в сторону, противоположную смещению частиц при деформации. Сила упругости не существует без деформации тела. Также к силам упругости относятся сила реакции опоры и веса тела.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-

Мария Солнышкина
9/10
Оценка доклада
Средняя оценка: 4.4. Всего получено оценок: 110.
Источник
Сила – это количественная мера взаимодействия тел. В рамках классической механики мы имеем дело со следующими видами сил: силами инерции, гравитационными, электростатическими, упругими, силами трения и сопротивления. Объектами воздействия классических сил являются м.т., с.м.т., твердое тело, сплошная среда (твердое вещество, газ, жидкость).
Силы упругости, силы трения и сопротивления определяются взаимодействиеями между молекулами вещества и имеют в своей основе электромагнитное происхождение и действуют в масштабах межмолекулярных расстояний.
Закон Гука
Закон Гука применим к деформируемым объектам, возвращающимся к исходному состоянию после снятия силы. Например, для растягивающейся пружины справедлива формула силы
F = kx, (1)
где F – действующая сила,
k – коэффициент пропорциональности, или жесткость пружины,
x – растяжение пружины.
Кроме линейных объектов типа пружины, на практике встречается множество других типов деформируемых объектов, по отношению к которым можно применять закон Гука. Только в этом случае коэффициент k может быть тензором 2–го порядка соответствующей размерности. Движение при этом обратимо.
Деформацией называют изменение формы, размеров или объема тела. Деформация может быть вызвана действием на тело приложенных к нему внешних сил. Если после прекращения действия сил тело возвращается в прежнее состояние (деформация исчезает), то деформация называется упругой. Деформации, сохраняющиеся и после того, как внешние силы перестали действовать на тело – пластическими. Обычно деформация бывает упругой, если ее величина не превосходит определенного предела (предела упругости). Внутри такого деформированного тела возникают силы, называемые силами упругости.
Различают деформации растяжения или сжатия (одностороннего или всестороннего), изгиба, кручения и сдвига.
Силы упругости действуют в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. В случае одностороннего растяжения или сжатия сила упругости направлена вдоль прямой, по которой действует внешняя сила, вызывающая деформацию тела, противоположно направлению этой силы и перпендикулярно поверхности тела.
Природа упругих сил электрическая. При деформациях твердого тела его частицы (атомы, молекулы, ионы), находящиеся в узлах кристаллической решетки, смещаются из своих положений равновесия. Этому смещению противодействуют силы взаимодействия между частицами твердого тела, удерживающие эти частицы на определенном расстоянии друг от друга. Поэтому при любом виде упругой деформации в теле возникают внутренние силы, препятствующие его деформации. Связь между силой упругости и упругой деформацией тела (при малых деформациях) была экспериментально установлена английским физиком Гуком.
Закон Гука для одностороннего растяжения (сжатия) формулируют так: сила упругости, возникающая при деформации тела, пропорциональна удлинению этого тела. Опытным путем установлено, что при малых деформациях упругая сила пропорциональна величине деформации. Например, при растяжении пружины на величину Δlупругая сила F вдоль оси пружины будет равна
F = –kΔl, (2)
где F – сила упругости;
Δl – удлинение (деформация) тела;
k – коэффициент пропорциональности, зависящий от размеров и материала тела, называемый жесткостью. Единица жесткости в СИ – ньютон на метр (Н/м).
Знак “–” в формуле (2) указывает, что направление силы противоположно направлению деформации (при растяжении пружины сила F сжимает ее и наоборот, при сжатии растягивает).
Упругую силу принято характеризовать не ее непосредственной величиной F, а отношением F к площади поверхности S, через которую она действует. Это отношение называют напряжением. В случае, когда сила F перпендикулярна поверхности S, напряжение называют нормальным. Его обозначают σ. Напряжение измеряют в паскалях [Па]. (1 Па = 1 Н / 1 м2).
Деформацию твердых тел чаще характеризуют не абсолютным изменением длины Δl, а относительным удлинением ε (3)
где l – длина тела. ε – безразмерная величина.
При малых деформациях относительное удлинение пропорционально нормальному напряжению. Эту связь деформации и напряжения также называют законом Гука. Его принято записывать в следующей форме (4):
Коэффициент пропорциональности Е в законе Гука характеризует упругость данного материала и называется модулем (продольной) упругости (модулем Юнга). Модуль Юнга численно равен такому нормальному напряжению, которое должно было бы возникнуть в теле при увеличении его длины в 2 раза (если бы для такой большой деформации выполнялся закон Гука). Модуль упругости выражается в паскалях.
Диаграмма растяжения
Используя формулу (3), (4), по экспериментальным значениям относительного удлинения ε можно вычислить соответствующие им значения нормального напряжения σ, возникающего в деформированном теле, и построить график зависимости σ от ε. Этот график называют диаграммой растяжения. Подобный график для металлического образца изображен на рис. 1.
Рис. 1. График деформации реального тела.
На участке 0–1 график имеет вид прямой, проходящей через начало координат. Это значит, что до определенного значения напряжения σп деформация является упругой и выполняется закон Гука, т. е. нормальное напряжение пропорционально относительному удлинению. Максимальное значение нормального напряжения σп, при котором еще выполняется закон Гука, называют пределом пропорциональности.
При дальнейшем увеличении нагрузки зависимость напряжения от относительного удлинения становится нелинейной (участок 1–2), хотя упругие свойства тела еще сохраняются. Максимальное значение нормального напряжения, при котором еще не возникает остаточная деформация, называют пределом упругости. (Предел упругости лишь на сотые доли процента превышает предел пропорциональности.) Увеличение нагрузки выше предела упругости (участок 2–3) приводит к тому, что деформация становится остаточной.
Затем образец начинает удлиняться практически при постоянном напряжении (участок 3–4 графика). Это явление называют текучестью материала. Нормальное напряжение σт, при котором остаточная деформация достигает заданного значения, называют пределом текучести.
При напряжениях, превышающих предел текучести, упругие свойства тела в известной мере восстанавливаются, и оно вновь начинает сопротивляться деформации (участок 4–5 графика). Максимальное значение нормального напряжения σпр, при превышении которого происходит разрыв образца, называют пределом прочности.
Таблица 1. Пример таблицы модулей упругости металлов
—————————————————————————————-
Ссылка на мою статью Как написать формулы в статье на Дзен?
Мои странички на Дзен: https://zen.yandex.ru/id/5e036c95fc69ab00aecfe6e9
Если хотите узнать, что обозначает слово или словосочетание, в ОПЕРЕ выделите это слово(сочетание), нажмите правую клавишу мыши и выберите “Искать в …”, далее – “Yandex”. Если это текстовая ссылка – выделите ее, нажмите правую клавишу мыши, выберите “перейти …”. Все! О-ля-ля!
Если вам понравилась статья, то поставьте “лайк” и подпишитесь на канал! Если не понравилась – все равно комментируйте и подписывайтесь. Этим вы поможете каналу. И делитесь ссылками в ваших соцсетях!
Источник
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: силы в механике, сила упругости, закон Гука.
Как мы знаем, в правой части второго закона Ньютона стоит равнодействующая (то есть векторная сумма) всех сил, приложенных к телу. Теперь нам предстоит изучить силы взаимодействия тел в механике. Их три вида: сила упругости, гравитационная сила и сила трения. Начинаем с силы упругости.
Деформация.
Силы упругости возникают при деформациях тел. Деформация – это изменение формы и размеров тела. К деформациям относятся растяжение, сжатие, кручение, сдвиг и изгиб.
Деформации бывают упругими и пластическими. Упругая деформация полностью исчезает после прекращения действия вызывающих её внешних сил, так что тело полностью восстанавливает форму и размеры. Пластическая деформация сохраняется (быть может, частично) после снятия внешней нагрузки, и тело уже не возвращается к прежним размерам и форме.
Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение (это силы, действующие между ядрами и электронами соседних атомов). Силы взаимодействия зависят о расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается.
Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела.
Сила упругости – это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Сила упругости:
1. действует между соседними слоями деформированного тела и приложена к каждому слою;
2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример – сила реакции опоры).
Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти силы зависят не от величины деформации, а от скорости её возникновения. Изучение таких сил
выходит далеко за рамки школьной программы.
В школьной физике рассматриваются растяжения нитей и тросов, а также растяжения и сжатия пружин и стержней. Во всех этих случаях силы упругости направлены вдоль осей данных тел.
Закон Гука.
Деформация называется малой, если изменение размеров тела много меньше его первоначальных размеров. При малых деформациях зависимость силы упругости от величины деформации оказывается линейной.
Закон Гука. Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину , сила упругости даётся формулой:
(1)
где – коэффициент жёсткости пружины.
Коэффициент жёсткости зависит не только от материала пружины, но также от её формы и размеров.
Из формулы (1) следует, что график зависимости силы упругости от (малой) деформации является прямой линией (рис. 1 ):
 |
| Рис. 1. Закон Гука |
Коэффициент жёсткости – о угловой коэффициент в уравнении прямой . Поэтому справедливо равенство:
,
где – угол наклона данной прямой к оси абсцисс. Это равенство удобно использовать при экспериментальном нахождении величины .
Подчеркнём ещё раз, что закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела. Когда деформации перестают быть малыми, эта зависимость перестаёт быть линейной и приобретает более сложный вид. Соответственно, прямая линия на рис. 1 – это лишь небольшой начальный участок криволинейного графика, описывающего зависимость от при всех значениях деформации .
Модуль Юнга.
В частном случае малых деформаций стержней имеется более детальная формула, уточняющая общий вид ( 1 ) закона Гука.
Именно, если стержень длиной и площадью поперечного сечения растянуть или сжать
на величину , то для силы упругости справедлива формула:
.
Здесь – модуль Юнга материала стержня. Этот коэффициент уже не зависит от геометрических размеров стержня. Модули Юнга различных веществ приведены в справочных таблицах.
Источник
Изменение размеров и формы тел под
действием приложенных сил называется деформацией.
Если после прекращения действия сил, вызвавших деформацию, тело принимает
первоначальные размеры и форму, деформация называется упругой. Упругие деформации происходят в том
случае, если сила, обусловившая деформацию, не превосходит некоторый,
определенный для каждого конкретного тела предел. При превышении этого предела
тело получает остаточные (пластические) деформации, т.е. такие
деформации, которые сохраняются и после прекращения действия силы. Все
возможные виды упругих деформаций твердого тела могут быть сведены к двум
основным: растяжению-сжатию и сдвигу.
Диаграмма деформации.
Качественное поведение функциональной связи между относительной деформацией ε и напряжением σ представлено графически на рис. 16. При малых деформациях
(прямая линия 0-П) наблюдается область пропорциональной упругой деформации.
Здесь выполняется закон Гука. В области П-У деформация – также упругая, но
закон Гука не справедлив. Начиная с точки У, вплоть до точки Т наблюдается
область остаточных неупругих деформаций. Интервалу Т-Р соответствует область
текучести, когда приложение незначительного усилия приводит к повышенной
необратимой деформации. Вблизи точки Р текучесть прекращается, и для дальнейшего
деформирования тела требуется приложение повышенного усилия. Однако это
дополнительное усилие приводит к разрушению тела. Ниже перечислены названия
особых точек и областей деформации:
П – предельная точка пропорциональной деформации,
 У – предел упругости,
У – предел упругости,
0-У – область упругих деформаций,
Т – предел текучести,
У-Т – область остаточных деформаций,
Т-Р – область текучести,
Р – предел прочности, точка разрыва.
Рис. 16
Продольное
растяжение-сжатие (рис. 17 и 18). Если
к концам однородного стержня постоянного сечения приложить направленные вдоль
его оси силы F1 и F2, действие которых равномерно
распределено по всему сечению, причем F1
= – F2, то
первоначальная длина стержня l
получит положительное (при растяжении), либо
отрицательное (при сжатии) приращение Δl = l
– l
и станет равной l.
При этом каждый произвольно выбранный элемент длины стержня δl получает приращение Δ(δl), пропорциональное его
длине, так что для всех элементов стержня отношение Δ(δl)/δl оказывается одним итем же. Естественно поэтому в
качестве величины, характеризующей деформацию стержня, взять относительное
изменение его длины: ε = Δl/l0.
Относительное удлинение ε является безразмерной
величиной. В случае растяжения оно положительно, а в случае сжатия отрицательно.
Закон
Гука для стержней из однородного материала–
относительное удлинение при упругой деформации пропорционально силе,
приходящейся на единицу площади поперечного сечения стержня:
ε = a∙F
/ S = a∙s.
Коэффициент пропорциональности aназывается
коэффициентом упругости (упругой податливости). Он зависит только
от свойств материала стержня. Величина s, равная отношению силы F к величине поверхности S, на которую сила действует, называется напряжением F / S = s. Если сила направлена по
нормали к поверхности, напряжение называется нормальным. Если сила направлена
по касательной к поверхности, на которую она действует, напряжение называется
тангенциальным (или касательным). (Нормальное напряжение принято обозначать
символом s,
тангенциальное – τ). Итак, относительное удлинение оказывается пропорциональным
нормальному напряжению, и коэффициент упругости aчисленно
равен относительному удлинению при напряжении, равном единице.
Наряду с коэффициентом упругости aдля
характеристики упругих свойств материала пользуются обратной ему величиной Е = 1/ɑ,
которая называется модулем Юнга.
Заменяя ɑчерез Е в формуле ε= ɑ∙s, получим другую форму
закона Гука:
= (1/Е) ∙s.


Рис. 17 Рис.
18 Рис. 19
Следовательно, модуль Юнга равен
нормальному напряжению, при котором относительное удлинение равно единице (т.
е. приращение длины Δl равно первоначальной
длине l0,если бы столь большие
упругие деформации были доступны). На самом деле, при значительно меньших
напряжениях происходит разрыв стержня, а предел упругости достигается еще
раньше.
С учетом формул s = F / S и = Δl /
l0 из
закона Гука
= s
/Е следует
формула упругой силы:
F
= (Е∙S / l0)×Δl = k∙Δl,
где k– постоянный для данного
стержня коэффициент, который для пружин называется жесткостью пружины.
Изменение длины стержня при деформации
сопровождается изменением ![]() относительным поперечным
относительным поперечным
расширением или сжатием:
ε‘ = Δ d /
d.
Обычно ε
и ε‘ имеют противоположные знаки: при
растяжении ε положительно, a ε‘
отрицательно, при сжатии
отрицательно, a ‘положительно.
Опыт дает, что в области упругих деформаций ε‘
пропорционален ε :
ε‘ = – μ.∙ε,
где μ–
коэффициент поперечного сжатия или коэффициент
Пуассона (положительный коэффициент, зависящий только от свойств
материала).
Деформация
сдвига (рис. 19). Возьмем однородное тело, имеющее
форму прямоугольного параллелепипеда, и приложим к его противолежащим граням
силы ![]() и
и ![]() (
(![]() = –
= – ![]() ),
),
направленные параллельно этим граням. Если действие сил будет равномерно
распределено по всей поверхности соответствующей грани S, то в любом сечении, параллельном этим
граням, возникнет тангенциальное напряжение τ = F
/ S.
Под действием напряжения тело деформируется так, что одна грань смещается
относительно другой грани на некоторое расстояние а. Если тело мысленно
разбить на элементарные горизонтальные слои, то каждый слой окажется сдвинутым
относительно соседних с ним слоев.
При деформации сдвига любая прямая,
первоначально перпендикулярная к горизонтальным слоям, повернется на некоторый
угол j.
Следовательно, отношение сдвига δа двух произвольно взятых
слоев к расстоянию между этими слоями δb будет одинаково для
любой пары слоев. Это отношение естественно
взять в качестве характеристики деформации
сдвига : ![]() .
.
Величина gназывается относительным сдвигом. В силу малости угла
j можно
положить tg j
≈ j.
Следовательно, относительный сдвиг gоказывается
равным углу сдвига j
(выраженному в радианах). Опыт показывает, что для малых деформаций
относительный сдвиг пропорционален тангенциальному напряжению:
![]()
Коэффициент G зависит
только от свойств материала и называется модулем
сдвига. Он равен такому тангенциальному напряжению, при котором угол
сдвига оказался бы равным 45° (tg j = 1), если бы при столь больших
деформациях не был превзойден предел упругости.
 Кручение
Кручение
круглого стержня (рис. 20). Если круглый стержень закрепить одним концом
неподвижно, а к другому концу приложить вращательный момент (момент пары сил) ![]() ,
,
имеющий
направление вдольоси стержня, то
стержень получит такую деформацию, при которой одно основание повернется по
отношению к другому на некоторый угол j.
Деформация кручения – это пример
неоднородного сдвига. Действительно, если мысленно разбить стержень на
элементарные слои, перпендикулярные к его оси, то
закручивание приведет к сдвигу
каждого из таких слоев по риотношению к соседним
слоям. Правда, этот сдвиг Рис. 20
будет неоднороден: участок слоя ΔS получает по отношению к аналогичному участку смежного слоя
тем большее смещение, чем дальше он отстоит от оси стержня. Угол
закручивания стержня определяется следующим
выражением: Рис. 48
 ,
,
где l –
длина стержня,
R – радиус его сечения, G – модуль
сдвига, М –
вращательный момент (момент сил).
Энергия
упругой деформации. Упруго деформированное
тело, например, растянутый или сжатый стержень, возвращаясь в начальное
состояние, может, подобно сжатой или растянутой пружине, совершить работу над
внешними телами, т.е. обладает некоторым запасом энергии. Поскольку эта энергия
обусловлена взаимным расположением элементов тела, она представляет собой
потенциальную энергию WП.
Запас энергии деформированного тела равен работе, которая совершается внешними
силами при деформации WП
= A. Вычислим энергию упруго
растянутого стержня. При растяжении на стержень необходимо действовать силой,
модуль которой определяется выражением F
= k∙Δl. Работа этой силы равна: ![]() , где буквой х
, где буквой х
обозначено абсолютное удлинение стержня, которое в процессе деформации
изменяется от 0 до Δl. Сила F, соответствующая
удлинению х,
согласно формуле F
= (Е∙S / l0)×Δl = k∙Δl, равна
F
= k∙x = (Е∙S / l0)× x.
Следовательно, 
Умножая числитель и знаменатель полученного выражения на l0,
заменяя затем отношение Δl /
l0 относительным
удлинением e
= Δl
/ l
и учитывая, наконец, что произведение S∙l равно объему стержня V, получим:
 .
.
Введем в рассмотрение плотность энергии w, которую определим как отношение
энергии ΔW
к тому объему ΔV,
в котором она заключена. Поскольку в нашем случае стержень однороден и деформация
является равномерной, т. е. одинаковой в разных точках стержня, энергия
распределена в стержне также равномерно с постоянной плотностью. Поэтому можно
считать, что выражение
![]()
определяет плотность энергии упругой деформации при
растяжении (или при сжатии). Аналогичным образом можно получить, что
плотность энергии упругой деформации при сдвиге равна:
![]() .
.
В области пропорциональной деформации справедливы
также эквивалентные формулы:
 и
и  .
.
Источник
