Какое свойство проводника характеризует его электрическое сопротивление
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 5 июля 2019;
проверки требуют 3 правки.
Электри́ческое сопротивле́ние — физическая величина, характеризующая свойство проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему[1]
Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
где
R — сопротивление, Ом;
U — разность электрических потенциалов (напряжение) на концах проводника, В;
I — сила тока, протекающего между концами проводника под действием разности потенциалов, А.
История[править | править код]
В 1826 г. Георг Ом экспериментальным путем открыл основной закон электрической цепи, научился вычислять сопротивление металлических проводников и вывел закон Ома. Таким образом, в первом периоде развития электротехники (1800 –1831 годы) были созданы предпосылки для ее развития, для последующих применений электрического тока.
Само понятие «сопротивление» появилось задолго до изысканий Георга Ома. Впервые этот термин применил и употребил русский ученый Василий Владимирович Петров. Он установил количественную зависимость силы тока от площади поперечного сечения проводника: он утверждал, что при использовании более толстой проволоки происходит «более сильное действие… и весьма скорое течение гальвани-вольтовской жидкости». Кроме того, Петров четко указал на то, что при увеличении сечения проводника (при употреблении одной и той же гальванической батареи) сила тока в нем возрастает.[2]
Единицы и размерности[править | править код]
Размерность электрического сопротивления в Международной системе величин: dim R = L2MT −3I −2. В Международной системе единиц (СИ), основанной на Международной системе величин, единицей сопротивления является ом (русское обозначение: Ом; международное: Ω). В системе СГС как таковой единица сопротивления не имеет специального названия, однако в её расширениях (СГСЭ, СГСМ и гауссова система единиц) используются[3]:
- статом (в СГСЭ и гауссовой системе, 1 statΩ = (109c−2) с/см = 898 755 178 736,818 Ом (точно) ≈ 8,98755·1011 Ом, равен сопротивлению проводника, через который под напряжением 1 статвольт течёт ток 1 статампер);
- абом (в СГСМ, 1 abΩ = 1·10−9 Ом = 1 наноом, равен сопротивлению проводника, через который под напряжением 1 абвольт течёт ток 1 абампер).
Размерность сопротивления в СГСЭ и гауссовой системе равна TL−1 (то есть совпадает с размерностью обратной скорости, с/см), в СГСМ — LT−1 (то есть совпадает с размерностью скорости, см/с)[4].
Обратной величиной по отношению к сопротивлению является электропроводность, единицей измерения которой в системе СИ служит сименс (1 См = 1 Ом−1), в системе СГСЭ (и гауссовой) статсименс и в СГСМ — абсименс[5].
Физика явления[править | править код]
Высокая электропроводность металлов связана с тем, что в них имеется большое количество носителей тока — электронов проводимости, образующихся из валентных электронов атомов металла, которые не принадлежат определённому атому. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решётки (на примесях, дефектах решётки, а также нарушениях периодической структуры, связанной с тепловыми колебаниями ионов). При этом электроны теряют импульс, а энергия их движения преобразуются во внутреннюю энергию кристаллической решётки, что и приводит к нагреванию проводника при прохождении по нему электрического тока.
В других средах (полупроводниках, диэлектриках, электролитах, неполярных жидкостях, газах и т. д.) в зависимости от природы носителей заряда физическая причина сопротивления может быть иной. Линейная зависимость, выраженная законом Ома, соблюдается не во всех случаях.
Сопротивление проводника при прочих равных условиях зависит от его геометрии и от удельного электрического сопротивления материала, из которого он состоит.
Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и вычисляется по формуле:
где ρ — удельное сопротивление вещества проводника, Ом·м, l — длина проводника, м, а S — площадь сечения, м².
Сопротивление однородного проводника также зависит от температуры.
Удельное сопротивление — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника единичной длины и единичной площади сечения.
Сопротивление металлов снижается при понижении температуры; при температурах порядка нескольких кельвинов сопротивление большинства металлов и сплавов стремится или становится равным нулю (эффект сверхпроводимости). Напротив, сопротивление полупроводников и изоляторов при снижении температуры (в некотором диапазоне) растёт. Сопротивление также меняется по мере увеличения тока/напряжения, протекающего через проводник/полупроводник.
Зависимость сопротивления от материала, длины и площади поперечного сечения проводника[править | править код]
В металле подвижными носителями зарядов являются свободные электроны. Можно считать, что при своем хаотическом движении они ведут себя подобно молекулам газа. Поэтому в классической физике свободные электроны в металлах называют электронным газом и в первом приближении считают, что к нему применимы законы, установленные для идеального газа.
Плотность электронного газа и строение кристаллической решетки зависят от рода металла. Поэтому сопротивление проводника должно зависеть от рода его вещества. Кроме того, оно должно еще зависеть от длины проводника, площади его поперечного сечения и от температуры.
Влияние сечения проводника на его сопротивление объясняется тем, что при уменьшении сечения поток электронов в проводнике при одной и той же силе тока становится более плотным, поэтому и взаимодействие электронов с частицами вещества в проводнике становится сильнее.
Из формулы
видно, что сопротивление проводника прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения. Величину ρ, характеризующую зависимость сопротивления проводника от материала, из которого он сделан, и от внешних условий, называют удельным сопротивлением вещества. Удельное сопротивление различных веществ при расчетах берут из таблиц.
Величину, обратную удельному сопротивлению, называют удельной проводимостью вещества и обозначают σ.
Сопротивление тела человека[править | править код]
- Для расчёта опасной величины силы тока, протекающего через человека при попадании его под электрическое напряжение частотой 50 Гц, сопротивление тела человека условно принимается равным 1 кОм[6]. Эта величина имеет малое отношение к реальному сопротивлению человеческого тела. В реальности сопротивление человека не является омическим, так как эта величина, во-первых, нелинейна по отношению к приложенному напряжению, во-вторых меняется во времени, в третьих, гораздо меньше у человека, который волнуется и, следовательно, потеет и т. д.
- Серьёзные поражения тканей человека наблюдаются обычно при прохождении тока силой около 100 мА. Совершенно безопасным считается ток силой до 1 мА. Удельное сопротивление тела человека зависит от состояния кожных покровов. Сухая кожа обладает удельным сопротивлением порядка 10000 Ом·м, поэтому опасные токи могут быть достигнуты только при значительном напряжении. Однако при наличии сырости сопротивление тела человека резко снижается и безопасным может считаться напряжение только ниже 12 В. Удельное сопротивление крови 1 Ом·м при 50 Гц[7].
Метрологические аспекты[править | править код]
Приборы для измерения сопротивления[править | править код]
- Омметр
- Измерительный мост
- Амперметр и вольтметр (сопротивление находится по формуле)
Средства воспроизведения сопротивления[править | править код]
- Магазин сопротивлений — набор резисторов
- Катушки электрического сопротивления
Государственный эталон сопротивления[править | править код]
- ГЭТ 14-91 Государственный первичный эталон единицы электрического сопротивления. Институт-хранитель: ВНИИМ.
Статическое и динамическое сопротивление[править | править код]
В теории нелинейных цепей используются понятия статического и динамического сопротивлений. Статическим сопротивлением нелинейного элемента электрической цепи в заданной точке его ВАХ называют отношение напряжения на элементе к току в нем. Динамическим сопротивлением нелинейного элемента электрической цепи в заданной точке его ВАХ называют отношение бесконечно
малого приращения напряжения к соответствующему приращению тока.
См. также[править | править код]
- Сверхпроводимость
- Закон Ома
- Закон Барлоу
- Удельное электрическое сопротивление
- Электрическая проводимость
- Отрицательное сопротивление
- Внутреннее сопротивление
- Импеданс
- Волновое сопротивление
- Активное сопротивление
- Реактивное сопротивление
Примечания[править | править код]
Ссылки[править | править код]
- Таблица удельного сопротивления проводников
- Электрическое сопротивление проводников
Литература[править | править код]
- В. Г. Герасимов, Э. В. Кузнецов, О. В. Николаева. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.
Источник
Что такое сопротивление?
Сопротивление (электрическое сопротивление) – это свойство какого-либо проводника оказывать сопротивление электрическому току, проходящему через него. Вот так все просто!
Давайте проведем аналогию с гидравликой. В нашем случае получается, что проводник электрического тока – это шланг или труба. Теперь давайте подумаем, какой из предметов будет оказывать бОльшее сопротивление потоку воды: садовый шланг или нефтяная труба?


Понятное дело, что садовый шланг, так как его диаметр в разы меньше, чем диаметр нефтяной трубы.
Тогда другой вопрос. Какой шланг будет обладать бОльшим сопротивлением потоку воды с учетом того, что их длины и диаметры равны?


Разумеется, гофрированный. Вода будет “цепляться” за его стенки, что приведет к тому, что они будут мешать потоку воды.
Тогда еще вот такая задачка. Есть два абсолютно одинаковых шланга, но один длиннее, а другой короче. Какой из шлангов будет оказывать бОльшее сопротивление потоку воды?


Думаю тот, который длиннее. Ответ очевиден.
Сопротивление проводника
Так почему бы все эти свойства не применить также к проводнику? Чем тоньше и длиннее проводник, тем больше его сопротивление электрическому току. Большую роль играет также материал, из которого он изготовлен.
Поэтому, окончательная формула будет принимать вид
 формула сопротивления проводника
формула сопротивления проводника
В технике до сих пор применяется устаревшая единица измерения удельного сопротивления Ом × мм2 /м. Чтобы перевести в Ом × м, достаточно умножить на 10-6, так как 1 мм2=10-6 м2.
 удельное сопротивление веществ
удельное сопротивление веществ
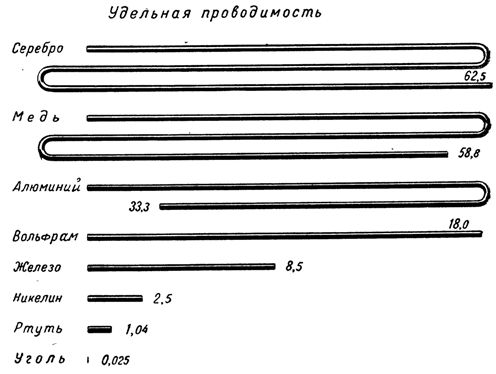
Как вы видите из таблицы выше, самым маленьким удельным сопротивлением обладает серебро, поэтому провод из серебра будет наилучшим проводником. Ну а самым распространенными и дешевыми проводниками являются медь и алюминий. Именно эти два металла в основном используются во всей электронной и электротехнической промышленности.
Вещества, которые оказывают наименьшее сопротивление электрическому току и обладают очень малым сопротивлением называются проводниками, а вещества, которые обладают ну очень большим сопротивлением электрическому току и почти его не пропускают через себя, называются диэлектриками. Между ними стоит класс полупроводников.
Что такое сопротивление 1 Ом?
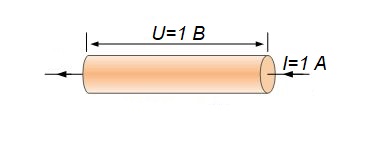
Проводник обладает сопротивлением 1 Ом, если на его концах напряжение составляет 1 Вольт при силе тока, проходящей через него в 1 Ампер.
 сопротивление 1 Ом
сопротивление 1 Ом
Это самое простое объяснение, что такое 1 Ом. В электротехнике и электронике сопротивление обозначается буквой R .
Как найти сопротивление в цепи?
Его можно узнать из закона Ома, который связывает силу тока, напряжение и сопротивление. В этом случае, оно рассчитывается по формуле
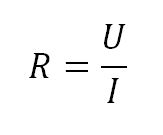 формула сопротивления через закон Ома
формула сопротивления через закон Ома
где
R – сопротивление, Ом
U – напряжение на концах проводника, Вольты
I – сила тока, текущая через проводник, Амперы
То есть нам достаточно замерить напряжение на концах какого-либо проводника и измерить силу тока, проходящую через него. После применить формулу и рассчитать сопротивление проводника. Давайте для закрепления решим простую задачу.
Задача
Рассчитать сопротивление проводника, если известно, что на него подают напряжение 5 Вольт и сила тока, проходящая через него 0,1 Ампер.
Решение
Используем формулу
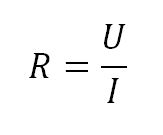

В электронике и электротехнике используют специальные радиоэлементы, которые обладают сопротивлением электрическому току – резисторы. Более подробно про них можно прочитать в этой статье.
постоянные резисторы
Также вот вам видео, где очень умный преподаватель объясняет, что такое сопротивление
Близкие темы к этой статье
Электрический проводник
Напряжение
Сила тока
Резисторы
Закон Ома
Входное и выходное сопротивление
Источник
Ïîíÿòèå îá ýëåêòðè÷åñêîì ñîïðîòèâëåíèè è ïðîâîäèìîñòè
Ëþáîå òåëî, ïî êîòîðîìó ïðîòåêàåò ýëåêòðè÷åñêèé òîê, îêàçûâàåò åìó îïðåäåëåííîå ñîïðîòèâëåíèå. Ñâîéñòâî ìàòåðèàëà ïðîâîäíèêà ïðåïÿòñòâîâàòü ïðîõîæäåíèþ ÷åðåç íåãî ýëåêòðè÷åñêîãî òîêà íàçûâàåòñÿ ýëåêòðè÷åñêèì ñîïðîòèâëåíèåì.
Ýëåêòðîííàÿ òåîðèÿ òàê îáúÿñíÿåò ñóùíîñòü ýëåêòðè÷åñêîãî ñîïðîòèâëåíèÿ ìåòàëëè÷åñêèõ ïðîâîäíèêîâ. Ñâîáîäíûå ýëåêòðîíû ïðè äâèæåíèè ïî ïðîâîäíèêó áåñ÷èñëåííîå êîëè÷åñòâî ðàç âñòðå÷àþò íà ñâîåì ïóòè àòîìû è äðóãèå ýëåêòðîíû è, âçàèìîäåéñòâóÿ ñ íèìè, íåèçáåæíî òåðÿþò ÷àñòü ñâîåé ýíåðãèè. Ýëåêòðîíû èñïûòûâàþò êàê áû ñîïðîòèâëåíèå ñâîåìó äâèæåíèþ. Ðàçëè÷íûå ìåòàëëè÷åñêèå ïðîâîäíèêè, èìåþùèå ðàçëè÷íîå àòîìíîå ñòðîåíèå, îêàçûâàþò ðàçëè÷íîå ñîïðîòèâëåíèå ýëåêòðè÷åñêîìó òîêó.
Òî÷íî òåì æå îáúÿñíÿåòñÿ ñîïðîòèâëåíèå æèäêèõ ïðîâîäíèêîâ è ãàçîâ ïðîõîæäåíèþ ýëåêòðè÷åñêîãî òîêà. Îäíàêî íå ñëåäóåò çàáûâàòü, ÷òî â ýòèõ âåùåñòâàõ íå ýëåêòðîíû, à çàðÿæåííûå ÷àñòèöû ìîëåêóë âñòðå÷àþò ñîïðîòèâëåíèå ïðè ñâîåì äâèæåíèè.
Ñîïðîòèâëåíèå îáîçíà÷àåòñÿ ëàòèíñêèìè áóêâàìè R èëè r.
Çà åäèíèöó ýëåêòðè÷åñêîãî ñîïðîòèâëåíèÿ ïðèíÿò îì.
Îì åñòü ñîïðîòèâëåíèå ñòîëáà ðòóòè âûñîòîé 106,3 ñì ñ ïîïåðå÷íûì ñå÷åíèåì 1 ìì2 ïðè òåìïåðàòóðå 0° Ñ.
Åñëè, íàïðèìåð, ýëåêòðè÷åñêîå ñîïðîòèâëåíèå ïðîâîäíèêà ñîñòàâëÿåò 4 îì, òî çàïèñûâàåòñÿ ýòî òàê: R = 4 îì èëè r = 4îì.
Äëÿ èçìåðåíèÿ ñîïðîòèâëåíèé áîëüøîé âåëè÷èíû ïðèíÿòà åäèíèöà, íàçûâàåìàÿ ìåãîìîì.
Îäèí ìåãîì ðàâåí îäíîìó ìèëëèîíó îì.
×åì áîëüøå ñîïðîòèâëåíèå ïðîâîäíèêà, òåì õóæå îí ïðîâîäèò ýëåêòðè÷åñêèé òîê, è, íàîáîðîò, ÷åì ìåíüøå ñîïðîòèâëåíèå ïðîâîäíèêà, òåì ëåã÷å ýëåêòðè÷åñêîìó òîêó ïðîéòè ÷åðåç ýòîò ïðîâîäíèê.
Ñëåäîâàòåëüíî, äëÿ õàðàêòåðèñòèêè ïðîâîäíèêà (ñ òî÷êè çðåíèÿ ïðîõîæäåíèÿ ÷åðåç íåãî ýëåêòðè÷åñêîãî òîêà) ìîæíî ðàññìàòðèâàòü íå òîëüêî åãî ñîïðîòèâëåíèå, íî è âåëè÷èíó, îáðàòíóþ ñîïðîòèâëåíèþ è íàçûâàåìóþ, ïðîâîäèìîñòüþ.

Ýëåêòðè÷åñêîé ïðîâîäèìîñòüþ íàçûâàåòñÿ ñïîñîáíîñòü ìàòåðèàëà ïðîïóñêàòü ÷åðåç ñåáÿ ýëåêòðè÷åñêèé òîê.
Òàê êàê ïðîâîäèìîñòü åñòü âåëè÷èíà, îáðàòíàÿ ñîïðîòèâëåíèþ, òî è âûðàæàåòñÿ îíà êàê 1/R,îáîçíà÷àåòñÿ ïðîâîäèìîñòü ëàòèíñêîé áóêâîé g.
Âëèÿíèå ìàòåðèàëà ïðîâîäíèêà, åãî ðàçìåðîâ è îêðóæàþùåé òåìïåðàòóðû íà âåëè÷èíó ýëåêòðè÷åñêîãî ñîïðîòèâëåíèÿ
Ñîïðîòèâëåíèå ðàçëè÷íûõ ïðîâîäíèêîâ çàâèñèò îò ìàòåðèàëà, èç êîòîðîãî îíè èçãîòîâëåíû. Äëÿ õàðàêòåðèñòèêè ýëåêòðè÷åñêîãî ñîïðîòèâëåíèÿ ðàçëè÷íûõ ìàòåðèàëîâ ââåäåíî ïîíÿòèå òàê íàçûâàåìîãî óäåëüíîãî ñîïðîòèâëåíèÿ.
 Óäåëüíûì ñîïðîòèâëåíèåì íàçûâàåòñÿ ñîïðîòèâëåíèå ïðîâîäíèêà äëèíîé 1 ì è ïëîùàäüþ ïîïåðå÷íîãî ñå÷åíèÿ 1 ìì2. Óäåëüíîå ñîïðîòèâëåíèå îáîçíà÷àåòñÿ áóêâîé ãðå÷åñêîãî àëôàâèòà ð. Êàæäûé ìàòåðèàë, èç êîòîðîãî èçãîòîâëÿåòñÿ ïðîâîäíèê, îáëàäàåò ñâîèì óäåëüíûì ñîïðîòèâëåíèåì.
Óäåëüíûì ñîïðîòèâëåíèåì íàçûâàåòñÿ ñîïðîòèâëåíèå ïðîâîäíèêà äëèíîé 1 ì è ïëîùàäüþ ïîïåðå÷íîãî ñå÷åíèÿ 1 ìì2. Óäåëüíîå ñîïðîòèâëåíèå îáîçíà÷àåòñÿ áóêâîé ãðå÷åñêîãî àëôàâèòà ð. Êàæäûé ìàòåðèàë, èç êîòîðîãî èçãîòîâëÿåòñÿ ïðîâîäíèê, îáëàäàåò ñâîèì óäåëüíûì ñîïðîòèâëåíèåì.
Íàïðèìåð, óäåëüíîå ñîïðîòèâëåíèå ìåäè ðàâíî 0,017, ò. å. ìåäíûé ïðîâîäíèê äëèíîé 1 ì è ñå÷åíèåì 1 ìì2 îáëàäàåò ñîïðîòèâëåíèåì 0,017 îì. Óäåëüíîå ñîïðîòèâëåíèå àëþìèíèÿ ðàâíî 0,03, óäåëüíîå ñîïðîòèâëåíèå æåëåçà – 0,12, óäåëüíîå ñîïðîòèâëåíèå êîíñòàíòàíà – 0,48, óäåëüíîå ñîïðîòèâëåíèå íèõðîìà – 1-1,1.
Ïîäðîáíåå îá ýòîì ÷èòàéòå çäåñü: ×òî òàêîå óäåëüíîå ýëåêòðè÷åñêîå ñîïðîòèâëåíèå
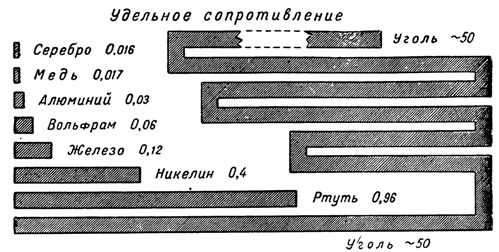
Ñîïðîòèâëåíèå ïðîâîäíèêà ïðÿìî ïðîïîðöèîíàëüíî åãî äëèíå, ò. å. ÷åì äëèííåå ïðîâîäíèê, òåì áîëüøå åãî ýëåêòðè÷åñêîå ñîïðîòèâëåíèå.
Ñîïðîòèâëåíèå ïðîâîäíèêà îáðàòíî ïðîïîðöèîíàëüíî ïëîùàäè åãî ïîïåðå÷íîãî ñå÷åíèÿ, ò. å. ÷åì òîëùå ïðîâîäíèê, òåì åãî ñîïðîòèâëåíèå ìåíüøå, è, íàîáîðîò, ÷åì òîíüøå ïðîâîäíèê, òåì åãî ñîïðîòèâëåíèå áîëüøå.
×òîáû ëó÷øå ïîíÿòü ýòó çàâèñèìîñòü, ïðåäñòàâüòå ñåáå äâå ïàðû ñîîáùàþùèõñÿ ñîñóäîâ, ïðè÷åì ó îäíîé ïàðû ñîñóäîâ ñîåäèíÿþùàÿ òðóáêà òîíêàÿ, à ó äðóãîé òîëñòàÿ. ßñíî, ÷òî ïðè çàïîëíåíèè âîäîé îäíîãî èç ñîñóäîâ (êàæäîé ïàðû) ïåðåõîä åå â äðóãîé ñîñóä ïî òîëñòîé òðóáêå ïðîèçîéäåò ãîðàçäî áûñòðåå, ÷åì ïî òîíêîé, ò. å. òîëñòàÿ òðóáêà îêàæåò ìåíüøåå ñîïðîòèâëåíèå òå÷åíèþ âîäû. Òî÷íî òàê æå è ýëåêòðè÷åñêîìó òîêó ëåã÷å ïðîéòè ïî òîëñòîìó ïðîâîäíèêó, ÷åì ïî òîíêîìó, ò. å. ïåðâûé îêàçûâàåò åìó ìåíüøåå ñîïðîòèâëåíèå, ÷åì âòîðîé.
Ýëåêòðè÷åñêîå ñîïðîòèâëåíèå ïðîâîäíèêà ðàâíî óäåëüíîìó ñîïðîòèâëåíèþ ìàòåðèàëà, èç êîòîðîãî ýòîò ïðîâîäíèê ñäåëàí, óìíîæåííîìó íà äëèíó ïðîâîäíèêà è äåëåííîìó íà ïëîùàäü ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ ïðîâîäíèêà:
R = p l / S,
ãäå – R – ñîïðîòèâëåíèå ïðîâîäíèêà, îì, l – äëèíà â ïðîâîäíèêà â ì, S – ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ ïðîâîäíèêà, ìì2.
Ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ êðóãëîãî ïðîâîäíèêà âû÷èñëÿåòñÿ ïî ôîðìóëå:
S = Ïè õ d2 / 4
ãäå Ïè – ïîñòîÿííàÿ âåëè÷èíà, ðàâíàÿ 3,14; d – äèàìåòð ïðîâîäíèêà.
À òàê îïðåäåëÿåòñÿ äëèíà ïðîâîäíèêà:
l = S R / p,
Ýòà ôîðìóëà äàåò âîçìîæíîñòü îïðåäåëèòü äëèíó ïðîâîäíèêà, åãî ñå÷åíèå è óäåëüíîå ñîïðîòèâëåíèå, åñëè èçâåñòíû îñòàëüíûå âåëè÷èíû, âõîäÿùèå â ôîðìóëó.
Åñëè æå íåîáõîäèìî îïðåäåëèòü ïëîùàäü ïîïåðå÷íîãî ñå÷åíèÿ ïðîâîäíèêà, òî ôîðìóëó ïðèâîäÿò ê ñëåäóþùåìó âèäó:
S = p l / R
Ïðåîáðàçóÿ òó æå ôîðìóëó è ðåøèâ ðàâåíñòâî îòíîñèòåëüíî ð, íàéäåì óäåëüíîå ñîïðîòèâëåíèå ïðîâîäíèêà:
ð = R S / l
Ïîñëåäíåé ôîðìóëîé ïðèõîäèòñÿ ïîëüçîâàòüñÿ â òåõ ñëó÷àÿõ, êîãäà èçâåñòíû ñîïðîòèâëåíèå è ðàçìåðû ïðîâîäíèêà, à åãî ìàòåðèàë íåèçâåñòåí è ê òîìó æå òðóäíî îïðåäåëèì ïî âíåøíåìó âèäó. Äëÿ ýòîãî íàäî îïðåäåëèòü óäåëüíîå ñîïðîòèâëåíèå ïðîâîäíèêà è, ïîëüçóÿñü òàáëèöåé, íàéòè ìàòåðèàë, îáëàäàþùèé òàêèì óäåëüíûì ñîïðîòèâëåíèåì.

Åùå îäíîé ïðè÷èíîé, âëèÿþùåé íà ñîïðîòèâëåíèå ïðîâîäíèêîâ, ÿâëÿåòñÿ òåìïåðàòóðà.
Óñòàíîâëåíî, ÷òî ñ ïîâûøåíèåì òåìïåðàòóðû ñîïðîòèâëåíèå ìåòàëëè÷åñêèõ ïðîâîäíèêîâ âîçðàñòàåò, à ñ ïîíèæåíèåì óìåíüøàåòñÿ. Ýòî óâåëè÷åíèå èëè óìåíüøåíèå ñîïðîòèâëåíèÿ äëÿ ïðîâîäíèêîâ èç ÷èñòûõ ìåòàëëîâ ïî÷òè îäèíàêîâî è â ñðåäíåì ðàâíî 0,4% íà 1°C. Ñîïðîòèâëåíèå æèäêèõ ïðîâîäíèêîâ è óãëÿ ñ óâåëè÷åíèåì òåìïåðàòóðû óìåíüøàåòñÿ.
 Ýëåêòðîííàÿ òåîðèÿ ñòðîåíèÿ âåùåñòâà äàåò ñëåäóþùåå îáúÿñíåíèå óâåëè÷åíèþ ñîïðîòèâëåíèÿ ìåòàëëè÷åñêèõ ïðîâîäíèêîâ ñ ïîâûøåíèåì òåìïåðàòóðû. Ïðè íàãðåâàíèè ïðîâîäíèê ïîëó÷àåò òåïëîâóþ ýíåðãèþ, êîòîðàÿ íåèçáåæíî ïåðåäàåòñÿ âñåì àòîìàì âåùåñòâà, â ðåçóëüòàòå ÷åãî âîçðàñòàåò èíòåíñèâíîñòü èõ äâèæåíèÿ. Âîçðîñøåå äâèæåíèå àòîìîâ ñîçäàåò áîëüøåå ñîïðîòèâëåíèå íàïðàâëåííîìó äâèæåíèþ ñâîáîäíûõ ýëåêòðîíîâ, îò÷åãî è âîçðàñòàåò ñîïðîòèâëåíèå ïðîâîäíèêà. Ñ ïîíèæåíèåì æå òåìïåðàòóðû ñîçäàþòñÿ ëó÷øèå óñëîâèÿ äëÿ íàïðàâëåííîãî äâèæåíèÿ ýëåêòðîíîâ, è ñîïðîòèâëåíèå ïðîâîäíèêà óìåíüøàåòñÿ. Ýòèì îáúÿñíÿåòñÿ èíòåðåñíîå ÿâëåíèå ñâåðõïðîâîäèìîñòü ìåòàëëîâ.
Ýëåêòðîííàÿ òåîðèÿ ñòðîåíèÿ âåùåñòâà äàåò ñëåäóþùåå îáúÿñíåíèå óâåëè÷åíèþ ñîïðîòèâëåíèÿ ìåòàëëè÷åñêèõ ïðîâîäíèêîâ ñ ïîâûøåíèåì òåìïåðàòóðû. Ïðè íàãðåâàíèè ïðîâîäíèê ïîëó÷àåò òåïëîâóþ ýíåðãèþ, êîòîðàÿ íåèçáåæíî ïåðåäàåòñÿ âñåì àòîìàì âåùåñòâà, â ðåçóëüòàòå ÷åãî âîçðàñòàåò èíòåíñèâíîñòü èõ äâèæåíèÿ. Âîçðîñøåå äâèæåíèå àòîìîâ ñîçäàåò áîëüøåå ñîïðîòèâëåíèå íàïðàâëåííîìó äâèæåíèþ ñâîáîäíûõ ýëåêòðîíîâ, îò÷åãî è âîçðàñòàåò ñîïðîòèâëåíèå ïðîâîäíèêà. Ñ ïîíèæåíèåì æå òåìïåðàòóðû ñîçäàþòñÿ ëó÷øèå óñëîâèÿ äëÿ íàïðàâëåííîãî äâèæåíèÿ ýëåêòðîíîâ, è ñîïðîòèâëåíèå ïðîâîäíèêà óìåíüøàåòñÿ. Ýòèì îáúÿñíÿåòñÿ èíòåðåñíîå ÿâëåíèå ñâåðõïðîâîäèìîñòü ìåòàëëîâ.
Ñâåðõïðîâîäèìîñòü, ò. å. óìåíüøåíèå ñîïðîòèâëåíèÿ ìåòàëëîâ äî íóëÿ, íàñòóïàåò ïðè îãðîìíîé îòðèöàòåëüíîé òåìïåðàòóðå -273° C, íàçûâàåìîé àáñîëþòíûì íóëåì. Ïðè òåìïåðàòóðå àáñîëþòíîãî íóëÿ àòîìû ìåòàëëà êàê áû çàñòûâàþò íà ìåñòå, ñîâåðøåííî íå ïðåïÿòñòâóÿ äâèæåíèþ ýëåêòðîíîâ.
Источник
