Какое свойство проводника характеризует его индуктивность

Воздушные катушки индуктивности с различными рабочими характеристиками

К сведению. Следует учитывать тот факт, что при рассмотрении высокочастотного диапазона влияние индуктивности значительно даже при работе с прямыми участками проводников.

К сведению. На основе приведенных рассуждений можно сделать промежуточный вывод о минимальном значении формы контура (при работе с низкими и средними частотами).

Значение индуктивности зависит от магнитных параметров материала сердечника

Важно! В реальных условиях структура магнитных полей значительно отличается в центральной части и на краях катушки.

Таблица с формулами для расчета самоиндукции типовых замкнутых контуров

К сведению. Катушку какой индуктивности надо включить для решения определенной задачи, вычисляют с помощью рассмотренных выше формул.

Взаимоиндукция

в электродинамике (коэффициент самоиндукции) (от лат. inductio – наведение, побуждение) – параметр электрич. цепи, определяющий величину эдс самоиндукции, наводимой в цепи при изменении протекающего по ней тока и (или) при её деформации. Термин “И.” употребляется также для обозначения элемента цени (двухполюсника), определяющего её индуктивные свойства (синоним – катушка самоиндукции).И. является количеств. характеристикой эффекта самоиндукции, открытого независимо Дж. Генри (J. Henry) в 1832 и М. Фарадеем (М. Faraday) в 1835. При изменении тока в цепи и (или) при её деформации происходит изменение магн. поля, к-рое, в соответствии с законом индукции, приводит к возникновениювихревого электрич. поля E(r, t )с отличной от нуля циркуляцией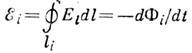

по замкнутым контурам li;пронизываемым магн. потоком Ф i. Внутри проводника вихревое поле Е взаимодействует с порождающим его током и оказывает противодействие изменению магн. потока (Ленца правило). Циркуляция Ei и магн. поток Ф i существенно зависят от выбора контура li внутри проводника конечной толщины. Однако при медленных движениях и квазистацнонарных процессах, когда полный ток

(j – плотностьтока) одинаков для всех нормальных сечений провода S пр, допустим переход к усреднённым характеристикам: эдс самоиндукции E си=<Ei> )и сцепленному с проводящим контуром магн. потоку Ф=<Ф i>. В предположении о том, что линии тока замыкаются сами на себя при одном обходе по контуру,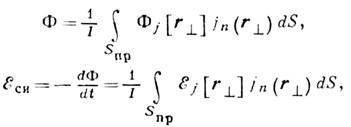

где r^ , – радиус-векторы точек нормального сечения провода, Ф j(r^) – магн. поток через поверхность, ограниченную линией тока, проходящей через точку r^, Ej(r^) – циркуляция вектора E вдоль этой линии тока, jn – нормальная к Snp составляющая j. В более сложных ситуациях, когда линии тока замыкаются после неск. обходов по контуру или вообще не являются замкнутыми кривыми, процедура усреднения требует уточнений, однако во всех случаях она должнаудовлетворять энергетич. соотношению: 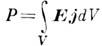=E сиI ( Р– суммарная мощность взаимодействия поля с током).Усреднённый магн. поток в случае квазистацнонарных процессов пропорц. току:

Ф=L.I (в СИ), Ф=1/c(LI)(в системе СГС). (1)

Коэф. L и Lназ. И. Величина L измеряется в генри, L – в см.

E си=-d/dt(LI) (в СИ), Ecи=-(1/с 2)(d/dt)(LI)(2) (в системе СГС).

Производная по времени от И. определяет ту часть E си, к-рая связана с деформацией проводящего контура; в случае недеформируемых цепей и квазистационарных процессов И. может быть вынесена из-под знака дифференцирования. энергия, запасённая в создаваемом им магн. поле, записывается в форме, аналогичной выражению для кинетич. энергии.

Wm=1/2LI2 (в СИ), Wm=1/2c2LI2 (в системе СГС). (3)

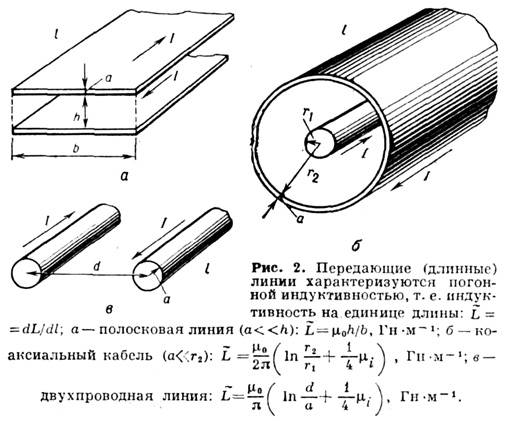
Соотношение (3) позволяет различать И. внутреннюю Li, определяющую энергию магн. поля, сосредоточенного в проводниках, и внешнюю Le, связанную с внеш. магн. полем (L=Li+Le, L=Li+Le). В важном частном случае токовой цепи, выполненной из проводов, толщина к-рых мала по сравнению с радиусамиих изгибов или расстояниями между соседними проводами, можно считать, что структура токов и ближнего магн. поля такая же, как и для прямого провода того же сечения (подобные проводники наз. квазилинейными). В приближении заданной структуры токов, не зависящей от способа их возбуждения, И. определяется только геометрией проводящей цепи (толщиной и длиной проводов и их формой). Для квазилинейного провода кругового сечения Li=(m0/8p)mil (l – длина провода, mi – магн. проницаемость проводника), а внешняя И. может быть представлена как индуктивность взаимная двух параллельных бесконечно тонких проводящих нитей, одна из к-рых (l1) совпадает с осевой линией проводника, а другая (l2) совмещена с его поверхностью: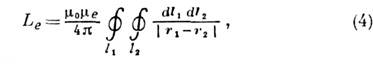

где r1, r2 – радиус-векторы точек на контурах ll,l2,m е – магн. проницаемость окружающей среды [для аналогия, соотношений в системе СГС L “(m0/4p)L]. Из (4) видно, что Le логарифмически расходится при стремлении радиуса провода к нулю, поэтому идеализацией бесконечно тонкого провода нельзя пользоваться при описании явлений самоиндукции. Приближённые вычисления интеграла в (4) с учётом внутренней И. дают:

где l и а – длина и радиус провода. Это выражение обладает логарифмич. точностью – его относит. погрешность порядка величины l/ln(l/a). Примеры типичных электрич. цепей и выражения для их И. приведены на рис. 1 и 2.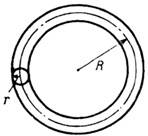

Рис. 1. Круговой виток. Индуктивность витка (проводящего тора): L=m0R(ln(8R/r)-2+1/4mi), Гн, r<<R.

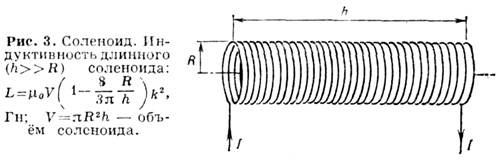
Особое значение в электротехнике и радиотехнике имеют проволочные катушки с достаточно плотной намоткой – соленоиды (рис. 3), применяемые для увеличения И. Поскольку И. цепей, в к-рые включены соленоиды, ими в основном и определяются, принято говорить об И. соленоида. Под величиной И. идеальногосоленоида понимают И. эфф. проводящей поверхности (совпадающей с его каркасом), по к-рой протекают азимутальные поверхностные токи с плотностью j пов=Ik (I – ток в соленоиде, k – число витков на единице длины).

Понятие И. допускает обобщение на быстропеременные гармонич. ехр(iwt)-процессы, при описании к-рых нельзя пренебрегать запаздыванием эл.-магп. взаимодействий, скин-эффектом в проводниках, дисперсией среды. Комплексные амплитуды тока Iw и эдс самоиндукции Ew связаны соотношением:

И. L(w) зависит от частоты (как правило, уменьшается с её ростом). Эфф. сопротивление RL(w) определяет часть энергетич. потерь, в т. ч. потери на излучение, и связано с L(w) Крамерса – Кронига соотношением: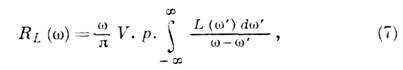

где интеграл берётся в смысле гл. значения. На низких частотах сопротивлением RL(w) можно пренебречь, тогда Ew и Iw сдвинуты по фазе на p/2. Соотношение (3) для высокочастотных процессов преобразуется к виду: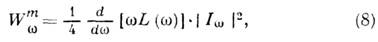

где Wmw– усреднённая по периоду колебаний энергия ближних (квазистационарных) магн. полей (полная магн. энергия поля не определена из-за линейно растущей во времени энергии поля излучения).Если в цепи действует гармонич. сторонняя эдс 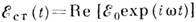, то во втором законе Кирхгофа величина Ew может быть перенесена (со сменой знака) в правую часть равенства: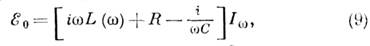

где С –ёмкость, включённая в цепь. Соотношение (9) позволяет трактовать величину ZL=iwLкак индуктивную часть импеданса цепи (при атом ZC=-i/w С –ёмкостная, a ZR=R– активная части полного импеданса Z=ZL+ZC+ZR). Принято считать, что импеданс двухполюсника имеет индуктивный характер, если его мнимая часть больше нуля [если рассматриваются ехр (-iwt)-процессы, то меньше нуля]. В технике довольно часто И. наз. любой двухполюсник, импеданс к-рого имеет индуктивный характер п в опредсл. диапазоне частот линейно зависит от w. Если индуктивные элементы выполнены в виде катушек самоиндукции, то считать их двухполюсниками можно, вообще говоря, только в том случае, когда взаимодействие через магн. поля между ними и с др. элементами цепи пренебрежимо мало. Тогда их импедансы можно складывать в соответствии с правилами Кирхгофа: при последовательном соединении 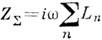, а при параллельном 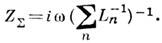При описании сильноточных цепей часто требуется обобщение понятия И. на случай нелинейных систем. Если неподвижный проводящий контур помещён всреду, в к-рой вектор магн. индукции В и напряжённость магн. поля Н связаны нелинейным локальным соотношением: B(r, t)=B[H(r, t)], то сцепленный с контуром магн. поток можно считать однозначной ф-цией тока Ф=Ф(I). В соответствии с законом индукции Фарадея, эдс самоиндукции в контуре равна: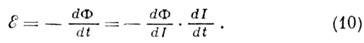

Величина L Д(I)=d Ф /dIназ. дифференциальной (или иногда динамической) И. Выражение для запасённой энергии пост. тока приобретает вид: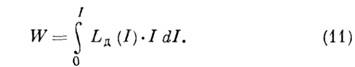

B линейном приближении (при I “0) L Д “L и выражения (10), (11) переходят в (2) и (3) соответственно. Лит.: Тамм И. Е., Основы теории электричества9 изд., М., 1976; Калантаров П. Л., Цейтлин Л. А. Расчет индуктивностей, 3 изд., Л., 1986; Ландау Л. Д. Лифшиц Е. М., Электродинамика сплошных сред, 2 изд. М., 1982. М. А. Миллер, Г. В. Пермитин

Индуктивность — это физическая величина, характеризующая магнитные свойства электрической цепи. В некоторых источниках её называют коэффициентом самоиндукции, так как она зависит от текущего в замкнутом контуре тока и создаваемого им магнитного потока. Для определения величины этого показателя применяют несколько вариантов расчёта, которые основываются на различных физических параметрах.

Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

1. Величина параметра никогда не может быть меньше нуля.
2. Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

Способы расчёта

Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.

Через силу тока

Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:

• L — индуктивность контура (в генри);
• Ф — величина магнитного потока, измеряемого в веберах;
• I — сила тока в катушке (в амперах).

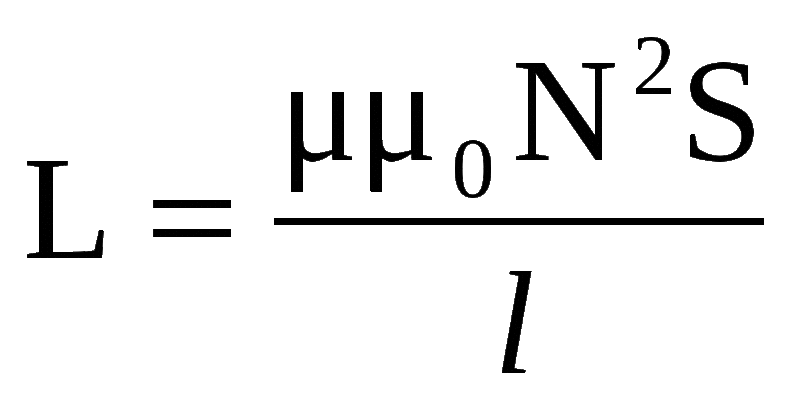
Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.

Соленоид конечной длины

Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:

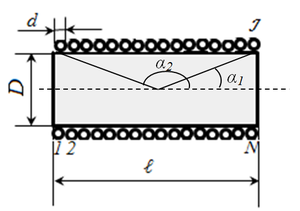• µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
• N — количество витков в катушке;
• S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
• l — длина соленоида в метрах.

Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:

• W — энергия магнитного потока, измеряемая в джоулях;
• I — сила тока в амперах.

Катушка с тороидальным сердечником

В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:

• N — число витков катушки;
• µ — относительная магнитная проницаемость;
• µ0 — магнитная постоянная;
• S — площадь сечения сердечника;
• π — математическая постоянная, равная 3,14;
• r — средний радиус тора.

Длинный проводник

Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:

• l — длина проводника в метрах;
• r — радиус сечения провода, измеряемый в метрах;
• µ0 — магнитная постоянная;
• µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
• µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
• π — число Пи;
• ln — обозначение логарифма.

Варианты измерения

Индуктивность катушки в физике определяется путём выполнения вычислений. Однако эту величину можно не только рассчитать, но и измерить. Делается это при помощи прямого или косвенного метода.

Прямой метод

Для измерения индуктивности катушки этим методом необходимо использовать специальные мостовые или прямопоказывающие устройства. С их помощью можно получить максимально точные данные, которые помогут выбрать требуемую катушку для схемы.

Порядок проведения измерений включает в себя следующие этапы:

1. К прямопоказывающему приспособлению подключают катушку.
2. После этого постепенно изменяют диапазоны измерений. Это делается до тех пор, пока получаемый результат не будет находиться примерно в середине интервала.
3. Полученный результат фиксируют и высчитывают с учётом цены деления прибора, а также коэффициента, соответствующего положению переключателя.

Прямой метод измерения можно применить и при определении индуктивности с помощью мостового приспособления. Оно имеет более точную шкалу, поэтому позволяет получить достоверные данные.

Измерение выполняют путём проведения таких действий:

1. Включённый мостовой прибор подсоединяют к катушке, индуктивность которой необходимо определить.
2. Аналогично прямопоказывающему устройству проводят переключение интервалов измерений.
3. После каждого такого действия ручку регулятора балансировки моста поочерёдно перемещают в одно и другое предельное положение.
4. Как только удалось определить диапазон, в котором мост будет сбалансирован, можно выполнять дальнейшие действия.
5. На следующем этапе измерений выполняется постепенное перемещение стрелочного индикатора.
6. После того как в динамике прибора исчезнет звук, необходимо зафиксировать показатели.
7. Затем их рассчитывают в соответствии с ценой деления шкалы и предусмотренным коэффициентом.

Косвенное определение

Для того чтобы измерить коэффициент самоиндукции, необходимо провести несколько подготовительных мероприятий. В первую очередь нужно собрать измерительную цепь по стандартной схеме, а также подготовить все необходимые приспособления (генератор синусоидального напряжения, частотомер, а также миллиамперметр и вольтметр, рассчитанные на переменный ток).

Порядок определения параметра:

1. К выходу генератора параллельно подключают вольтметр. Он должен быть переключён в режим, при котором верхнее предельное значение будет соответствовать напряжению в 3−5 вольт.
2. Аналогично подсоединяют и частотомер.
3. Отдельно собирают вторую цепь. В ней последовательно соединяют миллиамперметр и катушку, индуктивность которой нужно определить.
4. Затем обе цепи подключают параллельно друг к другу.
5. Подключённый генератор устанавливают в режим выработки синусоидального напряжения.
6. Путём изменения частоты добиваются такой работы приборов, при которой вольтметр будет показывать примерно 2 вольта. При этом сила тока на миллиамперметре будет постепенно уменьшаться.
7. После этого ручку частотомера перемещают в положение, соответствующее частоте измерений.
8. Как только эти действия будут выполнены, можно фиксировать значения.

Полученные данные переводятся в СИ, а затем выполняются все необходимые расчёты. Первым делом определяется индуктивное сопротивление. Для этого значения приборов подставляются в следующую зависимость: X=U/I, где U — напряжение, а I — сила тока. Результат расчётов будет выражен в омах.

После этого вычисляется индуктивность по формуле L=X/2 πF. В ней используются такие условные обозначения:

• X — индуктивное сопротивление;
• π — математическая постоянная (примерно 3,14);
• F — частота в герцах, при которой проводились измерения.

Индуктивность — это важный физический параметр, позволяющий определить магнитные свойства электроцепи. При точном его измерении и правильном проведении предусмотренных расчётов можно получить достоверные данные, которые понадобятся при выборе катушки.