Какое свойство не является свойством алгоритма
1) дискретность
2) массовость
3) результативность
4) цикличность
Задание 41
Не является свойством алгоритма
1)дискретность 2) понятность 3)дистрибутивность 4) результативность
Очевидно, что оба эти задания из-за особенностей содержания не могут быть расположены в одном тесте. Они интересны тем, что имеют одинаковые содержательные основы и частично пересекающиеся множества ответов. При выполнении задания 40 знающий ученик выберет правильный ответ, отметив попутно для себя, что два ответа принадлежат обоим заданиям теста. Поэтому при выполнении задания 41 ученик будет выбирать уже не из четырех, а только из двух ответов.
Еще меньше оснований для размещения в одном тесте, к примеру, двух таких заданий:
Задание 42
О каком городе писал Пушкин в стихах «Люблю тебя, Петра творенье, Люблю твой строгий, стройный вид, Невы державное теченье, Береговой ее гранит…»
а) Москва
б) Тверь
в) Санкт-Петербург
Задание 43
Многие русские поэты писали о Санкт-Петербурге. Кому принад лежат строки
«Люблю тебя, Петра творенье,
Люблю твой строгий, стройный вид,
Невы державное теченье,
Береговой ее гранит…»
а) Пастернак
б) Пушкин
в) Ахматова
г) Есенин
Вполне очевидно, что правильный ответ на последнее задание вытекает из предыдущего, содержащего явную подсказку. Возможно, многим покажется, что приведенные примеры несколько утрируют ситуацию. Однако это сделано не случайно, а из дидактических соображений, чтобы яснее стали ошибки, допускаемые авторами в процессе разработки теста. Конечно, каждое из заданий 42 и 43 само по себе достаточно удачно, но размещать их следует не в одном, а в разных вариантах теста.
Фасетные задания в тесте
Идея много вариантности близка и понятна любому педагогу. Даже в условиях хорошо организованного процесса применения
тестов один вариант даст смещение оценки учеников из-за списывания, подсказок и других подобных нежелательных эффектов. К тому же единственный вариант легко рассекречивается. Как только тест выдается классу, часть правильных ответов становится известной ученикам, и потому задания приходится менять при очередном использовании теста. Одним из методов преодоления отмеченных проблем является разработка фасетных заданий. В ряде зарубежных работ под фасетом понимается форма, обеспечивающая представление нескольких вариантов одного и того же элемента содержания теста [51,53].
Фасетные задания можно использовать как в закрытой, так и в открытой форме. Каждый испытуемый получает из фасета только один вариант задания. При этом все испытуемые группы выполняют однотипные задания, но с разными элементами фасета и соответственно с разными ответами. Таким образом решаются одновременно две задачи: устраняется возможность списывания и обеспечивается параллельность вариантов тестов, предлагаемых различным ученикам. Например, в приведенном далее фасетном задании
Задание 44
К дворцовым комплексам окрестностей
[Москвы ]
[Санкт-Петербурга]
от носятся
1) Павловск, Ораниенбаум
2) Архангельское, Царицыно
3) Петергоф, Гатчина
4)Царское село, Стрельна
содержатся два варианта:
Задание 45
К дворцовым комплексам окрестностей Москвы относятся
1) Павловск, Ораниенбаум
2)Архангельское, Царицыно
3) Петергоф, Гатчина
4) Царское село, Стрельна
Задание 46
К дворцовым комплексам окрестностей Санкт-Петербурга относятся
1) Павловск, Ораниенбаум
2) Архангельское, Царицыно
3) Петергоф, Гатчина ,
4) Царское село, Стрельна
В других фасетных заданиях заложена возможность получения целого ряда «параллельных» по содержанию и по форме заданий теста.
Задание 47
Автор знаменитых картин
(Явление Христа народу)
( Демон)
а) Репин б) Рублев в) Иванов г) Врубель
Задание 48
[Баженова]
По проекту архитектора (……….) был построен.
1) дом Пашкова в Москве
2) Московский университет
3) Зимний дворец в Петербурге
4)Собор Петропавловской крепости
Особенно легко и удобно создавать фасетные задания по естественному циклу дисциплин путем введения параметров в задания теста. Например, если нужно проверить умение решать квадратные уравнения, то, выбирая различные значения параметров — коэффициентов уравнения, можно получить множество вариантов фасета. Например, выбирая различные значения параметров а, Ь, с, обеспечивающие не отрицательность дискриминанта квадратного уравнения в задании,
Задание 49
Корни квадратного уравнения {а}х2 + { b }х + {с} = О принадлежат интервалу
1)… 2)… 3)…
и добавляя соответствующие ответы, можно разработать множество заданий для различных вариантов теста.
При этом все ученики выполняют однотипные задания, но с различными коэффициентами, что отчасти устраняет возможность списывания, подсказки и других нарушений.
Одному ученику попадается уравнение х2+2х-3 = 0(а=1, b = = 2, с=-3), другому х2 + 5х + 6 = 0 и т. д. Однако и здесь есть определенные осложнения, так как такого рода уравнения могут быть далеко не равноценными по трудности, поскольку гораздо удобнее делать вычисления при малых значениях коэффициентов, чем при больших. Поэтому говорить о полном устранении всех проблем разработки многовариантных тестов с помощью фасета, конечно, нельзя. Многие осложнения вполне преодолимы благодаря специальным методам, разрабатываемым для выравнивания результатов выполнения параллельных вариантов теста [47].
коррекция тестовых баллов с поправкой на догадку (задания с четырьмя и пятью ответами)
Формула коррекции на возможную догадку для индивидуальных баллов, полученных в результате выполнения заданий с четырьмя ответами, из которых один верный, имеет вид [43]
где все обозначения прежние.
Для рассмотренного ранее примера выполнения заданий с тремя ответами Xf = 50 и Vt = 10. Скорректированный балл, полученный учеником при правильном выполнении 50 из 60 заданий теста с четырьмя ответами, будет
или округленно 47 баллов. Сопоставление с результатами коррекции для случая заданий с двумя и тремя ответами показывает, что испытуемому засчитывается 47 баллов из 50 правильных ответов, в то время как ранее засчитывалось 40 баллов (задание с двумя ответами) и 45 баллов (с тремя).
Для заданий с пятью ответами коррекция будет еще меньше. В этом случае
а для рассматриваемого примера
Xi = 50 –10/4= 50-2,5 = 48 баллов
48 баллов.
Таким образом, с увеличением количества дистракторов к заданию число вычитаемых баллов уменьшается, что вполне естественно, так как чем больше дистракторов, тем труднее угадать правильный ответ. Следовательно, в заданиях с большим количеством дистракторов на первый план при выборе правильного ответа выходят знания, а не догадка.
В целом же можно отметить, что формула коррекции индивидуальных баллов имеет довольно ограниченную сферу применения. Это связано с теми дополнительными трудностями, которые привносятся в процесс обработки скорректированных результатов тестирования, когда они после коррекции переносятся на область отрицательных и дробных чисел.
Действительно, если учащийся выполнил лишь незначительное количество заданий, то после коррекции его балл может стать отрицательным числом. Например, если Xi = 10, а всего в тесте 60 заданий с 5 ответами, то после коррекции
X ‘ i =10-50/4 = 10-12,5 = -2,5.
В этом случае приходится применять дополнительные преобразования скорректированных баллов, чтобы перевести их на область положительных целых чисел.
Правда, как уже отмечалось ранее, коррекция нужна не всегда. Если в инструкции для испытуемых содержалось требование не угадывать ответы к заданиям и переходить в случае затруднений к выполнению других заданий теста, то эффектом угадывания можно пренебречь. Хотя следует помнить, что далеко не все ученики при затруднениях поступят согласно требованиям инструкции, поэтому без коррекции результаты отдельных слабых учащихся будут явно завышены.
Дата добавления: 2018-10-14; просмотров: 1715 | Нарушение авторских прав | Изречения для студентов
Читайте также:
Рекомендуемый контект:
Поиск на сайте:
© 2015-2020 lektsii.org – Контакты – Последнее добавление
Источник
Valera
Высший разум
(218914)
8 лет назад
Свойства алгоритма
Алгоритм обладает следующими свойствами:
1. Дискретность. Это свойство состоит в том, что алгоритм должен представлять процесс решения задачи как последовательное выполнение простых шагов. При этом для выполнения каждого шага алгоритма требуется конечный отрезок времени, т. е. преобразование исходных данных в результат осуществляется во времени дискретно.
2. Определенность. Каждое правило алгоритма должно быть четким, однозначным.
3. Результативность. Алгоритм должен приводить к решению за конечное число шагов.
4. Массовость. Алгоритм решения задачи разрабатывается в общем виде, т. е. он должен быть применим для некоторого класса задач, различающихся лишь исходными данными.
5. Правильность. Алгоритм правильный, если его выполнение дает правильные результаты решения поставленной задачи.
SerGo
Высший разум
(101320)
8 лет назад
• Дискретность (прерывность, раздельность) – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.
• Определенность – каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
• Понятность алгоритма – алгоритм, составленный для конкретного исполнителя, должен включать только те команды, которые входят в его систему команд.
• Результативность (конечность) – алгоритм должен приводить к решению задачи за конечное число шагов.
• Массовость – алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.
Свойства алгоритма
Евгенний Парфенюк
Ученик
(153)
4 месяца назад
Дискретность (прерывность, раздельность) – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.
• Определенность – каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
• Понятность алгоритма – алгоритм, составленный для конкретного исполнителя, должен включать только те команды, которые входят в его систему команд.
• Результативность (конечность) – алгоритм должен приводить к решению задачи за конечное число шагов.
• Массовость – алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.
Источник
Алгоритм. Свойства алгоритмов.
Блок-схемы. Алгоритмические языки
Код ОГЭ: 1.3.1. Алгоритм, свойства алгоритмов, способы записи алгоритмов.
Блок-схемы. Представление о программировании
Понятие алгоритма является одним из основных понятий вычислительной математики и информатики.
■ Алгоритм
— строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов.
Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя.
Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.

В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные.
Свойства алгоритмов
Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:
- Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
- Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
- Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
- Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
- Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.
Способы представления алгоритмов:
- словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
- блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
- формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
- псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.
Словесная запись алгоритма
Произвольное изложение этапов алгоритма на естественном языке имеет свои недостатки. Словесные описания строго не формализуемы, поэтому может быть нарушено свойство определенности алгоритма: исполнитель может неточно понять описание этапа алгоритма. Словесная запись достаточно многословна. Сложные задачи трудно представить в словесной форме.
■ Пример 1. Записать в словесной форме правило деления обыкновенных дробей.
Решение.
Шаг 1. Числитель первой дроби умножить на знаменатель второй дроби.
Шаг 2. Знаменатель первой дроби умножить на числитель второй дроби.
Шаг 3. Записать дробь, числителем которой являет результат выполнения шага 1, знаменателем — результат выполнения шага 2.
Описанный алгоритм применим к любым двум обыкновенным дробям. В результате его выполнения будут получены выходные данные — результат деления двух дробей (исходных данных).
Формальные исполнители алгоритма
Формальный исполнитель — это исполнитель, который выполняет все команды алгоритма строго в предписанной последовательности, не вникая в его смысл, не внося ничего в алгоритм и ничего не отбрасывая. Обычно под формальным исполнителем понимают технические устройства, автоматы, роботов и т. п. Компьютер можно считать формальным исполнителем.
Программы на языке произвольного формального исполнителя могут состоять только из элементарных команд, которые входят в его систему (которые исполнитель «понимает»).
Исполнитель может иметь свою среду (например, систему координат, клеточное поле и др.). Среда исполнителя — это совокупность объектов, над которыми он может выполнять определенные действия (команды), и связей между этими объектами. Алгоритмы в этой среде выполняются исполнителем по шагам.
■ Пример 2. Исполнитель Крот имеет следующую систему команд:
- вперед k — продвижение на указанное число шагов вперед;
- поворот s — поворот на s градусов по часовой стрелке;
- повторить m [команда1 … командаN] — повторить m раз серию указанных команд.
Какой след оставит за собой исполнитель после выполнения следующей последовательности команд?
Повторить 5 [вперед 10 поворот 72]
Решение. Команда вынуждает исполнителя 5 раз повторить набор действий: пройти 10 шагов вперед и повернуть на 72° по часовой стрелке. Так как поворот происходит на один и тот же угол, то за весь путь исполнитель повернет на 5 х 72° = 360°. Поскольку все отрезки пути одинаковой длины и сумма внешних углов любого многоугольника составляет 360°, то в результате будет оставлен след в форме правильного пятиугольника со стороной в 10 шагов исполнителя.
Заметим, что если увеличить количество повторов серии команд, то исполнитель будет повторно передвигаться по тем же отрезкам (произойдет повторное движение по тому же пятиугольнику).
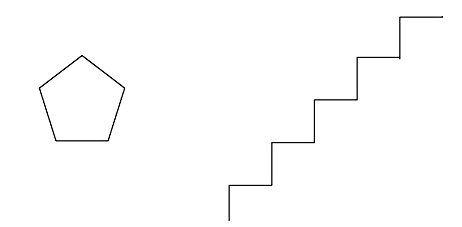
■ Пример 3. В системе команд предыдущего исполнителя Крот сформировать алгоритм вычерчивания пятиступенчатой лестницы (длина ступеньки — 10 шагов исполнителя).
Решение. За каждый шаг цикла должно происходить 4 действия: движение вперед на 10 шагов исполнителя, поворот на 90° по часовой стрелке, еще 10 шагов вперед и поворот на 90° против часовой стрелки (= 270° по часовой). В результате за один шаг цикла формируется ломаная из двух отрезков длиной 10 под прямым углом. За пять таких шагов сформируется 5–ступенчатая лестница (ломаная будет содержать 10 звеньев).
Повторить 5 [вперед 10 поворот 90 вперед 10 поворот 270]
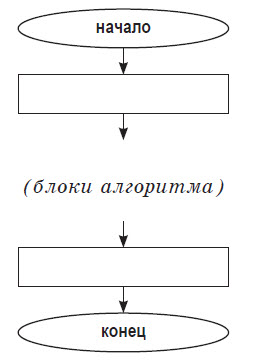
Блок–схема
Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока. Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).
Основные элементы блок–схемы алгоритма:

Общий вид блок–схемы алгоритма:

■ Пример 4. Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.
Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.
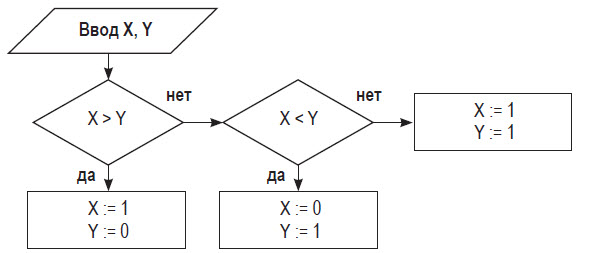
Решение.
- Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
- В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 < 12), происходит переход по линии «нет».
- Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да».
- Вычисляется результат выполнения алгоритма: X := 0, Y := 1.
Ответ: X := 0, Y := 1.
Алгоритмические языки
Алгоритмический язык — это искусственный язык (система обозначений), предназначенный для записи алгоритмов. Он позволяет представить алгоритм в виде текста, составленного по определенным правилам с использованием специальных служебных слов. Количество таких слов ограничено. Каждое служебное слово имеет точно определенный смысл, назначение и способ применения. При записи алгоритма служебные слова выделяют полужирным шрифтом или подчеркиванием.
В алгоритмическом языке используются формальные конструкции, но нет строгих синтаксических правил для записи команд. Различные алгоритмические языки различаются набором служебных слов и формой записи основных конструкций.
Алгоритмический язык, конструкции которого однозначно преобразуются в команды для компьютера, называется языком программирования. Текст алгоритма, записанный на языке программирования, называется программой.
Псевдокод
Псевдокод занимает промежуточное положение между естественным языком и языками программирования. Пример псевдокода — учебный алгоритмический язык. Алфавит учебного алгоритмического языка является открытым. Существенным достоинством этого языка является то, что его служебные слова, конструкции и правила записи алгоритма весьма схожи с теми, что применяются в распространенных языках программирования. Благодаря этому учебный алгоритмический язык позволяет легче освоить основы программирования.
Служебные слова учебного алгоритмического языка:
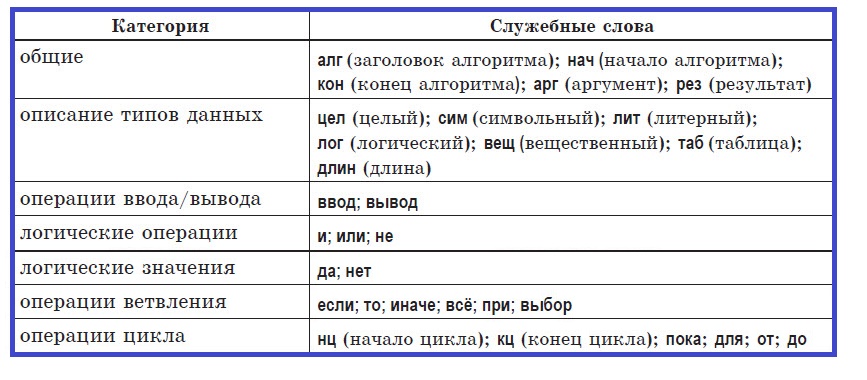
Стандартная структура алгоритма
Представление алгоритма на алгоритмическом языке (в том числе и языке программирования) состоит из двух частей. Первая часть — заголовок — задает название алгоритма и включает описание переменных, которые используются в нем. Вторая часть — тело алгоритма — содержит последовательность команд алгоритма.
Общий вид записи алгоритма на учебном алгоритмическом языке:

В начале заголовка записывается служебное слово алг, после чего указывается имя алгоритма. Описание переменных, являющихся аргументами алгоритма и его результатами, приводится после названия в круглых скобках.
В следующих строках конкретизируют, какие именно переменные являются аргументами алгоритма (входными данными), а какие — его результатами (выходными данными). Для этого после служебного слова арг приводится список имен переменных–аргументов; в следующей строке после служебного слова рез приводится список имен переменных–результатов.
Между служебными словами нач и кон размещается тело алгоритма — конечная последовательность команд, выполнение которых предписывает алгоритм. Команды алгоритма записывают одну за одной в отдельных строках. В случае необходимости можно записать две или более команд в одной строке, тогда соседние команды разделяют точкой с запятой. Если в алгоритме применяются промежуточные переменные, их описание приводят в начальной строке тела алгоритма рядом со словом нач.
Примеры заголовков алгоритмов:

В первом примере алгоритм имеет название Объем_шара, один вещественный аргумент Радиус и один вещественный результат Объем. Во втором примере алгоритм под названием Choice имеет три аргумента — целые M и N и логический b, а также два результата — вещественные Var1 и Var2.
Пример алгоритма вычисления гипотенузы прямоугольного треугольника:

На вход алгоритму даются два вещественных аргумента a и b (величины катетов), результатом является вещественная переменная с (гипотенуза). Для ее расчета используется функция вычисления квадратного корня sqrt.
Описание величин и действия над ними
При описании алгоритма необходимо указать названия (обозначения) всех величин, которые будут в нем найдены или использованы.
При представлении алгоритма решения в виде блок–схемы выбранные обозначения величин приводятся отдельно от блок–схемы (как объяснение к ней). Если алгоритм представлен на языке программирования, то характеристика обрабатываемых величин включается в программу. Учебный алгоритмический язык также предусматривает описание величин, используемых в алгоритме.
Все величины в алгоритме разделяют на постоянные (константы) и переменные. Константа не может изменять свои значения в процессе работы алгоритма. Переменная может приобретать различные значения, которые сохраняются до тех пор, пока она не получит новое значение. Переменным величинам назначают имена. Таким образом, переменная — это именуемая величина, которая в процессе выполнения алгоритма может приобретать и хранить различные значения.
В алгоритмическом языке не существует специальных правил именования переменных. Однако их названия не должны совпадать со служебными словами алгоритмического языка. Во многих языках программирования для имен можно использовать только латинские буквы, цифры, знак подчеркивания. Имена обязательно должны начинаться с буквы, при этом строчные и прописные буквы в именах не различаются. В одном алгоритме не могут существовать разные объекты с одинаковыми именами. Все имена являются уникальными. Имена переменных и констант стараются выбирать так, чтобы они напоминали их смысл. Например, имена переменных и констант: S, p12, result, итог.
При представлении алгоритма на алгоритмическом языке именуются не только величины, но и сам алгоритм, и другие объекты. Имя алгоритма выбирают так же, как и имена переменных.
Величина — переменная, с которой связывается определенное множество значений. Этой величине присваивается имя (в языках программирования его называют идентификатор).
Значение — то, чему равна переменная в конкретный момент. Значение переменной можно задать двумя способами: присваиванием и с помощью процедуры ввода.
Тип переменной определяет диапазон всех значений, которые может принимать данная переменная, и допустимые для нее операции. Существует несколько предопределенных типов переменных. К стандартным типам относятся числовые, литерные и логические типы.
Числовой тип предназначен для обработки числовых данных. Различают целый и вещественный числовые типы. Целый тип в учебном алгоритмическом языке обозначается служебным словом цел, к нему относятся целые числа некоторого определенного диапазона. Они не могут иметь дробной части, даже нулевой. Число 123,0 является не целым, а вещественным числом. Вещественные величины относятся к вещественному типу данных и обозначаются в учебном алгоритмическом языке служебным словом вещ. Такие величины могут отображаться двумя способами: в форме с фиксированной запятой (например, 0,0511 или –712,3456) и с плавающей запятой (те же примеры: 5,11*10-2 и –7,123456*102).
Над числовыми данными можно выполнять арифметические операции и операции сравнения.

Над целыми числами можно также выполнять две операции целочисленного деления div и mod. Операция div обозначает деление с точностью до целых чисел (остаток от деления игнорируется). Операция mod позволяет узнать остаток при делении с точностью до целых чисел. Например, результатом операции 100 div 9 будет число 11, а результатом 100 mod 9 — число 1.
Литерный тип представляет собой символы и строки, он дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов. Эти последовательности заключаются в двойные кавычки: «результат», «sum_price». В качестве символов могут быть использованы буквы, цифры, знаки препинания, пробел и некоторые другие специальные знаки (возможными символами могут быть символы таблицы ASCII). В учебном алгоритмическом языке литерные величины обозначаются лит.
Над литерными величинами возможны операции сравнения и слияния. Сравнение литерных величин производится в соответствии с их упорядочением: «a» < «b», «b» < «с» и т. д. Слияние (конкатенация) литерных величин приводит к образованию новой величины: «пол» + «е» образует «поле».
Логический тип определяет логические переменные, которые могут принимать только два значения — истина (True) или ложь (False). Над логическими величинами можно выполнять все стандартные логические операции.
Команды учебного алгоритмического языка
Учебный алгоритмический язык использует следующие команды для реализации алгоритма:

ОПЕРАЦИЯ ПРИСВАИВАНИЯ
Ко всем типам величин может быть применена операция присваивания, которая обозначается знаком «:=» и служит для вычисления выражения, стоящего справа, и присваивания его значения переменной, указанной слева. Например, если переменная H имела значение 12, а переменная М — значение 3, то после выполнения оператора присваивания H := М + 10 значение переменной H изменится и станет равным 13.
Вычисления в операторе присваивания выполняются справа налево: сначала необходимо вычислить значение выражения справа от знака присваивания. Поэтому допустимы конструкции вида H := Н + 10. В этом случае сначала будет вычислено выражение в правой части (12 + 10), а его результат будет присвоен в качестве нового значения переменной Н (значение 22).
Для оператора присваивания обязательно должны быть определены значения всех переменных в его правой части. Кроме того, типы данных в левой и правой части должны соответствовать друг другу.
ВВОД И ВЫВОД ДАННЫХ
В процессе работы алгоритма происходит обработка исходных данных для получения выходных (результирующих) данных. В процессе этого преобразования могут быть найдены некоторые промежуточные результаты. Входные данные должны быть переданы алгоритму («введены»), а по окончании работы алгоритм должен вывести результат.
При записи алгоритма с помощью блок–схемы ввод и вывод данных отображаются с помощью блоков ввода/вывода (параллелограммов). При этом только указывается перечень данных для ввода или вывода, а сам процесс не детализируется.
Описание алгоритма средствами псевдокода может вовсе не предусматривать команды ввода или вывода данных. В заголовке алгоритма указывается, какие данные являются аргументами, какие — результатами работы алгоритма. Считается, что аргументы будут предоставлены до выполнения алгоритма, результаты будут выведены после его выполнения, и описывается лишь процесс превращения аргументов в результаты.
В записи алгоритма с помощью учебного алгоритмического языка для операций ввода/вывода используются команды ввод и вывод. После этих служебных слов указывается список ввода или вывода. Элементы этих списков перечисляются через запятую.
Список ввода может содержать только имена переменных. После выполнения команды ввод алгоритм получит значения перечисленных в списке переменных.
