Какое свойство называется существенным

Объем и содержание понятий
Термин «понятие» применяется обычно для обозначения целого класса объектов произвольной природы, которые обладают определенным характеристическим (отличительным, существенным) свойством или целым набором таких свойств, т.е. свойств, присущих только элементам этого класса.
С точки зрения логики понятие является особой формой мышления, характерным для которой является следующее: 1) понятие – продукт высокоорганизованной материи; 2) понятие отражает материальный мир; 3) понятие предстает в сознании как средство обобщения; 4) понятие означает специфически человеческую деятельность; 5) формирование понятия в сознании человека неотделимо от его выражения посредством речи, записи или символа.
Как возникает в нашем сознании понятие о каком-либо объекте действительности?
Процесс формирования некоторого понятия – постепенный процесс, в котором можно усмотреть несколько последовательных стадий. Рассмотрим этот процесс на простейшем примере – формирование у детей понятия о числе 3.
1. На первой ступени познания дети знакомятся с различными конкретными множествами, при этом используются предметные картинки и демонстрируются различные множества из трех элементов (три яблока, три книги, три карандаша и т.п.). Дети не только видят каждое из этих множеств, но и могут осязать (потрогать) те предметы, из которых эти множества состоят. Этот процесс «видения» создает в сознании ребенка особую форму отражения реальной действительности, которая называется восприятием (ощущением).
2. Уберем объекты (предметы), составляющие каждое множество, и предложим детям определить, было ли нечто общее, характеризующее каждое множество. В сознании детей должно было запечатлеться число предметов в каждом множестве, то, что везде было по «три». Если это так, то в сознании детей создалась новая форма – представление о числе «три».
3. На следующей стадии, на основе мыслительного эксперимента дети должны усмотреть, что свойство, выраженное в слове «три», характеризует любое множество различных элементов вида {a; b; c}. Тем самым будет выделена существенная общая особенность таких множеств – «иметь три элемента». Теперь можно сказать, что в сознании детей сформировано понятие о числе 3.
Понятие – это особая форма мышления, в которой отражены существенные (отличительные) свойства предметов или объектов изучения.
Языковой формой понятия является слово или группа слов. Например, «треугольник», «число три», «точка», «прямая», «равнобедренный треугольник», «растение», «хвойное дерево», «река Енисей», «стол» и т. д.
Математические понятия обладают рядом особенностей. Главная заключается в том, что математические объекты, о которых необходимо составить понятие, в реальности не существуют. Математические объекты созданы умом человека. Это идеальные объекты, отражающие реальные предметы или явления. Например, в геометрии изучают форму и размеры предметов, не принимая во внимание другие их свойства: цвет, массу, твердость и т.д. От всего этого отвлекаются, абстрагируются. Поэтому в геометрии вместо слова «предмет» говорят «геометрическая фигура». Результатом абстрагирования являются и такие математические понятия, как «число» и «величина».
Основными характеристиками любого понятия являются следующие: 1) объем; 2) содержание; 3) отношения между понятиями.
Когда говорят о математическом понятии, то обычно имеют в виду всю совокупность (множество) объектов, обозначаемых одним термином (словом или группой слов). Так, говоря о квадрате, имеют в виду все геометрические фигуры, являющиеся квадратами. Считают, что множество всех квадратов составляет объем понятия «квадрат».
Объемом понятия называется множество объектов или предметов, к которым применимо данное понятие.
Например, 1) объемом понятия «параллелограмм» является множество таких четырехугольников, как собственно параллелограммы, ромбы, прямоугольники и квадраты; 2) объемом понятия «однозначное натуральное число» будет множество – {1, 2, 3, 4, 5, 6, 7, 8, 9}.
Любой математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла, равные диагонали, диагонали точкой пересечения делятся пополам. Можно указать и другие его свойства, но среди свойств объекта различают существенные (отличительные) и несущественные.
Свойство называется существенным (отличительным) для объекта, если оно присуще этому объекту и без него он не может существовать; свойство называется несущественным для объекта, если он может без него существовать.
Например, для квадрата существенными являются все свойства, перечисленные выше. Несущественным для квадрата АВСD будет свойство «сторона АD горизонтальна» (рис. 1). Если этот квадрат повернуть, то сторона АD окажется вертикальной.
В С А В
А D D С
Рис.1
Рассмотрим пример для дошкольников, используя наглядный материал (рис. 2):
Диалог:
– Опиши фигуру.
– Маленький черный треугольник. Рис. 2
– Большой белый треугольник.
– Чем фигуры похожи ?
– Формой.
– Чем фигуры отличаются ?
– Цветом, величиной.
– Что есть у треугольника ?
– 3 стороны, 3 угла.
Таким образом, дети выясняют существенные и несущественные свойства понятия «треугольник». Существенные свойства – «иметь три стороны и три угла», несущественные свойства – цвет и размеры.
Совокупность всех существенных (отличительных) свойств объекта или предмета, отраженных в данном понятии, называют содержанием понятия.
Например, для понятия «параллелограмм» содержанием является множество свойств: имеет четыре стороны, имеет четыре угла, противоположные стороны попарно параллельны, противоположные стороны равны, противоположные углы равны, диагонали в точки пересечения делятся пополам.
Между объемом понятия и его содержанием существует связь: если увеличивается объем понятия, то уменьшается его содержание, и наоборот. Так, например, объем понятия «равнобедренный треугольник» является частью объема понятия «треугольник», а в содержание понятия «равнобедренный треугольник» входит больше свойств, чем в содержание понятия «треугольник», т.к. равнобедренный треугольник обладает не только всеми свойствами треугольника, но и другими, присущими только равнобедренным треугольникам («две стороны равны», «два угла равны», «две медианы равны» и др.).
По объему понятия подразделяются на единичные, общие и категории.
Понятие, объем которого равен 1, называется единичным понятием.
Например, понятия: «река Енисей», «Республика Тува», «город Москва».
Понятия, объем которых больше 1, называются общими.
Например, понятия: «город», «река», «четырехугольник», «число», «многоугольник», «уравнение».
В процессе изучения основ какой-либо науки у детей формируются, в основном, общие понятия. Например, в начальных классах учащиеся знакомятся с такими понятиями, как «цифра», «число», «однозначные числа», «двузначные числа», «многозначные числа», «дробь», «доля», «сложение», «слагаемое», «сумма», «вычитание», «вычитаемое», «уменьшаемое», «разность», «умножение», «множитель», «произведение», «деление», «делимое», «делитель», «частное», «шар», «цилиндр», «конус», «куб», «параллелепипед», «пирамида», «угол», «треугольник», «четырехугольник», «квадрат», «прямоугольник», «многоугольник», «круг», «окружность», «кривая», «ломаная», «отрезок», «длина отрезка», «луч», «прямая», «точка», «длина», «ширина», «высота», «периметр», «площадь фигуры», «объём», «время», «скорость», «масса», «цена», «стоимость» и многими другими. Все эти понятия являются общими понятиями.
К категориям относятся понятия широкой степени общности («материя», «движение», «причина», «следствие» и т.д.).
Источник
Существенные и несущественные свойства
математических объектов раскрываются в процессе
определения понятий математики. Множество
существенных свойств составляют содержание
понятия.
Под существенными свойствами будем понимать
те, без которых понятие не существует, и при
помощи которых выделяются объекты интересующего
нас множества. Существенные свойства – это
всегда общие свойства, но обратное неверно –
общие свойства могут быть несущественными. Так, в
школьных учебниках в уравнениях преобладает
обозначение переменной – “х”. Это свойство
общее, но не существенное.
Кроме того, понятия “существенное” и
“несущественное” свойство относительны, в
разных ситуациях одно и то же свойство
математического объекта может быть как
существенным, так и несущественным. Например, при
выделении линейных функций среди других знак
коэффициента при х – несущественное
свойство, но оно же становится существенным при
выделении среди линейных функций возрастающих.
Существенные свойства понятия в определении
могут быть связаны между собой конъюнктивно,
дизъюнктивно и в сочетании конъюнкции и
дизъюнкции. Большинство школьных определений –
конъюнктивны. Если
– существенные свойства какого-либо
математического понятия Р, то:
• если математический объект не обладает хотя
бы одним из свойств , то этот объект не принадлежит понятию Р;
• если математический объект обладает всеми
существенными свойствами , то он обязательно принадлежит
понятию Р.
Понять эту непростую закономерность ребятам
помогает такое объяснение материала, при котором
после введения определения ученикам
предъявляются математические объекты со
свойствами ; . Учащиеся
должны мотивированно ответить на вопрос, почему
эти объекты не принадлежат понятию Р. Такая
работа позволяет за один урок сформировать в
сознании ребят математическое понятие.
Процесс выделения свойств математических
объектов, отделения существенных от
несущественных очень сложен. Чтобы помочь в этом,
можно применять на уроках задания следующих
четырех типов.
Первый из них – учащимся известно определение
математического понятия и они с помощью учителя
или самостоятельно формулируют основные
существенные свойства этого понятия, заем
проверяют, обладают ли предложенные им
математические объекты этими свойствами.
Примером могут служить следующие задания:
• Сформулируйте определение линейной функции.
Укажите, какая из следующих функций является
линейной, а какая – нет. Поясните, почему?
; ; ; ; ; ; ; ; ; .
• Сформулируйте известные вам свойства
понятия функции. Укажите, какая из ломаных,
изображенных на рисунке, является графиком
функции:
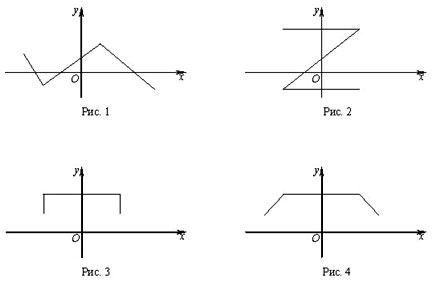
Поясните свой ответ.
Задания второго типа состоят в том, что
учащиеся должны назвать математический объект
по перечисленным его свойствам.
1. Функция … принимает наибольшее значение при .
2. Функция … возрастает на интервале и убывает на
интервале .
3. График функции … симметричен относительно
прямой .
4. График функции … расположен в III и IV
координатных четвертях.
5. График функции … проходит через точку .
6. Точка пересечения графика функции … с осью ОУ
– .
Какая квадратичная функция обладает этими
свойствами? Задайте ее аналитической формулой и
постройте график этой функции.
Задания третьего типа – это задания, в которых
нужно выделить существенные свойства
математических объектов и привести
самостоятельно примеры объектов, обладающих
такими же свойствами или отбросить лишние
объекты:
• Какое из числовых выражений вы назвали бы
лишним в этой таблице?
Поясните свой ответ.
• Запишите еще несколько членов числовой
последовательности, задайте ее общий член
формулой:
.
В заданиях четвертого типа от учащихся
требуется добавить свойство или свойства, чтобы
от одного математического объекта перейти к
другому. На уроках геометрии предлагается
задание:
• Укажите то условие, которое нужно добавить,
чтобы от одного четырехугольника перейти к
другому. Назовите все известные вам свойства
перечисленных геометрических фигур.
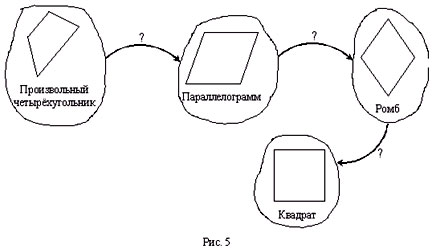
• Укажите условия, необходимые для того, чтобы
перейти от одной функции к другой. Назовите все
известные вам свойства указанных функций.
Прием расчленяющей абстракции (Е.Н.
Кобанова-Меллер) при изучении понятий выражается
в таких действиях:
а) выделяются существенные свойства
математических объектов, они остаются
инвариантными в процессе формирования понятия;
б) выделяются несущественные свойства тех же
объектов и принцип их вариаций, в процессе
формирования понятия используются вариации
несущественных свойств.
После знакомства с графиками функций,
содержащих модули, можно предложить учащимся
графически решить уравнение, содержащее модуль и
параметр.
• Найти все значения а, при которых
уравнение имеет
ровно два корня.
Данное уравнение имеет вид , где ; .
Раскрывая знаки модулей в , рассмотрим три случая:
1) : .
2) : .
3) : .
Запишем в
виде:
Решим данное уравнение графически, построив в
системе координат ОХУ графики функций и . Заметим, что задает множество прямых,
параллельных оси ОХ.
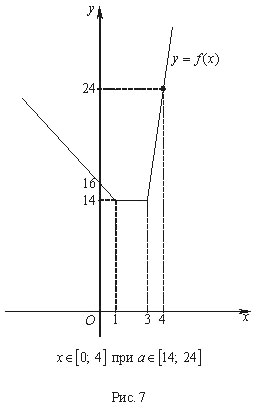
Решением задачи будет промежуток .
Учитель может варьировать задания:
• Найти все а, при которых уравнение
1) имеет ровно два корня;
2) имеет ровно три корня;
3) имеет бесконечно много корней;
4) не имеет корней;
5) имеет хотя бы одни корень;
6) имеет хотя бы один корень, причем все его
корни принадлежат отрезку .
Другое направление варьирования исходного
задания – изменять :
• Найти все а, при которых уравнение:
1)
2)
3)
имеет два корня.
Наконец, варьированию поддаются функции,
входящие в левую часть исходного уравнения:
• Найти все а, при которых уравнение:
1)
2)
3)
имеет ровно два корня.
Из получившихся заданий учитель может выбрать
материал для “Урока одной задачи”, учитывая
особенности своего класса.
Источник
Беседа 5. Математические понятия и их определения
Всякий математический объект обладает какими-то свойствами. Так, например, треугольник обладает такими свойствами: имеет три стороны; 2) три внутренних угла; 3) шесть попарно равных внешних углов и т. д. Подобные утверждения о наличии или отсутствии у данного объекта какого-либо свойства называются суждениями. Вот еще примеры суждений: 1) четырехугольник имеет две диагонали; 2) за каждым натуральным числом непосредственно следует в натуральном ряду другое натуральное число; 3) четное число делится на два и т. д.
Суждениями являются также предложения, указывающие на отношения или связи объектов, например: “5 больше 3”, “АВ является стороной треугольника ABC“, “Угол А не является смежным с углом В” и т. д. А вот вопросы или требования не являются суждениями.?
Среди свойств какого-либо объекта имеются существенные и несущественные для его определения. Свойство является существенным, если оно присуще этому объекту и без него оно не может существовать. Несущественные свойства – это обычно случайные, их отсутствие, как правило, не влияет на существование объекта. Заметим, что при решении конкретных задач несущественные вообще свойства объектов могут иметь и существенное значение для решения данной задачи.

Рис. 3
Рассмотрим, например, равнобедренный треугольник, изображенный на рис. 3. Его свойства: 1) стороны треугольника АВ и ВС равны; 2) медиана BD перпендикулярна основанию АС и делит угол В пополам – это существенные свойства этого треугольника. А вот свойства: 3) основание АС равнобедренного треугольника ABC горизонтально или 4) вершина равнобедренного треугольника обозначена буквой В – являются несущественными. Если мы как-то повернем этот треугольник и его основание при этом окажется расположено не горизонтально или обозначим вершину какой-то другой буквой, то ведь треугольник не перестанет быть равнобедренным.
Поэтому, чтобы понимать, что это за объект, достаточно знать его существенные свойства. В этом случае говорят, что имеется понятие об этом объекте. Следовательно, понятие – это целостная совокупность суждений о существенных свойствах соответствующего объекта. Эта совокупность взаимосвязанных свойств объекта (поэтому она называется целостной) называется содержанием понятия об этом объекте.
Заметим, что когда говорят о математическом объекте, то обычно имеют в виду все множество объектов, обозначаемых одним термином (названием). Так, когда говорят о математическом объекте – треугольнике, то имеют в виду все геометрические фигуры, являющиеся треугольниками. Множество всех треугольников составляет объем понятия о треугольнике. Точно так же множество всех натуральных чисел составляет объем понятий о натуральном числе. Следовательно, объем понятия – это множество всех объектов, обозначаемых одним и тем же термином.
Итак, всякое понятие имеет определенный объем и содержание. Они взаимосвязаны: чем больше объем понятия, тем меньше его содержание, и наоборот: чем меньше объем, тем больше содержание понятия. Так, например, объем понятия “равнобедренный треугольник” меньше объема понятия “треугольник”, ибо в объем первого понятия входят не все треугольники, а лишь равнобедренные. А вот содержание первого понятия, очевидно, больше содержания второго, ибо равнобедренный треугольник обладает не только всеми свойствами треугольника, но и особыми свойствами, присущими только равнобедренным треугольникам.
В содержание понятия о каком-либо математическом объекте входят много различных существенных свойств этого объекта. Однако, для того чтобы распознать объект, установить, принадлежит ли он к данному понятию или нет, достаточно проверить наличие у него лишь некоторых существенных свойств. Указание этих существенных свойств объекта понятия, которые достаточны для распознавания этого объекта, называется определением понятия.
Всякое определение математического понятия строится обычно так: сначала указывается название объекта этого понятия, затем перечисляются такие его существенные свойства, которые позволяют установить, является ли тот или иной предмет объектом данного понятия или нет.
Например, определение параллелограмма: “Параллелограммом называется четырехугольник, противоположные стороны которого параллельны”. Как видим, это определение построено так: сначала указано название объекта определяемого понятия – параллелограмм, затем указаны такие его свойства: 1) параллелограмм – это четырехугольник; 2) противоположные его стороны параллельны. Первое свойство – это указание того более общего понятия, к которому принадлежит определяемое понятие. Это более общее понятие называется родовым по отношению к определяемому понятию. В данном случае родовым понятием для параллелограмма является четырехугольник. Второе свойство – это указание видового свойства, которое отличает параллелограмм от других видов четырехугольника. Вот еще пример определения: “Четными числами называются такие натуральные числа, которые кратны числу 2”. Это определение, так же как и предыдущее, построено по такой схеме:

В данном случае мы имеем: название определяемого понятия – четные числа, родовое понятие – натуральные числа, видовые отличия – кратны числу 2.
Определение понятий по этой схеме называется определением через род и видовые отличия.
Иногда в математике встречаются и другие способы определения понятий. Рассмотрим, например, определение треугольника: “Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков”. В этом определении указано родовое понятие для треугольника – фигура, а в качестве видового отличия указан способ построения такой фигуры, которая является треугольником: нужно взять три точки, не лежащие на одной прямой, и соединить каждую их пару отрезком. Такое определение называется генетическим (от слова генезис – происхождение). Вот еще пример генетического определения: “Симметрией относительно точки называется такое преобразование фигуры F в фигуру F’ при котором каждая точка X фигуры F переходит в точку X’ фигуры F’, построенной следующим образом: на продолжении отрезка ОХ за точку О откладывается отрезок ОХ’, равный ОХ“. Здесь в качестве видовых отличий преобразования симметрии относительно точки от других видов преобразований указан способ построения точек фигуры F’, симметричной фигуре F относительно точки О.
Встречаются в математике и такие определения, в которых указывается, как можно получить объекты определяемого понятия один за другим по порядку. Например, определение арифметической прогрессии дается таким образом: “Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией”. Здесь определяемое понятие – арифметическая прогрессия, родовое понятие – числовая последовательность, в качестве видового отличия указан способ получения всех членов прогрессии, начиная со второго, состоящий в том, что для получения какого-либо члена надо к предшествующему члену прибавить одно и то же число. Это определение можно записать в виде следующей формулы:
Такое определение называется индуктивным (от слова индукция – наведение на умозаключение от частного к общему) или рекуррентным (от слова рекурсия – возвращение).
Однако не все математические понятия могут быть логически определены указанными выше способами. Действительно, каждое определение математического понятия сводит определяемое понятие к более широкому (более общему, т. е. имеющему больший объем) родовому понятию, определение родового понятия сводит его к еще более широкому понятию и т. д. Очевидно, что этот процесс сведения одних понятий к более широким, более общим понятиям должен иметь конец, он не может быть бесконечным. Иными словами, в конечном итоге определения понятий мы должны прийти к таким понятиям, которые уже не сводимы к другим, т. е. они логически не определяемы. Такие понятия в математике называются первичными или основными.
Например, определяя параллелограмм, мы сводим его к понятию четырехугольника, определяя четырехугольник, мы сводим его к понятию многоугольника, затем к понятию геометрической фигуры, которая сводится при определении к понятию точки. Понятие точки уже является не определяемым, т. е. первичным. Первичными понятиями в математике, кроме точки, являются понятия прямой, плоскости, принадлежать, числа, множества (совокупность) и некоторые другие.
Итак, второе, чему нужно научиться в математике, – это умению строить определения математических понятий каким-либо способом. Это умение довольно сложное, и мы о нем поговорим еще в следующей беседе. А пока выполните следующее задание, чтобы закрепить те сведения, которые вы получили в данной беседе.
Задание 3
3.1. Какие из приведенных ниже свойств трапеции являются существенными, а какие несущественными:
а) Две стороны трапеции параллельны.
б) Оба угла при большем основании острые.
в) Сумма углов трапеции, принадлежащих к одной боковой стороне, равна 180°.
г) Основания трапеции горизонтальны.
д) Оба угла при меньшем основании трапеции тупые.
3.2. Как связаны между собой математические объекты и математические понятия?
3.3.Укажите, какие из приведенных ниже предложений являются суждениями, а какие ими не являются:
а) В треугольнике проведены три медианы.
б) Медианы треугольника пересекаются в одной точке.
в) Чему равно произведение степеней с одинаковыми основаниями?
г) Логарифм произведения положительных чисел равен сумме логарифмов множителей.
3.4. В приведенных ниже определениях выделите название объектов определяемых понятий, родовое понятие и видовые отличия:
а) Числа, которые можно записать в виде обыкновенных дробей, называются рациональными.
б) Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
в) Две прямые на плоскости называются параллельными, если они не пересекаются.
г) Если точка О является серединой отрезка АВ, то точки A и В называются симметричными точками относительно точки О.
3.5. Сформулируйте генетическое определение окружности, зная, что она образуется в результате вращения отрезка на плоскости вокруг одного из его концов, второй конец этого отрезка в этом случае описывает окружность.
3.6. Члены последовательности Фибоначчи (ок. 1170-1250) задаются с помощью следующей формулы: аn+2=аn+1+an. Сформулируйте определение этой последовательности. Какое это определение?
3.7. Приводим следующее описание построения перпендикулярных прямых: “Пусть а и b – две пересекающиеся прямые. При их пересечении образуются четыре угла. Пусть α – один из этих углов. Тогда любой из остальных трех углов будет либо смежным с углом α, либо вертикальным с углом α. Отсюда следует, что если один из углов прямой, то остальные углы тоже прямые. В этом случае мы говорим, что прямые пересекаются под прямым углом, и называем их перпендикулярными“.
На основе этого описания сформулируйте определение перпендикулярных прямых.
3.8. Модуль числа определяется следующей формулой:
Сформулируйте словесное определение модуля числа.
3.9. Последовательность называется возрастающей, если каждый ее член больше предыдущего члена. Запишите это определение с помощью формулы.
3.10.Как вы знаете, равнобедренный треугольник – это такой треугольник, у которого две стороны равны, а правильный треугольник – это такой, у которого все стороны равны. Является ли правильный треугольник равнобедренным?
3.11. Укажите ближайшие родовые понятия для следующих понятий: а) квадрат; б) степень с натуральным показателем; в) вертикальные углы; г) простое число; д)хорда.
3.12. Укажите несколько родовых понятий для понятия ромб.
3.13. Нужно ли (и можно ли) доказывать определения?
Источник
