Какое свойство магнитной цепи является главным
Работа всех электромагнитных устройств (трансформаторов, электрических машин, измерительных приборов, реле, контакторов, выключателей и т.д.) основана на использовании магнитного поля. Магнитное поле возникает в пространстве, окружающем движущиеся электрические заряды и постоянные магниты.
Виды воздействия магнитного поля на тела, помещенные в него:
1. Индукционное, т.е. при перемещении проводника в постоянном магнитном поле или если магнитное поле пересекает проводник (при изменении магнитного поля вокруг проводника), в нем наводится ЭДС . Направление ЭДС определяется по «правилу правой руки» (рис. 2.1) Если поставить правую руку так, чтобы магнитные линии входили в ладонь, а отогнутый большой палец указывал направление движения проводника, то вытянутые четыре пальца укажут направление индуцируемой ЭДС Индукционное воздействие магнитного поля используется в работе трансформаторов, электрических генераторов, электроизмерительных приборов;
2. Электромеханическое (силовое), т.е. проводник с током или ферромагнитное тело, помещенное в магнитное поле, испытывают действие силы F со стороны этого поля. Силовое воздействие магнитного поля используется в работе двигателей, электроизмерительных приборов, реле, выключателей, контакторов и т.д.
Величины, характеризующие магнитное поле:
2) Магнитная индукция В – векторная величина, характеризующая интенсивность магнитного поля и определяющая силу, действующую на движущую заряженную частицу.
Вектор магнитной индукции направлен по касательной к магнитным силовым линиям. Единица измерения – тесла (Тл). Направление электромагнитной силы F, действующей на проводник с током, определяется «правилом левой руки» (рис. 2.2): если расположить левую руку так, чтобы магнитные линии пронизывали ладонь, а вытянутые четыре пальца указывали направление тока в проводнике, то отогнутый большой палец укажет направление действия электромагнитной силы;
2. Магнитный потокФ – поток вектора магнитной индукции В через площадь S: . Единица измерения – вебер (Вб);
3. НамагниченностьМ – магнитный момент единицы объема вещества;
4. Напряженность магнитного поляН – векторная величина, характеризующая способность тока возбуждать магнитное поле, приходящаяся на единицу длины магнитной силовой линии: .
Единица измерения А/м.
Связь между вышеперечисленными величинами:
или ,
где Гн/м – магнитная постоянная,
–магнитная проницаемость среды (материала), которая показывает качество ферромагнитного материала, т.е. его способность «проводить» магнитный поток.
В воздухе , в ферромагнитном материале поскольку нелинейно зависит от напряженности магнитного поля .
Следовательно: ферромагнитные материалы обладают свойством усиливать магнитное поле.
Для увеличения эффективности работы электротехнических устройств магнитное поле в них сосредотачивают и усиливают, применяя магнитопроводы из ферромагнитных материалов, по которым замыкается магнитный поток.
В каждом электромагнитном устройстве можно выделить магнитную цепь.
Магнитная цепь – это совокупность элементов, возбуждающих магнитное поле (катушка с током, постоянный магнит), магнитопроводов и воздушных зазоров, которые предназначены для создания магнитного поля требуемой интенсивности, конфигурации и направления в электротехническом устройстве.
В однородной магнитной цепи Ф, В, Н, S=const. В основном магнитные цепи электротехнических устройств являются неоднородными. В неразветвленной магнитной цепи с зазором Ф, В, S=const, однако напряженность магнитного поля в магнитопроводе и в воздушном зазоре разная . В разветвленной магнитной цепи по ее участкам замыкаются разные магнитные потоки.
В электротехнических устройствах применяют ферромагнитные материалы двух видов: магнитомягкие и магнитотвердые.
Магнитомягкие материалы с узкой петлей гистерезиса (рис. 2.3) обладают свойством легко перемагничиваться и используются для изготовления магнитопроводов магнитных систем электротехнических устройств.
Магнитотвердые материалы с широкой петлей гистерезиса (рис. 2.3) обладают свойством задерживать остаточную намагниченность и используются при изготовлении постоянных магнитов.
Рис. 2.3
Магнитомягкие материалы:
– технически чистое железо (низкоуглеродистая электротехническая сталь, обладающая низким удельным электрическим сопротивлением) используется в устройствах, работающих на постоянном токе и низкой частоте;
– листовая электротехническая сталь (железокремнистая сталь, обладающая высоким удельным электрическим сопротивлением за счет присадок кремния) используется в устройствах, работающих на переменном токе;
– пермаллои (железоникелевые сплавы, относительная магнитная проницаемость которых в сотни и тысячи раз выше, магнитная индукция насыщения в 1,5 – 2 раза меньше, коэрцитивная сила в 10-50 раз меньше, чем у электротехнических сталей) используются в малогабаритных устройствах;
– магнитомягкие ферриты и пермендюры.
Магнитотвердые материалы:
– магнитотвердые сплавы, получаемые на основе сплавов железа, никеля, алюминия, кобальта используются в роторах тахогенераторов, магнитных муфтах, измерительных приборах, реле, в радиоэлектронной аппаратуре;
– магнитотвердые ферриты используют при изготовлении магнитов, используемых в электронных приборах, микрогенераторах и д.р.
Рекомендуемые страницы:
Читайте также:
Источник
Магнитной цепью называется устройство, отдельные участки которого выполнены из ферромагнитных материалов, по которым замыкается магнитный поток. Примерами простейших цепей могут служить магнитопроводы кольцевой катушки и электромагнита, изображенного на рис. 6.11, а. Электрические машины и трансформаторы, электромагнитные аппараты и приборы имеют обычно магнитные цепи более сложной формы.
Рис. 6.11 Магнитные цепи (а — неразветвленная, б — разветвленная)
Если магнитная цепь выполнена из одного и того же материала и имеет по всей длине одинаковое сечение, то цепь называется однородной.
Если же отдельные участки цепи изготовлены из различных ферромагнитных материалов и имеют различные длины и сечения, то цепь — неоднородная.
Магнитные цепи, так же как и электрические, бывают разветвленные (рис. 6.11,6) и неразветвленные (рис. 6.11,а).
В неразветвленных цепях магнитный поток Ф во всех сечениях имеет одно и то же значение.
Разветвленные цепи могут быть симметричными и несимметричными. Цепь, представленная на рис. 6.11,6, считается симметричной, если правая и левая части ее имеют одинаковые размеры, выполнены из одного и того же материала и если МДС I1W1 и I2W2 одинаковы. При невыполнении хотя бы одного из указанных условий цепь будет несимметричной.
Разобьем неразветвленную магнитную цепь, например, на рис 6.11, а на ряд однородных участков, каждый из которых выполнен из определенного материала и имеет одинаковое поперечное сечение S вдоль всей своей длины. Длину каждого участка L будем считать равной длине средней магнитной линии в пределах этого участка. Из сказанного выше следует, что магнитные потоки всех участков неразветвленной цепи равны, т. е.
Ф1=Ф2=Ф3=…=Фn,
и поле на каждом участке можно считать однородным, т. е. Ф= BS; поэтому
B1S1=B2S2=B3S3=…=BnSn
Где n — число участков цепи. Магнитное напряжение на любом из участков магнитной цепи
Где H — Напряженность, (измеряется в ампер на метр А/М).
B — Магнитная индукция (измеряется в теслах Тл).
L — Длинна средне силовой линии проходящей через центр поперечного сечения магнитопровода.
S — площадь поперечного сечения магнитопровода.
— Магнитная постоянная.
μr — Магнитная проницаемость ферромагнетиков.
При заданном направлении тока в обмотке направление потока и МДС IW определяется по правилу буравчика.
Магнитное сопротивление и закон Ома для магнитной цепи.
По аналогии с электрической цепью величину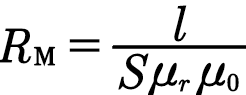
называют магнитным сопротивлением участка магнитной цепи (измеряется в 1/Гн).
Таким образом, магнитное напряжение
Выражение (3) по аналогии с электрической цепью часто называют законом Ома для магнитной цепи Однако вследствие нелинейности цепи, вызванной непостоянством магнитной проницаемости μr ферромагнетиков, оно практически не применяется для расчета магнитных цепей.
Законы Кирхгофа для магнитной цепи
При расчетах разветвленных магнитных цепей пользуются двумя законами Кирхгофа, аналогичными законам Кирхгофа для электрической цепи.
Первый закон Кирхгофа непосредственно вытекает из непрерывности магнитных линий, т.е. и магнитного потока; алгебраическая сумма магнитных потоков в точке разветвления равна нулю:
Например, для узла а на рис. 6.11,б
— Ф1 — Ф2 + Ф3 = 0
Второй закон Кирхгофа для магнитной цепи основывается на законе полного тока: алгебраическая сумма магнитных напряжений на отдельных участках цепи равна алгебраической сумме МДС:
Например, для левого контура и а рис. 6.11, б
Как следует из закона Ома, для получения наибольшего магнитного потока при наименьшей МДС у магнитной цепи должно быть возможно меньшее магнитное сопротивление. Большая магнитная проницаемость ферромагнитных материалов обеспечивает получение малых магнитных сопротивлений магнитопроводов из этих материалов. Поэтому магнитные цепи электрических машин выполняют преимущественно из ферромагнетиков, а участки цепей из неферромагнитных материалов, то есть неизбежные или необходимые воздушные зазоры, делают, как правило, возможно малыми.
Схема устройства магнитной цепи двухполюсной машины с явно выраженными полюсами показана на рис. 6.12.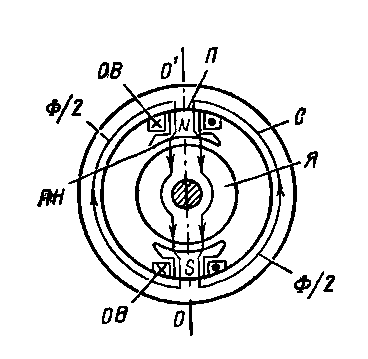
Рис. 6.12 Магнитная цепь электрической машины с явно выраженными полюсами
Плоскость 00′, проведенная через середины полюсов N и S и ось машины, делит магнитную цепь на две симметричные части. В каждой из них магнитный поток Ф/2 замыкается через полюсы П, полюсные наконечники ПН, воздушные зазоры, якорь Я и станину машины С. Магнитодвижущая сила создается током в обмотке возбуждения ОВ, расположенной на полюсах N и S. Из северного полюса N магнитные линии выходят и в южный полюс S входят.
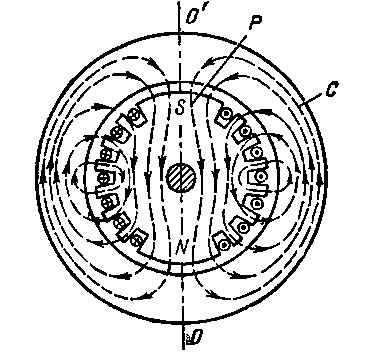
Рис, 6.13. Магнитная цепь электрической машины с неявно выраженными полюсами
Схема устройства магнитной цепи двухполюсной машины с неявно выраженными полюсами показана на рис. 6.13. Здесь обмотка возбуждения заложена в пазы ротора Р — вращающейся части машины, укрепленной на валу. Как и в предыдущем случае, плоскость 00′, проведенная через середины полюсов N и S, делит магнитную цепь машины на две симметричные части, в каждой из которых магнитный поток Ф/2. Магнитный поток замыкается через ротор машины, воздушные зазоры и станину машины С, представляющую собой неподвижный наружный стальной цилиндр — статор машины.
Источник
Основные понятия и законы магнитных цепей
Основы > Теоретические основы электротехники
Основные понятия и законы магнитных цепей
Совокупность устройств, содержащих ферромагнитные тела и образующих замкнутую систему, в которой существует магнитный поток и вдоль которой замыкаются линии магнитной индукции, называется магнитной цепью.
Магнитное поле в вещественных средах описывается тремя векторами:
1) вектором магнитной индукции В, характеризующим силовое действие магнитного поля на ток по закону Ампера, а при изменении магнитного поля – возбуждение электрического поля по закону электромагнитной индукции (Фарадея);
2) вектором намагниченности материала М, выражающим магнитный момент единицы объема намагниченного вещества или сумму магнитных моментов элементарных магнитных диполей в единице его объема;
3) вектором напряженности магнитного поля Н, который выражается через первые два вектора как разность этих векторов, взятых с соответствующими коэффициентами, зависящими от выбранной системы единиц измерения. В системе СИ
где
Гн/м – магнитная постоянная.
При расчете магнитных цепей основными скалярными величинами, характеризующими магнитную цепь, являются:
1) магнитный поток Ф, который определяется как поток вектора магнитной индукции через поверхность поперечного сечения магнитопровода:
2) магнитодвижущая сила (МДС) F, которая выражается через электрический ток i в проводах, обмотках и т. д., создающий магнитное поле:
где w – число витков катушки.
В качестве положительного направления магнитного потока через элемент поверхности выбирается направление вектора dS, а в качестве положительного направления МДС – направление вектора поверхности S, ограниченной контуром тока i, при правовинтовой системе координат или по правилу правого винта. Направление магнитного потока относительно тока определяется тем же правилом. В основе расчета магнитной цепи лежат два закона:
1) закон непрерывности линий магнитной индукции
или при охвате поверхностью S нескольких сечений магнитопровода
Этот закон аналогичен первому закону Кирхгофа для электрической цепи;
2) закон полного тока
Этот закон аналогичен второму закону Кирхгофа, так как интеграл по контуру
l можно представить в виде суммы криволинейных интегралов на участках цепи, например от точки а к точке b, каждый из которых можно по аналогии с электрической цепью назвать магнитным напряжением
В результате уравнение (24.6) может быть записано аналогично уравнению второго закона Кирхгофа для нелинейной электрической цепи
Единицы магнитных величин в системе СИ: магнитный поток – вебер (
), магнитная индукция – тесла (
), намагниченность и напряженность магнитного поля – ампер на метр (1 А/м), магнитное напряжение – ампер (1 А).
Роль вольт-амперных характеристик элементов нелинейных электрических цепей в магнитных цепях играют ампер-веберные характеристики 
, которые чаще принято выражать в виде вебер-амперных характеристик .
При построении этих характеристик для каждого из участков магнитной цепи необходимо знать свойства материала, выражаемые зависимостью В (Н). Для немагнитного участка магнитной цепи (воздух, диэлектрик, немагнитные проводящие материалы) намагниченность 
и 
. Для ферромагнетиков эта зависимость значительно сложнее и задается экспериментально полученными характеристиками магнитных материалов.
Источник
Ïîä òåðìèíîì “ìàãíèòíîå ïîëå” ïðèíÿòî ïîäðàçóìåâàòü îïðåäåëåííîå ýíåðãåòè÷åñêîå ïðîñòðàíñòâî, â êîòîðîì ïðîÿâëÿþòñÿ ñèëû ìàãíèòíîãî âçàèìîäåéñòâèÿ. Îíè âëèÿþò íà:
îòäåëüíûå âåùåñòâà: ôåððèìàãíåòèêè (ìåòàëëû ïðåèìóùåñòâåííî ÷óãóíû, æåëåçî è ñïëàâû èç íèõ) è èõ êëàññ ôåððèòîâ âíå çàâèñèìîñòè îò ñîñòîÿíèÿ;
äâèæóùèåñÿ çàðÿäû ýëåêòðè÷åñòâà.
Ôèçè÷åñêèå òåëà, îáëàäàþùèå ñóììàðíûì ìàãíèòíûì ìîìåíòîì ýëåêòðîíîâ èëè äðóãèõ ÷àñòèö, íàçûâàþò ïîñòîÿííûìè ìàãíèòàìè. Èõ âçàèìîäåéñòâèå ïðåäñòàâëåíî íà êàðòèíêå ñèëîâûìè ìàãíèòíûìè ëèíèÿìè.
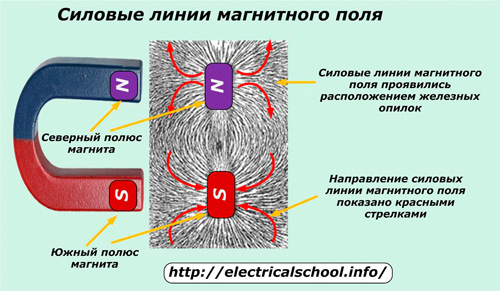
Îíè îáðàçîâàëèñü ïîñëå ïîäíåñåíèÿ ïîñòîÿííîãî ìàãíèòà ê îáðàòíîé ñòîðîíå êàðòîííîãî ëèñòà ñ ðîâíûì ñëîåì æåëåçíûõ îïèëîê. Êàðòèíêà äåìîíñòðèðóåò ÷åòêóþ ìàðêèðîâêó ñåâåðíîãî (N) è þæíîãî (S) ïîëþñîâ ñ íàïðàâëåíèåì ñèëîâûõ ëèíèé îòíîñèòåëüíî èõ îðèåíòàöèè: âûõîä èç ñåâåðíîãî ïîëþñà è âõîä â þæíûé.
Êàê ñîçäàåòñÿ ìàãíèòíîå ïîëå
Èñòî÷íèêàìè ìàãíèòíîãî ïîëÿ ÿâëÿþòñÿ:
ïîñòîÿííûå ìàãíèòû;
ïîäâèæíûå çàðÿäû;
èçìåíÿþùååñÿ âî âðåìåíè ýëåêòðè÷åñêîå ïîëå.
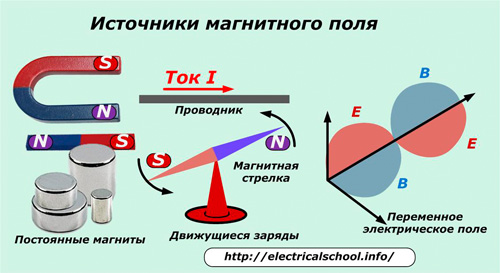
Ñ äåéñòâèåì ïîñòîÿííûõ ìàãíèòîâ çíàêîì êàæäûé ðåáåíîê äåòñàäîâñêîãî âîçðàñòà. Âåäü åìó óæå ïðèõîäèëîñü ëåïèòü íà õîëîäèëüíèê êàðòèíêè-ìàãíèòèêè, èçâëåêàåìûå èç óïàêîâîê ñ âñÿêèìè ëàêîìñòâàìè.
Íàõîäÿùèåñÿ â äâèæåíèè ýëåêòðè÷åñêèå çàðÿäû îáû÷íî îáëàäàþò çíà÷èòåëüíî áîëüøåé ýíåðãèåé ìàãíèòíîãî ïîëÿ, ÷åì ïîñòîÿííûå ìàãíèòû. Åãî òîæå îáîçíà÷àþò ñèëîâûìè ëèíèÿìè. Ðàçáåðåì ïðàâèëà èõ íà÷åðòàíèÿ äëÿ ïðÿìîëèíåéíîãî ïðîâîäíèêà ñ òîêîì I.
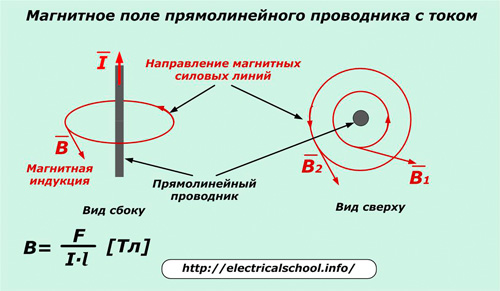
Ìàãíèòíàÿ ñèëîâàÿ ëèíèÿ ïðîâîäèòñÿ â ïëîñêîñòè, ïåðïåíäèêóëÿðíîé äâèæåíèþ òîêà òàê, ÷òîáû â êàæäîé åå òî÷êå ñèëà, äåéñòâóþùàÿ íà ñåâåðíûé ïîëþñ ìàãíèòíîé ñòðåëêè, íàïðàâëÿëàñü ïî êàñàòåëüíîé ê ýòîé ëèíèè. Òàêèì îáðàçîì ñîçäàþòñÿ êîíöåíòðè÷åñêèå îêðóæíîñòè âîêðóã äâèæóùåãîñÿ çàðÿäà.
Íàïðàâëåíèå ýòèõ ñèë îïðåäåëÿåòñÿ èçâåñòíûì ïðàâèëîì âèíòà èëè áóðàâ÷èêà ñ ïðàâîñòîðîííåé íàâèâêîé ðåçüáû.
Ïðàâèëî áóðàâ÷èêà
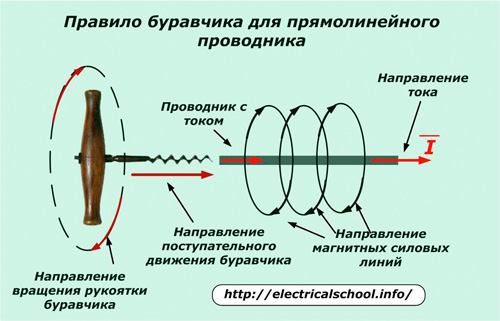
Íåîáõîäèìî ðàñïîëîæèòü áóðàâ÷èê ñîîñíî ñ âåêòîðîì òîêà è âðàùàòü ðóêîÿòêó òàê, ÷òîáû ïîñòóïàòåëüíîå äâèæåíèå áóðàâ÷èêà ñîâïàäàëî ñ åãî íàïðàâëåíèåì. Òîãäà îðèåíòàöèÿ ñèëîâûõ ìàãíèòíûõ ëèíèé áóäåò ïîêàçàíà âðàùåíèåì ðóêîÿòêè.
 êîëüöåâîì ïðîâîäíèêå âðàùàòåëüíîå äâèæåíèå ðóêîÿòêè ñîâïàäàåò ñ íàïðàâëåíèåì òîêà, à ïîñòóïàòåëüíîå óêàçûâàåò íà îðèåíòàöèþ èíäóêöèè.
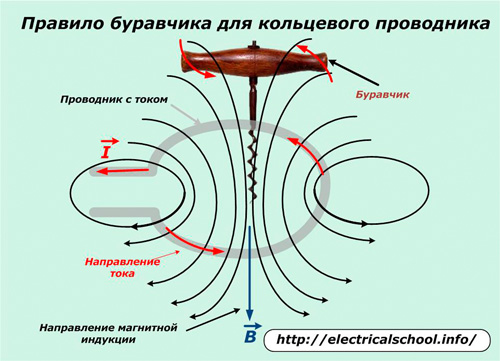
Ìàãíèòíûå ñèëîâûå ëèíèè âñåãäà âûõîäÿò èç ñåâåðíîãî ïîëþñà è âõîäÿò â þæíûé. Îíè ïðîäîëæàþòñÿ âíóòðè ìàãíèòà è íèêîãäà íå áûâàþò ðàçîìêíóòûìè.
Ïîäðîáíåå ñìîòðèòå çäåñü: Êàê ðàáîòàåò ïðàâèëî áóðàâ÷èêà â ýëåêòðîòåõíèêå
Ïðàâèëà âçàèìîäåéñòâèÿ ìàãíèòíûõ ïîëåé
Ìàãíèòíûå ïîëÿ îò ðàçíûõ èñòî÷íèêîâ ñêëàäûâàþòñÿ äðóã ñ äðóãîì, îáðàçóÿ ðåçóëüòèðóþùåå ïîëå.
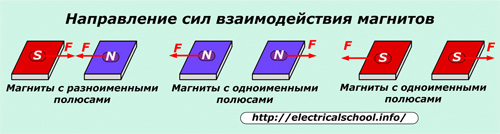
Ïðè ýòîì ìàãíèòû ñ ðàçíîèìåííûìè ïîëþñàìè (N – S) ïðèòÿãèâàþòñÿ äðóã ê äðóãó, à ñ îäíîèìåííûìè (N N, S – S) îòòàëêèâàþòñÿ. Ñèëû âçàèìîäåéñòâèÿ ìåæäó ïîëþñàìè çàâèñÿò îò ðàññòîÿíèÿ ìåæäó íèìè. ×åì áëèæå ñäâèíóòû ïîëþñà, òåì áîëüøåå óñèëèå âîçíèêàåò.
Îñíîâíûå õàðàêòåðèñòèêè ìàãíèòíîãî ïîëÿ
Ê íèì îòíîñÿò:
âåêòîð ìàãíèòíîé èíäóêöèè (Â);
ìàãíèòíûé ïîòîê (Ô);
ïîòîêîñöåïëåíèå (Ψ).
Èíòåíñèâíîñòü èëè ñèëó âîçäåéñòâèÿ ïîëÿ îöåíèâàþò âåëè÷èíîé âåêòîðà ìàãíèòíîé èíäóêöèè. Îíà îïðåäåëÿåòñÿ çíà÷åíèåì ñèëû «F», ñîçäàâàåìîé ïðîõîäÿùèì òîêîì «I» ïî ïðîâîäíèêó äëèíîé «l». Â=F/(I∙l)
Åäèíèöà èçìåðåíèÿ ìàãíèòíîé èíäóêöèè â ñèñòåìå ÑÈ Òåñëà (â çíàê ïàìÿòè îá ó÷åíîì ôèçèêå, êîòîðûé èññëåäîâàë ýòè ÿâëåíèÿ è îïèñàë èõ ìàòåìàòè÷åñêèìè ìåòîäàìè).  ðóññêîé òåõíè÷åñêîé ëèòåðàòóðå îíà îáîçíà÷àåòñÿ «Òë», à â ìåæäóíàðîäíîé äîêóìåíòàöèè ïðèíÿò ñèìâîë «Ò».
1 Òë ýòî èíäóêöèÿ òàêîãî îäíîðîäíîãî ìàãíèòíîãî ïîòîêà, êîòîðûé âîçäåéñòâóåò ñ ñèëîé â 1 íüþòîí íà êàæäûé ìåòð äëèíû ïðÿìîëèíåéíîãî ïðîâîäíèêà, ïåðïåíäèêóëÿðíî ðàñïîëîæåííîãî íàïðàâëåíèþ ïîëÿ, êîãäà ïî ýòîìó ïðîâîäíèêó ïðîõîäèò òîê 1 àìïåð.
1Òë=1∙Í/(À∙ì)
Íàïðàâëåíèå âåêòîðà Â îïðåäåëÿåòñÿ ïî ïðàâèëó ëåâîé ðóêè.
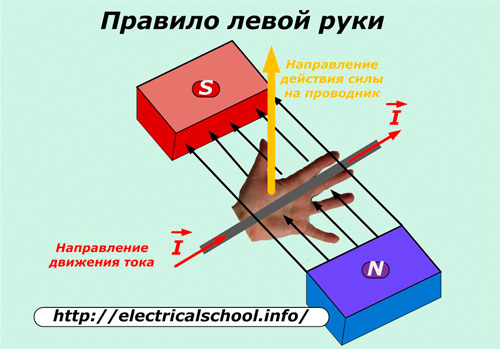
Åñëè ðàñïîëîæèòü ëàäîíü ëåâîé ðóêè â ìàãíèòíîì ïîëå òàê, ÷òîáû ñèëîâûå ëèíèè èç ñåâåðíîãî ïîëþñà âõîäèëè â ëàäîíü ïîä ïðÿìûì óãëîì, à ÷åòûðå ïàëüöà ðàñïîëîæèòü ïî íàïðàâëåíèþ òîêà â ïðîâîäíèêå, òî îòòîïûðåííûé áîëüøîé ïàëåö óêàæåò íàïðàâëåíèå äåéñòâèÿ ñèëû íà ýòîò ïðîâîäíèê.
 ñëó÷àå, êîãäà ïðîâîäíèê ñ ýëåêòðè÷åñêèì òîêîì ðàñïîëîæåí íå ïîä ïðÿìûì óãëîì ê ìàãíèòíûì ñèëîâûì ëèíèÿì, òî ñèëà, âîçäåéñòâóþùàÿ íà íåãî, áóäåò ïðîïîðöèîíàëüíà âåëè÷èíå ïðîòåêàþùåãî òîêà è ñîñòàâëÿþùåé ÷àñòè ïðîåêöèè äëèíû ïðîâîäíèêà ñ òîêîì íà ïëîñêîñòü, ðàñïîëîæåííóþ â ïåðïåíäèêóëÿðíîì íàïðàâëåíèè.
Ñèëà, âîçäåéñòâóþùàÿ íà ýëåêòðè÷åñêèé òîê, íå çàâèñèò îò ìàòåðèàëîâ, èç êîòîðûõ ñîçäàí ïðîâîäíèê è ïëîùàäè åãî ñå÷åíèÿ. Äàæå åñëè ýòîãî ïðîâîäíèêà âîîáùå íå áóäåò, à äâèæóùèåñÿ çàðÿäû ñòàíóò ïåðåìåùàòüñÿ â äðóãîé ñðåäå ìåæäó ìàãíèòíûìè ïîëþñàìè, òî ýòà ñèëà íèêàê íå èçìåíèòñÿ.
Åñëè âíóòðè ìàãíèòíîãî ïîëÿ âî âñåõ òî÷êàõ âåêòîð  èìååò îäèíàêîâîå íàïðàâëåíèå è âåëè÷èíó, òî òàêîå ïîëå ñ÷èòàþò ðàâíîìåðíûì.
Ëþáàÿ ñðåäà, îáëàäàþùàÿ ìàãíèòíûìè ñâîéñòâàìè, îêàçûâàåò âëèÿíèå íà çíà÷åíèå âåêòîðà èíäóêöèè Â.
Ìàãíèòíûé ïîòîê (Ô)
Åñëè ðàññìàòðèâàòü ïðîõîæäåíèå ìàãíèòíîé èíäóêöèè ÷åðåç îïðåäåëåííóþ ïëîùàäü S, òî îãðàíè÷åííàÿ åå ïðåäåëàìè èíäóêöèÿ áóäåò íàçûâàòüñÿ ìàãíèòíûì ïîòîêîì.
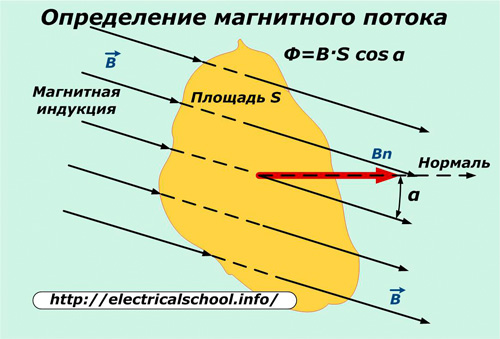
Êîãäà ïëîùàäü íàêëîíåíà ïîä êàêèì-òî óãëîì α ê íàïðàâëåíèþ ìàãíèòíîé èíäóêöèè, òî ìàãíèòíûé ïîòîê óìåíüøàåòñÿ íà âåëè÷èíó êîñèíóñà óãëà íàêëîíà ïëîùàäè. Ìàêñèìàëüíîå æå åãî çíà÷åíèå ñîçäàåòñÿ ïðè ïåðïåíäèêóëÿðíîì ðàñïîëîæåíèè ïëîùàäè ê åå ïðîíèçûâàþùåé èíäóêöèè. Ô=·S
Åäèíèöåé èçìåðåíèÿ ìàãíèòíîãî ïîòîêà ÿâëÿåòñÿ 1 âåáåð, îïðåäåëÿåìûé ïðîõîæäåíèåì èíäóêöèè â 1 òåñëó ÷åðåç ïëîùàäü â 1 ìåòð êâàäðàòíûé.
Ïîòîêîñöåïëåíèå
Ýòîò òåðìèí èñïîëüçóåòñÿ äëÿ ïîëó÷åíèÿ ñóììàðíîé âåëè÷èíû ìàãíèòíîãî ïîòîêà, ñîçäàâàåìîãî îò îïðåäåëåííîãî êîëè÷åñòâà ïðîâîäíèêîâ ñ òîêîì, ðàñïîëîæåííûõ ìåæäó ïîëþñàìè ìàãíèòà.
Äëÿ ñëó÷àÿ, êîãäà îäèí è òîò æå òîê I ïðîõîäèò ïî îáìîòêå êàòóøêè ñ ÷èñëîì âèòêîâ n, òî ïîëíûé (ñöåïëåííûé) ìàãíèòíûé ïîòîê îò âñåõ âèòêîâ íàçûâàþò ïîòîêîñöåïëåíèåì Ψ.
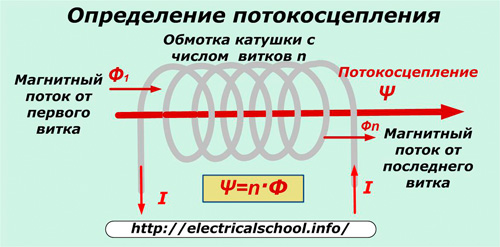
Ψ=n·Ô. Åäèíèöåé èçìåðåíèÿ ïîòîêîñöåïëåíèÿ ÿâëÿåòñÿ 1 âåáåð.
Êàê îáðàçóåòñÿ ìàãíèòíîå ïîëå îò ïåðåìåííîãî ýëåêòðè÷åñêîãî
Ýëåêòðîìàãíèòíîå ïîëå, âçàèìîäåéñòâóþùåå ñ ýëåêòðè÷åñêèìè çàðÿäàìè è òåëàìè, îáëàäàþùèìè ìàãíèòíûìè ìîìåíòàìè, ïðåäñòàâëÿåò ñîáîé ñîâîêóïíîñòü äâóõ ïîëåé:
ýëåêòðè÷åñêîãî;
ìàãíèòíîãî.
Îíè âçàèìîñâÿçàíû, ïðåäñòàâëÿþò ñîáîé ñîâîêóïíîñòü äðóã äðóãà è ïðè èçìåíåíèè â òå÷åíèå âðåìåíè îäíîãî ïðîèñõîäÿò îïðåäåëåííûå îòêëîíåíèÿ â äðóãîì. Ê ïðèìåðó, ïðè ñîçäàíèè ïåðåìåííîãî ñèíóñîèäàëüíîãî ýëåêòðè÷åñêîãî ïîëÿ â òðåõôàçíîì ãåíåðàòîðå îäíîâðåìåííî îáðàçóåòñÿ òàêîå æå ìàãíèòíîå ïîëå ñ õàðàêòåðèñòèêàìè àíàëîãè÷íûõ ÷åðåäóþùèõñÿ ãàðìîíèê.
Ìàãíèòíûå ñâîéñòâà âåùåñòâ
Ïî îòíîøåíèþ ê âçàèìîäåéñòâèþ ñ âíåøíèì ìàãíèòíûì ïîëåì âåùåñòâà ïîäðàçäåëÿþò íà:
àíòèôåððîìàãíåòèêè ñ óðàâíîâåøåííûìè ìàãíèòíûìè ìîìåíòàìè, áëàãîäàðÿ ÷åìó ñîçäàåòñÿ î÷åíü ìàëàÿ ñòåïåíü íàìàãíè÷åííîñòè òåëà;
äèàìàãíåòèêè ñî ñâîéñòâîì íàìàãíè÷èâàíèÿ âíóòðåííåãî ïîëÿ ïðîòèâ äåéñòâèÿ âíåøíåãî. Êîãäà æå âíåøíåå ïîëå îòñóòñòâóåò, òî ó íèõ ìàãíèòíûå ñâîéñòâà íå ïðîÿâëÿþòñÿ;
ïàðàìàãíåòèêè ñî ñâîéñòâàìè íàìàãíè÷èâàíèÿ âíóòðåííåãî ïîëÿ ïî íàïðàâëåíèþ äåéñòâèÿ âíåøíåãî, êîòîðûå îáëàäàþò ìàëîé ñòåïåíüþ ìàãíåòèçìà;
ôåððîìàãíåòèêè, îáëàäàþùèå ìàãíèòíûìè ñâîéñòâàìè áåç ïðèëîæåííîãî âíåøíåãî ïîëÿ ïðè òåìïåðàòóðàõ, ìåíüøèõ çíà÷åíèÿ òî÷êè Êþðè;
ôåððèìàãíåòèêè ñ íåóðàâíîâåøåííûìè ïî âåëè÷èíå è íàïðàâëåíèþ ìàãíèòíûìè ìîìåíòàìè.
Âñå ýòè ñâîéñòâà âåùåñòâ íàøëè ðàçíîîáðàçíîå ïðèìåíåíèå â ñîâðåìåííîé òåõíèêå.
Ìàãíèòíûå öåïè
Ýòèì òåðìèíîì íàçûâàþò ñîâîêóïíîñòü ðàçëè÷íûõ ìàãíèòíûõ ìàòåðèàëîâ, ïî êîòîðûì ïðîïóñêàþò ìàãíèòíûé ïîòîê. Îíè ÿâëÿþòñÿ àíàëîãîì ýëåêòðè÷åñêèõ öåïåé è îïèñûâàþòñÿ ñîîòâåòñòâóþùèìè ìàòåìàòè÷åñêèìè çàêîíàìè (ïîëíîãî òîêà, Îìà, Êèðõãîôà è äð). Ñìîòðèòå – Îñíîâíûå çàêîíû ýëåêòðîòåõíèêè.
Íà îñíîâå ðàñ÷åòîâ ìàãíèòíûõ öåïåé ðàáîòàþò âñå òðàíñôîðìàòîðû, èíäóêòèâíîñòè, ýëåêòðè÷åñêèå ìàøèíû è ìíîãèå äðóãèå óñòðîéñòâà.
Íàïðèìåð, ó ðàáîòàþùåãî ýëåêòðîìàãíèòà ìàãíèòíûé ïîòîê ïðîõîäèò ïî ìàãíèòîïðîâîäó èç ôåððîìàãíèòíûõ ñòàëåé è âîçäóõó ñ âûðàæåííûìè íå ôåððîìàãíèòíûìè ñâîéñòâàìè. Ñîâîêóïíîñòü ýòèõ ýëåìåíòîâ è ñîñòàâëÿåò ìàãíèòíóþ öåïü.
Áîëüøèíñòâî ýëåêòðè÷åñêèõ àïïàðàòîâ â ñâîåé êîíñòðóêöèè èìåþò ìàãíèòíûå öåïè. Ïîäðîáíåå ïðî ýòî ÷èòàéòå â ýòîé ñòàòüå – Ìàãíèòíûå öåïè ýëåêòðè÷åñêèõ àïïàðàòîâ
×èòàéòå òàêæå ïî ýòîé òåìå: Ïðèìåðû ðàñ÷åòîâ ìàãíèòíûõ öåïåé
Источник