Какое свойство лапласа отражает что умножение аргумента оригинала

Операторный метод берет начало со времени анализа бесконечно малых величин, когда были обнаружены определенные аналогии между дифференциально-интегральными и алгебраическими уравнениями. В XIX в. был опубликован ряд работ по операционному исчислению М.Е. Ващенко-Захарченко, О. Хэвисайда, Д. Карсона и др. Однако строгое обоснование операторный метод получил только в XX в. на базе общей теории функциональных преобразований.

В основе операторного метода расчета переходных процессов лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительного переменного t в область комплексного переменного р:

При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексного переменного на оператор р, что существенно упрощает расчет, так как сводит систему дифференциальных уравнений к системе алгебраических. В операторном методе отпадает необходимость определения постоянных интегрирования. Этими обстоятельствами объясняется широкое применение этого метода на практике.

Различают прямое и обратное преобразование Лапласа. Прямое преобразование Лапласа определяется уравнением.

где f(t) — функция действительного переменного t, определенная при t 0 (при t < 0; f(t) = 0) и удовлетворяющая условиям ограниченного роста:

где множитель М и показатель роста с0 — положительные действительные числа. На рис. 7.1 изображена область определения функции комплексного переменного F(p).

Обратное преобразование Лапласа определяют из решения (7.2):

Функция F(p), определяемая уравнением (7.2), носит название изображения по Лапласу, а функция f(t) в (7.4) — оригинала. Следовательно, оригинал и изображение представляют собой пару функций действительного (t) и комплексного (p) переменного, связанных преобразованием Лапласа. Для сокращенной записи преобразований (7.2), (7.4) используют следующую символику

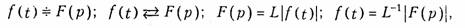
Какое свойство лапласа отражает что умножение аргумента оригинала

где L – оператор Лапласа. В дальнейшем для определенности будем использовать знак соответствия .

Рассмотрим основные свойства преобразований Лапласа.

Свойство линейности является следствием линейности преобразования Лапласа, его можно записать в форме

где ak — постоянные коэффициенты разложения. Свойство (7.5) легко доказать, если применить к левой части соотношения (7.5) прямое преобразование Лапласа (7.2).

Дифференцирование оригинала

При ненулевых начальных условиях: f(0–)¹ 0 дифференцирование оригинала соответствует следующему условию

Для доказательства (7.6) подставим f¢(t) в преобразование (7.2) в виде

Отсюда после интегрирования по частям получаем:

В случае нулевых начальных условий

Интегрирование оригинала

Доказательство осуществляется путем использования свойства дифференцирования оригинала (7.6), (7.7).

Изменение масштаба независимого переменного (теорема подобия)

где а — постоянный вещественный коэффициент. Свойство (7.9) легко доказывается путем замены независимой переменной t = atв прямом преобразовании Лапласа (7.2).

Смещение в области действительного переменного (теорема запаздывания)

Для доказательства (7.10) введем следующие обозначения:

Осуществим замену переменной t = t ± t0.

что и требовалось доказать.

Из соотношения (7.10) следует, что сдвиг оригинала по оси времени на t0 соответствует умножению изображения на .

Смещения в области комплексного переменного (теорема смещения)

Теорема (7.11) следует непосредственно из прямого преобразования Лапласа, если в (7.2) вместо f(t) подставить . Причем l может быть как действительной, так и комплексной величиной.

Дифференцирование и интегрирование оригинала по параметру (свойство коммутативности)

Для доказательства свойств (7.12), (7.13) достаточно продифференцировать или проинтегрировать прямое преобразование Лапласа (7.2) по параметру х.

Произведение изображений

Интегралы в (7.14) носят название свертки функций f1(t) и f2(t).

Дифференцирование изображения

Свойство (7.15) легко доказывается путем дифференцирования прямого преобразования Лапласа (7.2).

Интегрирование изображения

Данное свойство доказывается аналогично (7.15).

В заключение приведем предельные соотношения для оригинала и изображения:

Действительно, согласно свойства дифференцирования оригинала можно записать:

Учитывая, что , получаем:

Отсюда непосредственно следует соотношение (7.17). Аналогично доказывается равенство (7.18).

В качестве примера найдем изображение по Лапласу типовых сигналов. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используются различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательность прямоугольных импульсов и так далее. Особо важную роль в теоретических исследованиях электрических цепей играют испытательные сигналы в форме единичной функции 1(t) и единичной импульсной функции d(t) (функция Дирака).

Единичная функция

Единичная функция задается уравнением (рис. 7.2, а)

Изображение функции (7.19) будет равно:

Единичная импульсная функция (функция Дирака)

Эта функция называется еще d-функцией; она задается уравнением

Функция Дирака является физически нереализуемой математической абстракцией, однако обладает рядом интересных свойств и играет очень важную роль в теоретических исследованиях. Формально она может быть получена, например, предельным переходом (при t ® 0) единичного импульса (см. рис. 7.2, б), площадь которого равна единице:

Одним из интересных свойств функции d(t) является ее фильтрующее свойство, определяемое равенством (рис. 7.3):

Найдем изображение единичной импульсной функции в форме изображения разности двух единичных функций величины 1(t), сдвинутых друг относительно друга на t (рис. 7.4). Для этих функций с учетом теоремы запаздывания имеем:

Для результирующего изображения с учетом свойства линейности получим

Устремив t ® 0, найдем изображение единичной импульсной функции (d-функции):

Экспоненциальный сигнал при t > 0:

т. е.

Подобным же образом можно найти изображение по Лапласу других функций, удовлетворяющих условию (7.3). В литературе имеются специальные справочники, в которых приведены оригиналы и изображения широкого класса функций. В табл. 7.1 приведены оригиналы и их изображения наиболее часто встречающихся в теории электрических цепей функций.

Источник

Содержание

Обнаружили ошибку?
Выделите ее мышью
и нажмите
ctrl+enter

Преобразование Лапласа как разложение сигнала по системе затухающих комплексных экспонент

Ранее мы рассмотрели преобразование Фурье сигнала xleft( t right) :

equation 1

(1)

где Xleft( omega right) — спектральная плотность сигнала xleft( t right) ,
mathcal{F}[ bullet ] и $mathcal{F}^{-1}[ bullet ]$ — операторы
прямого и обратного преобразования Фурье соответственно.

Условием существования преобразования Фурье является абсолютная интегрируемость исходного сигнала сигнала xleft( t right) , т.е. сходимость интеграла:

equation 2

(2)

При рассмотрении преобразования Фурье предполагается, что время измеряется от минус бесконечности до плюс бесконечности. Кроме того (2) сужает класс сигналов, для которых существует преобразование Фурье.

С другой стороны, все физические процессы имеют начало, поэтому мы можем считать, что исходный сигнал xleft( t right) определён на положительном интервале времени, т.е xleft( t right)=0 , при tle 0 .

Для того, чтобы предотвратить расхождение интеграла (2) умножим входной сигнал xleft( t right) на {{exp }({-sigma t})} , где sigma — вещественная величина.
Рассмотрим преобразование Фурье ${{X}_{sigma }}left( omega right)$ полученного сигнала:

equation 3

(3)

Очевидно, ${{X}_{sigma }}left( omega right)$ зависит от параметра sigma . Тогда ${{X}_{sigma }}left( omega right)$ можно трактовать как функцию двух вещественных переменных Xleft( sigma ,omega right) или как функцию одной комплексной переменной Xleft( sigma +jomega right) . Обозначив s = sigma +jomega получим:

equation 4

(4)

Выражение (4) представляет собой разложение xleft( t right) по системе затухающих комплексных экспонент exp big(left( sigma +jomega right)tbig) , которое носит название преобразования Лапласа, где mathcal{L}[ bullet ] — оператор преобразования.

Исходный сигнал x(t) называют оригиналом, а X(s) — образом, или изображением оригинала.

Обратное преобразование Лапласа

Обратное преобразование Фурье (3) от ${X}_{sigma }(omega)$ имеет вид:

equation 5

(5)

Умножим левую и правую части (5) на {{exp }({sigma t})} , получим:

equation 6

(6)

Учтём, что ${{X}_{sigma }}left( omega right)=Xleft( sigma +jomega right)=Xleft( s right)$ , изменим переменную интегрирования с omega на :

equation 7

(7)

При этом верхний и нижний пределы интегрирования равны:

equation 8

(8)

Окончательно (6) с учётом 7 и (8):

equation 9

(9)

Выражение (9) определяет обратное преобразование Лапласа, которое обозначается оператором $mathcal{L}^{-1}[ bullet ]$ .

Некоторые свойства преобразования Лапласа

Свойство линейности

Пусть сигнал xleft( t right)=aleft( t right)+bleft( t right) . Тогда преобразование Лапласа X(s) :

equation 10

(10)

Следствием (10) является умножение на константу:

equation 11

(11)

Свойство подобия (масштабирование по аргументу)

Пусть сигнал xleft( t right) имеет образ Xleft( s right) . Тогда изображение масштабированного во времени сигнала xleft( at right) равно:

equation 12

(12)

Аналогично можно показать , что масштабирование образа по аргументу Xleft( as right) приводит к оригиналу вида:

equation 13

(13)

Преобразование Лапласа задержанного сигнала

Рассмотрим преобразование Лапласа сигнала xleft( t-Delta t right) , задержанного во времени на положительную величину Delta t>0 .

equation 14

(14)

Важно отметить, что (14) справедливо, если задержка Delta t положительна, как это показано на рисунке 1.

Пример положительной и отрицательной задержки сигнала

Рисунок 1. Пример положительной и отрицательной
задержки сигнала

Если же задержка отрицательна, то :

equation 15

(15)

Аналогичное свойство смещения образа:

equation 16

(16)

Таким образом, смещение образа Xleft( s+a right) на произвольное комплексное приводит к умножению сигнала на {{exp }({-at})} .

Свойство дифференцирования оригинала и образа

Пусть дан сигнал xleft( t right) и его преобразование Лапласа равно Xleft( s right) . Рассмотрим преобразование Лапласа производной сигнала ${x}'left( t right) = frac{dx(t)}{dt}$ :

equation 17

(17)

Применяя правило интегрирования по частям :

equation 18

(18)

где xleft( 0 right) — значение сигнала при t=0 . Если функция xleft( t right) при t=0 имеет разрыв, то вместо необходимо брать правый предел xleft( +0 right) :

equation 19

(19)

при стремлении к нулю справа.

Таким образом, использование аппарата преобразования Лапласа позволяет заменить дифференцирование умножением образа на переменную . Это важнейшее свойство дало возможность перейти от дифференциальных уравнений при анализе цепей переменного тока к алгебраическим и использовать всю мощь аппарата операционного исчисления и теории функций комплексного переменного для синтеза и анализа электрических цепей.

Приведем также выражение для обратного преобразования Лапласа производной образа .
Пусть Xleft( s right) — образ сигнала xleft( t right) . Тогда

equation 20

(20)

где ${{X}^{left( n right)}}left( s right)$ — производная -го порядка образа Xleft( s right) .

Свойство интегрирования оригинала и образа

Пусть сигнал yleft(t right) есть результат интегрирования сигнала xleft(t right) :

equation 21

(21)

Рассмотрим преобразование Лапласа Y(s) от yleft( t right) :

equation 22

(22)

Изменим порядок интегрирования и получим:

equation 23

(23)

Получили еще одно важнейшее свойство: образ интеграла от входного сигнала xleft( t right) равен образу Xleft( s right) этого сигнала, деленного на переменную . Это свойство также позволяет заменить интегральные уравнения и системы на алгебраические.

Преобразование Лапласа свертки двух сигналов

Пусть сигнал xleft( t right) представляет собой свертку двух сигналов aleft( t right) и hleft( t right) , определяемую соотношением:

equation 24

(24)

Важность интеграла свертки (24) в том, что им описывается результат прохождения сигнала aleft( t right) через линейный фильтр с импульсной характеристикой hleft( t right) .

Обратим внимание, что пределы интегрирования от 0 до обусловлены тем, что a(t) и h(t) отличны от нуля только для положительных значений переменной .

Рассмотрим преобразование Лапласа Xleft( s right) сигнала xleft( t right) :

equation 25

(25)

Поменяем местами операции интегрирования, и учтем свойство временного сдвига (14):

equation 26

(26)

Таким образом, интеграл свертки заменяется произведением образов Aleft( s right) входного сигнала aleft( t right) и образа Hleft( s right) импульсной характеристики фильтра hleft( t right) .

Данное свойство также является очень важным, поскольку анализ многокаскадных фильтров заменяется простым произведением образов импульсных характеристик этих фильтров.

Выводы

В данном разделе мы рассмотрели преобразование Лапласа и его некоторые свойства.

Аппарат операционного исчисления является основным инструментом анализа
электрических цепей переменного тока, ввиду возможности замены операций
дифференцирования и интегрирования алгебраическим умножением и делением
на переменную .

Подробнее использование преобразования Лапласа для анализа цепей
переменного тока будет рассмотрено в следующем разделе.

Список литературы

[1]

Будак, Б.М., Фомин, С.В.
Кратные интегралы и ряды.
Москва, Наука, 1965, 608 c.

[2]

Дёч, Г.
Руководство по практическому применению преобразования Лапласа.
Москва, Наука, 1965, 288 c.

[3]

Ильин, В.А., Позняк Э.Г.
Основы математического анализа.
Москва, Наука, 1965, 572 c.

[4]

Свешников, А.Г., Тихонов, А.Н.
Теория функций комплексной переменной.
Москва, Наука, 1967, 304 с.

Последнее изменение страницы: 14.11.2020 (11:21:07)

Страница создана Latex to HTML translator ver. 5.20.11.14

Источник

1°. Общие сведения о преобразовании Лапласа: оригинал и изображение

Функцией-оригиналом называется комплекснозначная функция действительного переменного , удовлетворяющая следующим условиям:

1) , если ;

2) функция интегрируема на любом конечном интервале оси ;

3) с возрастанием модуль функции растет не быстрее некоторой показательной функции, т. е. существуют числа и такие, что для всех имеем

(1)

Изображением функции-оригинала по Лапласу называется функция комплексного переменного , определяемая равенством

(2)

при . Условие 3 обеспечивает существование интеграла (2).

Преобразование (2), ставящее в соответствие оригиналу его изображение , называется преобразованием Лапласа. При этом пишут .

Свойства преобразования Лапласа

Всюду в дальнейшем считаем, что

(3)

I. Свойство линейности. Для любых комплексных постоянных и

(4)

II. Теорема подобия. Для любого постоянного

(5)

III. Дифференцирование оригинала. Если есть оригинал, то

(6)

Обобщение: если раз непрерывно дифференцируема на и если есть оригинал, то

(7)

IV. Дифференцирование изображения равносильно умножению оригинала на “минус аргумент”, т.е.

(8)

Обобщение:

(9)

V. Интегрирование оригинала сводится к делению изображения на

(10)

VI. Интегрирование изображения равносильно делению на оригинала:

(11)

(предполагаем, что интеграл сходится).

VII. Теорема запаздывания. Для любого положительного числа

(12)

VIII. Теорема смещения (умножение оригинала на показательную функцию). Для любого комплексного числа

(13)

IX. Теорема умножения (Э. Борель). Произведение двух изображений и также является изображением, причем

(14)

Интеграл в правой части (14) называется сверткой функций и и обозначается символом

Теорема XI утверждает, что умножение изображений равносильно свертыванию оригиналов, т.е.

(15)

Отыскание оригиналов дробно-рациональных изображений

Для нахождения оригинала по известному изображению , где есть правильная рациональная дробь, применяют следующие приемы.

1) Эту дробь разлагают на сумму простейших дробей и находят для каждой из них оригинал, пользуясь свойствами I–IX преобразования Лапласа.

2) Находят полюсы этой дроби и их кратности . Тогда оригиналом для будет функция

(16)

где сумма берется по всем полюсам функции .

В случае, если все полюсы функции простые, т.е. , последняя формула упрощается и принимает вид

(17)

Пример 1. Найти оригинал функции , если

Решение. Первый способ. Представим в виде суммы простейших дробей

и найдем неопределенные коэффициенты . Имеем

Полагая в последнем равенстве последовательно , получаем

откуда ; значит,

Находя оригиналы для каждой из простейших дробей и пользуясь свойствам линейности, получаем

Второй способ. Найдем полюсы функции . Они совпадают с нулями знаменателя . Таким образом, изображение имеет четыре простых полюса . Пользуясь формулой (17), получаем оригинал

Пример 2. Найти оригинал , если .

Решение. Данная дробь имеет полюс кратности и полюс кратности . Пользуясь формулой (16), получаем оригинал

2°. Решение задачи Коши для линейных дифференциальных уравнений с постоянными коэффициентами

Пусть требуется найти решение дифференциального уравнения второго порядка с постоянными коэффициентами

(18)

удовлетворяющее начальным условиям

(19)

Будем считать, что функция и решение вместе с его производньь ми до второго порядка включительно являются функциями-оригиналами. Пусть . По правилу дифференцирования оригиналов с учетом (2) имеем

Применяя к обеим частям (1) преобразование Лапласа и пользуясь свойством линейности преобразования, получаем операторное уравнение

(20)

Решая уравнение (20), найдем операторное решение

Находя оригинал для , получаем решение уравнения (18), удовлетворяющее начальным условиям (19).

Аналогично можно решить любое уравнение n-го порядка с постоянными коэффициентами и с начальными условиями при .

Пример 3. Решить дифференциальное уравнение операторным методом

(21)

(22)

Решение. Пусть , тогда по правилу дифференцирования оригинала имеем

Известно, что поэтому, переходя отданной задачи (21)–(22) к операторному уравнению, будем иметь

откуда следовательно,

Легко видеть, что функция удовлетворяет данному уравнению и начальному условию задачи.

Пример 4. Решить уравнение .

Решение. Так как и по условию , то операторное уравнение будет иметь вид

Отсюда находим операторное решение

Разлагаем правую часть на элементарные дроби:

Переходя к оригиналам, получаем искомое решение .

Пример 5. Решить уравнение .

Решение. Так как и по условию , то операторное уравнение будет иметь вид

и, следовательно, операторное решение

Разложим правую часть на элементарные дроби:

Переходя к оригиналам, получим решение поставленной задачи

3°. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами

Пусть требуется найти решение системы двух уравнений с постоянными коэффициентами

(23)

удовлетворяющее начальным условиям

(24)

Будем предполагать, что функции , а также и являются функциями-оригиналами.

Пусть

По правилу дифференцирования оригиналов с учетом (24) имеем

Применяя к обеим частям каждого из уравнений системы (23) преобразование Лапласа, получим операторную систему

Эта система является линейной алгебраической системой двух уравнений с двумя неизвестными и . Решая ее, мы найдем и , а затем, переходя к оригиналам, получим решение системы (23), удовлетворяющее начальным условиям (24). Аналогично решаются линейные системы вида

Пример 6. Найти решение системы дифференциальных уравнений операторным методом

удовлетворяющее начальному условию .

Решение. Так как и , то операторная система будет иметь вид

Решая систему, получаем

Разлагаем дроби, стоящие в правых частях, на элементарные:

Переходя к оригиналам, получим искомое решение

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник