Какое свойство лапласа отражает
Операторный метод берет начало со времени анализа бесконечно малых величин, когда были обнаружены определенные аналогии между дифференциально-интегральными и алгебраическими уравнениями. В XIX в. был опубликован ряд работ по операционному исчислению М.Е. Ващенко-Захарченко, О. Хэвисайда, Д. Карсона и др. Однако строгое обоснование операторный метод получил только в XX в. на базе общей теории функциональных преобразований.
В основе операторного метода расчета переходных процессов лежит преобразование Лапласа, которое позволяет перенести решение из области функций действительного переменного t в область комплексного переменного р:
При этом операции дифференцирования и интегрирования функций времени заменяются соответствующими операциями умножения и деления функций комплексного переменного на оператор р, что существенно упрощает расчет, так как сводит систему дифференциальных уравнений к системе алгебраических. В операторном методе отпадает необходимость определения постоянных интегрирования. Этими обстоятельствами объясняется широкое применение этого метода на практике.
Различают прямое и обратное преобразование Лапласа. Прямое преобразование Лапласа определяется уравнением.
где f(t) — функция действительного переменного t, определенная при t 0 (при t < 0; f(t) = 0) и удовлетворяющая условиям ограниченного роста:
где множитель М и показатель роста с0 — положительные действительные числа. На рис. 7.1 изображена область определения функции комплексного переменного F(p).
Обратное преобразование Лапласа определяют из решения (7.2):
Функция F(p), определяемая уравнением (7.2), носит название изображения по Лапласу, а функция f(t) в (7.4) — оригинала. Следовательно, оригинал и изображение представляют собой пару функций действительного (t) и комплексного (p) переменного, связанных преобразованием Лапласа. Для сокращенной записи преобразований (7.2), (7.4) используют следующую символику
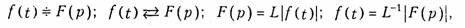
где L – оператор Лапласа. В дальнейшем для определенности будем использовать знак соответствия .
Рассмотрим основные свойства преобразований Лапласа.
Свойство линейности является следствием линейности преобразования Лапласа, его можно записать в форме
где ak — постоянные коэффициенты разложения. Свойство (7.5) легко доказать, если применить к левой части соотношения (7.5) прямое преобразование Лапласа (7.2).
Дифференцирование оригинала
При ненулевых начальных условиях: f(0–)¹ 0 дифференцирование оригинала соответствует следующему условию
Для доказательства (7.6) подставим f¢(t) в преобразование (7.2) в виде
Отсюда после интегрирования по частям получаем:
В случае нулевых начальных условий
Интегрирование оригинала
Доказательство осуществляется путем использования свойства дифференцирования оригинала (7.6), (7.7).
Изменение масштаба независимого переменного (теорема подобия)
где а — постоянный вещественный коэффициент. Свойство (7.9) легко доказывается путем замены независимой переменной t = atв прямом преобразовании Лапласа (7.2).
Смещение в области действительного переменного (теорема запаздывания)
Для доказательства (7.10) введем следующие обозначения:
Осуществим замену переменной t = t ± t0.
что и требовалось доказать.
Из соотношения (7.10) следует, что сдвиг оригинала по оси времени на t0 соответствует умножению изображения на .
Смещения в области комплексного переменного (теорема смещения)
Теорема (7.11) следует непосредственно из прямого преобразования Лапласа, если в (7.2) вместо f(t) подставить . Причем l может быть как действительной, так и комплексной величиной.
Дифференцирование и интегрирование оригинала по параметру (свойство коммутативности)
Для доказательства свойств (7.12), (7.13) достаточно продифференцировать или проинтегрировать прямое преобразование Лапласа (7.2) по параметру х.
Произведение изображений
Интегралы в (7.14) носят название свертки функций f1(t) и f2(t).
Дифференцирование изображения
Свойство (7.15) легко доказывается путем дифференцирования прямого преобразования Лапласа (7.2).
Интегрирование изображения
Данное свойство доказывается аналогично (7.15).
В заключение приведем предельные соотношения для оригинала и изображения:
Действительно, согласно свойства дифференцирования оригинала можно записать:
Учитывая, что , получаем:
Отсюда непосредственно следует соотношение (7.17). Аналогично доказывается равенство (7.18).
В качестве примера найдем изображение по Лапласу типовых сигналов. Для теоретических и экспериментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используются различные типы сигналов: гармонические колебания, уровни постоянных напряжений, последовательность прямоугольных импульсов и так далее. Особо важную роль в теоретических исследованиях электрических цепей играют испытательные сигналы в форме единичной функции 1(t) и единичной импульсной функции d(t) (функция Дирака).
Единичная функция
Единичная функция задается уравнением (рис. 7.2, а)
Изображение функции (7.19) будет равно:
Единичная импульсная функция (функция Дирака)
Эта функция называется еще d-функцией; она задается уравнением
Функция Дирака является физически нереализуемой математической абстракцией, однако обладает рядом интересных свойств и играет очень важную роль в теоретических исследованиях. Формально она может быть получена, например, предельным переходом (при t ® 0) единичного импульса (см. рис. 7.2, б), площадь которого равна единице:
Одним из интересных свойств функции d(t) является ее фильтрующее свойство, определяемое равенством (рис. 7.3):
Найдем изображение единичной импульсной функции в форме изображения разности двух единичных функций величины 1(t), сдвинутых друг относительно друга на t (рис. 7.4). Для этих функций с учетом теоремы запаздывания имеем:
Для результирующего изображения с учетом свойства линейности получим
Устремив t ® 0, найдем изображение единичной импульсной функции (d-функции):
Экспоненциальный сигнал при t > 0:
т. е.
Подобным же образом можно найти изображение по Лапласу других функций, удовлетворяющих условию (7.3). В литературе имеются специальные справочники, в которых приведены оригиналы и изображения широкого класса функций. В табл. 7.1 приведены оригиналы и их изображения наиболее часто встречающихся в теории электрических цепей функций.
Источник
Преобразование Лапласа
Оригинал. Показатель роста. Изображение. Свойства преобразования Лапласа. Дифференцирование и интегрирование оригинала. Дифференцирование и интегрирование изображения. Теоремы запаздывания и смещения. Свертка функций. Теорема Бореля. Формула Дюамеля. Операционный метод решения дифференциальных уравнений
Операционное исчисление – это раздел функционального анализа, в котором рассматривается специальный операционный метод решения различных математических задач. Основу этого метода составляет идея интегрального преобразования, переводящего функцию действительного переменного t в функцию комплексного переменного р.
Пусть функция обладает следующими свойствами:
при t <0
при t >0, где M >0 и – некоторые действительные постоянные.
3) На любом конечном отрезке [а, b] положительной полуоси Ot функция f(t) удовлетворяет условиям Дирихле, т. е.:
а) ограничена;
б) либо непрерывна, либо имеет лишь конечное число точек конечного разрыва
в) имеет конечное число экстремумов.
Такие функции в операционном исчислении называются оригиналами.
Пусть — комплексный параметр, причем . При сформулированных условиях интеграл
сходится и является функцией от р:
Этот интеграл называется интегралом Лапласа, а определяемая им функция комплексного аргумента р называется преобразованием Лапласа от функции , лапласовым изображением ,или просто, изображением . Тот факт, что функция является изображением оригинала , обозначают так:
В дальнейшем изложении запись будет означать, что
Пример 1. Найти изображение оригинала
Решение.
~ ~ ~
Свойства преобразования Лапласа
1. Однородность. При умножении оригинала на комплексное число изображение также умножается на это число:
Пример 2 . Найти изображение оригинала
Решение. Используя результат примера 1 и свойство однородности, получаем:
Пример 3. Найти изображение оригинала
Решение. По определению
~
~ ~
~ ~ ~
~ ~
~ ~
Пример 4. Найти изображение оригинала
Решение. По определению
~
2. Аддитивность. Изображение суммы оригиналов равно сумме изображений этих оригиналов:
Пример 5. Найти изображение оригинала
Решение. Из теории функций комплексного переменного известно, что
где – мнимая единица. Следовательно, в силу свойств однородности и аддитивности, а также с учетом примера 4, получаем
3. Подобие. Если , то справедлива формула:
Пример 6. Найти изображение оригинала
Решение. Воспользуемся результатом примера 5 и свойством подобия:
4. Дифференцирование оригинала. Если и является оригиналом, то справедлива формула дифференцирования оригинала:
где
Пример 7. Найти изображение оригинала
Решение. Воспользуемся результатом примера 5 и свойством формулой дифференцирования оригинала:
В общем случае, если и являются оригиналами, то справедлива формула:
где
5. Интегрирование оригинала. Если , то справедлива формула:
Пример 8. Найти изображение оригинала
Решение. Воспользуемся примером 1 и свойством интегрирования оригинала:
6. Дифференцирование изображения. Если , то справедлива формула:
Пример 9. Найти изображение оригинала
Решение. Воспользуемся примером 8 и свойством дифференцирования изображения:
Таким образом,
7. Интегрирование изображения. Если и является оригиналом, то справедлива формула:
Пример 10. Найти изображение оригинала
Решение. Из примеров 1, 4 следует, что
Значит, по свойству интегрирования изображения
~ ~
~
Итак,
8. Запаздывание. Если , то справедлива формула:
Пример 11. Найти изображение оригинала
Решение. Из примеров 1, 4 следует, что
9. Смещение. Если , то справедлива формула:
Пример 12. Найти изображение оригинала
Решение. Из примера 6 следует, что
По условию задачи . Следовательно, используя свойство смещения, получаем:
10. Предельные соотношения. Если и является оригиналом, то справедливы формулы:
Свертка функций
Сверткой функций и называется функция
Свойства операции свертывания:
1. коммутативность
2. ассоциативность
3. дистрибутивность
Теорема Бореля. Если и , то
Другими словами, произведение изображений является изображением свертки их оригиналов
Пример 13. Найти свертку оригиналов
Решение. Изображения данных оригиналов таковы:
На основании теоремы Бореля получаем
Теорема Дюамеля. Если оригиналы и непрерывно дифференцируемы на полупрямой [0, ∞), то справедлива формула:
Пример 14. Найти оригинал по изображению
Решение. Из примера 4 следует, что
Пусть , , . Тогда по формуле Дюамеля
Из примера 13 вытекает, что
Таблица основных изображений
Источник
ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Основные положения операторного метода
Сущность метода
Расчёт переходных процессов классическим методом сводится к решению дифференциальных уравнений. При этом основные трудности решения заключаются в определении постоянных интегрирования. По мере усложнения электрической цепи и повышения порядка дифференциального уравнения эти трудности увеличиваются. Избежать этого позволяет операторный метод интегрирования линейных дифференциальных уравнений.
В электротехнику операторный метод в конце прошлого столетия ввёл О. Хевисайд. В настоящее время этот метод находит широкое применение в различных областях: энергетике, радиотехнике, связи и т.д.
Сущность метода заключается в следующем.
Заданную функцию действительного переменного (например, времени) преобразуют в функцию комплексного переменного , где . При этом исходную функцию называют оригиналом, а его изображением.
Дифференциальные уравнения для оригиналов, согласно правилам преобразования функций, их производных и интегралов, преобразуют в операторные алгебраические уравнения для изображений. Полученные операторные уравнения решают относительно функции комплексного переменного . Затем осуществляют переход от функции комплексного переменного к оригиналу .
Таким образом, сложные математические операции решения дифференциальных уравнений заменяются решением простых алгебраических уравнений, записанных в операторной форме. Операторный метод можно сравнить с логарифмированием, где сначала от чисел переходят к их логарифмам, потом производят относительно простые действия над логарифмами, соответствующие действиям над числами, а затем от найденного логарифма возвращаются к некоторому числу. При использовании комплексного метода расчёта установившегося режима в цепях синусоидального тока мы также применяем изображение синусоидальной функции функцией комплексной переменной.
Для преобразования функции вещественной переменной в функцию комплексной переменной пользуются преобразованием Лапласа.
Преобразование Лапласа
Пусть задана некоторая функция времени , удовлетворяющая условиям Дирихле:
1) за любой конечный промежуток времени имеет конечное число разрывов первого рода (нигде не превращается в бесконечность);
2) возрастает не быстрее показательной функции (существует постоянное число , такое, что для всех t ).
Практически все функции, описывающие переходные процессы в реальных линейных электрических цепях, удовлетворяют этим условиям.
Преобразование вида
| (9.1) |
носит название преобразования Лапласа.
Оказывается, что если функция удовлетворяет перечисленным условиям Дирихле, то несобственный интеграл сходится, т.е. имеет конечное значение. В выражении (9.1): е – основание натурального логарифма; ( ) – новая переменная. Интеграл (9.1) используется для перехода от оригинала к изображению , причём сопоставление этих функций получается однозначным.
Существует обратное функциональное преобразование, дающее возможность определить оригинал по его изображению . Такое преобразование, носящее название обратного преобразования Лапласа, имеет вид
(9.2)
Следует отметить, что между изображением и оригиналом нет равенства, а есть только соответствие. Это важное положение подчёркивается условной записью, связывающей изображение с оригиналом. В литературе встречаются следующие виды символов, связывающие оригинал с его изображением:
; ; ; и др.
Соответствие между оригиналом и изображением будем в дальнейшем записывать в таком виде: или .
Кроме преобразования Лапласа используется также преобразование Карсона-Хевисайда:
.
Преимущество преобразования по Карсону состоит в том, что размерности оригинала и его изображения одинаковы, что не имеет места в преобразовании по Лапласу. Тем не менее, будем пользоваться преобразованием Лапласа, так как оно тесно связано с преобразованием Фурье и может трактоваться как обобщение преобразования Фурье.
Пример 9.1
Найти операторное изображение по Лапласу функции
Решение
Используя (9.1) получаем
.
Если , то получаем Если и , то получаем Поскольку , то и
Пример 9.2
Найти операторное изображение по Лапласу для функции .
Решение
Операторное изображение функции имеет вид
.
Используя интегрирование по частям:
и обозначив и , имеем , ,
.
При подстановке верхнего предела в первое слагаемое получается неопределенность, раскрываемая по правилу Лопиталя:
.
Таким образом,
.
Изображения встречающихся в электротехнике функций уже рассчитаны. Они сведены в таблицы, имеющиеся в справочниках и специальной литературе. В таблице 9.1 приведены оригиналы и изображения наиболее часто встречающихся функций.
Таблица 9.1
Основные свойства преобразования Лапласа
1. При умножении оригинала на постоянную величину на ту же постоянную величину умножается и изображение:
2. Если оригинал представлен суммой функций, то изображение этой суммы равно сумме изображений этих функций:
| (9.3) |
Доказательство выражения (9.3) вытекает непосредственно из свойств определённого интеграла
.
3. Изображение производной.
Пусть дана некоторая функция и известно её изображение F(p). Тогда изображение Ф(p) производной этой функции :
.
Интегрируя по частям при и ( ; ) и используя условие существования интеграла Лапласа: , получаем
.
Итак, изображение производной имеет вид
| (9.4) |
где – значение функции при . Согласно (9.4) вычисление изображения производной функции при нулевых начальных условиях ( ) соответствует умножению изображения функции на оператор .
Используя формулу (9.4), можно найти изображение второй производной оригинала:
или
Повторяя эти вычисления раз, получим изображение производной оригинала го порядка:
| (9.5) |
где
.
В выражении (9.5) и все её производные до включительно непрерывны.
Если начальные значения функции и всех её производных равны нулю, то изображение производных, определяемых уравнением (9.5), упрощается и находится по изображению исходной функции простым умножением на оператор в степени, соответствующей порядку производной:
4. Изображение интеграла.
Пусть дана некоторая функция и известно её изображение . Необходимо найти изображение интеграла от этой функции
Так как и =0, то Учитывая, что изображение функции равно получаем Таким образом, окончательно имеем:
| (9.6) |
Согласно (9.6) интегрированию функции в пределах от 0 до t соответствует деление изображения этой функции на оператор p. При многократном интегрировании в пределах от 0 до t можно получить общее выражение:
| (9.7) |
где n – любое целое число.
Приведём также некоторые теоремы, которые могут быть использованы при расчётах электротехнических задач.
5. Теорема подобия.
Изменение масштаба независимого переменного осуществляется согласно выражению
6. Теорема запаздывания.
Смещение в области действительного переменного на время равносильно умножению изображения на :
.
7. Теорема смещения.
Смещение в области комплексной переменной p на величину равносильно умножению оригинала на показательную функцию :
.
8. Теорема свертывания.
Теорема свертывания в области действительной переменной име-
ет вид:
Умножение в области действительного переменного соответствует свёртыванию в области комплексного переменного (следствие теоремы свёртывания)
.
Источник
