Какое свойство конденсатора характеризует электрическая емкость
Электроемкость конденсатора – это характеристика двух проводников, которые находятся в теле устройства. Эта величина не зависит от номинала заряда и величины его напряжения. На нее влияют геометрия и габариты самых проводников, их месторасположения относительно друг друга, а также технических характеристик диэлектрика, который находится между ними и его свойств.
Большая часть этих радиодеталей имеют плоский вид. В качестве проводников используются пластины из алюминия или фольги из него. В качестве диэлектрика выступает бумага, пропитанная парафином или слюда. Они так и называются – слюдяные, бумажные или воздушные.
В данной статьи рассмотрены все вопросы по расчеты электроемкости конденсаторов. В качестве бонуса. в конце статьи читатель найдет видеоролик по теме и интересный материал, расчету электроемкости.

Расчет электроемкости.
Электроемкость
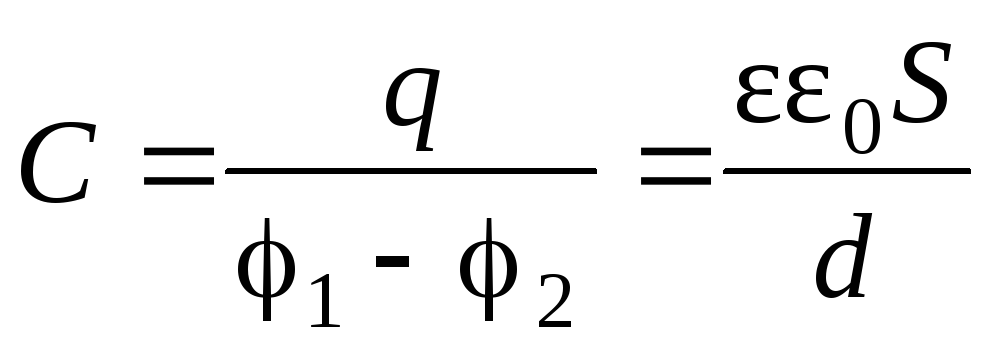 Электроемкость — это скалярная величина, характеризующая способность проводника накапливать электрический заряд.
Электроемкость — это скалярная величина, характеризующая способность проводника накапливать электрический заряд.
Электроемкость:
- не зависит от q и U;
- зависит от геометрических размеров проводника, их формы, взаимного расположения, электрических свойств среды между проводниками.
Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу:
единица измерения емкости в СИ: Ф (фарад)
Конденсатор обладает свойством накапливать и сохранять электрическую энергию. Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. обкладками конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок.
Материал по теме: Как проверить конденсатор
Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками. Основные слагаемые электроемкости представлены на рисунке ниже:
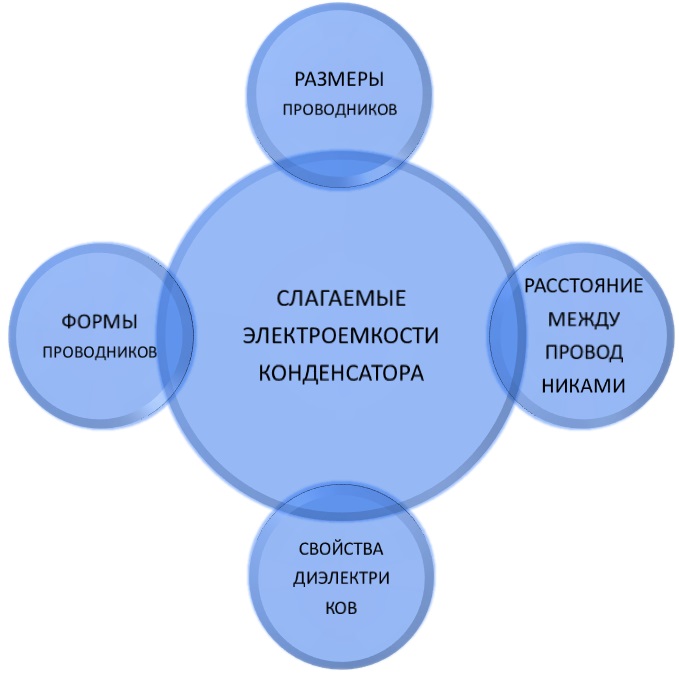
Основные слагаемые электроемкости.
Обозначение на электрических схемах:
- Все электрическое поле сосредоточено внутри конденсатора.
- Заряд конденсатора — это абсолютное значение заряда одной из обкладок конденсатора.
Виды конденсаторов:
- по виду диэлектрика — воздушные, слюдяные, керамические, электролитические.
- по форме обкладок — плоские, сферические.
- по величине емкости — постоянные, переменные (подстроечные).
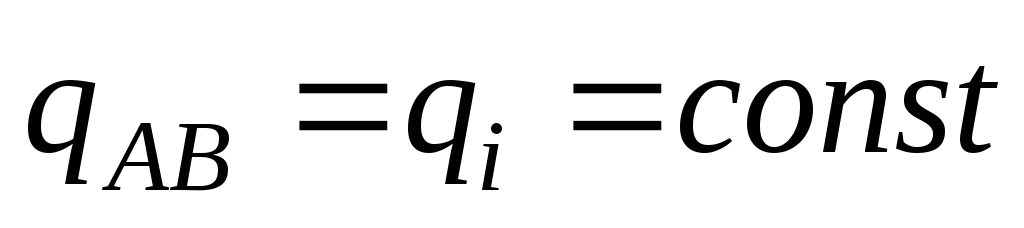
Электроемкость.
Электроемкость плоского конденсатора
где S — площадь пластины (обкладки) конденсатора
- d — расстояние между пластинами
- εо — электрическая постоянная
ε — диэлектрическая проницаемость диэлектрика
Конденсатор — это система заряженных тел обладает энергией.
Энергия любого конденсатора:
где С — емкость конденсатора, (Ф) W— энергия (Дж)
q — заряд конденсатора, (Кл)
U — напряжение на обкладках конденсатора, (В
Энергия равна работе, которую совершит электрическое поле при сближении пластин конденсатора вплотную, или работе по разделению положительных и отрицательных зарядов необходимой при зарядке конденсатора. Конденсаторы применяются для накопления электрической энергии и использования ее при быстром разряде (фотовспышка), для разделения цепей постоянного и переменного тока, в радиотехнике: колебательный контур, выпрямитель и других радиоэлектронных устройствах.
Электрическая емкость конденсатора
Дальнейшие опыты с распределением электричества по поверхности наэлектризованного проводника, проводимые Кулоном и другими естествоиспытателями, позволили установить, что равномерное распределение электричества имеет место только на правильной шаровой поверхности. В общем случае заряд неравномерен и зависит от формы проводника, будучи больше в местах большей кривизны. Отношение количества электричества на части поверхности проводника к величине этой поверхности назвали плотностью (толщиной) электрического слоя. Экспериментально было установлено, что электрическая плотность и электрическая сила особенно велики в местах поверхности, имеющих наибольшую кривизну, особенно на остриях.
Интересный материал для ознакомления: что такое вариасторы.
Величину, характеризующую зависимость потенциала наэлектризованного проводника от его размеров, формы и окружающей среды, называют электроемкостью проводника и обозначают буквой С. Электроемкость проводника измеряется количеством электричества, необходимым для повышения потенциала этого проводника на единицу:
С = q/ϕ.
 За единицу электроемкости в системе СИ принимается 1 фарада (1 Ф). Фарадой называется электроемкость проводника, которому для повышения его потенциала на один вольт нужно сообщить один кулон электричества. Электроемкостью, равной 1 Ф, обладал бы шар радиусом 9·10 6 км, что в 23 раза больше расстояния от Земли до Луны. Если проводник соединить с источником электричества определенного потенциала, то проводник получит электрический заряд, зависящий от емкости проводника. Его емкость, а, следовательно, и количество электричества, которым он заряжается, увеличиваются, если приблизить к нему второй проводник, соединенный с землей.
За единицу электроемкости в системе СИ принимается 1 фарада (1 Ф). Фарадой называется электроемкость проводника, которому для повышения его потенциала на один вольт нужно сообщить один кулон электричества. Электроемкостью, равной 1 Ф, обладал бы шар радиусом 9·10 6 км, что в 23 раза больше расстояния от Земли до Луны. Если проводник соединить с источником электричества определенного потенциала, то проводник получит электрический заряд, зависящий от емкости проводника. Его емкость, а, следовательно, и количество электричества, которым он заряжается, увеличиваются, если приблизить к нему второй проводник, соединенный с землей.
Конструкция, состоящая из двух проводников, разделенных изолятором, с электрическим полем между ними, все силовые линии которого начинаются на одном проводнике, а заканчиваются на другом, была названа электрическим конденсатором. При этом оба проводника называются обкладками, а изолирующая прокладка – диэлектриком. Процесс накопления зарядов на обкладках конденсатора называется его зарядкой. При зарядке на обеих обкладках накапливаются равные по величине и противоположные по знаку заряды.
Поскольку электрическое поле заряженного конденсатора сосредоточено в пространстве между его обкладками, то электроемкость конденсатора не зависит от окружающих тел. Электроемкость конденсатора измеряется отношением количества электричества на одной из обкладок к разности потенциалов между обкладками:
С = q/ U.
1 Ф – электроемкость такого конденсатора, который может быть заряжен количеством электричества, равным 1 Кл, до разности потенциалов между обкладками, равной 1 В. Например, электрическая емкость плоского конденсатора в системе СИ определяется по соотношению:
С =εε 0 S/ d, где ε – диэлектрическая проницаемость материала, находящегося между обкладками конденсатора; ε 0 – диэлектрическая проницаемость вакуума; S – величина площади поверхности пластины (меньшей, если они не равны); d – расстояние между пластинами.
Если обкладки заряженного конденсатора соединить проводником, то заряды будут переходить с одной обкладки на другую и нейтрализуют друг друга. Этот процесс называется разрядкой конденсатора. Каждый конденсатор рассчитан на определенное напряжение. Если напряжение между обкладками станет слишком большим, то разрядка может произойти и непосредственно через диэлектрик (без соединительного проводника), т.е. получится пробой диэлектрика.
Пробитый конденсатор к дальнейшему употреблению не пригоден. Для получения электроемкости нужной величины конденсаторы соединяют в батарею. На практике встречается как параллельное, так и последовательное соединение конденсаторов.
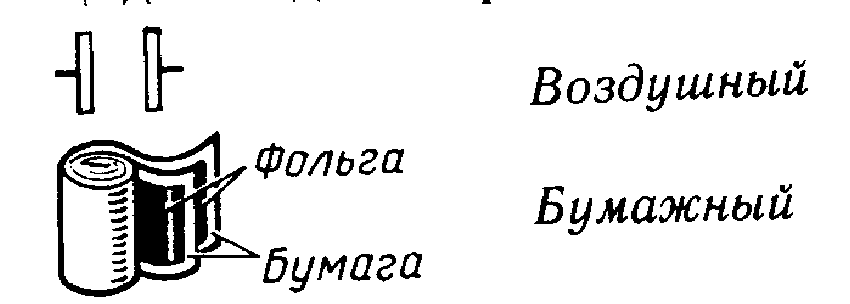
Строение конденсатора.
Единицы измерения
Физическая величина, определяемая отношением заряда q одной из пластин конденсатора к напряжению между обкладками конденсатора, называется электроемкостью конденсатора:
При неизменном расположении пластин электроемкость конденсатора является постоянной величиной при любом заряде на пластинах.
Единица электроемкости в международной системе – фарад (Ф). Электроемкостью 1 Ф обладает такой конденсатор, напряжение между обкладками которого равно 1 В при сообщении обкладкам разноименных зарядов по 1 Кл. . В практике широко используются дольные единицы электроемкости – микрофарад (мкФ), нанофарад (нФ) и пикофарад (пФ):
- 1 мкФ = 10-6Ф;
- 1 нФ = 10-9Ф;
- 1 пФ = 10-12Ф.
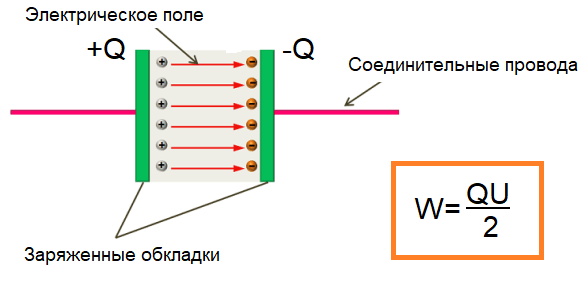 Электроемкость конденсатора прямо пропорциональна площади обкладок и обратно пропорциональна расстоянию между обкладками. При введении диэлектрика между обкладками конденсатора его электроемкость увеличивается в e раз. Если двум изолированным друг от друга проводникам сообщить заряды q1 и q2, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников.
Электроемкость конденсатора прямо пропорциональна площади обкладок и обратно пропорциональна расстоянию между обкладками. При введении диэлектрика между обкладками конденсатора его электроемкость увеличивается в e раз. Если двум изолированным друг от друга проводникам сообщить заряды q1 и q2, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников.
Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой U. Наибольший практический интерес представляет случай, когда заряды проводников одинаковы по модулю и противоположны по знаку: q1 = – q2 = q. В этом случае можно ввести понятие электрической емкости.
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними. Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства.
Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками. Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.
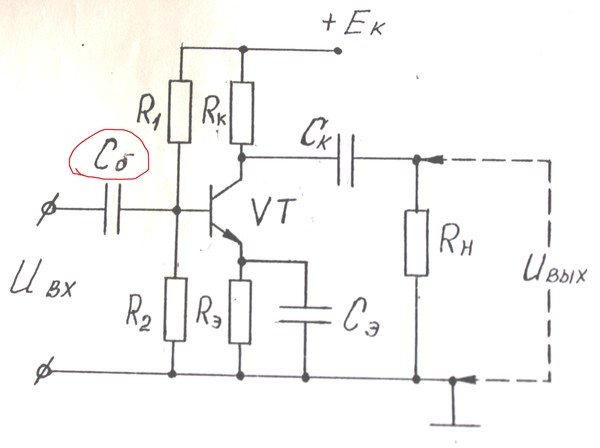 Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами (рисунок 1); однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния.
Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами (рисунок 1); однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния.
В целом ряде задач можно приближенно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками (рисунок 2). Но в других задачах пренебрежение полем рассеяния может привести к грубым ошибкам, так как при этом нарушается потенциальный характер электрического поля.
Согласно принципу суперпозиции, напряженность поля, создаваемого обеими пластинами, равна сумме напряженностей и полей каждой из пластин. Вне пластин вектора и направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q/S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Примерами конденсаторов с другой конфигурацией обкладок могут служить сферический и цилиндрический конденсаторы.
Электроемкость – характеристика проводника, количественная мера его способности удерживать электрический заряд. В электростатическом поле все точки поверхности проводника имеют один и тот же потенциал.
Потенциал φ (отсчитываемый от нулевого уровня на бесконечности) пропорционален заряду q проводника, т.е. отношение q к φ не зависит от q. Это позволяет ввести понятие электроемкости. С уединенного проводника, которая равна отношению заряда проводника к потенциалу:
С = q/ φ
Таким образом, чем больше электроемкость, тем больший заряд может накопить проводник при данном φ. Электроемкость определяется геометрическими размерами проводника, его формой и электрическими свойства окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. В частности, электроемкость проводящего шара в вакууме равна его радиусу. Наличие вблизи проводника других тел изменяет его электроемкость, так как потенциал проводника зависит и от электрических полей, создаваемых зарядами, наведенными в окружающих телах вследствие электростатической индукции.
В системе ед. СГСЭ электроемкость измеряется в сантиметрах, в СИ – в фарадах: 1Ф = 9*1011 см.
Понятие электроемкости относится также к системе проводников, в частности двух проводников, разделённых тонким слоем диэлектрика, – электрическому конденсатору. Электроемкость конденсатора (взаимная ёмкость его обкладок)
С = q/ (φ1 – φ2),
где q – заряд одной из обкладок (заряды обкладок по абсолютной величине равны), φ1 – φ2 – разность потенциалов между обкладками. Электроемкость конденсатора практически не зависит от наличия окружающих тел и может достигать очень большой величины при малых геометрических размерах конденсаторов.
Заключение
Более подробно об электроемкости конденсаторов можно узнать прочитав материал: “Электроемкость: как рассчитать”. Если у вас остались вопросы, можно задать их в комментариях на сайте. Также в нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессионалов.
Чтобы подписаться на группу, вам необходимо будет перейти по следующей ссылке: https://vк.coм/еlеctroinfonеt. В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию:
www.melon.narod.ru
www.energetika.in.ua
www.kaf-fiz-1586.narod.ru
www.heuristic.sul
www.kaplio.ru
www.lektsii.com
www.kopilkaurokov.ru
Следующая
ТеорияЭлектрическая цепь и ее элементы
Источник
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 декабря 2019;
проверки требуют 2 правки.
Электри́ческая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками[1].
В Международной системе единиц (СИ) ёмкость измеряется в фарадах, в системе СГС — в сантиметрах.
Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид
где — заряд, — потенциал проводника.
Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара (или сферы) радиуса R равна (в системе СИ):
где ε0 — электрическая постоянная, равная 8,854⋅10−12Ф/м, εr — относительная диэлектрическая проницаемость.
Вывод формулы
Известно, что
Так как , то подставив сюда найденный , получим, что
Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком или вакуумом, — к конденсатору. В этом случае ёмкость (взаимная ёмкость) этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:
где S — площадь одной обкладки (подразумевается, что обкладки одинаковы), d — расстояние между обкладками, εr — относительная диэлектрическая проницаемость среды между обкладками.
Электрическая ёмкость некоторых систем[править | править код]
Вычисление электрической ёмкости системы требует решение Уравнения Лапласа ∇2φ = 0 с постоянным потенциалом φ на поверхности проводников.
Это тривиально в случаях с высокой симметрией. Нет никакого решения в терминах элементарных функций в более сложных случаях.
В квазидвумерных случаях аналитические функции отображают одну ситуацию на другую, электрическая ёмкость не изменяется при таких отображениях. См. также Отображение Шварца — Кристоффеля.
Эластанс[править | править код]
Величина обратная ёмкости называется эластанс (эластичность). Единицей эластичности является дараф (daraf), но он не определён в системе физических единиц измерений СИ[10].
См. также[править | править код]
- Квантовая ёмкость
Примечания[править | править код]
- ↑ Шакирзянов Ф. Н. Ёмкость электрическая // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2. — С. 28—29. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ 1 2 Jackson, J. D. Classical Electrodynamics (неопр.). — Wiley, 1975. — С. 80.
- ↑ Binns; Lawrenson. Analysis and computation of electric and magnetic field problems (англ.). — Pergamon Press (англ.)русск., 1973. — ISBN 978-0-08-016638-4.
- ↑ 1 2 Maxwell, J. C. A Treatise on Electricity and Magnetism (неопр.). — Dover, 1873. — С. 266 ff. — ISBN 0-486-60637-6.
- ↑ Rawlins, A. D. Note on the Capacitance of Two Closely Separated Spheres (англ.) // IMA Journal of Applied Mathematics (англ.)русск. : journal. — 1985. — Vol. 34, no. 1. — P. 119—120. — doi:10.1093/imamat/34.1.119.
- ↑ Jackson, J. D. Classical Electrodynamics (неопр.). — Wiley, 1975. — С. 128, problem 3.3.
- ↑ Maxwell, J. C. On the electrical capacity of a long narrow cylinder and of a disk of sensible thickness (англ.) // Proc. London Math. Soc. : journal. — 1878. — Vol. IX. — P. 94—101. — doi:10.1112/plms/s1-9.1.94.
- ↑ Vainshtein, L. A. Static boundary problems for a hollow cylinder of finite length. III Approximate formulas (англ.) // Zh. Tekh. Fiz. : journal. — 1962. — Vol. 32. — P. 1165—1173.
- ↑ Jackson, J. D. Charge density on thin straight wire, revisited (неопр.) // Am. J. Phys. — 2000. — Т. 68, № 9. — С. 789—799. — doi:10.1119/1.1302908. — Bibcode: 2000AmJPh..68..789J.
- ↑ Тензорный анализ сетей, 1978, с. 509.
Литература[править | править код]
- Боргман И. И.,. Электроёмкость // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Савельев И.В. Глава X. Движение заряженных частиц. // Курс общей физики. — 3. — М.: Наука. Гл. ред. физ.-мат. лит., 1988. — Т. 2. — С. 87—88. — 496 с. — 220 000 экз.
- Г. Крон. Тензорный анализ сетей. — Москва: Сов. радио, 1978. — 720 с.
Источник
Что такое электроемкость проводников
Если у нас есть два проводника, изолированных друг от друга, которым мы сообщаем некоторые заряды (обозначим их соответственно q1 и q2), то между ними возникнет определенная разность потенциалов. Ее величина будет зависеть от формы проводников, а также от исходных величин зарядов. Обозначим такую разность Δφ. Если мы говорим о разности, возникающей в электрическом поле между двумя точками, то ее обычно обозначают U.
В рамках темы данной статьи нам больше всего интересна такая разность потенциалов между проводниками, когда их заряды противоположны по знаку, но равны друг другу по модулю. В таком случае мы можем ввести новое понятие – электрическая емкость (электроемкость).
Определение 1
Электрической емкостью системы, состоящей из двух проводников, называется отношение заряда одного проводника (q) к разности потенциалов между этими двумя проводниками.
В виде формулы это записывается так: C=q∆φ=qU.
Для измерения электрической емкости применяется единица, называемая фарад. Она обозначается буквой Ф.
1Φ=1 Кл1 В.
Конфигурации и размеры проводников, а также свойства диэлектрика определяют величину электроемкости заданной системы. Наибольший интерес для нас представляют проводники особой формы, называемые конденсаторами.
Определение 2
Конденсатор – это проводник, конфигурация которого позволяет локализовать (сосредотачивать) электрическое поле в одной выделенной части пространства. Проводники, составляющие конденсатор, называются обкладками.
Определение 3
Если мы возьмем две плоские пластины из проводящего материала, расположим их на небольшом расстоянии друг от друга и проложим между ними слой диэлектрика, то мы получим простейший конденсатор, называемый плоским. При его работе электрическое поле будет располагаться преимущественно в промежутке между пластинами, но небольшая часть этого поля будет рассеиваться вокруг них.
Определение 4
Часть электрического поля вблизи конденсатора называется полем рассеяния.
Иногда в задачах мы можем не учитывать его и работать только с той частью электрического поля, которое расположено между обкладками. Однако пренебрегать полем рассеяния допустимо далеко не всегда, поскольку это может привести к ошибочным расчетам из-за нарушения потенциального характера электрического поля.
Рисунок 1.6.1. Электрическое поле в плоском конденсаторе.
Рисунок 1.6.2. Электрическое поле конденсатора без учета поля рассеяния, не обладающее потенциальностью.
Модуль напряженности электрического поля, которое создает каждая обкладка в плоском конденсаторе, выражается соотношением следующего вида:
E1=σ2ε0.
Исходя из принципа суперпозиции, можно утверждать, что напряженность E→ поля, которое создают обе пластины конденсатора, будет равна сумме напряженностей E+→ и E-→ полей каждой пластины, то есть E→=E+→+E-→.
Векторы напряженностей обеих пластин во внутренней части конденсатора будут параллельны друг другу. Значит, мы можем выразить модуль напряженности их суммарного поля в виде формулы E=2E1=σε0.
Как рассчитать электроемкость конденсатора
Вне пластин векторы напряженности будут направлены в противоположные друг от друга стороны, значит, E будет равно нулю. Если мы обозначим заряд каждой обкладки как q, а ее площадь как S, то соотношение qS даст нам представление о поверхностной плотности. Умножив E на расстояние между обкладками (d), мы получим разность потенциалов между пластинами в однородном электрическом поле. Теперь возьмем оба этих соотношения и выведем из них формулу, по которой может быть рассчитана электрическая емкость конденсатора.
C=q∆φ=σ·SE·d=ε0Sd.
Определение 5
Электрическая емкость плоского конденсатора – величина, обратно пропорциональная расстоянию между обкладками и прямо пропорциональная их площади.
Заполнение пространства между проводниками диэлектрическим материалом может увеличить электроемкость плоского конденсатора в число раз, кратное undefined.
Определение 6
Введем обозначение емкости в виде буквы С и запишем это в виде формулы:
C=εε0Sd.
Данная формула называется формулой электроемкости плоского конденсатора.
Конденсаторы бывают не только плоскими. Возможны и другие конфигурации, также обладающие специфическими свойствами.
Определение 7
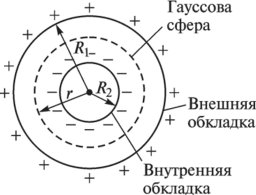
Сферическим конденсатором называется система из 2-х концентрических сфер, сделанных из проводящего материала, радиусы которых равны R1 и R2 соответственно.
Определение 8
Цилиндрическим конденсатором называется системы из двух проводников цилиндрической формы, длина которых равна L, а радиусы R1 и R2.
Обозначим проницаемость диэлектрического материала как ε и запишем формулы, по которым можно найти электрическую емкость конденсаторов:
- C=4πε0εR1R2R2-R1(сферический конденсатор),
- C=2πε0εLlnR2R1(цилиндрический конденсатор).
Как рассчитать электроемкость батареи конденсаторов
Определение 9
Если мы соединим несколько проводников между собой, то мы получим конструкцию, называемую батареей.
Способы соединения могут быть разными. Если соединение будет параллельным, то напряжение всех конденсаторов в системе будет одинаково: U1=U2 =U, а заряды можно найти по формулам q1=С1U и q2=C2U. При таком соединении вся система может считаться одним конденсатором, электроемкость которого равна C, заряд – q=q1+q2, а напряжение – U. В виде формулы это выглядит так:
С=q1+q2U или C=C1+C2
Определение 10
Если в батарее конденсаторов элементы соединены параллельно, то для нахождения общей электроемкости нам нужно сложить емкости ее отдельных элементов.
Рисунок 1.6.3. Конденсаторы, соединенные параллельно. C=C1+C2
Рисунок 1.6.4. Конденсаторы, соединенные последовательно: 1C=1C1+1C2
Если же батарея состоит из двух последовательно соединенных конденсаторов, то заряды обоих будут одинаковы: q1=q2=q. Найти их напряжения можно так: U1=qC1 и U2=qC2. Такую систему тоже можно считать одним конденсатором, заряд которого равен q, а напряжение U=U1+U2.
C=qU1+U2 или 1C=1C1+1C2
Определение 11
Если конденсаторы в батарее соединены последовательно, то для нахождения общей электроемкости нам нужно сложить величины, обратные емкостям каждого из них.
Справедливость обеих формул, приведенных выше, не зависит от количества конденсаторов в батарее.
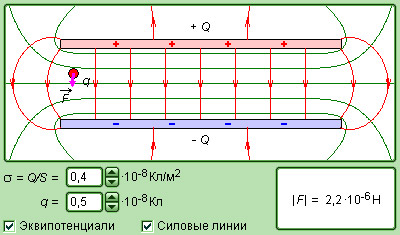
Рисунок 1.6.5. Смоделированное электрическое поле плоского конденсатора.
Источник
