Какое свойство электрического поля положено в основу принципа суперпозиции
Одна из задач, которые ставит электростатика перед собой – это оценка параметров поля при заданном стационарном распределении зарядов в пространстве. И принцип суперпозиции является одним из вариантов решения такой задачи.
Принцип суперпозиции
Предположим наличие трех точечных зарядов, находящихся во взаимодействии друг с другом. При помощи эксперимента возможно осуществить измерение сил, действующих на каждый из зарядов. Для нахождения суммарной силы, с которой на один заряд действуют два других заряда, нужно силы воздействия каждого из этих двух сложить по правилу параллелограмма. При этом логичен вопрос: равны ли друг другу измеряемая сила, которая действует на каждый из зарядов, и совокупность сил со стороны двух иных зарядов, если силы рассчитаны по закону Кулона. Результаты исследований демонстрируют положительный ответ на этот вопрос: действительно, измеряемая сила равна сумме вычисляемых сил согласно закону Кулона со стороны других зарядов. Данное заключение записывается в виде совокупности утверждений и носит название принципа суперпозиции.
Определение 1
Принцип суперпозиции:
- сила взаимодействия двух точечных зарядов не изменяется, если присутствуют другие заряды;
- сила, действующая на точечный заряд со стороны двух других точечных зарядов, равна сумме сил, действующих на него со стороны каждого из точечных зарядов при отсутствии другого.
Принцип суперпозиции полей заряда является одним из фундаментов изучения такого явления, как электричество: значимость его сопоставима с важностью закона Кулона.
В случае, когда речь идет о множестве зарядов N (т.е. нескольких источников поля), суммарную силу, которую испытывает на себе пробный заряд q, можно определить по формуле:
F→=∑i=1NFia→,
где Fia→ является силой, с которой влияет на заряд q зарядqi, если прочий N-1 заряд отсутствует.
При помощи принципа суперпозиции с использованием закона взаимодействия между точечными зарядами существует возможность определить силу взаимодействия между зарядами, присутствующими на теле конечных размеров. С этой целью каждый заряд разбивается на малые заряды dq (будем считать их точечными), которые затем берутся попарно; вычисляется сила взаимодействия и в заключение осуществляется векторное сложение полученных сил.
Полевая трактовка принципа суперпозиции
Определение 2
Полевая трактовка: напряженность поля двух точечных зарядов есть сумма напряженностей, создаваемым каждым из зарядов при отсутствии другого.
Для общих случаев принцип суперпозиции относительно напряженностей имеет следующую запись:
E→=∑Ei→,
где Ei→=14πε0qiεri3ri→ является напряженностью i-го точечного заряда, ri→ – радиусом вектора, проложенного от i-го заряда в некоторую точку пространства. Указанная формула говорит нам о том, что напряженность поля любого числа точечных зарядов есть сумма напряженностей полей каждого из точечных зарядов, если другие отсутствуют.
Инженерная практика подтверждает соблюдение принципа суперпозиции даже для очень больших напряженностей полей.
Значимым размером напряженности обладают поля в атомах и ядрах (порядка 1011-1017 Вм), но и в этом случае применялся принцип суперпозиции для расчетов энергетических уровней. При этом наблюдалось совпадение результатов расчетов с данными экспериментов с большой точностью.
Все же следует также заметить, что в случае очень малых расстояний (порядка ~10-15 м) и экстремально сильных полей принцип суперпозиции, вероятно, не выполняется.
Пример 1
Например, на поверхности тяжелых ядер при напряженности порядка ~1022 Вм принцип суперпозиции выполняется, а при напряженности 1020 Вм возникают квантово-механические нелинейности взаимодействия.
Когда распределение заряда является непрерывным (т.е. отсутствует необходимость учета дискретности), совокупная напряженность поля задается формулой:
E→=∫dE→.
В этой записи интегрирование проводится по области распределения зарядов:
- при распределении зарядов по линии (τ=dqdl – линейная плотность распределения заряда) интегрирование проводится по линии;
- при распределении зарядов по поверхности (σ=dqdS – поверхностная плотность распределения) интегрирование проводится по поверхности;
- при объемном распределении заряда (ρ=dqdV – объемная плотность распределения) интегрирование проводится по объему.
Принцип суперпозиции дает возможность находить E→ для любой точки пространства при известном типе пространственного распределения заряда.
Примеры применения принципа суперпозиции
Пример 2
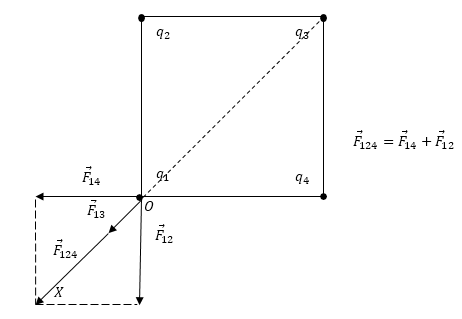
Заданы одинаковые точечные заряды q, расположенные в вершинах квадрата со стороной a. Необходимо определить, какая сила воздействует на каждый заряд со стороны других трех зарядов.
Решение
На рисунке 1 проиллюстрируем силы, влияющие на любой из заданных зарядов в вершинах квадрата. Поскольку условием задано, что заряды одинаковы, для иллюстрации возможно выбрать любой из них. Сделаем запись суммирующей силы, влияющей на заряд q1:
F→=F12→+F14→+F13→.
Силы F12→ и F14→ являются равными по модулю, определим их так:
F13→=kq22a2.

Рисунок 1
Теперь зададим направление оси ОХ (рисунок 1), спроектируем уравнение F→=F12→+F14→+F13→, подставим в него полученные выше модули сил и тогда:
F=2kq2a2·22+kq22a2=kq2a222+12.
Ответ: сила, оказывающее воздействие на каждый из заданных зарядов, находящихся в вершинах квадрата, равна F=kq2a222+12.
Пример 3
Задан электрический заряд, распределенный равномерно вдоль тонкой нити (с линейной плотностью τ). Необходимо записать выражение, определяющее напряженность поля на расстоянии a от конца нити вдоль ее продолжения. Длина нити – l.
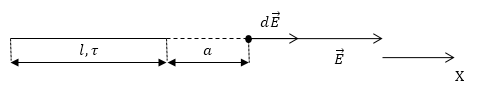
Рисунок 2
Решение
Первым нашим шагом будет выделение на нити точечного заряда dq. Составим для него, в соответствии с законом Кулона, запись, выражающую напряженность электростатического поля:
dE→=kdqr3r→.
В заданной точке все векторы напряженности имеют одинаковую направленность вдоль оси ОХ, тогда:
dEx=kdqr2=dE.
Условием задачи дано, что заряд имеет равномерное распределение вдоль нити с заданной плотностью, и запишем следующее:
dq=τdr.
Подставим эту запись в записанное ранее выражение напряженности электростатического поля, проинтегрируем и получим:
E=k∫al+aτdrr2=kτ-1ral+a=kτla(l+a).
Ответ: напряженность поля в указанной точке будет определяться по формуле E=kτla(l+a).
Источник
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 июля 2019;
проверки требуют 18 правок.
Эта статья — о суперпозиции в линейных системах. О суперпозиции квантовых состояний см. квантовая суперпозиция; о других значениях см. суперпозиция.
Принцип суперпозиции — один из самых общих законов во многих разделах физики. В самой простой формулировке принцип суперпозиции гласит:
- Результат воздействия на частицу нескольких внешних сил есть векторная сумма воздействия этих сил.
- Любое сложное движение можно разделить на два и более простых.
Наиболее известен принцип суперпозиции в электростатике, в которой он утверждает, что напряженность электростатического поля, создаваемого в данной точке системой зарядов, есть векторная сумма напряженности полей отдельных зарядов.
Принцип суперпозиции может принимать и иные формулировки, которые полностью эквивалентны приведённой выше:
- Энергия взаимодействия всех частиц в многочастичной системе есть просто сумма энергий парных взаимодействий между всеми возможными парами частиц. В системе нет многочастичных взаимодействий.
- Уравнения, описывающие поведение многочастичной системы, являются линейными по количеству частиц.
Именно линейность фундаментальной теории в рассматриваемой области физики есть причина возникновения в ней принципа суперпозиции.
Принцип суперпозиции в электродинамике[править | править код]
Принцип суперпозиции является следствием, прямо вытекающим из рассматриваемой теории, а вовсе не постулатом, вносимым в теорию a priori. Так, например, в электростатике принцип суперпозиции есть следствие того факта, что уравнения Максвелла в вакууме линейны. Именно из этого следует, что потенциальную энергию электростатического взаимодействия системы зарядов можно легко сосчитать, вычислив потенциальную энергию каждой пары зарядов.
Другим следствием линейности уравнений Максвелла является тот факт, что лучи света не рассеиваются и вообще никак не взаимодействуют друг с другом. Этот закон можно условно назвать принципом суперпозиции в оптике.
Подчеркнём, что электродинамический принцип суперпозиции не есть незыблемый закон Природы, а является всего лишь следствием линейности уравнений Максвелла, то есть уравнений классической электродинамики. Поэтому, когда мы выходим за пределы применимости классической электродинамики, вполне стоит ожидать нарушение принципа суперпозиции.
Примеры нарушения электродинамического принципа суперпозиции[править | править код]
Если рассматривается электродинамика не в вакууме, а в какой-либо среде, то принцип суперпозиции может нарушаться. Так, например, если поляризуемость или намагниченность среды нелинейно зависят от приложенного поля, это приводит к нелинейным поправкам в уравнениях Максвелла. Прямым следствием этого является нарушение принципа суперпозиции в такой нелинейной среде.
В некоторых случаях эти нелинейности невелики, и принцип суперпозиции с некоторой степенью приближения может выполняться. В других случаях нарушение принципа суперпозиции велико и может приводить к принципиально новым явлениям. Так, например, два луча света, распространяющиеся в нелинейной среде, могут изменять траекторию друг друга. Более того, даже один луч света в нелинейной среде может воздействовать сам на себя и изменять свои характеристики. Многочисленные эффекты такого типа изучает нелинейная оптика.
Принцип суперпозиции нарушается также в вакууме при учёте квантовых явлений.
В квантовой электродинамике фотон может на некоторое время превратиться в электрон-позитронную пару, которая уже может взаимодействовать с другими фотонами. Эффективно это приводит к тому, что фотоны могут взаимодействовать друг с другом. Такого типа процессы (рассеяние света на свете (англ.)русск. и другие процессы нелинейной электродинамики) наблюдались экспериментально. [1]
Отсутствие принципа суперпозиции в нелинейных теориях[править | править код]
Тот факт, что уравнения классической электродинамики линейны, является скорее исключением, чем правилом. Многие фундаментальные теории современной физики являются нелинейными. Например, квантовая хромодинамика — фундаментальная теория сильных взаимодействий — является разновидностью теории Янга — Миллса, которая нелинейна по построению. Это приводит к сильнейшему нарушению принципа суперпозиции даже в классических (неквантованных) решениях уравнений Янга — Миллса.
Другим известным примером нелинейной теории является общая теория относительности. В ней также не выполняется принцип суперпозиции. Например, гравитационное поле Солнца влияет не только на Землю и Луну, но также и на гравитационное взаимодействие между Землёй и Луной. Вне воздействия гравитационного поля Солнца гравитационное взаимодействие между Землёй и Луной отличалось бы от наблюдаемого. Впрочем, в слабых гравитационных полях эффекты нелинейности слабы, и для повседневных задач приближённый принцип суперпозиции выполняется с высокой точностью.
Наконец, принцип суперпозиции не выполняется, когда речь идёт о взаимодействии атомов и молекул. Это можно пояснить следующим образом. Рассмотрим два атома, связанных общим электронным облаком. Поднесем теперь точно такой же третий атом. Он как бы оттянет на себя часть связывающего атомы электронного облака, и в результате энергия связи между первоначальными атомами изменится.
Нарушение принципа суперпозиции во взаимодействиях атомов в немалой степени приводит к тому удивительному разнообразию физических и химических свойств веществ и материалов, которое так трудно предсказать из общих принципов молекулярной динамики.
Принцип суперпозиции в электротехнике[править | править код]
Электрический ток в каждой ветви линейной электрической цепи равен алгебраической сумме токов, вызываемых каждым из источников ЭДС цепи в отдельности.
Принцип суперпозиции в теории автоматического управления[править | править код]
В автоматике принцип суперпозиции необходим для решения задач анализа линейных динамических систем. Основываясь на принципе суперпозиции и знания переходных или импульсных характеристик, можно получить реакцию линейной динамической системы на произвольное воздействие.
Любое физически реализуемое воздействие может быть заменено суммой ступенчатых воздействий. Тогда реакцию системы можно представить как сумму реакций на отдельные ступенчатые воздействия.
В результате математических преображений получается математическая модель динамики линейной системы в виде интеграла свертки двух функций. Математическая модель в виде интегралов свертки позволяет по известной переходной или импульсной характеристике рассчитать реакцию динамической системы на заданное входное воздействие. Это будет представлять собой необходимый переходный процесс.
Если заданы лишь переходные характеристики отдельных звеньев, то более эффективным и относительно простым решением задач синтеза и анализа линейных систем могут быть получены с помощью интегральных преобразований Лапласа и Фурье. [2]
Примечания[править | править код]
Источник
Тема:
Законы электродинамики
Тела, имеющие определенный объем и линейные размеры, всегда занимают часть пространства, в котором не могут находиться другие тела без изменения тех или иных характеристик. Там, где находится камень, не может находиться ни другой камень, ни металлический шар, ни любой другой вещественный объект.
Характерной особенностью электрического поля является то, что, в отличие от вещества, в одной точке пространства могут находиться одновременно поля различных источников и различного происхождения. При этом каждое поле сохраняет свою индивидуальность и ни одна из его характеристик не изменяется под влиянием другого поля. Одним из подтверждений этого является известный всем пример распространения радиоволн, которые являются переменным электромагнитным полем. Радиоволна, распространяющаяся с севера на юг, совсем не влияет на волну, которая распространяется с запада на восток. И слушатель, принимая информацию, которую принесла первая волна, даже не догадывается, что эта волна «встретилась» с другой.
Подобное наблюдается и в том случае, когда есть определенная система заряженных тел и соответствующих им полей.
 |
| Рис. 4.33. Сила, действующая на точечное тело в электрическом поле заряженного тела |
 |
| Рис. 4.34. Силы, действующие на точечное тело в электрическом поле двух заряженных тел |
 |
| Рис. 4.35. Равнодействующая двух сил, действующих на точечное тело |
Пусть в некоторой точке пространства A находится тело, имеющее положительный заряд Q1 (рис. 4.33). Если в произвольную точку B внесем точечное тело с положительным зарядом q0, то на него будет действовать сила F̅1 как результат взаимодействия тела B с полем тела A.
В произвольную точку C внесем тело с зарядом Q2 (рис. 4.34). Его поле будет действовать на тело B с силой F̅2. Никаких изменений в значении силы F̅1не произойдет. Но из механики известно, что, если на тело действует несколько сил, то их можно заменить равнодействующей (рис. 4.35).
В случае нескольких источников электрического поля
F̅ = F̅1 + F̅2 + … + F̅n.
Если левую и правую части уравнения разделить на q0, то получим
F̅ / q0 = F̅1 / q0 + F̅2 / q0 + … + F̅n / q0,
или
E̅ = E̅1 + E̅2 + … + E̅n.
Следовательно, при расчетах взаимодействия заряженного тела с электрическими полями разных источников можно пользоваться понятием напряженности «суммарного» электрического поля. Этот вывод формулируется как принцип суперпозиции полей. Материал с сайта https://worldofschool.ru
Принцип суперпозиции полей. Напряженность электрического поля системы заряженных тел в любой точке равняется векторной сумме напряженностей полей отдельных тел в этой точке.
В математической форме этот принцип записывается так:
E̅ = E̅1 + E̅2 + … + E̅n,
где E̅ — напряженность поля системы заряженных тел; E̅1, E̅2 … —напряженности полей каждого из тел, которые входят в систему.
Напряженность электрического поля тела, имеющего одинаковое количество положительно и отрицательно заряженных частиц, равняется нулю.
Принцип суперпозиции полей не ограничен количеством тел в системе. Именно поэтому напряженность электрического поля незаряженного тела, в состав которого входит огромное количество частиц с положительными и отрицательными зарядами, практически равна нулю.
 На этой странице материал по темам:
На этой странице материал по темам:
Принцип суперпозиции сил формулы
Какое свойство электрического поля описывает напряженность
Принцип суперпозиции электрических полей кратко
Какое выражение является математической записью принципа суперпозиции полей?
Принцип суперпозиции сил формула
 Вопросы по этому материалу:
Вопросы по этому материалу:
Как формулируется принцип суперпозиции полей?
Какое свойство полей положено в основу принципа суперпозиции?
Как понимать выражение «результирующее поле»?
Источник
Закон Кулона, позволяет вычислить
силу взаимодействия между двумя зарядами, но не объясняет, как один заряд
действует на другой. Через какое время, например, один из зарядов
«почувствует», что другой заряд стал приближаться или отдаляться от него? Связаны
ли чем-нибудь между собой заряды? Чтобы ответить на эти вопросы, великие английские
физики М. Фарадей и Дж. Максвелл ввели понятие электрического
поля – материального объекта, существующего вокруг электрических зарядов.
Таким образом, заряд q1 порождает вокруг себя электрическое поле, а другой
заряд q2,
оказавшись в этом поле, испытывает на себе действие заряда q1 согласно закону Кулона . При этом, если положение
зарядаq1
изменились, то изменение его электрического поля будет происходить постепенно,
а не мгновенно, так, что на расстоянии L отq1 изменения поля произойдут через промежуток времени L/c, где с
– скорость света, 3.108 м/с. Запаздывание изменений
электрического поля доказывает то, что взаимодействие между зарядами согласуется
с теорией близкодействия. Эта теория объясняет любое взаимодействие
между телами, даже отдалёнными друг от друга, существованием каких-либо
материальных объектов или процессов между ними. Материальным объектом,
осуществляющим взаимодействие между заряженными телами, является их
электрическое поле.
Чтобы охарактеризовать
данное электрическое поле, достаточно измерить силу, действующую на точечный
заряд в различных областях этого поля. Опыты и закон Кулона показывают,
что сила, действующая на заряд со стороны поля, пропорциональна величине этого
заряда. Поэтому отношение силы F, действующей на заряд в данной точке
поля, к величине этого заряда q, уже не зависит от q и является характеристикой
электрического поля, называемой его напряжённостью, E:
Напряжённость
электрического поля, как следует из (35.1), является вектором, направление
которого совпадает с направлением силы, действующей в данной точке поля на
положительный заряд. Из закона Кулона (34.1) следует, что модуль напряжённости E поля точечного заряда q зависит от расстояния r до него следующим образом:
Векторы
напряжённости в различных точках электрического поля положительного и отрицательного
зарядов показаны на рис. 35а.
Если электрическое поле
образовано несколькими зарядами (q1, q2, q3 и т.д.), то, как показывает опыт, напряжённость E в любой точке этого поля равна сумме
напряжённостей E1, E2, E3 и т.д. электрических полей, создаваемых зарядами q1, q2, q3 и т.д., соответственно:
В этом и
состоит принцип суперпозиции (или наложения) полей, который позволяет
определить напряжённость поля, созданного несколькими зарядами .
Чтобы показать, как
изменяется напряжённость поля в различных его областях, рисуют силовые линии
– непрерывные линии, касательные к которым в каждой точке совпадают с векторами
напряжённости . Силовые линии не могут пересекаться между
собой, т.к. в каждой точке вектор напряжённости поля имеет вполне определённое
направление. Они начинаются и заканчиваются на заряженных телах, вблизи которых
модуль напряжённости и густота силовых линий возрастает. Густота силовых линий
пропорциональна модулю напряжённости электрического поля.
Различные тела можно наэлектризовать по-разному: передать им
положительный или отрицательный заряд, сделать его большим или малым.
После этого тела будут по-разному действовать на другие тела:
отталкивать или притягивать их, делать это сильнее или слабее. Но как
одно тело «узнаёт» заряд другого (например, чтобы «знать»: притягивать
его или отталкивать)? Для ответа на этот вопрос рассмотрим понятие
«электрическое поле».
Наэлектризуем одноимённо металлический шар на пластмассовой
подставке и лёгкий пробковый или пенопластовый шарик на нити (назовём
его пробным шариком). Будем переносить его в различные точки
пространства вокруг большого шара (см. рисунок). Мы заметим, что в каждой точке пространства вокруг наэлектризованного тела обнаруживается сила, действующая на пробный шарик.
О том, что существует сила, мы судим по отклонению нити шарика от
вертикали. По мере удаления от заряженного шара пробный шарик
отклоняется всё слабее, следовательно, действующая на него сила
становится всё меньше (сравните положения а, б, в).
Для следующего опыта используем магнит и стальной шарик, который
положим на горизонтальную поверхность стола. Приблизим магнит к шарику
сверху, и он незамедлительно покатится по столу вслед за магнитом.
Следовательно, в каждой точке пространства вокруг намагниченного тела есть сила, действующая на стальной шарик.
Итак, в каждой точке пространства вокруг наэлектризованных или намагниченных тел существует так называемое силовое поле, способное воздействовать на другие тела.
Заметим, что действие силы тяжести также обнаруживается во всех точках
пространства вокруг Земли. Поэтому по аналогии говорят, что в
пространстве вокруг планет также существует силовое поле; его называют гравитационным полем.
Обобщаем: гравитационное, магнитное и электрическое поле являются разновидностями силовых полей. На примере электрического поля рассмотрим один из методов изучения полей – метод силовых линий.
Проведём опыт. Возьмём два металлических шара на пластмассовых
подставках, а также иглу, тоже укреплённую на подставке. Расположим шары
на расстоянии 40–50 см друг от друга, а между ними – подставку с иглой.
Уравновесим на ней сухую деревянную щепку.
Если зарядить шары разноимённо, мы увидим, что щепка развернётся
так, чтобы находиться на прямой, соединяющей шары (см. верхнюю часть
рисунка).
Будем помещать щепку в различные места вокруг шаров (см. нижнюю
часть рисунка, слева). Заметим, что щепка занимает такие положения,
которые «ложатся» на мысленно проведённые дугообразные линии,
соединяющие шары; их называют силовыми линиями электрического поля.
Если тела наэлектризованы одноимённо или если мы имеем только одно
тело, силовые линии также можно изучать с помощью щепки на игле. Однако
проще – при помощи мелко стриженных волос. Опишем этот способ. Над
заряженными телами необходимо поместить стекло и посыпать его стриженным
волосом. Под действием поля каждый волосок поворачивается определённым
образом, и образуется «картина» (см. рисунки). Слева и справа показано
расположение волос вокруг одноимённо заряженных шаров, а в центре –
разноимённо заряженных шаров, как в опыте со щепкой.
Изображение силовых линий поля – метод для описания электрических полей. Силовые линии изображают более «густыми» там, где обнаруживается большая сила воздействия поля на тело или тела. Но не следует думать, что силовые линии действительно существуют внутри поля; это физическая модель. Она описывает силу и направление действия поля на помещаемые в него тела (в последнем примере – электрического поля).
В заключение осталось лишь добавить очевидное: электрическое поле
всегда «привязано» к заряду, его создавшему, и при перемещении заряда в
другую точку пространства электрическое поле практически мгновенно перемещается вслед за зарядом, действуя на другие тела.
Источник
