Какое свойство электрического поля описывает напряженность
Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и равная отношению силы , действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда [1]:
Напряжённость электрического поля иногда называют силовой характеристикой электрического поля, так как всё отличие от вектора силы, действующей на заряженную частицу, состоит в постоянном[2] множителе.
В каждой точке в данный момент времени существует своё значение вектора (вообще говоря — разное[3]
в разных точках пространства), таким образом, — это векторное поле. Формально это отражается в записи
представляющей напряжённость электрического поля как функцию пространственных координат (и времени, так как может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле[4], и законы, которым оно подчиняется, есть предмет электродинамики.
Напряжённость электрического поля в Международной системе единиц (СИ) измеряется в вольтах на метр [В/м] или в ньютонах на кулон [Н/Кл].
Напряжённость электрического поля в классической электродинамике[править | править код]
Напряжённость электрического поля — одна из основных фундаментальных величин классической электродинамики. В этой области физики сопоставимыми с ней по значимости являются только вектор магнитной индукции (совместно с вектором напряжённости электрического поля образующий тензор электромагнитного поля) и электрический заряд. С некоторой точки зрения столь же важными представляются потенциалы электромагнитного поля (образующие вместе единый электромагнитный потенциал).
Остальные понятия и величины классической электродинамики, такие как электрический ток, плотность тока, плотность заряда, вектор поляризации, а также вспомогательные поле электрической индукции и напряженность магнитного поля — хотя безусловно важны и содержательны, по сути оказываются вторичными или производными.
Ниже выделены основные контексты классической электродинамики в отношении напряжённости электрического поля.
Сила, с которой электромагнитное поле действует на заряженные частицы[править | править код]
Полная сила, с которой электромагнитное поле (включающее, вообще говоря, электрическую и магнитную составляющие) действует на заряженную частицу, выражается формулой силы Лоренца:
где — электрический заряд частицы, — её скорость,
— вектор магнитной индукции (основная характеристика магнитного поля); косым крестом обозначено векторное произведение. Формула приведена в единицах СИ.
Эта формула является более общей по сравнению с формулой, данной в определении напряжённости электрического поля, так как включает в себя также действие на заряженную частицу (если та движется) со стороны магнитного поля.
Частица предполагается точечной. Однако эта формула позволяет рассчитать и силы, действующие со стороны электромагнитного поля на тела любой формы с любым распределением зарядов и токов — если воспользоваться обычным для физики приёмом разбиения сложного тела на маленькие (математически — бесконечно малые) части, каждая из которых может считаться точечной и таким образом входящей в область применимости формулы Лоренца. Разумеется, для того, чтобы эта формула была применена (даже в простых случаях, таких, как расчёт силы взаимодействия двух точечных зарядов), необходимо уметь рассчитывать и .
Остальные формулы, применяемые для расчёта электромагнитных сил (например, формулу для силы Ампера) можно считать следствиями[5] фундаментальной формулы силы Лоренца или частными случаями её применения.
Уравнения Максвелла[править | править код]
Достаточным вместе с формулой силы Лоренца теоретическим фундаментом классической электродинамики являются уравнения электромагнитного поля, называемые уравнениями Максвелла. Их стандартная традиционная форма представляет собой четыре уравнения, в три из которых входит вектор напряжённости электрического поля:
Здесь — плотность заряда, — плотность тока, — электрическая постоянная, — магнитная постоянная, — скорость света (уравнения записаны в системе СИ). В приведённом виде уравнения Максвелла являются «уравнениями для вакуума» (их более общий вариант, применимый и для описания поведения электромагнитного поля в среде, а также иные формы записи уравнений — см. в статье Уравнения Максвелла).
Этих четырёх уравнений вместе с пятым — уравнением силы Лоренца — в принципе достаточно, чтобы полностью описать классическую (не квантовую) электродинамику, то есть они представляют её полные законы. Для решения реальных задач с их помощью необходимы ещё уравнения движения «материальных частиц» (в классической механике это законы Ньютона), а также дополнительная информация о конкретных свойствах рассматриваемых физических тел и сред (их упругости, электропроводности, поляризуемости и др.) и о других силах, участвующих в задаче (например, о гравитации), однако вся эта информация уже не входит в рамки электродинамики как таковой, хотя и оказывается зачастую необходимой для построения замкнутой системы уравнений, позволяющих решить ту или иную конкретную задачу в целом.
«Материальные уравнения»[править | править код]
Дополнительными формулами (обычно не точными, а приближёнными или иногда даже эмпирическими), которые используются в классической электродинамике при решении практических задач и носят название «материальных уравнений», являются
- закон Ома;
- закон поляризации;
- в разных случаях многие другие формулы и соотношения.
Связь с потенциалами[править | править код]
Связь напряжённости электрического поля с потенциалами в общем случае такова:
где — скалярный и векторный потенциалы,
В частном случае стационарных (не меняющихся со временем) полей первое уравнение упрощается до
Это выражение связывает электростатическое поле с электростатическим потенциалом.
Электростатика[править | править код]
Теоретически и практически важным случаем является ситуация, когда заряженные тела неподвижны (например, исследуется состояние равновесия) или скорость их движения достаточно мала, чтобы можно было приближённо воспользоваться способами расчета, справедливыми для неподвижных тел. Этим случаем занимается раздел электродинамики, называемый электростатикой.
Как указано выше, напряжённость электрического поля в этом случае выражается через скалярный потенциал как
или
то есть электростатическое поле оказывается потенциальным полем.
( в этом случае — случае электростатики — принято называть электростатическим потенциалом).
Правомерно и обратное соотношение:
Уравнения Максвелла при этом также сильно упрощаются (уравнения с магнитным полем можно вообще исключить, а в уравнение с дивергенцией можно подставить ) и сводятся к уравнению Пуассона:
а в областях, свободных от заряженных частиц, — к уравнению Лапласа:
Учитывая линейность этих уравнений, а следовательно, применимость к ним принципа суперпозиции, достаточно найти поле одного точечного единичного заряда, чтобы потом найти потенциал или напряжённость поля, создаваемого любым распределением зарядов (суммируя решения для точечных зарядов).
Теорема Гаусса[править | править код]
В электростатике широко используется теорема Гаусса, содержание которой сводится к интегральной форме единственного нетривиального для электростатики уравнения Максвелла:
где интегрирование производится по любой замкнутой поверхности (вычисляя поток
через эту поверхность), — полный (суммарный) заряд внутри этой поверхности.
Эта теорема даёт удобный способ расчета напряжённости электрического поля в случае, когда источники поля имеют высокую симметрию: сферическую, цилиндрическую или зеркальную + трансляционную. В частности, таким способом легко находится поле точечного заряда, сферы, цилиндра, плоскости.
Напряжённость электрического поля точечного заряда[править | править код]
В единицах СИ[править | править код]
Для точечного заряда в электростатике верен закон Кулона
или
Исторически закон Кулона был открыт первым, хотя с теоретической точки зрения уравнения Максвелла более фундаментальны. С этой точки зрения он является их следствием. Получить этот результат проще всего, исходя из теоремы Гаусса, учитывая сферическую симметрию задачи: выбрать поверхность в виде сферы с центром в точечном заряде, учесть, что направление будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса : , имеем:
откуда сразу получаем ответ для .
Ответ для получается интегрированием :
Для системы СГС[править | править код]
Формулы и их вывод аналогичны, отличие от СИ лишь в константах.
Напряжённость электрического поля произвольного распределения зарядов[править | править код]
По принципу суперпозиции для напряжённости поля совокупности дискретных источников имеем:
где каждое
Подставив, получаем:
Для непрерывного распределения аналогично:
где — область пространства, где расположены заряды (ненулевая плотность заряда), или всё пространство,
— радиус-вектор точки, для которой считаем ,
— радиус-вектор источника, пробегающий все точки области при интегрировании, — элемент объёма. Можно подставить вместо ;
вместо ;
вместо
Системы единиц[править | править код]
В системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в ньютонах на кулон или в вольтах на метр (русское обозначение: В/м; международное: V/m).
Литература[править | править код]
- Сивухин Д. В. Общий курс физики. — Изд. 4-е, стереотипное. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — 656 с. — ISBN 5-9221-0227-3; ISBN 5-89155-086-5..
Примечания[править | править код]
- ↑ Напряжённость электрического поля // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 246. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Для любой частицы её электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или если к ней что-то заряженное присоединится.
- ↑ Иногда его значения могут оказываться и одинаковыми в разных точках пространства; если одинаков всюду в пространстве (или в какой-то области), говорят об однородном электрическом поле — это частный, наиболее простой, случай электрического поля; в реальности электрическое поле может быть однородным лишь приближённо, то есть различия в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.
- ↑ Электромагнитное поле может быть выражено и по-другому, например через электромагнитный потенциал или в несколько иной математической записи (в которой вектор напряжённости электрического поля вместе с вектором магнитной индукции входит в тензор электромагнитного поля), однако все эти способы записи тесно связаны между собой, таким образом, утверждение о том, что поле — одна из основных составляющих электромагнитного поля, не утрачивает смысла.
- ↑ Хотя исторически многие из них были открыты раньше.
См. также[править | править код]
- Электрическая индукция
- Уравнения Максвелла
- Закон Кулона
Источник
Электростатическое поле и его характеристики
Электрический заряд, помещенный в некоторую точку пространства, изменяет свойства данного пространства. То есть заряд порождает вокруг себя электрическое поле. Электростатическое поле – особый вид материи.
Электростатическое поле существующий вокруг неподвижный заряженных тел, действует на заряд с некоторой силой, вблизи заряда – сильнее.
Электростатическое поле не изменяется во времени.
Силовой характеристикой электрического поля является напряженность
Напряженностью электрического поля в данной точке называется векторная физическая величина, численно равная силе, действующей на единичный положительный заряд, помещенный в данную точку поля.
За единицу измерения напряженности электрического поля в СИ принимают
Если на пробный заряд, действуют силы со стороны нескольких зарядов, то эти силы по принципу суперпозиции сил независимы, и результирующая этих сил равна векторной сумме сил. Принцип суперпозиции (наложения) электрических полей: Напряженность электрического поля системы зарядов в данной точке пространства равна векторной сумме напряженностей электрических полей, создаваемых в данной точке пространства, каждым зарядом системы в отдельности:
или
Электрическое поле удобно представлять графически с помощью силовых линий.

Силовыми линиями (линиями напряженности электрического поля) называют линии, касательные к которым в каждой точке поля совпадают с направлением вектора напряженности в данной точке.
Силовые линии начинаются на положительном заряде и заканчиваются на
отрицательном (Силовые линии электростатических полей точечных зарядов.).

Густота линий напряженности характеризует напряженность поля (чем
плотнее располагаются линии, тем поле сильнее).
Электростатическое поле точечного заряда неоднородно (ближе к заряду поле сильнее).
Силовые линии электростатических полей бесконечных равномерно заряженных плоскостей.
Электростатическое поле бесконечных равномерно заряженных плоскостей однородно. Электрическое поле, напряженность во всех точках которого одинакова, называется однородным.
Силовые линии электростатических полей двух точечных зарядов.
Потенциал – энергетическая характеристика электрического поля.
Потенциал – скалярная физическая величина, равная отношению потенциальной энергии, которой облает электрический заряд в данной точке электрического поля, к величине этого заряда.
Потенциал показывает какой потенциальной энергией будет обладать единичный положительный заряд, помещенный в данную точку электрического поля. φ = W / q
где φ – потенциал в данной точке поля, W- потенциальная энергия заряда в данной точке поля.
За единицу измерения потенциала в системе СИ принимают [φ] = В (1В = 1Дж/Кл )
За единицу потенциала принимают потенциал в такой точке, для перемещения в которую из бесконечности электрического заряда 1 Кл, требуется совершить работу, равную 1 Дж.
Рассматривая электрическое поле, созданное системой зарядов, следует для определения потенциала поля использовать принцип суперпозиции:
Потенциал электрического поля системы зарядов в данной точке пространства равен алгебраической сумме потенциалов электрических полей, создаваемых в данной точке пространства, каждым зарядом системы в отдельности:
Вектор напряженности в данной точке поля всегда направлен в область уменьшения потенциала.
Воображаемая поверхность, во всех точках которой потенциал принимает одинаковые значения, называется эквипотенциальной поверхностью. При перемещении электрического заряда от точки к точке вдоль эквипотенциальной поверхности энергия его не меняется. Эквипотенциальных поверхностей для заданного электростатического поля может быть построено бесконечное множество.
Вектор напряженности в каждой точке поля всегда перпендикулярен к эквипотенциальной поверхности, проведенной через данную точку поля.
Источник
Электрические заряды не воздействуют непосредственно друг на друга. Согласно современным представлениям, заряженные тела взаимодействуют посредством силового поля, которое создают вокруг себя.
Это силовое поле воздействует на заряженные тела с некоторой силой. Исследовать электрическое поле, которое окружает тело, несущее заряд, можно с помощью пробного заряда, величина которого незначительна. Особенностью электрического поля точечного заряда является тот факт, что оно не производит заметного перераспределения исследуемых зарядов.
Понятие напряженности электрического поля
Определение 1
Напряженность электрического поля – это силовая характеристика, которая используется для количественного определения электрического поля.
Второе значение термина – физическая величина, равная отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда.
Напряженность электрического поля можно задать формулой:
E→=F→q.
Напряжение электрического поля является векторной величиной. Направление вектора E→ совпадает с направлением силы, которая воздействует на положительный пробный заряд в пространстве.
Напряженность электрического поля
Какое поле называют электростатическим?
Определение 2
Электростатическое поле – это электрическое поле, которое окружает неподвижные и не меняющиеся со временем заряды.
Очень часто в контексте темы электростатическое поле будет именоваться электрическим для краткости.
Электрическое поле может быть создано сразу несколькими заряженными телами. Такое поле также можно исследовать с помощью пробного заряда. В этом случае мы будем оценивать результирующую силу, которая будет равна геометрической сумме сил каждого из заряженных тем в отдельности.
Определение 3
Напряженность электрического поля, которая создается в определенной точке пространства системой зарядов, будет равна векторной сумме напряженностей электрических полей:
E→=E1→+E2→+…
Электрическое поле подчиняется принципу суперпозиции.
Определение 4
Согласно формуле, напряженность электростатического поля, которое создается точечным зарядом Q на расстоянии r от него, в соответствии с законом Кулона, будет равна по модулю:
E=14πε0·Qr2.
Это поле называется кулоновским.
В кулоновском поле направление вектора E⇀ зависит от знака заряда Q: если Q>0, то вектор E⇀ направлен по радиусу от заряда, если Q<0, то вектор E⇀ направлен к заряду.
Обратимся к иллюстрации. На рисунке для большей наглядности мы используем силовые линии электрического поля. Они проходят таким образом, чтобы направление вектора E⇀ в каждой из точек пространства совпадало с направлением касательной к силовой линии. Густота силовых линий соответствует модулю вектора напряженности поля.
Рисунок 1.2.1. Силовые линии электрического поля.
Мы можем использовать как положительные, так и отрицательные точечные заряды. Оба эти случая мы изобразили на рисунке. Электростатическое поле, которое создается системой зарядов, мы можем представить как суперпозицию кулоновских полей точечных зарядов. В связи с этим мы можем рассматривать поля точечных зарядов как элементарные структурные единицы любого электрического поля.
Рисунок 1.2.2. Силовые линии кулоновских полей.
Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор r→от заряда Q к точке наблюдения. Тогда при Q>0 вектор E→ параллелен r→, а при Q<0 вектор E→ антипараллелен r→.
Следовательно можно записать:
E→=14πε0·Qr3r→,
где r – модуль радиус-вектора r→.
По заданному распределению зарядов можно определить электрическое поле E→. Такие задачи часто встречаются в таком разделе физики как электростатика. Рассмотрим пример такой задачи.
Пример 1
Предположим, что нам нужно найти электрическое поле длинной однородно заряженной нити на расстоянии R от нее. Для большей наглядности мы привели схему на рисунке ниже.
Рисунок 1.2.3. Электрическое поле заряженной нити.
Поле в точке наблюдения P может быть представлено в виде суперпозиции кулоновских полей, создаваемых малыми элементами Δx нити, с зарядом τΔx, где τ – заряд нити на единицу длины. Задача сводится к суммированию (интегрированию) элементарных полей ∆E→. Результирующее поле оказывается равным
E=τ2πε0R.
Вектор E→ везде направлен по радиусу R→. Это следует из симметрии задачи.
Даже в таком простом примере вычисления могут быть достаточно громоздкими. Упростить математические расчеты позволяет теорема Гаусса, которая выражает фундаментальное свойство электрического поля.
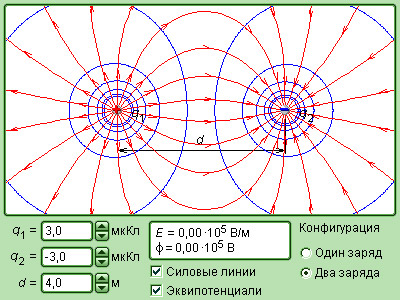
Рисунок 1.2.4. Модель электрического поля точечных зарядов.
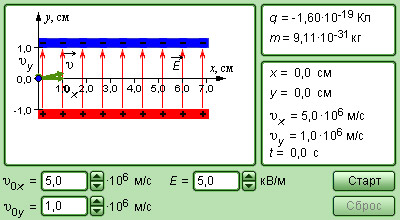
Рисунок 1.2.5. Модель движения заряда в электрическом поле.
Понятие о диполях
Определение 5
Электрический диполь – это система из двух одинаковых по модулю зарядов, которые отличаются знаками и расположены на некотором расстоянии друг от друга.
Эта система может послужить нам хорошим примером применения принципа суперпозиции полей, а также электрической моделью многих молекул.
Рисунок 1.2.6. Силовые линии поля электрического диполя E→=E1→+E2→.
Дипольный момент p→ является одной из наиболее важных характеристик электрического диполя:
p→=l→q,
где l→ – вектор, направленный от отрицательного заряда к положительному, модуль l→=l.
Электрическим дипольным моментом обладает, например, нейтральная молекула воды (H2O), так как центры двух атомов водорода располагаются не на одной прямой с центром атома кислорода, а под углом 105°. Дипольный момент молекулы воды p=6,2·10–30 Кл · м.
Рисунок 1.2.7. Дипольный момент молекулы воды.
Источник
