Какое свойство имеют параллельные прямые
В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.
Параллельные прямые: основные сведения
Определение 1
Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.
Определение 2
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.
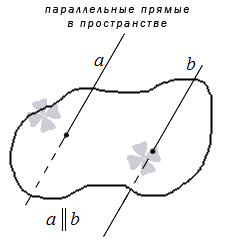
Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.
Чтобы обозначить параллельность прямых, общепринято использовать символ ∥. Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b. Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b, или прямая b параллельна прямой а.
Сформулируем утверждение, играющее важную роль в изучаемой теме.
Аксиома
Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.
В случае, когда речь идет о пространстве, верна теорема:
Теорема 1
Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.
Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10-11 классов).
Параллельность прямых: признаки и условия параллельности
Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.
В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.
Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.
Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.
Определение 3
Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.
Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Теорема 2
Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.
Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

Доказательство указанных условий присутствует в программе геометрии за 7-9 классы.
В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.
Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.
Теорема 3
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.
Теорема 4
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.
Доказательство признака изучается в программе геометрии 10 класса.
Дадим иллюстрацию указанных теорем:
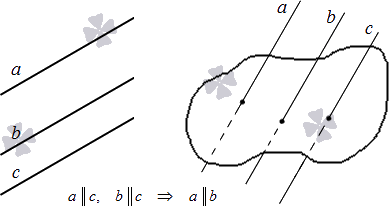
Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.
Теорема 5
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.
Сформулируем аналогичное для трехмерного пространства.
Теорема 6
В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.
Проиллюстрируем:
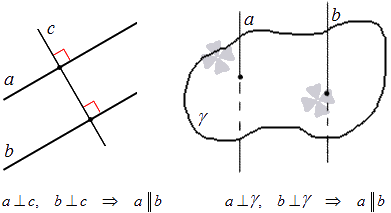
Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.
Параллельность прямых в прямоугольной системе координат
В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.
Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.
Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.
Теорема 7
Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.
Становится очевидно, что условие параллельности прямых на плоскости базируется на условии коллинеарности векторов или условию перпендикулярности двух векторов. Т.е., если a→=(ax, ay) и b→=(bx, by) являются направляющими векторами прямых a и b;
и nb→=(nbx, nby) являются нормальными векторами прямых a и b, то указанное выше необходимое и достаточное условие запишем так: a→=t·b→⇔ax=t·bxay=t·by или na→=t·nb→⇔nax=t·nbxnay=t·nby или a→, nb→=0⇔ax·nbx+ay·nby=0, где t – некоторое действительное число. Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.
- Прямая a в прямоугольной системе координат определяется общим уравнением прямой: A1x+B1y+C1=0; прямая b – A2x+B2y+C2=0. Тогда нормальные векторы заданных прямых будут иметь координаты (А1, В1) и (А2, В2) соответственно. Условие параллельности запишем так:
A1=t·A2B1=t·B2
- Прямая a описывается уравнением прямой с угловым коэффициентом вида y=k1x+b1. Прямая b – y=k2x+b2. Тогда нормальные векторы заданных прямых будут иметь координаты (k1, -1) и (k2, -1) соответственно, а условие параллельности запишем так:
k1=t·k2-1=t·(-1)⇔k1=t·k2t=1⇔k1=k2
Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.
- Прямые a и b в прямоугольной системе координат заданы каноническими уравнениями прямой на плоскости: x-x1ax=y-y1ay и x-x2bx=y-y2by или параметрическими уравнениями прямой на плоскости: x=x1+λ·axy=y1+λ·ay и x=x2+λ·bxy=y2+λ·by.
Тогда направляющие векторы заданных прямых будут: ax, ay и bx, by соответственно, а условие параллельности запишем так:
ax=t·bxay=t·by
Разберем примеры.
Пример 1
Заданы две прямые: 2x-3y+1=0 и x12+y5=1. Необходимо определить, параллельны ли они.
Решение
Запишем уравнение прямой в отрезках в виде общего уравнения:
x12+y5=1⇔2x+15y-1=0
Мы видим, что na→=(2, -3) – нормальный вектор прямой 2x-3y+1=0, а nb→=2, 15- нормальный вектор прямой x12+y5=1.
Полученные векторы не являются коллинеарными, т.к. не существует такого значения t, при котором будет верно равенство:
2=t·2-3=t·15⇔t=1-3=t·15⇔t=1-3=15
Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.
Ответ: заданные прямые не параллельны.
Пример 2
Заданы прямые y=2x+1и x1=y-42. Параллельны ли они?
Решение
Преобразуем каноническое уравнение прямой x1=y-42 к уравнению прямой с угловым коэффициентом:
x1=y-42⇔1·(y-4)=2x⇔y=2x+4
Мы видим, что уравнения прямых y = 2x + 1 и y = 2x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.
Попробуем решить задачу иначе. Сначала проверим, совпадают ли заданные прямые. Используем любую точку прямой y = 2x + 1, например, (0, 1), координаты этой точки не отвечают уравнению прямой x1=y-42, а значит прямые не совпадают.
Следующим шагом определим выполнение условия параллельности заданных прямых.
Нормальный вектор прямой y = 2x + 1 это вектор na→=(2, -1), а направляющий вектором второй заданной прямой является b→=(1, 2). Скалярное произведение этих векторов равно нулю:
na→, b→=2·1+(-1)·2=0
Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.
Ответ: данные прямые параллельны.
Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.
Теорема 8
Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.
Т.е. при заданных уравнениях прямых в трехмерном пространстве ответ на вопрос: параллельны они или нет, находится при помощи определения координат направляющих векторов заданных прямых, а также проверки условия их коллинеарности. Иначе говоря, если a→=(ax, ay, az) и b→=(bx, by, bz)являются направляющими векторами прямых a и b соответственно, то для того, чтобы они были параллельны, необходимо существование такого действительного числа t, чтобы выполнялось равенство:
a→=t·b→⇔ax=t·bxay=t·byaz=t·bz
Пример 3
Заданы прямые x1=y-20=z+1-3 и x=2+2λy=1z=-3-6λ. Необходимо доказать параллельность этих прямых.
Решение
Условиями задачи заданы канонические уравнения одной прямой в пространстве и параметрические уравнения другой прямой в пространстве. Направляющие векторы a→ и b→ заданных прямых имеют координаты: (1, 0, -3) и (2, 0, -6).
Так как:
1=t·20=t·0-3=t·-6⇔t=12, то a→=12·b→.
Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.
Ответ: параллельность заданных прямых доказана.
Источник
Что такое параллельные прямые
Определение
Параллельные прямые — в планиметрии прямые, которые не пересекаются, сколько бы их ни продолжали в обе стороны. В стереометрии две прямые называются параллельными, если лежат в одной плоскости и не пересекаются.
Основные признаки:
- В случае, если две прямые параллельны третьей, они являются параллельными между собой. Так, если а || c и также b || c, то и a || b.
- Если они перпендикулярны по отношению к третьей, то они не пересекаются: т.е., если а ⊥ с и b ⊥ c, то a || b.


Свойства параллельных прямых с доказательством
Определение
Свойства параллельных прямых — это утверждения, являющиеся обратными по отношению к признакам, упомянутым ранее.
Они обладают следующими свойствами:
- Через любую точку, которая, что немаловажно, не лежит на прямой, можно провести параллель, притом лишь одну. Данное утверждение является Евклидовой аксиомой.
- Если прямая, лежащая на плоскости, перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой: если a || b и c ⊥ a, то c ⊥ b.

Дано: a || b и c ⊥ a
Доказать: c ⊥ b
Доказательство:
- с пересекает а, следовательно, с пересекает также прямую, параллельную а, т.е. b.
- Исходя из этого, можно утверждать, что с — это секущая по отношению к а и b.
- При секущей с ∠1 и ∠2 являются накрест лежащими.
- Из свойств углов при параллельных прямых, пересеченных секущей, нам известно о равенстве накрест лежащих углов: следовательно, ∠1 = ∠2.
- Как следствие, ∠2 = 90 градусов, что означает, что c ⊥ b. Что и требовалось доказать.
Признаки при пересечении секущей
Определение
Секущей называется прямая, пересекающая:
- кривую в двух точках;
- или две прямые, которые лежат в этой же плоскости, в двух разных точках.
Рассмотрим признаки, которые характерны для параллельных прямых при пересечении их секущей.
Если соответственные углы равны, то прямые не пересекаются. Если ∠2 = ∠4, следовательно, a || b.

Если сумма внутренних односторонних углов равняется 180 градусам, то прямые являются параллельными. Если ∠1 + ∠2 = 180°, следовательно, a || b.

Если внутренние накрест лежащие углы равны, то прямые также являются параллельными. Если ∠1 = ∠3, следовательно, a || b.

Свойства углов при параллельных прямых и секущей
Кроме того, следует охарактеризовать основные свойства углов, образованных при пересечении секущей прямой. Данные свойства являются обратными рассмотренным выше признакам.
При пересечении двух параллельных прямых третьей, сумма внутренних односторонних углов, образованных ими, равняется 180 градусам: если a || b, то ∠1 + ∠2 = 180°.

В случае, когда две параллельные прямые пересечены третьей, соответственные углы, образованные ими, равны: если a || b, то ∠2 = ∠4.

Если две параллельные прямые пересекаются третьей, накрест лежащие углы, образованные ими, равны: если a || b, то ∠1 = ∠3.

Источник
Параллельные прямые – подарок судьбы в решении многих задач.
Они дают тебе множество равных углов! И на них основывается много признаков фигур.
Что, безусловно, будет очень полезно.
Читай эту статью – будешь знать о них все!
И получишь заслуженные баллы на ЕГЭ.
Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их не продолжали.
Вот, как рельсы
Принято обозначение:
( displaystyle a//b) – читается как ( displaystyle a) параллельна ( displaystyle b).
Самым важным фактом, который нужно принять без доказательства (не только тебе, но и любому математику) для того, чтобы вся геометрия не развалилась и не превратилась в какую-то неузнаваемую теорию, является так называемая «аксиома параллельных прямых».
Часто ее еще называют «пятый постулат Евклида». Формулируем:
Через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной.
Смотри: через любую точку ( displaystyle A) проходит только одна прямая ( displaystyle b), которая параллельна ( displaystyle a), все остальные будут пересекать прямую ( displaystyle a).
Казалось бы: чего проще – ну, одна так одна…
Но ты себе просто не представляешь, сколько споров вели математики на протяжении прямо-таки тысячелетий, прежде чем осознали истинную роль этой аксиомы о параллельных прямых.
В конце концов, уже в 19-м веке, после открытий Лобачевского, Гаусса и других ученых стало ясно, что можно построить и другие виды геометрии, в которых не выполняется аксиома параллельных прямых, в которых ее можно выбросить, но эти геометрии уже оказываются не геометриями плоскости, а геометриями на каких-то хитрых поверхностях.
А наша привычная плоскость оттого и называется евклидовой, что при построении геометрии на ней, при решении всех задачек и доказательстве теорем мы считаем этот многострадальный пятый постулат Евклида выполнимым.
Ну вот, а теперь возникает два вопроса:
1
Если где-то в задаче даны или оказались параллельными две какие-то прямые, то что? Как это использовать?
2
А как вообще узнать, что какие-то прямые параллельны?
Ответ на первый вопрос называется «свойства параллельных прямых», а ответ на второй вопрос называется «признаки параллельных прямых».
Но прежде нам понадобится много названий, которые нужно запомнить, как таблицу умножения.
Итак, ситуация: две прямые пересечены третьей (она называется секущей)
Получается куча углов. Целых ( displaystyle 8) штук.
Приняты такие названия этих углов:
( displaystyle angle 4) и ( displaystyle angle 6) называются внутренними накрест лежащими углами
( displaystyle angle 3) и ( displaystyle angle5) – тоже внутренние накрест лежащие углы.
Название говорит само за себя: ( displaystyle angle 4) и ( displaystyle angle 6), так же, как и ( displaystyle angle 3) и ( displaystyle angle5) лежат «накрест» – по разные стороны от секущей и «внутри», между прямыми ( displaystyle a) и ( displaystyle b).
( displaystyle angle 5) и ( displaystyle angle 4) (а еще ( displaystyle angle 6) и ( displaystyle angle 3)) называются внутренними односторонними углами.
Они лежат с одной стороны от секущей и «внутри» между прямыми ( displaystyle a) и ( displaystyle b).
( displaystyle angle 1) и ( displaystyle angle 8) (а еще ( displaystyle angle 2) и ( displaystyle angle 7)) называются внешними односторонними углами (ты уже догадался, почему?)
И последнее название: соответственные углы.
Это пары углов:
- ( displaystyle angle 1) и ( displaystyle angle 5)
- ( displaystyle angle 4) и ( displaystyle angle 8)
- ( displaystyle angle 2) и ( displaystyle angle 6)
- ( displaystyle angle 3) и ( displaystyle angle 7)
Обрати внимание, ( displaystyle angle 1) и ( displaystyle angle 5) лежат в одинаковых «соответственных» местах около точек ( displaystyle A) и ( displaystyle B). То же можно сказать и об остальных перечисленных парах – посмотри на рисунок.
Напоминаем (а то отвлеклись на названия), что пытаемся ответить на вопрос: если ( displaystyle a//b), то что?
И вот что:
Если две параллельные прямые пересечены третьей (секущей) прямой, то:
- Внутренние накрест лежащие углы равны
- Соответственные углы равны
- Сумма любых двух внутренних односторонних равна ( displaystyle 180{}^circ )
Запомни – все задачи с участием слова «параллельность» решаются с помощью этой теоремы о свойствах параллельных прямых.
А теперь, наоборот, признаки параллельных прямых.
То есть, как бы узнать, что прямые параллельны?
Если две прямые (( displaystyle a) и ( displaystyle b)) пересечены третьей и оказалось, что
- Какие-нибудь два накрест лежащих угла равны
ИЛИ - Какие нибудь два соответственных угла равны
ИЛИ - Сумма хоть каких-то двух внутренних односторонних равна ( displaystyle 180{}^circ )
ИЛИ - Сумма хоть каких – то двух внешних односторонних равна ( displaystyle 180{}^circ ),
то прямые ( displaystyle a) и ( displaystyle b) – параллельны
Заметь, что для того, чтобы установить параллельность прямых, достаточно выяснить, скажем, равенство всего двух углов (или накрест лежащих, или соответственных), а уже все остальное окажется , так сказать, бонусом.
Смотри-ка, вот схема:
Параллельные прямые – это прямые, которые лежат в одной плоскости и не пересекаются, сколько бы их не продолжали: ( displaystyle aparallel b).
Секущая – прямая, пересекающая две параллельные прямые: ( displaystyle c).
Аксиома параллельных прямых: через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной.
- ( displaystyle angle 4) и ( displaystyle angle 6), ( displaystyle angle 3) и ( displaystyle angle5)
– внутренние накрест лежащие углы; - ( displaystyle angle 5) и ( displaystyle angle 4), ( displaystyle angle 6) и ( displaystyle angle 3) – внутренние односторонние углы;
- ( displaystyle angle 1) и ( displaystyle angle 8), ( displaystyle angle 2) и ( displaystyle angle 7) – внешние односторонние углы;
- ( displaystyle angle 1) и ( displaystyle angle 5), ( displaystyle angle 4) и ( displaystyle angle 8), ( displaystyle angle 2) и ( displaystyle angle 6), ( displaystyle angle 3) и ( displaystyle angle 7) – соответственные углы.
Свойства параллельных прямых
Если две параллельные прямые пересечены третьей (секущей) прямой, то:
- внутренние накрест лежащие углы равны: ( displaystyle angle 3=angle 5), ( displaystyle angle 4=angle 6);
- соответственные углы равны: ( displaystyle angle 1=angle 5), ( displaystyle angle 4=angle 8), ( displaystyle angle 2=angle 6), ( displaystyle angle 3=angle 7);
- сумма любых двух внутренних односторонних углов равна ( displaystyle 180{}^circ ): ( displaystyle angle 3+angle 6=180{}^circ ), ( displaystyle angle 4+angle 5=180{}^circ );
- сумма любых двух внешних односторонних углов равна ( displaystyle 180{}^circ ): ( displaystyle angle 1+angle 8=180{}^circ ), ( displaystyle angle 2+angle 7=180{}^circ ).
Признаки параллельных прямых
P.S. Последний бесценный совет ????
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
- проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
- подтянуть слабые места с помощью видеоуроков, вебинаров;
- понять тему с помощью статей учебника YouClever;
- набить руку, решая задачи и получая проверку и решения;
- сдать пробный ЕГЭ и получить сразу оценку и разбор ошибок.
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Твой час настал!
Параллельные прямые – очень важная тема. Ты будешь встречать их чуть ли не в каждой задаче по геометрии! И они во многом тебе помогут.
А теперь ты знаешь о них все! И справишься с любой задачей!
Как тебе статья? Понравилась? ????
Напиши в комментариях ниже! Все ли было понятно?
Ты можешь задать нам любой вопрос. Мы ответим!
Мы читаем все.
Удачи!
Источник
