Какое свойство характеризует емкость

Одним из важных параметров, учитываемых в электрических цепях, является электрическая емкость – способность проводников накапливать заряды. Понятие емкости применяется как для уединенного проводника, так и для системы, состоящей из двух и более проводников. В частности, емкостью обладают конденсаторы, состоящие из двух металлических пластин, разделенных диэлектриком или электролитом.
Для накопления зарядов широко применяютсяаккумуляторы, используемые в качестве источников постоянного тока для питания различных устройств. Количественной характеристикой, определяющей время работы аккумулятора, является его электроемкость.
Определение
Если диэлектрик, например, эбонитовую палочку, наэлектризовать трением то электрические заряды сконцентрируются в местах соприкосновения с электризующим материалом. При этом, другой конец палочки можно насытить зарядами противоположно знака и такая наэлектризованность будет сохраняться.
Совсем по-другому ведут себя проводники, помещенные электрическое поле. Заряды распределяются по их поверхности, образуя некий электрический потенциал. Если поверхность ровная, как у палочки, то заряды распределятся равномерно. Под действием внешнего электрического поля в проводнике происходит такое распределение электронов, чтобы внутри его сохранялся баланс взаимной компенсации негативных и позитивных зарядов.
Внешнее электрическое поле притягивает электроны на поверхность проводника, компенсируя при этом положительные заряды ионов. По отношению к проводнику имеет место электростатическая индукция, а заряды на его поверхности называются индуцированными. При этом на концах проводника плотность зарядов будет несколько выше.
На металлическом шаре заряды распределяются равномерно по всей поверхности. Наличие полости любой конфигурации абсолютно не влияет на процесс распределения.
Однако, если проводник убрать из зоны действия поля, то его заряды перераспределятся таким образом, что он снова станет электрически нейтральным.
На рисунке 1 изображена схема заряженного разнополюсного диэлектрика и проводника, удалённого из зоны действия электростатического поля. Благодаря тому, что диэлектрик сохраняет полученные заряды, уединенный проводник восстановил свою нейтральность.
 Рис. 1. Распределение зарядов
Рис. 1. Распределение зарядов
Интересное явление наблюдается с двумя проводниками, разделенными диэлектриком. Если одному из них сообщить положительный заряд, а другому – отрицательный, то после убирания источника электризации заряды на поверхности проводников сохранятся. Заряженные таким образом проводники обладают разностью потенциалов.
Заряды, накопившиеся на диэлектрике, уравновешивают внутренние взаимодействие в каждом из проводников, не позволяя им разрядиться. Величина заряда зависит от площади поверхности параллельных проводников и от свойства диэлектрика, расположенного между ними.
Свойство сохранять накопленный заряд называется электроемкостью. Точнее говоря, – это характеристика проводника, физическая величина определяющая меру его способности в накоплении электрического заряда.
Накопленное электричество можно снять с проводников путем короткого замыкания их или через нагрузку. С целью увеличения емкости на практике применяют параллельные пластины или же длинные полоски тонкой фольги, разделённой диэлектриком. Полоски сворачивают в тугой цилиндр для уменьшения объема. Такие конструкции называют конденсаторами.
На рисунке 2 изображена схема простейшего конденсатора с плоскими обкладками.
 Рис. 2. Схема простого конденсатора
Рис. 2. Схема простого конденсатора
Существуют конденсаторы других типов:
- переменные;
- электролитические;
- оксидные;
- бумажные;
- комбинированные и другие.
Важной характеристикой конденсатора, как и других накопительных систем, является его электрическая емкость.
Формулы
На рисунке 3 наглядно показано формулы для определения емкости, в т. ч. и для сферы.
 Рис. 3. Электроёмкость проводника
Рис. 3. Электроёмкость проводника
По отношению к конденсатору, для определения его емкости применяют формулу: C = q/U. То есть, эта величина прямо пропорциональна заряду одной из обкладок и обратно пропорциональна разнице потенциалов между обкладками (см. рис. 4).
 Ёмкость конденсатора
Ёмкость конденсатора
О других способах определения ёмкости конденсатора читайте в нашей статье: https://www.asutpp.ru/kak-opredelit-emkost-kondensatora.html
Единицы измерения
За единицу измерения величины электроемкости принято фараду: 1 Ф = 1 Кл/1В. Поскольку фарада величина огромная, то для измерения емкости на практике она мало пригодна. Поэтому используют приставки:
- мили (м) = 10-3;
- микро (мк) = 10-6;
- нано (н) = 10-9;
- пико (пк) = 10-12;
Например, электрическая емкость 1 мкф = 0,000001 Ф. Параметр зависит от геометрических размеров, конфигурации проводника и материала диэлектрика.
Уединенный проводник и его емкость
Уединенным называют проводник, влиянием на который других элементов цепей можно пренебречь. Предполагается, что все другие проводники бесконечно удалены от него, а как известно, потенциал точки, бесконечно удаленной в пространстве, равен 0.
Электрическую емкость C уединенного проводника, определяют как количество электричества q, которое требуется для повышения электрического потенциала на 1 В: С = q/ϕ. Параметр не зависит от материала, из которого изготовлен проводник.
Конденсаторы постоянной и переменной емкости
Эра накопителей электричества началась с воздушных конденсаторов. Благодаря плоскому конденсатору с большой площадью обкладок физики смогли понять, как взаимная емкость регулируется площадями пластин, что позволило им создать конденсаторы с переменной емкостью (см. рис. 5).
 Рис. 5. Конденсатор переменной емкости
Рис. 5. Конденсатор переменной емкости
Идея изменения емкости состояла в том, чтобы путем поворота плоской обкладки изменять площадь поверхности, которая располагается напротив другой пластины. Если обкладки располагались точно друг против друга, то напряженность поля между ними была максимальной. При смещении одной из пластин на некоторый угол, напряженность уменьшалась, что приводило к изменению емкости. Таким образом, можно было плавно управлять накопительной способностью конденсатора.
Детали с переменной емкостью нашли применение в первых радиоприемниках для поиска частоты нужной станции. Данный принцип используется по сегодняшний день в различных аналоговых электрических схемах.
Большую популярность приобрели электролитические конденсаторы. В качестве одной из обкладок у них используется электролит, обладающий высокими показателями диэлектрической проницаемости. Благодаря диэлектрическим свойствам электролитов такие конденсаторы обладают большими емкостями.
Главные их преимущества электролитического конденсатора:
- высокие
показатели емкости при малом объеме; - применение в
цепях с постоянным током.
Недостатки:
- необходимо соблюдать полярность;
- ограниченный срок службы;
- чувствительность к повышенным напряжениям.
Высокую электрическую прочность имеют плоские конденсаторы, у которых в качестве диэлектрического материала применяется керамика. Они используются в цепях с переменным током и выдерживают большие напряжения.
Сегодня промышленность поставляет на рынок множество конденсаторов различных типов, с высокими показателями проницаемости диэлектриков.
 Конденсаторы различных типов
Конденсаторы различных типов
Аккумуляторы и электроемкость
Накопители электричества большой емкости (аккумуляторы) состоят из положительных и негативных пластин, погруженных в электролит. Во время зарядки часть атомов электролита распадается на ионы, которые оседают на пластине. Образуется разность потенциалов между пластинами, что является причиной возникновения ЭДС при подключении нагрузки.
С целью увеличения напряжения аккумуляторы последовательно соединяют в батареи. Разница потенциалов одной секции около 2 В. Для получения аккумулятора на 6 В необходимо создать батарею из трех секций, а на 12 В – батарею из 6 секций.
Для характеристики аккумуляторов (батарей) используются параметры:
- емкости;
- номинального напряжения;
- максимального тока разряда.
Единицей емкости аккумулятора является ампер-час (А*ч) или кратные ей миллиампер-часы (мА*ч). Емкость аккумулятора зависит от площади пластин. Увеличить емкость можно путем параллельного подключения нескольких секций, но такой способ почти не применяется, так как проще и надежнее создать аккумулятор с большими пластинами.
Источник
Что такое электроемкость проводников
Если у нас есть два проводника, изолированных друг от друга, которым мы сообщаем некоторые заряды (обозначим их соответственно q1 и q2), то между ними возникнет определенная разность потенциалов. Ее величина будет зависеть от формы проводников, а также от исходных величин зарядов. Обозначим такую разность Δφ. Если мы говорим о разности, возникающей в электрическом поле между двумя точками, то ее обычно обозначают U.
В рамках темы данной статьи нам больше всего интересна такая разность потенциалов между проводниками, когда их заряды противоположны по знаку, но равны друг другу по модулю. В таком случае мы можем ввести новое понятие – электрическая емкость (электроемкость).
Определение 1
Электрической емкостью системы, состоящей из двух проводников, называется отношение заряда одного проводника (q) к разности потенциалов между этими двумя проводниками.
В виде формулы это записывается так: C=q∆φ=qU.
Для измерения электрической емкости применяется единица, называемая фарад. Она обозначается буквой Ф.
1Φ=1 Кл1 В.
Конфигурации и размеры проводников, а также свойства диэлектрика определяют величину электроемкости заданной системы. Наибольший интерес для нас представляют проводники особой формы, называемые конденсаторами.
Определение 2
Конденсатор – это проводник, конфигурация которого позволяет локализовать (сосредотачивать) электрическое поле в одной выделенной части пространства. Проводники, составляющие конденсатор, называются обкладками.
Определение 3
Если мы возьмем две плоские пластины из проводящего материала, расположим их на небольшом расстоянии друг от друга и проложим между ними слой диэлектрика, то мы получим простейший конденсатор, называемый плоским. При его работе электрическое поле будет располагаться преимущественно в промежутке между пластинами, но небольшая часть этого поля будет рассеиваться вокруг них.
Определение 4
Часть электрического поля вблизи конденсатора называется полем рассеяния.
Иногда в задачах мы можем не учитывать его и работать только с той частью электрического поля, которое расположено между обкладками. Однако пренебрегать полем рассеяния допустимо далеко не всегда, поскольку это может привести к ошибочным расчетам из-за нарушения потенциального характера электрического поля.
Рисунок 1.6.1. Электрическое поле в плоском конденсаторе.
Рисунок 1.6.2. Электрическое поле конденсатора без учета поля рассеяния, не обладающее потенциальностью.
Модуль напряженности электрического поля, которое создает каждая обкладка в плоском конденсаторе, выражается соотношением следующего вида:
E1=σ2ε0.
Исходя из принципа суперпозиции, можно утверждать, что напряженность E→ поля, которое создают обе пластины конденсатора, будет равна сумме напряженностей E+→ и E-→ полей каждой пластины, то есть E→=E+→+E-→.
Векторы напряженностей обеих пластин во внутренней части конденсатора будут параллельны друг другу. Значит, мы можем выразить модуль напряженности их суммарного поля в виде формулы E=2E1=σε0.
Как рассчитать электроемкость конденсатора
Вне пластин векторы напряженности будут направлены в противоположные друг от друга стороны, значит, E будет равно нулю. Если мы обозначим заряд каждой обкладки как q, а ее площадь как S, то соотношение qS даст нам представление о поверхностной плотности. Умножив E на расстояние между обкладками (d), мы получим разность потенциалов между пластинами в однородном электрическом поле. Теперь возьмем оба этих соотношения и выведем из них формулу, по которой может быть рассчитана электрическая емкость конденсатора.
C=q∆φ=σ·SE·d=ε0Sd.
Определение 5
Электрическая емкость плоского конденсатора – величина, обратно пропорциональная расстоянию между обкладками и прямо пропорциональная их площади.
Заполнение пространства между проводниками диэлектрическим материалом может увеличить электроемкость плоского конденсатора в число раз, кратное undefined.
Определение 6
Введем обозначение емкости в виде буквы С и запишем это в виде формулы:
C=εε0Sd.
Данная формула называется формулой электроемкости плоского конденсатора.
Конденсаторы бывают не только плоскими. Возможны и другие конфигурации, также обладающие специфическими свойствами.
Определение 7
Сферическим конденсатором называется система из 2-х концентрических сфер, сделанных из проводящего материала, радиусы которых равны R1 и R2 соответственно.
Определение 8
Цилиндрическим конденсатором называется системы из двух проводников цилиндрической формы, длина которых равна L, а радиусы R1 и R2.
Обозначим проницаемость диэлектрического материала как ε и запишем формулы, по которым можно найти электрическую емкость конденсаторов:
- C=4πε0εR1R2R2-R1(сферический конденсатор),
- C=2πε0εLlnR2R1(цилиндрический конденсатор).
Как рассчитать электроемкость батареи конденсаторов
Определение 9
Если мы соединим несколько проводников между собой, то мы получим конструкцию, называемую батареей.
Способы соединения могут быть разными. Если соединение будет параллельным, то напряжение всех конденсаторов в системе будет одинаково: U1=U2 =U, а заряды можно найти по формулам q1=С1U и q2=C2U. При таком соединении вся система может считаться одним конденсатором, электроемкость которого равна C, заряд – q=q1+q2, а напряжение – U. В виде формулы это выглядит так:
С=q1+q2U или C=C1+C2
Определение 10
Если в батарее конденсаторов элементы соединены параллельно, то для нахождения общей электроемкости нам нужно сложить емкости ее отдельных элементов.
Рисунок 1.6.3. Конденсаторы, соединенные параллельно. C=C1+C2
Рисунок 1.6.4. Конденсаторы, соединенные последовательно: 1C=1C1+1C2
Если же батарея состоит из двух последовательно соединенных конденсаторов, то заряды обоих будут одинаковы: q1=q2=q. Найти их напряжения можно так: U1=qC1 и U2=qC2. Такую систему тоже можно считать одним конденсатором, заряд которого равен q, а напряжение U=U1+U2.
C=qU1+U2 или 1C=1C1+1C2
Определение 11
Если конденсаторы в батарее соединены последовательно, то для нахождения общей электроемкости нам нужно сложить величины, обратные емкостям каждого из них.
Справедливость обеих формул, приведенных выше, не зависит от количества конденсаторов в батарее.
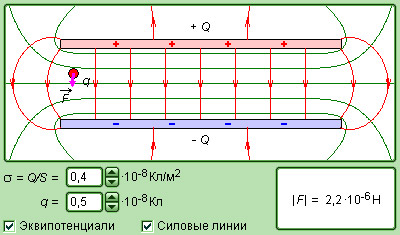
Рисунок 1.6.5. Смоделированное электрическое поле плоского конденсатора.
Источник
Определение 1
Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.
Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:
C=qφ1-φ2=qU.
Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.
Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.
Плоский конденсатор
Определение 2
Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.
Формула для расчета электроемкости записывается как
C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε – диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.
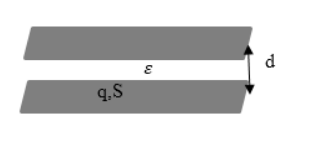
Рисунок 1
При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:
C=ε0Sd1ε1+d2ε2+…+dNεN.
Сферический конденсатор
Определение 3
Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.
Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2. Емкость рассчитывается по формуле:
C=4πεε0R1R2R2-R1, где R1 и R2 являются радиусами обкладок.
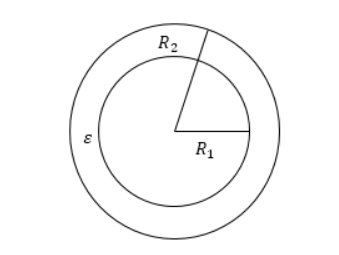
Рисунок 2
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равняется:
C=2πεε0llnR2R1, где l – высота цилиндров, R1 и R2 – радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3.
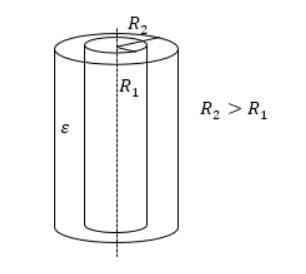
Рисунок 3
Определение 4
Важной характеристикой конденсаторов считается пробивное напряжение – напряжение, при котором происходит электрический разряд через слой диэлектрика.
Umax находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Электроемкость плоского конденсатора. Формулы
Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы Ci, где Ci- это емкость конденсатора с номером i:
C=∑i=1NCi.
При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:
Пример 1
Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 см2 с расстоянием между ними 1 мм. Пространство между обкладками находится в вакууме.
Решение
Чтобы рассчитать электроемкость конденсатора, применяется формула:
C=εε0Sd.
Значения:
ε=1, ε0=8,85·10-12 Фм;S=1 см2=10-4 м2;d=1 мм=10-3 м.
Подставим числовые выражения и вычислим:
C=8,85·10-12·10-410-3=8,85·10-13 (Ф).
Ответ: C≈0,9 пФ.
Пример 2
Найти напряженность электростатического поля у сферического конденсатора на расстоянии x=1 см=10-2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R1=1 см=10-2 м, внешнем – R2=3 см=3·10-2 м. Значение напряжения – 103 В.
Решение
Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:
E=14πεε0qr2, где q обозначают заряд внутренней сферы, r=R1+x – расстояние от центра сферы.
Нахождение заряда предполагает применение определения емкости конденсатора С:
q=CU.
Для сферического конденсатора предусмотрена формула вида
C=4πεε0R1R2R2-R1 с радиусами обкладок R1 и R2.
Производим подстановку выражений для получения искомой напряженности:
E=14πεε0U(x+R1)24πεε0R1R2R2-R1=U(x+R1)2R1R2R2-R1.
Данные представлены в системе СИ, поэтому достаточно заменить буквы числовыми выражениями:
E=103(1+1)2·10-4·10-2·3·10-23·10-2-10-2=3·10-18·10-6=3,45·104 Вм.
Ответ: E=3,45·104 Вм.
Источник
