Какое свойство движения характеризует ускорение

Механика – раздел физики, в котором изучают механическое движение.
Механику подразделяют на кинематику, динамику и статику.
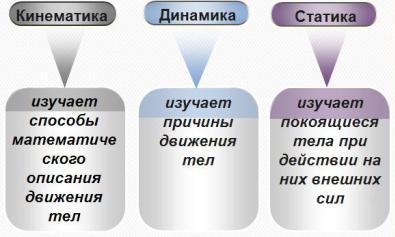
Кинематикойназывают раздел механики, в котором движение тел рассматривается без выяснения причин этого движения. Кинематика изучает способы описания движения и связь между величинами, характеризующими эти движения.
Задача кинематики: определение кинематических характеристик движения (траектории движения, перемещения, пройденного пути, координаты, скорости и ускорения тела), а также получение уравнений зависимости этих характеристик от времени.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Механическое движение относительно, выражение «тело движется» лишено всякого смысла, пока не определено, относительно чего рассматривается движение. Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета. Покой тоже относителен (примеры: пассажир в покоящемся поезде смотрит на проходящий мимо поезд)
Главная задача механики – уметь вычислять координаты точек тела в любой момент времени.
Чтобы решить эту надо иметь тело, от которого ведется отсчет координат, связать с ним систему координат и иметь прибор для измерения промежутков времени.
Система координат, тело отсчета, с которым она связана, и прибор для отсчета времени образуют систему отсчета, относительно которой и рассматривается движение тела.
Системы координат бывают:
1. одномерная – положение тела на прямой определяется одной координатой x.

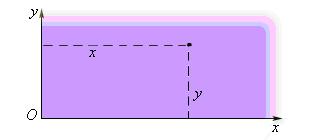
2. двумерная – положение точки на плоскости определяется двумя координатами x и y.
3. трехмерная – положение точки в пространстве определяется тремя координатами x, y и z.
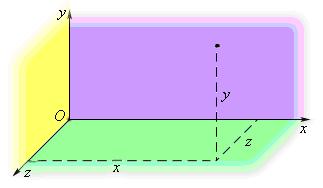
Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.
Если все части тела движутся одинаково, то такое движение называется поступательным.
Поступательно движутся, например, кабины в аттракционе «Гигантское колесо», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.
Материальной точкой называется тело, размерами которого в данных условиях можно пренебречь.
Понятие материальной точки играет важную роль в механике. Тело можно рассматривать как материальную точку, если его размеры малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстоянием от него до других тел.
Пример. Размеры орбитальной станции, находящейся на орбите около Земли, можно не учитывать, а рассчитывая траекторию движения космического корабля при стыковке со станцией, без учета ее размеров не обойтись.
Характеристики механического движения: перемещение, скорость, ускорение.
Механическое движение характеризуется тремя физическими величинами: перемещением, скоростью и ускорением.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.
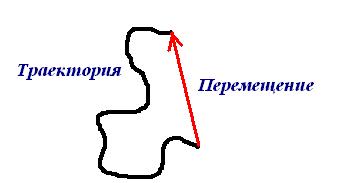
Линия, по которой движется точка тела, называется траекторией движения.
Длина траектории называется пройденным путем.
Обозначается l, измеряется в метрах. (траектория – след, путь – расстояние)
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.
Вектор, соединяющий начальную и конечную точки траектории, называется перемещением.
Обозначается S, измеряется в метрах.(перемещение – вектор, модуль перемещения – скаляр)
Скорость – векторная физическая величина, характеризующая быстроту перемещения тела, численно равная отношению перемещения за малый промежуток времени к величине этого промежутка.
Обозначается v
Формула скорости: 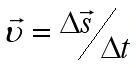 или
или 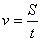
Единица измерения в СИ – м/с.
На практике используют единицу измерения скорости км/ч (36 км/ч = 10 м/с).
Измеряют скорость спидометром.
Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле:
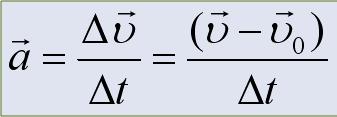
Ускорение измеряют акселерометром
Единица измерения в СИ м/с2
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение , скорость и ускорение . Путь l является скалярной величиной. Перемещение , скорость и ускорение – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.
Проверить свои знания (тест по теме “Механическое движение, его характеристики”)
Источник
Механика — раздел физики, который изучает механическое движение физических тел и взаимодействие между ними.
Основная задача механики — определение положение тела в пространстве в любой момент времени.
Механическое движение — изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение и его виды
По характеру движения точек тела выделяют три вида механического движения:
- Поступательное. Это движение, при котором все точки тела движутся одинаково. Если через тело мысленно провести прямую, то после изменения положения этого тела в пространстве данная прямая останется параллельной самой себе.
- Вращательное. Это движение, при котором все точки тела движутся, описывая окружности.
- Колебательное. Это движение тела, которое повторяется точно или приблизительно через определенные интервалы времени. От вращательного движения его отличает то, что при колебаниях тело перемещается в двух взаимно противоположных направлениях.
По типу линии, вдоль которой движется тело, выделяют два вида движения:
- Прямолинейное — тело движется по прямой линии.
- Криволинейное — тело движется по кривой линии, в том числе замкнутой.
По скорости выделяют два вида движения:
- Равномерное — скорость движущегося тела остается неизменной.
- Неравномерное — скорость движущегося тела с течением времени меняется.
По ускорению выделяют три вида движения:
- Равноускоренное — тело движется неравномерно с постоянным ускорением (положительным). Скорость увеличивается.
- Равнозамедленное — тело движется неравномерно с постоянным замедлением (отрицательным ускорением). Скорость уменьшается.
- Ускоренное — тело движется неравномерно с меняющимся ускорением. Скорость может, как увеличиваться, так и уменьшаться.
Что нужно для описания механического движения?
Для описания механического движения нужно выбрать, относительно какого тела оно будет рассматриваться. Движение одного и того же объекта относительно разных тел неодинаковое. К примеру, идущий человек относительно дерева движется с некоторой скоростью. Но относительно сумки, которую он держит в руках, он находится в состоянии покоя, так как расстояние между ними с течением времени не изменяется.
Решение основной задачи механики — определения положения тела в пространстве в любой момент времени — заключается в вычислении координат его точек. Чтобы вычислить координаты тела, нужно ввести систему координат и связать с ней тело отсчета. Также понадобится прибор для измерения времени. Все это вместе составляет систему отсчета.
Система отсчета — совокупность тела отсчета и связанных с ним системы координат и часов.
Тело отсчета — тело, относительно которого рассматривается движение.
Часы — прибор для отсчета времени. Время измеряется в секундах (с).
При описании движения тела важно учитывать его размеры, так как характер движения его отдельных точек может различаться. Но в рамках некоторых задач размер тела не влияет на результат решения. Тогда его можно считать пренебрежительно малым. Тогда тело рассматривают как движущуюся материальную точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях конкретной задачи. Допустимо принимать тело за точку, если оно движется поступательно или его размеры намного меньше расстояний, которые оно проходит.
Виды систем координат
В зависимости от характера движения тела для его описания выбирают одну из трех систем координат:
- Одномерную. Используется, когда положение материальной точки можно задать только одной координатой x — M(x) . В этом случае тело движется прямолинейно.
- Двумерную. Используется, когда положение материальной точки можно задать двумя координатами x и y — M(x,y). Тело в этом случае движения по плоскости.
- Трехмерную. Используется, когда положение материальной точки можно задать тремя координатами x, y и z — M(x,y,z). Тело в этом случае изменяет положение в трехмерном пространстве.
Способы описания механического движения
Описать механическое движение можно двумя способами:
- координатным
- векторным
Координатный способ
Указать положение материальной точки в пространстве можно, используя трехмерную систему координат. Если эта точка движется, то ее координаты с течением времени меняются. Так как координаты точки зависят от времени, можно считать, что они являются функциями времени. Математически это записывается так:
Эти уравнения называют кинематическими уравнениями движения точки, записанными в координатной форме.
Векторный способ
Радиус-вектор точки — вектор, начало которого совпадает с началом системы координат, а конец — с положением этой точки.
Указать положение точки в трехмерном пространстве также можно с помощью радиус-вектора. При движении точки радиус-вектор со временем изменяется. Он может менять направление и длину. Это значит, что радиус-вектор тоже можно принять за функцию времени. Математически это записывается так:
Эта формула называется кинематическим уравнением движения точки, записанным в векторной форме.
Характеристики механического движения
Движение материальной точки характеризуют три физические величины:
- перемещение
- скорость
- ускорение
Перемещение
Определение
Перемещение (вектор перемещения) — направленный отрезок, начало которого совпадает с начальным положением точки, а конец — с его конечным положением. Обозначается как S.
Перемещение точки определяется как изменение радиус-вектора. Это изменение обозначается как Δr. С точки зрения геометрии вектор перемещения равен разности радиус-векторов, задающих конечное и начальное положение точки:
Траектория — линия, которую описывает тело во время движения.
Путь — длина траектории. Обозначается буквой s. Единица измерения — метры (м).
Путь есть функция времени:
Модуль перемещения — длина вектора перемещения. Обозначается как |Δr|. Единица измерения — метры (м).
Внимание!
Модуль перемещения необязательно должен совпадать с длиной пути.
Пример №1. Человек обошел круглое поле диаметром 1 км. Чему равны пройденный путь и перемещение, которое он совершил.
Путь равен длине окружности. Поэтому:
Человек, обойдя круглое поле, вернулся в ту же точку. Поэтому его начальное положение совпадает с конечным. В этом случае человек совершил перемещение, равное нулю.
Пример №2. Точка движется по окружности радиусом 10 м. Чему равен путь, пройденный этой точкой, в момент, когда модуль перемещения равен диаметру окружности?
Диаметр — это отрезок, который соединяет две точки окружности и проходит через центр. Перемещение равно длине этого отрезка в случае, если один из концов этого отрезка является началом вектора перемещения, а другой — его концом. Траекторией движения в этом случае является дуга, равная половине окружности. А длина траектории есть путь:
Скорость
Определение
Скорость — векторная физическая величина, характеризующая быстроту перемещения тела. Численно она равна отношению перемещения за малый промежуток времени к величине этого промежутка.
В физике скорость обозначается V. Математически скорость определяется формулой:
Скорость характеризуется не только направлением вектора скорости, но и его модулем.
Модуль скорости — расстояние, пройденное точкой за единицу времени. Обозначается буквой V и измеряется в метрах в секунду (м/с).
Математическое определение модуля скорости:
Величина скорости тела в данный момент времени есть первая производная от пройденного пути по времени:
Ускорение
Определение
Ускорение — векторная физическая величина, которая характеризует быстроту изменения скорости тела. Численно она равна отношению изменения скорости за малый промежуток времени к величине этого промежутка.
В физике ускорение обозначается a. Математически оно определяется формулой:
Модуль ускорения — численное изменение скорости в единицу времени. Обозначается буквой a. Единица измерения — метры в секунду в квадрате (м/с2).
Математическое определение модуля скорости:
v — скорость тела в данный момент времени, v0— его скорость в начальный момент времени, t — время, в течение которого эта скорость менялась.
Ускорение тела есть первая производная от скорости или вторая производная от пройденного пути по времени:
Проекция вектора перемещения на ось координат
Определение
Проекция вектора перемещения на ось — это скалярная величина, численно равная разности конечной и начальной координат.
Проекция вектора на ось OX:
Проекция вектора на ось OY:
Знаки проекций перемещения
- Проекция является положительной, если движение от начала проекции вектора к проекции конца происходит сонаправленно оси координат.
- Проекция является отрицательной, если движение от начала проекции вектора к проекции конца направлено в сторону, противоположную направлению координатной оси.
Внимание!
Проекция вектора перемещения на ось считается нулевой, если вектор расположен перпендикулярно этой оси.
Модуль перемещения — длина вектора перемещения:
Модуль перемещения измеряется в метрах (м).
Вместе с собственными проекциями модуль перемещения образует прямоугольный треугольник. Сам он является гипотенузой этого треугольника. Поэтому для его вычисления можно применить теорему Пифагора. Выглядит это так:
Выразив проекции вектора перемещения через координаты, эта формула примет вид:
Выражение проекций вектора перемещения через угол его наклона по отношению к координатным осям:
Общий вид уравнений координат:
Пример №3. Определить проекции вектора перемещения на ось OX, OY и вычислить его модуль.
Определяем координаты начальной точки вектора:
Определяем координаты конечной точки вектора:
Проекция вектора перемещения на ось OX:
Проекция вектора перемещения на ось OY:
Применяем формулу для вычисления модуля вектора перемещения:
Пример №4. Определить координаты конечной точки B вектора перемещения, если начальная точка A имеет координаты (–5;5). Учесть, что проекция перемещения на OX равна 10, а проекция перемещения на OY равна 5.
Извлекаем известные данные:
Для определения координаты точки В понадобятся формулы:
Выразим из них координаты конечного положения точки:
Точка В имеет координаты (5; 10).
Алгоритм решения
- Записать исходные данные в определенной системе отсчета.
- Записать формулу ускорения.
- Выразить из формулы ускорения скорость.
- Найти искомую величину.
Решение
Записываем исходные данные:
- Тело начинает двигаться из состояния покоя. Поэтому его начальная скорость v0 = 0 м/с.
- Ускорение, с которым тело начинает движение, равно: a = 4 м/с2.
- Время движения согласно условию задачи равно: t = 2 c.
Записываем формулу ускорения:
Так как начальная скорость равна 0, эта формула принимает вид:
Отсюда скорость равна:
v = at
Подставляем имеющиеся данные и вычисляем:
v = 4∙2 = 8 (м/с)
Ответ: 8
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | ???? Скачать PDF |
Источник
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: механическое движение и его виды, относительность механического движения, скорость, ускорение.
Понятие движения является чрезвычайно общим и охватывает самый широкий круг явлений. В физике изучают различные виды движения. Простейшим из них является механическое движение. Оно изучается в механике.
Механическое движение — это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.
Если тело A меняет своё положение относительно тела B, то и тело B меняет своё положение относительно тела A. Иначе говоря, если тело A движется относительно тела B, то и тело B движется относительно тела A. Механическое движение является относительным — для описания движения необходимо указать, относительно какого тела оно рассматривается.
Так, например, можно говорить о движении поезда относительно земли, пассажира относительно поезда, мухи относительно пассажира и т. д. Понятия абсолютного движения и абсолютного покоя не имеют смысла: пассажир, покоящийся относительно поезда, будет двигаться с ним относительно столба на дороге, совершать вместе с Землёй суточное вращение и двигаться вокруг Солнца.
Тело, относительно которого рассматривается движение, называется телом отсчёта.
Основной задачей механики является определение положения движущегося тела в любой момент времени. Для решения этой задачи удобно представить движение тела как изменение координат его точек с течением времени. Чтобы измерить координаты, нужна система координат. Чтобы измерять время, нужны часы. Всё это вместе образует систему отсчёта.
Система отсчёта — это тело отсчёта вместе с жёстко связанной с ним («вмороженной»» в него) системой координат и часами.
Система отсчёта показана на рис. 1. Движение точки рассматривается в системе координат . Начало координат является телом отсчёта.
 |
| Рисунок 1. |
Вектор называется радиус-вектором точки . Координаты точки являются в то же время координатами её радиус-вектора .
Решение основной задачи механики для точки состоит в нахождении её координат как функций времени: .
В ряде случаев можно отвлечься от формы и размеров изучаемого объекта и рассматривать его просто как движущуюся точку.
Материальная точка — это тело, размерами которого можно пренебречь в условиях данной задачи.
Так, поезд можно считать материальной точкой при его движении из Москвы в Саратов, но не при посадке в него пассажиров. Землю можно считать материальной точкой при описании её движения вокруг Солнца, но не её суточного вращения вокруг собственной оси.
К характеристикам механического движения относятся траектория, путь, перемещение, скoрость и ускорение.
Траектория, путь, перемещение.
В дальнейшем, говоря о движущемся (или покоящемся) теле, мы всегда полагаем, что тело можно принять за материальную точку. Случаи, когда идеализацией материальной точки пользоваться нельзя, будут специально оговариваться.
Траектория — это линия, вдоль которой движется тело. На рис. 1 траекторией точки является синяя дуга, которую описывает в пространстве конец радиус-вектора .
Путь — это длина участка траектории, пройденного телом за данный промежуток времени.
Перемещение — это вектор, соединяющий начальное и конечное положение тела.
Предположим, что тело начало движение в точке и закончило движение в точке (рис. 2). Тогда путь, пройденный телом, это длина траектории . Перемещение тела — это вектор .
 |
| Рисунок 2. |
Скорость и ускорение.
Рассмотрим движение тела в прямоугольной системе координат с базисом (рис. 3).
 |
| Рисунок 3. |
Пусть в момент времени тело находилось в точке с радиус-вектором
Спустя малый промежуток времени тело оказалось в точке с
радиус-вектором
Перемещение тела:
(1)
Мгновенная скорость в момент времени – это предел отношения перемещения к интервалу времени , когда величина этого интервала стремится к нулю; иными словами, скорость точки – это производная её радиус-вектора:
(2)
Из (2) и (1) получаем:
Коэффициенты при базисных векторах в пределе дают производные:
(Производная по времени традиционно обозначается точкой над буквой.) Итак,
Мы видим, что проекции вектора скорости на координатные оси являются производными координат точки:
Когда стремится к нулю, точка приближается к точке и вектор перемещения разворачивается в направлении касательной. Оказывается, что в пределе вектор направлен точно по касательной к траектории в точке . Это и показано на рис. 3.
Понятие ускорения вводится похожит образом. Пусть в момент времени скорость тела равна , а спустя малый интервал скорость стала равна .
Ускорение – это предел отношения изменения скорости к интервалу , когда этот интервал стремится к нулю; иначе говоря, ускорение – это производная скорости:
Ускорение, таким образом, есть “cкорость изменения скорости”. Имеем:
Следовательно, проекции ускорения являются производными проекций скорости (и, стало быть, вторыми производными координат):
Закон сложения скоростей.
Пусть имеются две системы отсчёта. Одна из них связана с неподвижным телом отсчёта . Эту систему отсчёта обозначим и будем называть неподвижной.
Вторая система отсчёта, обозначаемая , связана с телом отсчёта , которое движется относительно тела со скоростью . Эту систему отсчёта называем движущейся. Дополнительно предполагаем, что координатные оси системы перемещаются параллельно самим себе (нет вращения системы координат), так что вектор можно считать скоростью движущейся системы относительно неподвижной.
Неподвижная система отсчёта обычно связана с землёй. Если поезд плавно едет по рельсам со скоростью , это система отсчёта, связанная с вагоном поезда, будет движущейся системой отсчёта .
Заметим, что скорость любой точки вагона (кроме вращающихся колёс!) равна . Если муха неподвижно сидит в некоторой точке вагона, то относительно земли муха движется со скоростью . Муха переносится вагоном, и потому скорость движущейся системы относительно неподвижной называется переносной скоростью.
Предположим теперь, что муха поползла по вагону. Скорость мухи относительно вагона (то есть в движущейся системе ) обозначается и называется относительной скоростью. Скорость мухи относительно земли (то есть в неподвижной системе ) обозначается и называется абсолютной скоростью.
Выясним, как связаны друг с другом эти три скорости – абсолютная, относительная и переносная.
На рис. 4 муха обозначена точкой .Далее:
– радиус-вектор точки в неподвижной системе ;
– радиус-вектор точки в движущейся системе ;
– радиус-вектор тела отсчёта в неподвижной системе .
 |
| Рисунок 4. |
Как видно из рисунка,
Дифференцируя это равенство, получим:
(3)
(производная суммы равна сумме производных не только для случая скалярных функций, но и для векторов тоже).
Производная есть скорость точки в системе , то есть абсолютная скорость:
.
Аналогично, производная есть скорость точки в системе , то есть относительная скорость:
А что такое ? Это скорость точки в неподвижной системе, то есть – переносная скорость движущейся системы относительно неподвижной:
В результате из (3) получаем:
Закон сложения скоростей. Скорость точки относительно неподвижной системы отсчёта равна векторной сумме скорости движущейся системы и скорости точки относительно движущейся системы. Иными словами, абсолютная скорость есть сумма переносной и относительной скоростей.
Таким образом, если муха ползёт по движущемуся вагону, то скорость мухи относительно земли равна векторной сумме скорости вагона и скорости мухи относительно вагона. Интуитивно очевидный результат!
Виды механического движения.
Простейшими видами механического движения материальной точки являются равномерное и прямолинейное движения.
Движение называется равномерным, если модуль вектора скорости остаётся постоянным (направление скорости при этом может меняться).
Движение называется прямолинейным, если направление вектора скорости остаётся постоянным (а величина скорости при этом может меняться). Траекторией прямолинейного движения служит прямая линия, на которой лежит вектор скорости.
Например, автомобиль, который едет с постоянной скоростью по извилистой дороге, совершает равномерное (но не прямолинейное) движение. Автомобиль, разгоняющийся на прямом участке шоссе, совершает прямолинейное (но не равномерное) движение.
А вот если при движении тела остаются постоянными как модуль скорости, так и его направление, то движение называется равномерным прямолинейным.
В терминах вектора скорости можно дать более короткие определения данным типам движения:
Важнейшим частным случаем неравномерного движения является равноускоренное движение, при котором остаются постоянными модуль и направление вектора ускорения:
- равноускоренное движение
Наряду с материальной точкой в механике рассматривается ещё одна идеализация – твёрдое тело.
Твёрдое тело – это система материальных точек, расстояния между которыми не меняются со временем. Модель твёрдого тела применяется в тех случаях, когда мы не можем пренебречь размерами тела, но можем не принимать во внимание изменение размеров и формы тела в процессе движения.
Простейшими видами механического движения твёрдого тела являются поступательное и вращательное движения.
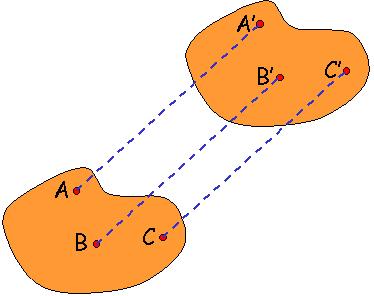
Движение тела называется поступательным, если всякая прямая, соединяющая две какие-либо точки тела, перемещается параллельно своему первоначальному направлению. При поступательном движении траектории всех точек тела идентичны: они получаются друг из друга параллельным сдвигом (рис. 5).
 |
| Рисунок 5. |
Движение тела называется вращательным, если все его точки описывают окружности, лежащие в параллельных плоскостях. При этом центры данных окружностей лежат на одной прямой, которая перпендикулярна всем этим плоскостям и называется осью вращения.
На рис. 6 изображён шар, вращающийся вокруг вертикальной оси. Так обычно рисуют земной шар в соответствующих задачах динамики.
 |
| Рисунок 6. |
Источник
