Какое свойство для сочетаний

Комбинаторика
Комбинаторика располагает столь многообразными методами, решает столь разнообразные задачи, что трудно чётко обозначить её границы. Условно в комбинаторной теории можно выделить следующие три большие части (см. схему):
- Теорию конфигураций, включающую блок – схемы, группы подстановок, теорию кодирования.
- Теорию перечисления, содержащую производящие функции, теоремы обращения и исчисление конечных разностей.
- Теорию порядка, включающую конечные упорядоченные множества и решётки, матрицы и теоремы существования, подобные теоремам Холла и Рамсея.
Следует ещё раз подчеркнуть в высшей степени условный характер представленной схемы. Повсеместно можно наблюдать взаимную связь перечисленных разделов комбинаторики. Например, перечислительная комбинаторика рассматривает задачи, относящиеся и к конфигурациям, и к упорядоченным множествам.
Теория конфигураций и теория перечисления
Теория конфигураций является традиционным и наиболее разработанным разделом комбинаторики. Теория конфигураций рассматривает задачи выбора и расположения элементов некоторого, обычно конечного, множества, в соответствии с заданными правилами. Перечислительная комбинаторика основным методом исследования провозгласила метод производящих функций, используя который было доказано громадное число комбинаторных тождеств.
Элементарными комбинаторными конфигурациями являются сочетания, размещения, перестановки. Для подсчёта числа этих конфигураций используются правила суммы и произведения.
Правило суммы:
Если элемент A можно выбрать m способами, а элемент B можно выбрать k способами, то выбор элемента A или B можно осуществить m + k способами.
Правило суммы можно перефразировать на теоретико-множественном языке. Обозначим через | A | число элементов множества A, через A B – объединение множеств A и B, через AxB – декартово произведение множеств A и B. Тогда для непересекающихся множеств A и B выполняется равенство:
| A B | = | A | + | B |.
Обобщением правила суммы является правило произведения.
Правило произведения:
Если элемент A можно выбрать m способами, а после каждого выбора элемента A элемент B можно выбрать k способами, тогда, упорядоченную пару элементов (A, B) можно выбрать m*kспособами.
Правило произведения можно распространить на выбор последовательности (x1, x2, …, xn) произвольной конечной длины n.
На теоретико-множественном языке правило произведения формулируется так: | Aх B | = | A | | B |.
Размещения.
Назовём множество, содержащее n элементов, n-множеством.
Последовательность (x1, x2, …, xk ) длины k без повторяющихся элементов из элементов данного n-множества назовём k-размещением.
Обозначим символом число размещений из n по k элементов (от фран. “arrangement” – размещение). Используя правило произведения, вычислим число .
Пусть произвольное размещение длины k имеет вид:
(x1, x2, …, xk ).
Элемент x1 можно выбрать n способами. После каждого выбора x1 элемент x2 можно выбрать
(n – 1) способами. После каждого выбора элементов x1 и x2 элемент x3 можно выбрать (n – 2) способами, и т.д. После каждого выбора элементов x1, x2, …, xk-1 элемент xk можно выбрать
(n – (k – 1)) = (n – k + 1) способами. Тогда, по правилу произведения, последовательность
(x1; x2; , …, xk ) можно выбрать числом способов, равным
n(n – 1)(n – 2) … (n – k + 1) =
Произведение в левой части равенства умножим и разделим на (n – k)!, получим:
.
Если k = n, то есть число Pn перестановок из n элементов
Pn = n! (от “permutation”- перестановка).
Сочетания.
k-подмножество данного n-множества называется k-сочетанием.
Обозначим через число k-сочетаний из данных n элементов. Формулу для числа получим, рассуждая следующим образом. Если каждое сочетание упорядочить всеми возможными способами, то получим все k-последовательностей из n элементов, без повторений, то есть все k-размещения.
Иными словами,
Откуда:
или
Предполагая, что n и k – целые положительные числа и 0!=1, сформулируем основные свойства сочетаний.
Основные свойства сочетаний.
1. Условились, что
2.
3.
4.
5.
Сочетания и размещения широко используются при вычислении классической вероятности случайных событий.
Таблица 1.Треугольник Паскаля
Заметим, что Блез Паскаль называл числовой треугольник, начало которого содержится в таблице1, арифметическим. Паскаль посвятил свойствам арифметического треугольника основополагающий “Трактат об арифметическом треугольнике” (1654). Справедливости ради, стоит упомянуть, что биномиальные коэффициенты были хорошо известны в Азии за много веков до рождения Паскаля. В Италии треугольник Паскаля называют треугольником Тартальи.
Сочетания имеют многочисленные интерпретации и приложения. Сочетания являются биномиальными коэффициентами в разложении бинома
В этой интерпретации индексы могут принимать вещественные значения. Используя свойства биномиальных коэффициентов (при разных ограничениях на выбор верхних и нижних индексов), доказано громадное число комбинаторных тождеств, составивших самостоятельный раздел комбинаторной математики. В частности, из формулы выше при x = 1, получим , при
x = -1, n > 0, получим , продифференцировав равенство, получим при x = 1, и т.д.
Существует тесная связь между подмножествами множества и разложениями целого (положительного) числа. Разложение nесть представление числа n в виде упорядоченной суммы положительных целых чисел. Например, существует восемь разложений числа 4, именно:
1+1+1+1 3+1
2+1+1 1+3
1+2+1 2+2
1+1+2 4
Если разложение содержит в точности k слагаемых, то говорят, что имеет k частей и называется k-разложением. Для k-разложения числа n: a1 + a2 + …+ an – определим
(k – 1)-подмножество ( ), (n – 1)-множества {1, 2, …, n-1}, формулой.
( ) ={ a1, a1 + a2,…, a1 + a2 +…+ ak-1 }
Эта формула устанавливает биекцию между всеми k-разложениями числа n и (k – 1)-подмножествами (n – 1)-множества.
Следовательно, существует k-разложений числа n и 2n-1 разложений числа n. Биекцию часто схематично изображают строкой, состоящей из n точек и k – 1 разделяющей вертикальной черты. Точки разделились по k линейно упорядоченным “купе”; числа точек в “купе” соответствуют слагаемым в k-разложении числа n. Например, строка | | | | | соответствует разложению 1+2+1+1+3+2. Другая проблема, тесно связанная с разложениями, есть задача подсчёта числа N(n,k) решений уравнения
x1 + x2 + …+ xk = n
Неотрицательные целые решения уравнения называются слабыми k-разложениями числа n. Число неотрицательных целых решений уравнения равно числу положительных решений уравнения
y1 + y2 + … + yk = n + k,
то есть числу k-разложений числа n + k. Таким образом, N(n,k) = .
Если k-сочетание содержит повторяющиеся элементы, то такое k-сочетание называют
k-мультимножеством. Число всех k-сочетаний с повторениями из данного n-элементного множества обозначим через , где
Сочетание можно интерпретировать, как распределение элементов n-множества S между двумя категориями, первая из которых содержит k элементов, вторая содержит n – k элементов. Обобщим это представление. Пусть (a1, a2, …, am)- последовательность неотрицательных целых чисел, сумма которых равна n. Рассмотрим m категорий C1, C2, … Cm.
Обозначим символом
число способов распределения n элементов среди категорий C1, C2, … Cm так, чтобы категории Ci принадлежало точно ai элементов. Тогда
Блок-схемы
Комбинаторные конфигурации наиболее общего вида были исследованы в 30-е годы XX столетия и были названы блок-схемами (block design). Блок-схемы состоят из наборов элементов, называемых блоками. Выбор элементов и пар элементов в блоки подчиняются определённым правилам.
Уравновешенной неполной блок-схемой называется такое размещение v различных элементов по b блокам, что каждый блок содержит точно k различных элементов, каждый элемент появляется точно в k различных блоках и каждая пара различных элементов ai , ajпоявляется точно в блоках.
Множество всех сочетаний из v элементов по k, взятых в качестве блоков, образует полную блок-схему. Часть этих сочетаний, в которых каждая пара ai, aj появляется одно и то же число раз, является неполной, но уравновешенной блок-схемой. Между пятью параметрами блок-схемы выполняются следующие два соотношения:
bk = vr
r (k – 1) = (v – 1)
Частным случаем блок-схем являются так называемые конечные плоскости. Выберем конечное множество P. Элементы из P назовём точками. Некоторые подмножества из P назовём прямыми. Пусть отношение инцидентности между точками и прямыми удовлетворяет следующим геометрическим аксиомам.
1. На каждой прямой лежит n точек B.
2. Через каждую точку проходят n прямых.
3. Любые две прямые пересекаются в одной точке.
4. Через любые две точки проходит единственная прямая.
5. Существуют 4 точки неколлинеарные по три.
Тогда конечное множество P точек и множество L прямых образует конечную проективную плоскость.
Пример:
P = {1, 2, 3, 4, 5, 6, 7}.
L = {l1, l2, l3, l4, l5, l6, l7}
l1 = {1, 2, 3}, l2 = {3, 4, 5}, l3 = {1, 5, 6}, l4 = {1, 4, 7}, l5 = {2, 5, 7},
l6 = {3, 6, 7}, l7 = {2, 4, 6}.
Пример 1.
Александр, Питре, Дэйв, Роза, Люси часто ходят в столовую. Каждый раз, обедая там, они рассаживаются по-разному. Сколько дней сотрудники отдела смогут это сделать без повторения?
1)Пронумеруем стулья, на которых должен сесть каждый, и будем считать, что они рассаживаются поочередно:
№1 – Александр – есть возможность выбрать из 5 вариантов (стульев)
№2 – Питре – 4 варианта
№3- Дэйв – 3 варианта
№4- Роза – 2 варианта
№5 – Люси – 1 вариант
Используя правило умножения, получаем: 5х4х3х2х1=120
2)Используя понятие факториала: 5!=120
Пример 2.
В программном отделе лучше всех программирование на Java знают 5 кодеров: Вильям, Дак, Олов, Кэйт и Эприл. На конференцию по новым средствам программирования нужно отправить пару, состоящую из 1 юноши и 1 девушки. Сколькими способами директор может эту пару выбрать?
1) Обозначим имена кандидатов первыми заглавными буквами.
Получаем следующие пары:
В-К, В-Э, Д-К, Д-Э, О-К, О-А.
Ответ: 6 пар.
2) Юношей 3, из них 1 можно выбрать , девушек 2, из них можно 1 выбрать , используя правило умножения, получаем:
х = 6
Пример 3.
Лари на работе имеет 7 флеш-накопителей, а Роберт – 9. Сколькими способами они могут обменять 4 любых накопителя одного на 4 другого?
Вычислим, сколько четверок из 7 накопителей можно составить у Лари:
=35, число четверок у Роберта из 9 накопителей – = 126
По правилу умножения находим число обменов 35х126=4410
Пример 4.
Доступ к компьютеру системного администратора защищен паролем, состоящим из двух различных гласных букв русского алфавита, за которой следуют 3 различные цифры. Сколько вариантов придется перебрать хакеру получить доступ к его компьютеру?
В русском языке 9 гласных букв – а, е, е, и, о, у, э, ю, я. Выбрать из них 2 можно =36 способами. Из 10 цифр выбрать 3 можно =120 способами. Применяя правило умножения, получаем:
36х120=4320
Читайте также:
Рекомендуемые страницы:
©2015-2020 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-12-12
Нарушение авторских прав и Нарушение персональных данных
Поиск по сайту:
Источник
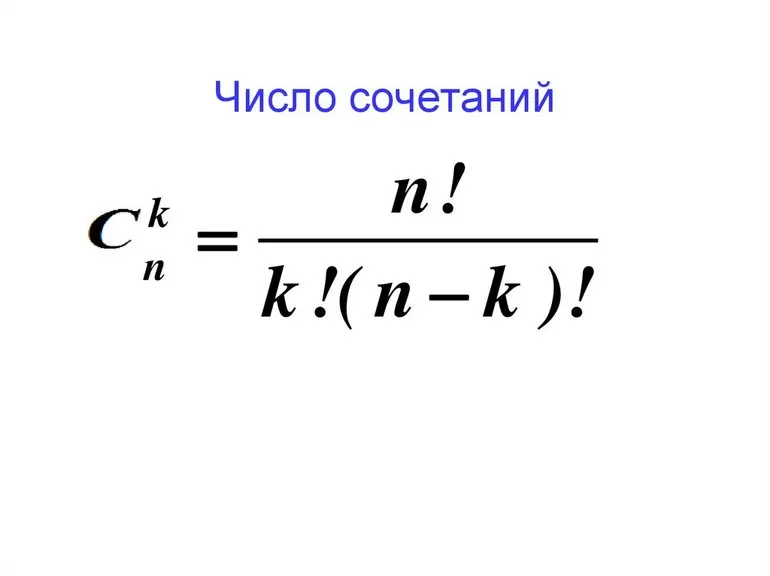
Краткое описание
Изучение математических правил не может обойти стороной число сочетаний из n по k. Формулы комбинаторики как науки активно используются во всех жизненных отраслях. Этот раздел включён в школьную программу старших классов и вступительные испытания многих вузов России. Удивительная комбинаторика лежит в основе прикладного искусства.

Это направление науки начало активно развиваться ещё шесть веков назад. Достоверно известно, что первые комбинаторные задачи присутствовали в трудах философов и талантливых математиков Средневековья. В те времена представители стремительно развивающегося научного мира всячески пытались найти актуальные методы решения поставленных задач, хотели определить основные правила и понятия, а также утвердить уникальные в своём роде формулы и математические уравнения для тех, кто ещё не знаком с этим научным направлением.
Актуальные формулы и нормы комбинаторики применяются в распространённой теории вероятностей, где специалисты могут быстро и качественно подсчитать процент случайных событий, чтобы в итоге получить закон реального распределения случайных величин. При правильном подходе можно углублённо изучать закономерности тех или иных событий, что очень важно для понимания статистических природных правил, которые неизбежно проявляются в окружающей природе и эксплуатируемой технике.
Ключевые нюансы
Используемое в математике число сочетаний с повторениями можно подробно изучить по книгам и специальным изданиям. Комбинаторика подробно описана в том разделе науки, который занимается многофункциональными операциями с множеством задействованных элементов.
Экспертами было доказано, что это направление затрагивает довольно большой математический пласт, в котором ученикам предлагается изучить, сколько в мире существует различных комбинаций, подчиняющихся определённым условиям. Основной задачей этой науки можно считать требование размещения различных объектов по специальным правилам и последующее нахождение точного количества способов таких расположений.

На просторах интернета можно встретить много различных учебников и другого познавательного материала по информатике/математике для школьников, а также специальные сборники уравнений и сложных примеров для студентов, где в доступном и максимально подробном виде объяснена довольно увлекательная и познавательная комбинаторика. В начальных классах задачи на эту тему решают на специальных кружках, а вот в гимназиях с углублённым изучением точных наук ей посвящают основные уроки. Многоуровневые задачи по комбинаторике включены в программу олимпиады.
Существует ряд базовых понятий, которые нужно усвоить учащимся:

- Если в конкретном примере f = n, то эти размещения называются исключительно перестановками.
- Размещение. В этом случае речь касается совершенно любого упорядоченного подмножества f из задействованных элементов множества n.
- Сочетания. В качестве основы может быть задействовано любое подмножество из элементов f, которые принадлежат изучаемому множеству, состоящему из n — различных элементов.
Необходимо отметить тот факт, что за основу может быть взят объект или целое явление, которое попадает в искомое множество. Перестановка затрагивает элементы, которые находятся в большом количестве и определённом порядке. Сочетание — своеобразные подмножества, пребывающие в произвольной форме. Размещение представляет собой упорядоченные подмножества в исходном множестве. Правильно посчитать нужный коэффициент можно при помощи многофункциональных онлайн-калькуляторов, которые обладают всеми необходимыми функциями.
Выборки и подсчёт суммы
Если предположить, что А = {a1… an} — множество из n элементов, то их совокупность будет называться выборкой объёма k из n. В этом случае действует ряд важных правил. Выборка может считаться правильно упорядоченной только в том случае, если итоговая последовательность следования всех задействованных элементов в ней была задана учеником заранее. Исключений не предусмотрено.
Различными выборками называются только те математические примеры, которые отличаются исключительно порядком следования элементов. Если отличия незначительные, тогда ученику предстоит работать с неупорядоченной комбинацией. В отдельных примерах могут допускаться или не должны допускаться повторения задействованных элементов.

Чаще всего перед учащимися возникает необходимость подсчёта точного числа вероятных выборок с определёнными математическими параметрами. Довольно часто для контроля над вероятными комбинаторными объектами используется два ключевых приёма — правила произведения и суммы. На каждый случай специалисты предусмотрели ряд важных правил, которые призваны обезопасить учащегося от различных ошибок.
Базовое требование математического произведения основано на том, что когда исследуемый объект А может быть выбран различными f способами, то итоговый выбор А и B в указанном ранее порядке может быть осуществлён f * n методами. Правило суммы отличается тем, что если ученик имеет несколько возможностей выбрать точку А, тогда поиск А или В можно будет осуществить по специальной системе f + n.
Действующее правило произведения
Именно это направление в комбинаторике является одним из базовых для решения поставленных задач. При тщательном выборе элемента А из n способов (В из m) правильным считается то утверждение, в соответствии с которым одновременно подобрать пару А и В можно n * m методами, что очень важно. На этот случай действует три основных утверждения:
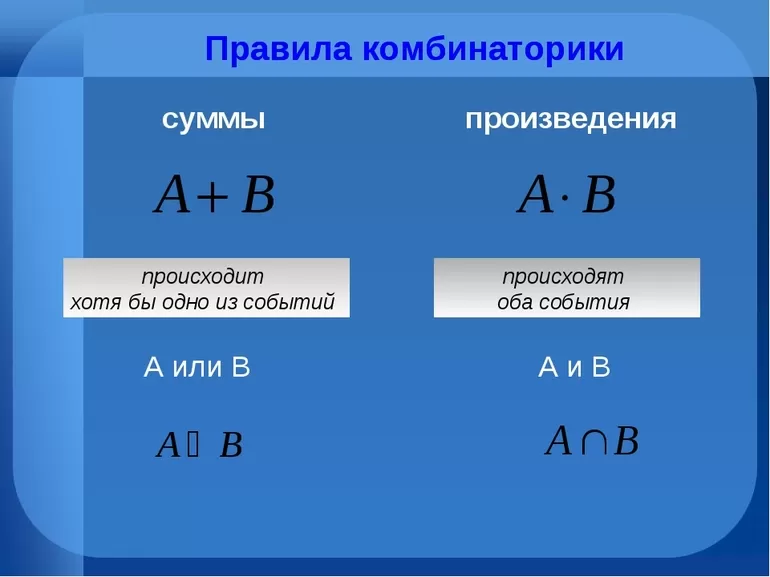
- Если ученику на каждом новом шаге известно количество доступных вариантов выбора, то для правильного определения суммарного количества способов необходимо все имеющиеся данные перемножить между собой.
- Когда есть возможность выбрать первый искомый элемент в задействованной комбинации любым a способом, а для второго примера можно применить вариант d, то общее число действий будет соответствовать формуле a * b. Это утверждение является наиболее распространённым.
- Если k способами можно безошибочно выбрать элемент x, а для Y подойдут имеющиеся m методы, тогда для пары x и y выполняется расчёт по формуле k * m. Данные можно записать в виде таблицы.
В эффективности описанных правил можно убедиться, благодаря некоторым примерам. По условиям задачи дано два ромба, три мяча, четыре гантели и пять кубов. Ученику нужно определить, сколькими способами можно будет вытянуть ромб, мяч, гантель и куб. Решение элементарное: 2*3*4*5= 120. Стоит отметить, что в этой задаче может быть задействован факториал, с помощью которого всегда можно вычислить более сложные варианты и решить трудные задачи.
По условиям следующего примера дано два мяча и пять скакалок. Задача состоит в том, чтобы определить, какова вероятность достать 1 скакалку и 1 мяч. Решение: 2*5=10.
Решение примеров комбинированного типа
Если ученик разобрался с основными свойствами сочетаний, то он также должен изучить уравнения всех доступных разновидностей задач с наиболее подходящими методами поиска правильных ответов. Эксперты рекомендуют потренироваться на более запутанных ситуациях, которые встречаются в повседневной жизни каждого человека. Основные категории задач:

- Специфический магический квадрат. По условиям необходимо отыскать фигуру, в которой итоговая сумма всех задействованных чисел в столбцах и рядах будет одинакова (основной тип — латинский квадрат). Для решения таких уравнений понадобятся рекуррентные соотношения. А вот для поиска правильного ответа придётся задействовать гораздо меньше элементов, которые применяются в востребованных формулах и правилах.
- Математические задачи про торговцев. Суть состоит в том, чтобы отыскать все реальные способы прохождения людей из стартового пункта A в точку B. В этом случае действует метод траектории. Для этой разновидности задач свойственно элементарное геометрическое проектирование возможных способов решения.
- Математические примеры с размещением. Классическая производственная задача (к примеру, используется в лоскутной методике) — отыскать все доступные способы разложения некоторого количества задействованных элементов в специальные ячейки, но только в чётком порядке. В этом случае действуют включения и исключения. Этот вариант применяется специалистами при доказательстве различных выражений.
Экспертами неоднократно было подтверждено, что комбинаторика является интересной и познавательной наукой, так как в наш век быстрой модернизации инновационных технологий постоянно будут нужны профессиональные специалисты, которые способны в полном объёме предоставить разнообразные решения для тех или иных практических задач.
Доступные размещения с повторениями и без них
Работа с различными математическими комбинациями подразумевает использование определённых правил, в противном случае избежать распространённых ошибок будет крайне сложно. Если имеющаяся l различных элементов может повториться m раз, оказавшись на имеющихся m местах, тогда при составлении вывода количество размещений с последующими повторениями вычисляется по определённой комбинаторной формуле — Am / l = lm. Именно под этим определением принято понимать чёткий набор компонентов m из множества l: A m/l = l * (l-1) * (l -2) *… * (l—m +1) = l!/(l—m)!.
Изучаемое число сочетаний без повторений сопряжено с некоторыми дополнительными нюансами. В этом случае в распоряжении учащегося имеется n разных математических элементов. Многих в такой ситуации интересует, сколько именно можно будет составить актуальных k расстановок.

Два базовых подхода считаются различными только при условии, если они отличаются друг от друга минимум одним элементом или состоят из аналогичных элементов, которые расположены в разном порядке. Каждый нюанс должен быть учтён, так как от этого зависит итоговый результат.
Изучаемые в этом случае расстановки указывают на право размещения без повторений, а вот их число обозначают как Ak / n (читается следующим образом: а из n по k). Первая буква является неотъемлемым элементом довольно известного французского слова Arrangement, которое означает «приведение в порядок». В такой ситуации популярность получила следующая формула: Ak / l = l (l -1) * (l -2)… (l — k +1). Специальные комбинации позволяют определить даже автомобильный региональный код.
Описанные правила и формулы позволяют решать довольно сложные и многоуровневые задачи. К примеру, из трёх предъявленных цифр нужно выбрать только две, чтобы в итоге получились разные двузначные числа. По условиям описанной задачи нужно определить, сколько вариантов существует в этом случае. Ответ: (4а) А2/3=3*2 = 6. Но также уместно следующее решение: А2/3 = 3!/(3−2)! = 3!/1! = 1*2*3/1 = 6. В этом случае каждый существующий элемент может быть расположен по несколько раз, что соответствует условиям задачи. Для этой ситуации уместна следующая формула: (5) Ak / l = lk.
Источник
