Какое основное свойство пропорции
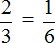
Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.
Что такое пропорция?
Пропорцией называют равенство двух отношений. Например, отношение ![]() равно отношению
равно отношению ![]()
![]()
Данная пропорция читается следующим образом:
Десять так относится к пяти, как два относится к одному
Дроби, из которых составлена пропорция, всегда равны. Например, если в пропорции ![]() выполнить деление в обеих дробях, то получится число 2 в обеих частях:
выполнить деление в обеих дробях, то получится число 2 в обеих частях:
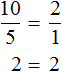
Предположим, что в классе 10 девочек и 5 мальчиков

Запишем отношение десяти девочек к пяти мальчикам:
10 : 5
Преобразуем данное отношение в дробь
![]()
Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки

Теперь рассмотрим другой класс в котором две девочки и один мальчик

Запишем отношение двух девочек к одному мальчику:
2 : 1
Преобразуем данное отношение в дробь:
![]()
Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:

Можно сделать вывод, что отношение ![]() пропорционально отношению
пропорционально отношению ![]() . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
. Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.
Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам

а также отношение 12 девочек к 2 мальчикам

Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что ![]() , поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
, поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
Поэтому отношение ![]() не пропорционально отношению
не пропорционально отношению ![]() .
.
![]()
Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция ![]() состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
Вторая рассмотренная нами пропорция была ![]() . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями
. Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями ![]() и
и ![]() знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения и равны между собой:
Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2
![]()
2 = 2
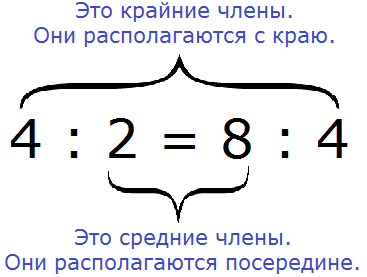
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.
В нашей пропорции ![]() крайние члены это 4 и 4, а средние члены это 2 и 8
крайние члены это 4 и 4, а средние члены это 2 и 8
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:
4 : 2 = 8 : 4
Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:
С помощью переменных пропорцию можно записать так:
![]()
Данное выражение можно прочесть следующим образом:
a так относится к b, как c относится к d
Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Основное свойство пропорции
Основное свойство пропорции выглядит следующим образом:
Произведение крайних членов пропорции равно произведению её средних членов.
Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.
Например, проверим правильно ли составлена пропорция ![]() . Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
. Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
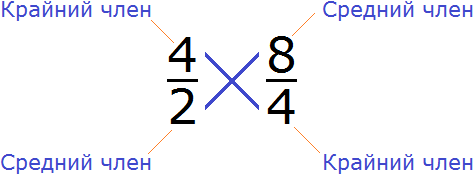
4 × 4 = 16 — произведение крайних членов пропорции равно 16.
2 × 8 = 16 — произведение средних членов пропорции так же равно 16.
4 × 4 = 2 × 8
16 = 16
4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция ![]() составлена правильно.
составлена правильно.
Пример 2. Проверить правильно ли составлена пропорция ![]()
Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:
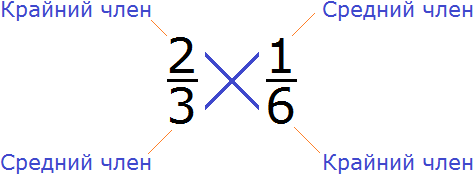
2 × 6 = 12 — произведение крайних членов пропорции равно 12
3 × 1 = 3 — произведение средних членов пропорции равно 3
2 × 6 ≠ 3 × 1
12 ≠ 3
2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция ![]() составлена неправильно.
составлена неправильно.
Поэтому в пропорции ![]() разумнее заменить знак равенства (=) на знак не равно (≠)
разумнее заменить знак равенства (=) на знак не равно (≠)
![]()
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Навигация по записям
Источник
Источник
Головач Александр Григорьевич
ГУО «Средняя школа №18 г. Бреста»
Тема: Пропорция. Основное свойство пропорции. (6 класс)
Тип урока: изучения и первичного закрепления новых знаний
Образовательная: познакомить учащихся с понятиями: пропорция и члены пропорции; научить чтению пропорции и составлению пропорций из отношений; познакомить учащихся с основным свойством пропорции и сформировать навык по определению верной пропорции.
Развивающая: активизировать познавательную деятельность учащихся; развивать память, логическое мышление;
Воспитательная: воспитывать уважение к труду, работе в коллективе.
Литература: Математика: учеб. пособие для 6 кл. общеобразоват. учреждений с рус. яз. обучения / Е. П. Кузнецова [и др.]; под ред. Л. Б. Шнепермана. – Минск: Нац. ин-т образования, 2010. — 320 с.: ил.
Оборудование: учебник, доска, мел, презентация, компьютер, проектор.
Ход урока:
Организационный момент (2 мин)
Проверка домашнего задания (3 мин)
Актуализация знаний (8 мин)
Изучение нового материала (12 мин)
Физкультминутка (2 мин)
Первичное закрепление (13 мин)
Задание на дом (1 мин)
Рефлексия. Подведение итого. (4 мин)
1. Организационный момент
Организую внимание учащихся. Предлагаю сесть. Отмечаю отсутствующих на уроке учеников.
Здороваются. Садятся.
2. Проверка домашнего задания
– Сегодня у нас на уроке новая тема «Пропорция. Основное свойство пропорции».
И цели нашего урока: познакомиться с определение «Пропорция»; из каких элементов состоит пропорция; изучить основное свойство пропорций.
Но перед тем, как приступить к изучению новой темы, давайте проверим домашнее задание.
3. Актуализация знаний
/*фронтальный опрос*/
– На прошлом уроке у нас была тема «Отношение чисел и величин».
1. Давайте вспомним, что же называется отношением?
2. А как называются сами эти числа или величины?
3. Скажите, что будет с отношением, если его члены умножить или разделить на одно и тоже число, отличное от нуля?
А теперь давайте вспомним, как читаются отношения и найдем их значение.
1.
2.
3.
4.
5.
6.
1. Частное двух чисел (или двух величин) называется отношением.
2. Эти числа или величины называются членами отношения.
3. Отношение не изменится, если его члены умножить или разделить на одно и тоже число, не равное нулю.
1. Отношение числа 25 к 5 равно 5.
2. Отношение числа 33 к 11 равно 3.
3. Отношение числа 6 к 14 равно .
4. Отношение числа 12 к 4 равно 3.
5. Отношение числа 30 к 70 равно
6. Отношение числа 55 к 11 равно 5.
4. Изучение нового материала
– Ребята скажите, под какими номерами у наших отношений получились одинаковые значения.
У нас получились записи равных отношений:
– Так вот равенство двух отношений называют пропорцией.
Пропорцию записывают:
или
Прочитать такую пропорцию можно по-разному:
– отношение a к b равно отношению c к d;
– a относится в b, как c относится к d;
– a, деленное на b, равно c, деленное на d.
Т.к. в записи числа a и d стоят с краю, то их принято называть крайними членами пропорции. Ну а т.к. числа b и c находятся в середине, то и называются они соответствующе – средними членами пропорции.
Эти названия сохраняются и тогда, когда пропорция записана в виде
.
Давайте вернемся к получившимся у нас пропорциям и назовем их крайние и средние члены.
А теперь немного посчитаем. Перемножьте в наших пропорциях крайние и средние члены
Какой вывод можно сделать?
, то
Верно. Это утверждение называется основным свойством пропорции.
Отношение 1 равно отношению 6.
Отношение 2 равно отношению 4.
Отношение 3 равно отношению 5.
Крайние 25 и 11, средние 5 и 55.
Крайние 33 и 4, средние 11 и 12.
Крайние 6 и 70, средние 14 и 30.
Произведение крайних членов пропорции равно произведению ее средних членов.
5. Физкультминутка
– Ну а теперь немного отдохнем. Проведем физкультминутку для глаз. Т.к. уже зима, то на экране будут появляться снежинки, а ваша задача внимательно следить за их движениями.
6. Первичное закрепление
– А теперь с новыми силами начнем выполнение заданий.
№ 5.27 (устно)
5.29 (1;3)
5.30 (1;3)
5.31 (1;3) (доп. 5.32)
№ 5.27
1) ;
2) ;
3) ;
4) .
№5.29 (1;3)
Составьте пропорцию, если m и n – ее крайние члены, а x и y – средние:
1) ;
3) ;
№ 5,30 (1;3)
Определите, является ли пропорцией равенство.
1)
3)
№ 5,31 (1;3)
1)
3)
№ 5.27
1) 5,1 относится к 3, как 34 относится к 20. Крайние члены: 5,1 и 20. Средние члены: 3 и 34.
2) 4,4 относится к 0,66, как 10 относится к 1,5. Крайние члены: 4,4 и 1,5. Средние члены: 0,66 и 10.
3) 4 относится к 25, как 16 относится к 100. Крайние члены: 4 и 100. Средние члены: 25 и 16.
1) 6 относится к 31, как 18 относится к 93. Крайние члены: 6 и 93. Средние члены: 31 и 18.
№5.29
1) или
3) или
№ 5,30 (1;3)
1) нет
3) нет
№ 5,31 (1;3)
1) да
3) да
7. Задание на дом
– Откройте дневники и запишите задание на дом: п.5.2 №5.29-5.31 (2;4)
8. Рефлексия. Подведение итого
Подведение итогов.
1. С каким новым определение Вы сегодня познакомились?
2. Что такое «Пропорция»?
3. Какие члены пропорции бывают?
4. Как звучит основное свойство пропорции?
Выставляю отметки за урок.
Рефлексия.
Предлагаю учащимся продолжить фразу:
“Сегодня на уроке я узнал…”,
“Было интересно…”,
“Было трудно…”,
“Меня удивило…”,
“Я хотел бы узнать…”,
“Сегодня на уроке я научился…”.
Ответы:
1. С определением «Пропорция».
2. Пропорция – это равенство двух отношений.
3. У пропорции бывают крайние и средние члены.
4. Произведение крайних членов пропорции равно произведению ее средних членов.
Источник
План урока
6.1АОтношения и пропорции
Школа: ГУ СОШ №39
Дата:
ФИО учителя: Ахметова Айнур Каиргельдиновна
Класс: 6 «Ж»
Участвовали:
Не участвовали:
Тема урока
Пропорция. Основное свойство пропорции
Цели обучения, достигаемые на этом уроке
6.1.2.3 – знать определение пропорции;
6.1.2.4 – распознавать и составлять пропорции;
6.5.2.2 – читать и записывать пропорции;
6.1.2.5 – знать и применять основное свойство пропорции.
Цель урока
– знать понятие пропорции, члены пропорции, основное свойство пропорции;
– применять основное свойство пропорции при решении уравнений.
Критерии оценивания
применяет понятие пропорции;
составляет пропорции по заданным условиям;
записывает пропорции;
находит неизвестные члены пропорции
применяет основное свойство пропорции.
Языковые задачи
Учащиеся могут:
– устно и письменно находить неизвестный член пропорции;- проверять полученные результаты, путем подстановки;
– аргументировать правильность выполнения заданий.
Предметная лексика и терминология:
– пропорция;
– основное свойство пропорции;
– крайние члены пропорции;
– средние члены пропорции;
– неизвестный член пропорции;
Полезные выражения для диалогов и письма:
Пропорцией называется…
Нахождение члена пропорции в математике называют действие…
Для определения верности пропорции …
Чтобы найти неизвестный член ….
Воспитание ценностей
«Национальное единство, мир и согласие в нашем обществе»
Взаимопомощь, сотрудничество – учащиеся должны уметь добывать самостоятельно информацию, анализировать ситуацию, работать в паре, организовывать свое время , анализировать проделанную работу и адекватно её оценивать
Межпредметная связь
физика
Предыдущие знания
Знает определение отношения
Ход урока
Запланированные этапы урока
Виды упражнений, запланированных на урок:
Ресурсы
Начало урока
Организационныймомент.
Приветствие;
Проверить готовность к уроку;
Отметить отсутствующих учащихся;
совместно определить тему и цели урока/ЦО в процессе повторения темы “Пропорция” и устного опроса;
определить «зону ближайшего развития» учащихся, ожидания к концу урока.
Мозговая атака
Найдите значение отношений
Сравните выражения
Что вы заметили?
Итак, вы нашли значение данных отношений и у вас получилось равенство выражений. Сегодня мы с вами пройдем тему «Пропорция».
Середина урока
Изучение нового материала.
«Общеклассная работа»
О. Верные равенство двух отношений называют пропорцией.
Общий вид пропорции:
a : b=c : dили
Чтение пропорции
так относится, как относится к.
отношение к равно отношению к
В пропорции a : b=c : d числа a иd называюткрайними членами пропорции, а числа b и c – средними членами пропорции..
средние
a : b = c : d
крайние
Дана пропорция:
1) Найдите произведение крайних членов
2) Найдите произведение средних членов
3) Что вы заметили?
Вывод: В пропорции произведение крайних членов ранво произведению средних членов.
Решение задач. Работа с классом.
№73. Запишите пропоцию
Дескрипторы:
– применяет определение пропорции;
– записывает выражения в виде пропорции.
№74.Составьте пропорции из отношений:
Дескрипторы:
-находит отношение чисел;
-составляет пропорцию.
Устная обратная связь
V. Парная работа.
Решите пропорцию:
х :15=4:5
21:x=6:4
8:9=x:27
6:7=9х:21
30:2x=9:3
Дескрипторы:
– определяет вид неизвестного члена пропорции;
-применяет правило нахождение среднего члена пропорции;
– находит неизвестный член пропорции.
ФО: Взаимнооценивание
VI.Индивидуальная разноуровневая работа.
Задание A
1. Запишите в виде пропорции утверждение:
1) отношение 9 к 3 равно отношению 15 к 5;
2) относится к , как относится к .
Дескрипторы:
– применяет определение пропорции;
– записывает выражения в виде пропорции.
2. Найдите неизвестный член пропорции:
1) х:18=2:3
2)6:х=3:7
3)
4)
Дескрипторы:
– определяет вид неизвестного члена пропорции;
-применяет правило нахождение крайнего (среднего) члена пропорции;
– находит неизвестный член пропорции.
ЗаданиеB
1.К трем данным числам подберите четвёртое, так, чтобы можно было составить пропорцию:
1) 11;7;66;
2) 162;27;36.
Дескрипторы:
– определяет четвёртый член пропорции;
– составляет пропорцию.
2. Используя основное свойство пропорции, составьте ее из множителей:
Дескрипторы:
-определяет члены пропорции;
-составляет пропорции.
ЗаданиеC
1. Отношение скорости первого всадника к скорости второго равно . Скорость первого 1,5 км/ч больше скорости второго.Найдите скорость первого всадника.
Дескрипторы:
-составляет пропорцию:
-находит неизвестный член пропорции.
Письменная обратная связь
https://bilimland.kz/ru/subject/matematika/6-klass/proporcziya-osnovnoe-svojstvo-proporczii
Учебник: Математика.Учебник для 6 класса -Т.А.Алдамуратова,К.С.Байшоланова, Е.С.Байшоланов-Алматы:Атамұра ,2018
https://uroky.kz/fo-matematika-6-klass-sbornik-zadanij-formativnogo-otsenivaniya
Конец урока
VII.Рефлексия. Стратегия «Телеграмма».Вам нужно кратко написать что вы уяснили с урока, и пишет пожелание соседу по парте.
-Что нового я узнал на уроке?
– Какое впечатление осталось у вас от урока?
Домашнее задание: Знать теорию о пропорции, №76, стр 35
Учебник
Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими?
Оценивание – как Вы планируете проверять уровень усвоения материала учащимися?
Охрана здоровья и соблюдение техники безопасности
Формы работы: Работа с классом, Индивидуальная разноуровневая работа, Парная работа;
По способу выполнения заданий(письменно, устно,
самостоятельная работа);
По оцениванию: взаимооценка, устная похвала учителя;
По степени трудности: от простого к сложному
ФО через выполнение индивидуального задания:
– Самооценивание стратегией «Телеграмма»
ФО учителем:
– Устная обратная связь;
– Взаимнооценивание;
– Письменная обратная связь.
При использовании ИКТ применять ТБ.
Источник
