Какое основное свойство дроби 5 класс
В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.
Основное свойство дроби, формулировка, доказательство и примеры
Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:
Определение 1
Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.
Представим основное свойство дроби в виде равенства. Для натуральных чисел a, b и mбудут справедливыми равенства:
a·mb·m=ab и a:mb:m=ab
Рассмотрим доказательство основного свойства дроби. Опираясь на свойства умножения натуральных чисел и свойства деления натуральных чисел, запишем равенства: (a · m) · b = (b · m) · a и (a : m) · b = (b : m) · a. Таким образом, дроби a·mb·m и ab, а также a:mb:m и ab являются равными по определению равенства дробей.
Разберем пример, который графически проиллюстрирует основное свойство дроби.
Пример 1
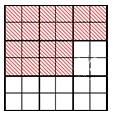
Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4·9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4·5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:

Окрашенная часть – это 59 исходной фигуры или 2036, что является тем же самым. Таким образом, дроби 59 и 2036 являются равными: 59=2036 или 2036=59.
Эти равенства, а также равенства 20 = 4·5, 36 = 4·9, 20:4 = 5 и 36:4 = 9 дают возможность сделать вывод, что 59=5·49·4 и 2036=20·436·4.
Чтобы закрепить теорию, разберем решение примера.
Пример 2
Задано, что числитель и знаменатель некоторой обыкновенной дроби умножили на 47, после чего эти числитель и знаменатель разделили на 3. Равна ли полученная в итоге этих действий дробь заданной?
Решение
Опираясь на основное свойство дроби, можно говорить о том, что умножение числителя и знаменателя заданной дроби на натуральное число 47 даст в результате дробь, равную исходной. То же самое мы можем утверждать, производя дальнейшее деление на 3. В конечном счете мы получим дробь, равную заданной.
Ответ: да, полученная в итоге дробь будет равна исходной.
Применение основного свойства дроби
Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.
Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.
Определение 2
Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.
Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.
Источник
МБОУ «Рыльская средняя общеобразовательная школа №4»
г.Рыльск Курская область
Открытый урок по теме
«Основное свойство дроби»,5 класс,
на районном семинаре-практикуме по теме
«Система работы учителей физико-математического цикла по созданию мотивационной среды для развития и стимулирования интереса школьников к занятиям математикой, физикой, астрономией, информатикой в условиях реализации ФГОС ООО и СОО».
Учитель: Семикина Татьяна Алексеевна
2018-2019 уч.год
Пояснительная записка
1.Предмет математика
2.Класс 5а
3.Тема и номер урока по теме «Основное свойство дроби»,1 урок
4.Тип урока урок открытия новых знаний
5.Базовый учебник Математика. Арифметика. Геометрия. 5класс/ Е.А. Бунимович, Г.В. Дорофеев, Л.В.Кузнецова, Л.О.Рослова. Изд. «Просвещение», 2017г./
6.Цели урока:
образовательная:
формирование умений выводить свойства на основе ранее полученных знаний, умения применять основное свойство дроби для преобразования дробей в равные им дроби;
развивающая:
развитие умения анализировать, сравнивать, обобщать, строить аналогии, делать выводы;
воспитательная:
развитие любознательности и интереса к предмету, ответственности за результаты своего труда, чувства взаимопомощи, поддержки, умения работать в коллективе.
Планируемые результаты:
Предметные:
знать основное свойство дроби, уметь применять свойство для преобразования дробей
Метапредметные:
самостоятельно ставить цели, выбирать и создавать алгоритм для решения учебных проблем, грамотно излагать свои мысли в письменной и устной речи
Личностные:
готовность и способность обучающихся к саморазвитию, бесконфликтно отстаивать свою точку зрения, осуществлять самоконтроль.
Методы работы:
проблемный, частично-поисковый, метод аналогий, наглядный, метод самостоятельной работы обучающихся.
Формы работы:
фронтальная, работа в группах, индивидуальная, коллективная.
Оборудование:
компьютер, проектор, раздаточный материал, электронная презентация
Сценарий урока «Основное свойство дроби»
Ход урока
1.Мотивизация к учебной деятельности
-Добрый день, ребята! Сегодня на уроке у нас присутствуют гости. Мне бы хотелось, чтобы им было уютно, комфортно и самое главное интересно. Постараемся? Итак… Начинаем мы урок!
Человек подобен дроби, числитель есть то, что он есть, а знаменатель то, что он о себе думает. Чем больше знаменатель, тем меньше дробь. ( Л. Н. Толстой)
Как вы понимаете эти слова? (Ответы вызывают затруднения)
2.Актуализация знаний и фиксирование индивидуального затруднения в пробном действии
-Ребята, нужны ли в жизни человеку математические знания?
-А математика может обойтись без дробей? Почему? (Ответы детей)
-Кто из вас прошел тур олимпиады по математике на сайте учи.ру?
Были задачи на дроби? Как вы справились с ними?
-В семье моих друзей пятиклассник Саша проходил основной тур олимпиады по математике на сайте учи.ру. Он не смог решить задачу:
«В семье трое детей. Сладости родители решили разделить таким образом:
Маше—10/50 сладостей,
Марине—–5/25 сладостей,
а Мише—2/10 сладостей.
Миша немного обиделся.
Каким образом дети должны разделить угощения между собой?»
(Ответы детей)
-Вот видите, вам не хватает еще знаний, чтобы правильно ответить на этот вопрос, поэтому нам придется повторить изученный материал по теме «Дроби» и помочь Саше решить задачу.
3.Этап выявления места и причины затруднения
На экране числа:
а) 2/5, 1/4, 20/40, 5/3, 15/60, 44/25, 1/2
1.Прочитайте дроби (все вместе)
2. Назовите правильные и неправильные дроби. Дайте им определение.
3.Что показывает числитель(знаменатель) дроби?
4.Нет ли среди дробей равных? Почему вы решили, что они равные? Сравните записи этих чисел.
-Откройте тетради, запишите число, классная работа. Запишите в тетрадь равные дроби. Попробуйте дать определение равных дробей.
б) Работа парами.
1)- Перед вами лежат геометрические фигуры. Возьмите квадрат, сверните его, чтобы получилось:
1 вариант : 1/2 квадрата
2 вариант : 2/4 квадрата
Отрежьте 1/2 и 2/4 , сравнить наложением, сделайте вывод (получили равные фигуры)
2)1вариант : 3/9 прямоугольника
2 вариант : 1/3прямоугольника
Отрежьте 3/9 и 1/3 , сравнить наложением, сделайте вывод (получили равные фигуры)
-Запишите результаты своей работы в тетрадях(один человек —на доске) .
1/ 2=2/4; 3/9 =1/3
-Какие же дроби получили? (равные)
Какие же дроби называются равными?
Давайте сформулируем определение равных дробей.(Две равные дроби являются различными записями одного и того же числа)
-Отметьте усвоение материала на полях тетради («+»-усвоил(а), «+-»-допустил(а) ошибку, «?!»-нужно разобраться)
-Итак, дроби равны. Но мы не можем всегда заштриховывать, вырезать и сравнивать дроби наложением.
4.Этап построения проекта выхода из создавшейся ситуации
Проблемный вопрос.
– Как же одну дробь получить из другой? (дети отвечают).
Это свойство очень важное в математике, поэтому его называют «основным».
Можно ли умножать числитель и знаменатель на 0?(нельзя)
Основное свойство дроби можно записать и на математическом языке( слайд)
Вы, ребята, сделали открытие!!!
Подскажите мне, пожалуйста, какая же тема нашего урока? Какие цели и задачи нам необходимо решить на уроке?
5.Реализация построенного проекта. Первичное закрепление новых знаний
а)-А где мы можем проверить правильно ли сделали вывод?
Верно, в учебнике. Давайте сравним наше определение с определением в учебнике. Найдите его. Стр.140-141,п.30. (Читают правило, запоминают, стараются рассказать)
Выполнение заданий
№491,492,493.
-У кого есть вопросы? Если нет, тогда попробуем выполнить задание в «парах» и посмотрим, что у нас получится.( проектор)
№1.

№2. Знали ли вы раньше, что 1/4 и 15/60 часа – это одно и то же время? Какое свойство помогает вам это понять?
3.Решение задачи:
Мама дала Пете 3/9 , а Оле 9/16 плитки шоколада. Не
возникнет ли у детей спор?
4.Найди ошибку в заданиях:
8/10=4/5; 24/32=3/4; 10/20=1/2; 7/21=1/7
-Отметьте усвоение материала на полях тетради («+»-усвоил(а), «+-»-допустил(а) ошибку, «?!»-нужно разобраться)
б)Проверь свою память(проектор)
-Сейчас Вы увидите дроби, которые «исчезнут» через 15 секунд.
Попробуйте их запомнить, а затем записать в тетрадь. Если Вы запомните хотя 5 дробей, то у вас хорошая память.
Готовы к проверке?
Дети записывают по памяти дроби в тетрадь. Затем проверяют
Кто заметил равные дроби? Запишите их.(5/10=1/2)
-Отметьте усвоение материала на полях тетради («+»-усвоил(а), «+-»-допустил(а) ошибку, «?!»-нужно разобраться)
4.Самостоятельная работа по эталону
Выполнить задание самостоятельно по вариантам (верхняя строка-1вариант, 2 строка-2 вариант) с последующей взаимопроверкой.
10/20, 4/5, ¼, 11/14, 13/14, 1/2, 8/10—-1вариант
14/20, 7/10, 20/40, 2/3, 8/3, 2/5, 1/2—2 вариант
Найти равные дроби.
-Отметьте усвоение материала на полях тетради («+»-усвоил(а), «+-»-допустил(а) ошибку, «?!»-нужно разобраться)
Теперь мы можем помочь Саше решить задачу:
В семье трое детей. Сладости родители решили разделить таким образом:
Маше—10/55 сладостей,
Марине—–5/25 сладостей,
а Мише—2/10 сладостей.
Миша немного обиделся.
Каким образом разделить угощения между детьми?(дроби равные)
-Запишите дроби.
10/55=1/5; 5/25=1/5; 2/10=1/5
10/55=5/25=2/10=1/5
Все ли угощения съедят дети? Кого они угостят?
-Молодцы,ребята, мы смогли ответить на вопрос задачи и помочь Саше.
-Отметьте усвоение материала на полях тетради («+»-усвоил(а), «+-»-допустил(а) ошибку, «?!»-нужно разобраться)
-Вы немного устали.Проведем физминутку. Я называю числа: если целое число—руки в стороны,если правильная дробь-руки вверх,если неправильная дробь-хлопаем в ладоши.
5.Включение новых знаний в систему знаний
а)Расположите в порядке возрастания дроби
2/3,1/4,7/12, 1/6.(Задания ОГЭ)
а)Попробуйте выполнить задание
4/10+3/10=?
2) 1/3+3/6=?
-Отметьте усвоение материала на полях тетради («+»-усвоил(а), «+-»-допустил(а) ошибку, «?!»-нужно разобраться)
6.Подведение итогов.
Учитель предлагает вспомнить, чем занимались на уроке, как установили основное свойство дроби? Сформулировать основное свойство дроби, определение равных дробей.
– Удалось ли нам решить поставленные перед нами задачи?
-Посмотрите усвоение вами учебного материала в оценочных листах(поля тетради).
-Как же вы понимаете слова?
Человек подобен дроби, числитель есть то, что он есть, а знаменатель то, что он о себе думает. Чем больше знаменатель, тем меньше дробь. ( Л. Н. Толстой)
Домашнее задание
Учитель комментирует домашнее задание. П.30.У.,№493,499,З.№280,281.
По желанию подготовить сообщение о том, как возникли дроби.
Рефлексия.
-Оценим свою работу. Покажи свое настроение по результатам работы на уроке.
Усвоили материал-поднять две руки.
Были трудности-поднять одну руку.
Спасибо за урок
Источник
Теория
| 1. | Сокращение и расширение дробей |
Задания
| 1. | Дробь с меньшим знаменателем Сложность: | 1 |
| 2. | Дробь с меньшим числителем Сложность: | 1 |
| 3. | Расширение дроби, известный знаменатель Сложность: | 1 |
| 4. | Обыкновенная дробь, циферблат Сложность: | 2 |
| 5. | Какую часть часа составляют минуты Сложность: | 2 |
| 6. | Запись обыкновенной дроби, если дано целое и часть Сложность: | 2 |
| 7. | Основное свойство дроби Сложность: | 3 |
| 8. | Дробь с данным знаменателем Сложность: | 3 |
| 9. | Приведение дробей к общему знаменателю (две дроби) Сложность: | 2 |
| 10. | Количество долей в дроби Сложность: | 3 |
| 11. | Сокращение дроби Сложность: | 2 |
| 12. | Распределительный закон, сокращение дроби Сложность: | 3 |
Тесты
| 1. | Тренировка по теме Основное свойство дроби Сложность: среднее | 6 |
Методические материалы
| 1. | Технологическая карта |
Источник
Самоанализ открытого урока математики в 5 классе
Тема урока: “Основное свойство дроби”.
Специфика и уникальность данного урока заключается в использовании новых педагогических технологий (обучающих структур) по Сингапурской методике.
Тип урока: урок закрепления изученного материала. Раздел «Обыкновенные дроби». Заключительный урок по теме «Основное свойство дроби».
Цель: закрепить умение применять основное свойство дроби при решении задач.
Задачи:
Обучающие: – повторить основное свойство дроби;
– развивать умение подводить дроби к заданному знаменателю, сокращать дроби;
– повторить основные правила сравнения дробей.
Воспитательные: – добросовестное отношение к труду: ответственное выполнение заданий, дисциплинированность, собранность;
– определить правила работы в паре.
Развивающие: – развитие мышления: умения анализировать, сравнивать определять и объяснять понятия, ставить и разрешать проблемы;
– развитие умения управлять своими двигательными действиями.
Урок состоял из следующих этапов: организационный момент, проверка домашнего задания, актуализация знаний, решение задач, подведение итогов.
Для реализации цели и задач урока были использованы следующие образовательные структуры:
- Сигнал тишины,
- Тим Чир,
- Тэйк оф-тач даун,
- Куиз-куиз трейд,
- Сималтиниус релли тейбл,
- РАФТ,
- Билетик на выход.
В организационном моменте я использовала структуру Тим Чир – это короткое и веселое упражнение для поднятия духа аудитории, поощрения или выражения благодарности.
На этапе актуализации знаний для проверки правильности выполнения заданий была использована структура Тэйк оф-тач даун. Это обучающая структура для получения информации о классе, т.е. таким образом я узнала, насколько класс справился с данным заданием.
Для двигательной разминки я выбрала структуру Куиз-Куиз-Трейд – обучающая структура, в которой учащиеся проверяют и обучают друг друга по пройденному материалу, используя карточки с вопросами и ответами по теме. Здесь была проведена работа по повторению основных правил сравнения дробей.
На этапе решения задач была применена структура РАФТ (Роль-Аудитория-Форма-Тема) – более структурированный вариант организации работы. Ученикам было предложено задание составить памятку для учащихся 5 классов по вопросу «Приведение дроби к заданному знаменателю», т.к. в учебном пособии Зубаревой и Мордковича «Математика 5 класс» нет словесной формулировки данного правила. С помощью РАФТа обучающиеся разработали алгоритм выполнения действий для приведения дроби к новому знаменателю.
Также использовалась структура Сималтиниус релли тэйбл – обучающая структура, в которой ученики одновременно выполняют письменную работу на отдельных листочках (тетрадях) и по окончанию одновременно передают друг другу. Взаимопроверка – по шаблону на доске. Такая форма проверки значительно активизирует деятельность, повышает интерес к предмету, активизирует работу не только сильных, но и слабых учеников.
Также на протяжении всего урока прослеживались 4 принципа, необходимых для успешной работы в команде (PIES).
Домашнее задание дано дифференцированное, 1 обязательное задание и 1 творческое, по выбору.
Исходя из всего выше сказанного, цель урока была достигнута, задачи выполнены. Двигательная активность высокая, урок закончился вовремя, дозировка соблюдена. На данном уроке были использованы все возможности для обучения, воспитания и развития учащихся.
Считаю, что применение структуры Сингапурской системы обучения положительно сказывается на работе учащихся при проведении уроков. Она творчески развивает личность каждого ученика, заставляет его думать, проявляться, позволяет изменять видение материала, повышает его эмоциональный уровень, заставляет работать каждого ученика, независимо от его способностей.
Источник
