Какое общее свойство у квадрата и треугольника
В статье дается определение, основные свойства и формулы для следующих геометрических фигур:
Четырехугольник (общее для всех четырехугольников)
Квадрат
Прямоугольник
Параллелограмм
Ромб
Трапеция
Треугольник
Окружность
Четырёхугольник
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.
Основные свойства:
- Сумма углов четырёхугольника равна 360°
- Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
- Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
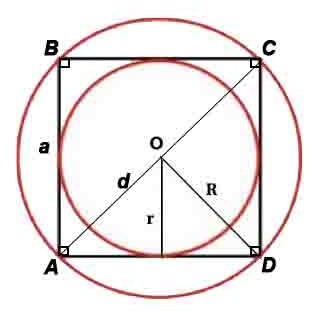
Квадрат
Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Основные формулы:
Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a2или S=d2/2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2
где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.
Свойства:
- Все стороны равны, все углы равны и составляют 90°;
- Диагонали квадрата равны и перпендикулярны;
- У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
- Квадрат является одновременно частным случаем ромба и прямоугольника.
Прямоугольник
Прямоугольник — четырехугольник, у которого все углы прямые.
Основные формулы:
Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a2+b2)/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a2+b2)/2 (теорема Пифагора)
где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a2+b2) – корень квадратный из (a2+b2).
Свойства:
- Диагонали прямоугольника равны и делятся точкой пересечения пополам.
- Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.
Параллелограмм
Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Определения:
Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.
Основные формулы:
Стороны и диагональ связаны соотношением: (d1)2+(d2)2=(a2+b2)*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
Площадь по двум сторонам и углу между ними: S=a*b*sin α
Площадь по двум диагоналям и углу между ними: S=(d1*d2)/2*sin γ
где a, b — длины сторон, d1, d2 –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).
Свойства:
- У параллелограмма противоположные стороны равны и противоположные углы равны.
- Сумма любых двух соседних углов параллелограмма равна 180°.
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит параллелограмм на два равных треугольника.
- Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
- Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Основные формулы:
Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d1*d2)/2
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a2 · sin α
Радиус окружности, вписанной в ромб: r=h/2 или r =(d1*d2)/4a
где a — длина стороны, d1, d2 –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба
Свойства:
- Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
- В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d1*d2/4a.
Трапеция
Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.
Определения:
- Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
- Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
- Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
- Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
- Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
- Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.
Основные формулы:
Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2
где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d1, d2 –диагонали,
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне
Свойства:
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
Треугольник
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
Определения:
- Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
- Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
- Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
- Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
- Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
- Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
- Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
- Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
Основные формулы:
Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь по сторонам и углу между ними: S=(a*b)/2* sin γ
Площадь по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
Площадь по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c2=a2+b2 (Теорема Пифагора)
где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
d1, d2 –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности
Свойства:
- В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
- Сумма углов треугольника равна 180°:
- Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| <c<a+b
- Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
- Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
- Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
- В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
- Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2=a2+b2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.
Окружность
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.
Определения:
- Радиус — отрезок, который соединяет центр окружности с любой её точкой.
- Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
- Диаметр — хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
- Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
- Секущая — прямая, которая пересекает окружность в двух различных точках.
Основные формулы:
Длина окружности: L = 2πR
Площадь круга: S = π*r2 или S = π*d2/4
где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.
Источник
загрузка…
Конспект интегрированного урока
по математике и конструированию
в старшей группе
/с элементами развивающего обучения/
Тема: «Треугольник и квадрат. Сравнение геометрических фигур»
Цель: Знать свойства треугольника и квадрата. Уметь сравнивать их по основным признакам. Уметь преобразовывать квадрат в треугольник и конструировать поделку оригами. Развивать наблюдательность, внимание и умение применять полученные знания при решении учебных задач. Развивать умение ориентироваться в пространстве. Уметь получать удовольствие от полученных результатов каждым ребенком на уровне его развития. Уметь общаться со сверстниками в парах. Развивать навыки коммуникативности в командной работе.
Ход урока
Организационный момент
– Чтобы нам начать занятие, нам нужно выполнить небольшое задание.
Детям раздаются карточки с зашифрованной геометрической фигурой.
I Ситуация успеха
1 Дидактическая игра «Зашифрованная фигура»
– Вспомним, как правильно нужно определять свою фигуру. Смотрим слева направо. Что определяем сначала? /Какая геометрическая фигура/. Затем? /Величину/. И потом? /Цвет геометрической фигуры/.
– Ребята, когда вы расшифруете и найдете свою геометрическую фигуру, определите свой стол. Сядьте за тот стол, на котором изображена ваша геометрическая фигура.
2 Рефлексия.
Предлагаю положить карточки перед собой.
Работа в парах. Проверка друг у друга выполненного задания: правильно ли дети определили свою геометрическую фигуру и нашли свой стол.
Назначаю лидеров команд.
3 Определение темы урока.
– Ребята, как называется ваша геометрическая фигура? /У одной команды это треугольник, у другой – квадрат/.
– Как вы думаете, о чем мы сегодня будем говорить на уроке?
– Верно, мы сегодня вспомним все, что мы знаем о треугольнике и квадрате, узнаем чем они похожи и в чем их различие.
II Основная часть
1 Дидактическая игра «Узнай, кто это»
На доске висит иллюстрация с изображением забавных животных, расположенных в ряд.
– К нам в гости должен прийти один из этих забавных животных. Нам нужно определить кто это по следующей подсказке: он стоит впереди бельчонка, но позади щенка.
Дети определяют, что это Ёжик. Вносится игрушка ёжика.
– Ёжик привел нас на полянку, на которой стоят два веселеньких домика /плоскостных/.
– Ребята, вы хотите узнать, кто в этих домиках живет? Тогда нам нужно выполнить одно задание.
2 Дидактическая игра «Пропущенная цифра»
Лидеры раздают каждому ребенку по одной карточке, по которой определяется пропущенная цифра. Каждый ребенок выкладывает соответствующее количество кружочков. Индивидуальная работа.
Рефлексия.
Проверка в парах выполненного задания.
– С заданием мы справились? Тогда наш гость ёжик, наконец, покажет нам, кто живет в этих домиках.
В домиках открываются окошки и дети видят в одном домике квадрат, в другом треугольник.
3 Закрепление знаний о треугольнике и квадрате.
– Давайте вспомним все, что мы знаем об этих геометрических фигурах.
Кластер
Работа в команде.
У каждой команды есть таблица, которую нужно заполнить: вставить в окошечки цифры, обозначающие количество сторон, углов и вершин, которые ранее дети обозначали модулями:
Стороны углы вершины
Рефлексия.
Таблицы вывешиваются на доске. Лидер определяет, кто из команды будет защищать свой проект. Дети от каждой команды выходят к доске и рассказывают по своей таблице о геометрической фигуре:
– У треугольника 3 стороны, 3 угла и 3 вершины.
– У квадрата 4 стороны, 4 угла, 4 вершины.
Валеопауза.
– А теперь отдохнем и повеселим друзей.
У треугольника есть брат –
Замечательный квадрат.
Братья делают зарядку,
А потом играют в прятки,
Сладкий чай из чашек пьют,
Очень весело живут.
Треугольник и квадрат –
Старший брат
И младший брат.
4 Конфликтная ситуация
– Ёжик хочет рассказать вам одну историю, которая произошла с этими геометрическими фигурами. Хотите послушать?
Жили-были два друга: треугольник и квадрат. Жили они дружно. Ходили они друг к другу в гости, чай пили, сказки рассказывали. Но вот однажды квадрат сказал треугольнику: «Мы с тобой словно братья, мы ведь так похожи! «Нет,- говорит треугольник, – мы совершенно разные, совсем не похожи!» Стали они спорить и окончательно поссорились. И дружбе их пришел конец. Не стали треугольник и квадрат ходить друг к другу в гости, чай пить, сказки рассказывать.
– Ребята, давайте поможем друзьям. Посоветуйтесь в командах и решите этот спор: чем похожи и чем не похожи друзья.
Итог
– Друзья похожи тем, что у них есть стороны, есть углы и есть вершины. Но не похожи они тем, что количество сторон, углов и вершин у них разное.
Рефлексия
– Ребята, мы смогли решить спор друзей? Мы молодцы?
III Заключительная часть.
1 Конструирование оригами «Тюльпан»
– Чтобы окончательно помирить друзей, давайте приготовим им сюрприз: сделаем поделку оригами. Будьте внимательны и точно выполняйте мои инструкции, и тогда мы увидим, что у нас получится.
– Возьмите цветной лист бумаги. Какой он геометрической формы? /Это квадрат./
– Докажите, что это квадрат. /У этой фигуры 4 стороны, 4 угла и 4 вершины. Все стороны равны, значит, это квадрат./
– Вы меня убедили. Превратите свой квадрат в треугольник.
Перегибаем квадрат по диагонали пополам, совмещая углы и стороны.
– Прогладьте пальчиком сгиб. Положите перед собой так, как у меня.
Треугольник располагаем длинной стороной вниз.
– Что за фигура у нас получилась? /Треугольник, потому что у него 3 стороны, 3 угла, 3 вершины./
– Поставьте указательный пальчик левой руки на середину длинной стороны треугольника.
– Поднимите острый уголок вверх и немного в сторону, прогладьте пальчиком сгиб.
– Теперь поднимите второй острый уголок также вверх и немного в сторону, прогладьте.
– Что у нас получилось? /Тюльпаны!/
– Давайте соберем их в красивый букет и подарим нашим друзьям.
Дети приклеивают тюльпаны к готовым цветоножкам на панно с вазой. И дарят свою работу квадрату и треугольнику. Благодарят ёжика за интересную историю.
Рефлексия
– Ребята, как вы думаете, смогли бы мы сделать такие замечательные тюльпаны, если бы квадрат и треугольник перестали дружить?
– А что нам сегодня помогло при работе на уроке? /Дружба, взаимопомощь, поддержка товарища, аккуратность, внимательность./
Итог урока
– Я вас благодарю за урок, за то, что вы смогли помирить друзей. Вы все молодцы. Мне очень понравилось как вы работали. Урок окончен.
Щербакова В.П.
Воспитатель д/с № 22
г. Риддер
Рахмет ретінде астында тұрған жарнамалардың біреуін басуды сұраймын!
Источник
Цели:
- актуализировать знания о многообразии свойств
объектов, их категорий; - сформировать представление об общих и
отличительных свойствах объектов; - познакомить со спецификой общих и
отличительных свойств.
Педагогические задачи урока:
- раскрыть смысл понятия “общие свойства” на
основе анализа примеров; - раскрыть смысл понятия “отличительные
свойства” на основе анализа примеров; - закрепить умение производить характеристику
объекта; - развивать основные мыслительные операции
анализа, синтеза, обобщения, сравнения на
предметном, образном, понятийном материале; - развивать информационную культуру посредством
формирования общих способов решения
информационных задач.
Ключевые понятия:
- общие свойства
- отличительные свойства
Вспомогательные (дополнительны) понятия:
- группы объектов
- характеристика объектов
Форма урока – диалог с опорой на знания и
опыт учащихся, фронтальная работа (решение
информационных задач в рабочей тетради)
Тип урока – урок объяснения
Стратегия – опережающая, развивающая.
Обеспечение урока:
- учебник;
- рабочая тетрадь № 2;
- демонстрационный ПК и мультимедиа-проектор;
- презентация к уроку;
- карточки с изображением предметов.
Полезные правила для урока:
- Улыбнись себе и другим.
- Научись любить.
- Не заносись.
- Радуйся успеху.
- Береги своё здоровье.
- Не бойся ошибок, помни – в классе тебе всегда
помогут. (Слайд 1, см. Приложение 1).
План урока
- Организационный момент (1–2 мин)
- Повторение материала предыдущей темы в виде
игры (3 мин) - Обобщение сведений, известных учащимся, с
выходом на новый материал (6 мин) - Физкультминутка (1–2 мин)
- Продолжение работы над темой урока с
закреплением полученных знаний (3 мин) - Психологическая пауза (1 мин)
- Выполнение заданий в рабочей тетради (12 мин)
- Обобщение и закрепление. Подведение итогов (3
мин) - Комментарии к домашнему заданию (1 мин)
- Рефлексия (2 мин)
Ход урока
1. Организационный момент
– Добрый день, ребята! Добрый день. уважаемые
гости. Я хочу, чтобы у всех сегодня было доброе
настроение. Давайте улыбнёмся друг другу. И будем
по-доброму относиться друг к другу, по-доброму
работать, мыслить. Не зря народная мудрость
гласит:
Слайд 2
“Где доброта, там красота”
– Пусть это станет девизом нашего урока!
2. Повторение материала предыдущей темы
а) – Предлагаю проверить домашнее задание и
провести игру-разминку.
Правила игры следующие:
К доске выходят четыре ученика и получают
карточки с названием предметов. Никто никому не
говорит, какая карточка ему досталась. Я называю
свойство, а ученики поднимают руки, если их
объект этим свойством обладает. Затем мы должны
будем отгадать, какой объект изображён на
карточке у каждого из них. Договорились?
Яблоко
Арбуз
Машина
Самолёт
Свойства объектов:
круглый, может летать, съедобный, вкусный, сочный,
гудит, перевозит людей, большой.
– Кто догадался, какой предмет у каждого
ученика?
– Что помогло вам в этом (свойства предмета)
Слайд 3
b) – Скажите:
- Какими свойствами обладает книга?
- Какими свойствами могут отличаться друг от
друга книги? - Назовите известные вам свойства
– человека;
– собаки;
– кошки.
Назовите несколько объектов, которые обладают
свойством “круглый”, “прямоугольный”,
“бумажный”, “стеклянный”.
Назовите какое-нибудь свойство объекта с именем
“телевизор”, “магнитофон”, “компьютер”
3. Обобщение сведений, известных учащимся, с
выходом на новый материал
– Как вы поняли из предыдущих уроков, у каждого
объекта множество свойств. Но если мы будем
сравнивать объекты между собой, то увидим, что
свойства объекта бывают общими и отличительными.
Этой теме и посвящён наш сегодняшний урок.
Слайд 4
– Исходя из темы как думаете, какие
информационные задачи мы сегодня будем решать, т.
е. что нам предстоит делать?
Слайд 5
– Посмотрите на экран и скажите, чем похожи
самолёт и пароход? (Это средства передвижения, и
то, и другое транспорт).
– Можно сказать, что это общее свойство данных
объектов? (можно)
– А теперь скажите, чем они различаются? (Самолёт
воздушный транспорт, а пароход – водный)
– Правильно, это их отличительные свойства:
плавать по воде и летать по воздуху.
– Теперь давай те рассмотрим сразу несколько
объектов – например, учеников нашего класса.
Давайте все встанем. Какое общее свойство у всех? (Быть
учениками, быть детьми).
– Теперь выделим из данной группы объекты с
отличительным свойством “быть девочкой”.
Девочки сядьте. Для девочек это свойство общее
или отличительное? (Общее)
– Теперь выделим из группы девочек объекты, с
отличительным свойством “быть выше всех”. Пусть
такие девочки встанут. Это их отличительное
свойство.
– Садимся на места. Давайте обсудим то, что мы
наблюдали. Как видим, одно и то же свойство “быть
девочкой” может быть и общим, и отличительным.
Оно отличительное, когда группа девочек входит в
более широкую группу объектов – в класс, в
котором кроме них есть ещё и мальчики.
– Рассмотрим ещё один пример. Внимание на экран
Слайд 6
– Как назвать одним понятием изображённые на
слайде объекты?(геометрические фигуры)
– Решим такую задачу: выделим из представленных
на этом рисунке геометрических фигур такие,
которые имеют свойства “иметь углы”
– Это отличительное свойство выделенных фигур
от остальных.
– Рассмотрим получившуюся новую группу:
Слайд 7
– Заметим, что теперь свойство “иметь углы”
уже не отличительное, а общее, поскольку все
фигуры этой группы имеют углы.
– Теперь выделим из данной группы объекты с
отличительным свойством “иметь ровно три угла”.
Такой объект в этой группе один – треугольник. Слайд
8
– Проанализируем проделанную работу.
– Мы видим, что одно и то же свойство может быть
либо общим для группы объектов, либо
отличительным.
– Так свойство “иметь углы” является для
квадратов, прямоугольников и треугольников
общим. Это же свойство будет отличительным для
квадратов, прямоугольников и треугольников, если
в состав группы ввести круги и овалы.
4. Физкультминутка
5. Продолжение работы над темой урока с
закреплением полученных знаний
– В нашей работе встретились такие ключевые
понятия как
Слайд 9
- общие свойства
- отличительные свойства
– Кто может дать определение этим понятиям? (ответы
детей)
– А теперь давайте обратимся к учебнику и
познакомимся с определением, которое даёт этим
понятием Н.В. Матвеева
Работа с учебником (с. 95)
Слайд 10
– Итак свойства объектов бывают общие и
отличительные.
Слайд 11
– Назовите хотя бы одно общее свойство у таких
разных объектов, как луна и мяч.
– Назовите отличительные свойства данных
объектов.
– А теперь посмотрим как эти знания могут помочь
нам на других уроках, например на уроке русского
языка.
Слайд 12
– Объектами выступают слова: картина,
квартира, корова
– Найдите общие и отличительные свойства.
(Общие свойства: все словарные
слова,
все имена существительные,
все трёхсложные,
все начинаются с один. звука
все имеют окончание а
Отличаются безударными гласными а и о)
Слайд 13
Литературное чтение: “Курочка Ряба”,
“Теремок”, “Золотая рыбка”
(Общие свойства – одна жанровая
принадлежность – сказки
Отличия: по классификации)
– Попробуйте сами привести подобные задания
например с числами (заготовка 3 12 15 18) Слайд 14
6. Психологическая пауза
Слайд 15
Ох, как хочется трудиться!
Делать всё охота.
Чтоб трудом своим гордиться,
Пусть кипит работа.Я и бодр, и силён,
Всю работу сделаю.
Свою волю покажу.
Слово для себя сдержу.
7. Выполнение заданий в рабочей тетради
с. 26–27, с. 30–31 (табличка)
8. Обобщение и закрепление. Подведение итогов
– А теперь давайте снова поиграем.
– Угадайте животное по выделенным признакам (Слайд
16)
- Бегает, прыгает, длинные уши, белый или серый (заяц)
- Жёлтый, полосатый, рычит, символ года (тигр)
- Бурый, косматый зимой спит (медведь)
– А сейчас – заключительный разговор. Подведём
итог нашей работе.
– Что узнали нового?
– Что получилось легко?
– В какие моменты урока испытывали трудности?
– Как вы сможете использовать свой новый опыт?
9. Комментарии к домашнему заданию
Слайд 17
Выполнить упражнения в рабочей тетради к §16.
10. Рефлексия
– Закончите предложения:
Слайд 18
Я работал с ______________ настроением.
Я _____________ доволен собой.
Я бы хотел стать более ____________.
Слайд 19
– Дорогие ребята, мне хочется поблагодарить
вас за активность и инициативу. Наша совместная
работа заканчивается, но наше сотрудничество
продолжается.
– Я хочу похлопать Насте, потому что мне
понравилось, как она работала сегодня на уроке.
– Настя, а чья работа понравилась тебе? (Поочерёдно
дети хлопают друг другу, пока весь класс не будет
хлопать последнему ученику)
Источник
