Какое количество идеального газа содержится в сосуде объемом
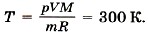
В сосуде содержится гелий под давлением кПа. Концентрацию гелия увеличили в раза, а среднюю кинетическую энергию его молекул уменьшили в раза.
Определите установившееся давление газа.
Ответ дайте в кПа.
Это задание решали 150 раз. С ним справились 35% пользователей.
Газ, который можно считать идеальным, перешел из состояния в состояние
Определите отношение давлений газа в начальном и конечном состояниях
Масса газа постоянна.
Это задание решали 41 раз. С ним справились 29% пользователей.
На рисунке изображен процесс перехода идеального газа постоянной массы из состояния в состояние
Найдите, во сколько раз изменилась абсолютная температура газа в состоянии по сравнению с абсолютной температурой в состоянии
Это задание решали 80 раз. С ним справились 73% пользователей.
Это задание решали 36 раз. С ним справились 61% пользователей.
На рисунке изображена зависимость давления от абсолютной температуры для
постоянной массы идеального газа.
Объем газа в состоянии равен л.
Определите объем газа (в л) в состоянии
Это задание решали 53 раза. С ним справились 70% пользователей.
Это задание решали 47 раз. С ним справились 51% пользователей.
моль идеального газа изохорно нагревают на К, при этом его давление
увеличивается в раза.
Какова первоначальная абсолютная температура газа?
Это задание решали 41 раз. С ним справились 37% пользователей.
Во сколько раз увеличится значение квадрата среднеквадратичной скорости
движения молекул, если для данной массы газа его внутренняя энергия
увеличится в раза?
Это задание решали 46 раз. С ним справились 65% пользователей.
Давление идеального газа в герметичном сосуде объемом л равно кПа.
Каким будет давление (в кПа) этого газа, если объем сосуда изотермически
увеличить в раза?
Это задание решали 54 раза. С ним справились 61% пользователей.
Давление газа на стенки герметичного баллона равно кПа.
Чему будет равно давление этого газа (в кПа) при увеличении квадрата средней скорости движения молекул газа в раза?
Это задание решали 41 раз. С ним справились 76% пользователей.
В ходе эксперимента давление разреженного газа в сосуде увеличилось в раза, а средняя энергия теплового движения его молекул уменьшилась в раза.
Во сколько раз увеличилась концентрация молекул газа в сосуде?
Это задание решали 115 раз. С ним справились 23% пользователей.
В сосуде находится идеальный газ при температуре C. Концентрация молекул этого газа равна м
Определите давление (в кПа), создаваемое
газом на стенки сосуда.
Постоянная Больцмана равна Дж/К.
Это задание решали 72 раза. С ним справились 56% пользователей.
В ходе эксперимента давление разреженного газа в сосуде уменьшилось в
раза.
Во сколько раз уменьшилось среднее значения квадрата скорости
движения молекул этого газа, если его концентрация осталась неизменной?
Это задание решали 22 раза. С ним справились 41% пользователей.
Идеальный газ находится в закрытом сосуде.
Во сколько раз уменьшится давление в этом сосуде, если его наполнить другим идеальным газом, молярная масса которого в два раза больше?
Абсолютная температура и плотность газа в
сосуде не изменились.
Это задание решали 61 раз. С ним справились 79% пользователей.
При проведении опыта в сосуд постоянного объема закачали воздух и одновременно сосуд с воздухом нагрели. В конечном равновесном состоянии воздуха в сосуде абсолютная температура повысилась в раза, а его давление возросло в раза по сравнению с начальными значениями.
Во сколько раз увеличилась масса воздуха в сосуде?
Это задание решали 70 раз. С ним справились 57% пользователей.
Источник
Задача 13.1.1. С идеальным газом происходит процесс, в котором кон-центрация молекул газа (при неизменной массе) увеличилась в 2 раза, абсолютная температура увеличилась в 3 раза. При этом давление идеального газа:
Увеличилось в 6 раз | Увеличилось в 3 раза |
Увеличилось в 3/2 раза | Уменьшилось в 3/2 раза |
Задача 13.1.3. В сосуде неизменного объема содержится идеальный газ в количестве 2 моль. Как надо изменить абсолютную температуру газа в сосуде, чтобы при добавлении в сосуд еще одного моля газа давление в сосуде увеличилось в 3 раза?
Уменьшить в 2 раза | Увеличить в 2 раза |
Уменьшить в 3 раза | Увеличить в 3 раза |
Задача 13.1.4. При нагревании идеального газа в сосуде его абсолютная температура увеличилась в 2,5 раза, а давление выросло в 2 раза. Во сколько раз уменьшилась масса газа в сосуде? Объем сосуда и химический состав газа не изменялся.
В 5 раз | В 8 раз |
В 1,25 раза | Не изменилась |
Задача 13.1.5.  Если полностью опустить запаянную с одного конца стеклянную трубку в воду, выпустить из нее воздух, заполнив водой, и аккуратно вытаскивать из воды запаянным концом вверх, то вода останется в трубке и будет подниматься вместе с ней (см. рисунок). Это происходит:
Если полностью опустить запаянную с одного конца стеклянную трубку в воду, выпустить из нее воздух, заполнив водой, и аккуратно вытаскивать из воды запаянным концом вверх, то вода останется в трубке и будет подниматься вместе с ней (см. рисунок). Это происходит:
Благодаря тому, что «природа боится пустоты»
Благодаря всасывающей силе вакуума
Благодаря взаимодействию воды с верхним участком трубки (выделен жирным на рисунке)
Благодаря давлению атмосферного воздуха на поверхность воды в сосуде и закону Паскаля
Задача 13.1.6. 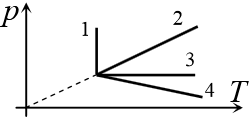 На рисунке приведены графики четырех процессов – 1, 2, 3 и 4, – происходящих с идеальным газом. Масса газа не меняется в течение всех этих процессов. В каком из этих процессов меняются и давление, и объем, и температура газа?
На рисунке приведены графики четырех процессов – 1, 2, 3 и 4, – происходящих с идеальным газом. Масса газа не меняется в течение всех этих процессов. В каком из этих процессов меняются и давление, и объем, и температура газа?
Задача 13.1.7. 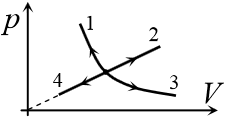 На рисунке приведены графики четырех процессов – 1, 2, 3 и 4, – происходящих с идеальным газом. В процессах 2 и 4 зависимость давления от объема прямо пропорциональная, в процессах 1 и 3 – обратно пропорциональная. Масса газа не меняется в течение всех этих процессов. Какой из них является изотермическим расширением?
На рисунке приведены графики четырех процессов – 1, 2, 3 и 4, – происходящих с идеальным газом. В процессах 2 и 4 зависимость давления от объема прямо пропорциональная, в процессах 1 и 3 – обратно пропорциональная. Масса газа не меняется в течение всех этих процессов. Какой из них является изотермическим расширением?
Задача 13.1.8. 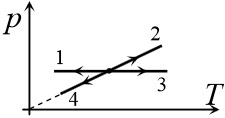 На рисунке приведены графики четырех процессов – 1, 2, 3 и 4, – происходящих с идеальным газом. Масса газа не меняется в течение всех этих процессов. Какой из них является изохорическим охлаждением?
На рисунке приведены графики четырех процессов – 1, 2, 3 и 4, – происходящих с идеальным газом. Масса газа не меняется в течение всех этих процессов. Какой из них является изохорическим охлаждением?
Задача 13.1.9. В сосуде объемом 2 м3 находится 0,14 кг азота при температуре 800 К. Найти давление азота, считая его идеальным газом.
Задача 13.1.10. В сосуде объемом 8,31 л находится идеальный газ при температуре 127 °С под давлением 100 кПа. Какое количество вещества газа содержится в сосуде?
0,25 моль | 0,5 моль | 0,75 моль | 1 моль |
Источник
Глава 10. Уравнение состояния идеального газа. Газовые законы
При решении задач по данной теме надо чётко представлять себе начальное состояние системы и какой процесс переводит её в конечное состояние. Одна из типичных задач на использование уравнения состояния идеального газа: требуется определить параметры системы в конечном состоянии по известным макроскопическим параметрам в её начальном состоянии.
Задача1. Воздух состоит из смеси газов (азота, кислорода и т. д.). Плотность воздуха ρ0 при нормальных условиях (температура t0 = 0 °С и атмосферное давление р0 = 101 325 Па) равна 1,29 кг/м3. Определите среднюю (эффективную) молярную массу М воздуха.
Р е ш е н и е. Уравнение состояния идеального газа при нормальных условиях имеет вид 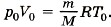 Здесь R = 8,31 Дж/(моль • К) и Т0 = 0 °С + 273 °С = 273 К, М — эффективная молярная масса воздуха. Эффективная молярная масса смеси газов — это молярная масса такого воображаемого газа, который в том же объёме и при той же температуре оказывает на стенки сосуда то же давление, что и смесь газов, в данном случае воздух. Отсюда
Здесь R = 8,31 Дж/(моль • К) и Т0 = 0 °С + 273 °С = 273 К, М — эффективная молярная масса воздуха. Эффективная молярная масса смеси газов — это молярная масса такого воображаемого газа, который в том же объёме и при той же температуре оказывает на стенки сосуда то же давление, что и смесь газов, в данном случае воздух. Отсюда
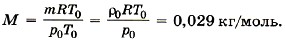
Задача2. Определите температуру кислорода массой 64 г, находящегося в сосуде объёмом 1 л при давлении 5 • 106 Па. Молярная масса кислорода М = 0,032 кг/моль.
Р е ш е н и е. Согласно уравнению Менделеева—Клапейрона 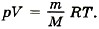
Отсюда температура кислорода 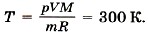
Задача3. Определите плотность азота при температуре 300 К и давлении 2 атм. Молярная масса азота М = 0,028 кг/моль.
Р е ш е н и е. Запишем уравнение Менделеева—Клапейрона: 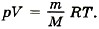
Разделив на объём левую и правую части равенства, получим
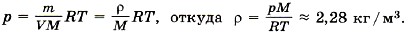
Задача4. Определите, на сколько масса воздуха в комнате объёмом 60 м3 зимой при температуре 290 К больше, чем летом при температуре 27 °С. Давление зимой и летом равно 105 Па.
Р е ш е н и е. Запишем уравнение Менделеева—Клапейрона: 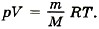
Из этого уравнения выразим массу газа: 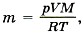 где T принимает значения Т1 и Т2 — температуры воздуха зимой и летом. Молярная масса воздуха М = 0,029 кг/моль. Температура воздуха летом Т2 = 27 °С + 273 °С = 300 К.
где T принимает значения Т1 и Т2 — температуры воздуха зимой и летом. Молярная масса воздуха М = 0,029 кг/моль. Температура воздуха летом Т2 = 27 °С + 273 °С = 300 К.
Таким образом,
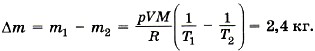
Задачи для самостоятельного решения
1. Чему равен объём идеального газа в количестве одного моля при нормальных условиях?
2. Определите массу воздуха в классе размером 6x8x3 м при температуре 20 °С и нормальном атмосферном давлении. Молярную массу воздуха примите равной 0,029 кг/моль.
3. В баллоне вместимостью 0,03 м3 находится газ под давлением 1,35 • 106 Па при температуре 455 °С. Какой объём занимал бы этот газ при нормальных условиях (t0 = 0 °С, р — 101 325 Па)?
4. Выразите среднюю квадратичную скорость молекулы через универсальную газовую постоянную и молярную массу.
5. При переходе газа определённой массы из одного состояния в другое его давление уменьшается, а температура увеличивается. Как изменяется его объём?
Образцы заданий ЕГЭ
С1. При температуре 240 К и давлении 166 кПа плотность газа равна 2 кг/м3. Чему равна молярная масса этого газа?

С2. Плотность идеального газа меняется с течением времени так, как показано на рисунке. Температура газа при этом постоянна. Во сколько раз давление газа при максимальной плотности больше, чем при минимальной?
С3. Газ находится в баллоне вместимостью 8,31 л при температуре 127 °С и давлении 100 кПа. Какое количество вещества содержится в газе?
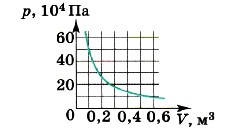
С4. На рисунке показан график изменения давления идеального газа при его расширении. Какое количество газообразного вещества (в молях) содержится в этом сосуде, если температура газа постоянна и равна 300 К?

С5. На рисунке показан график зависимости давления газа в запаянном сосуде от его температуры. Объём сосуда равен 0,4 м3. Сколько молей газа содержится в этом сосуде?
Источник
За это задание ты можешь получить 1 балл. Уровень сложности: базовый.
Средний процент выполнения: 72.5%
Ответом к заданию 8 по физике может быть целое число или конечная десятичная дробь.
Задачи для практики
Задача 1
Сосуд вместимостью 12 л, содержащий газ при давлении 0,4 МПа, соединяют с другим сосудом, из которого откачан воздух. Найдите конечное значение давления. Процесс изотермический. Вместимость второго сосуда равна 3,0 л. Ответ выразите в (МПа).
Решение
Дано:
$V_1=12·10^{-3}м^3$
$V_2=3·10^{-3}м^3$
$p_1=0.4·10^6$Па
$T_1=T_2=T=const$
$p_2-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: ${p_1V_1}/{T_1}={p_2(V_2+V_1)}/{T_2}$(1), т.к. $T_1=T_2=T=const$, можно записать: $p_1V_1=p_2(V-2+V_1)$(2), откуда $p_2={p_1V_1}/{(V_2+V_1)}={0.4·10^6·12·10^{-3}}/{15·10^{-3}}=0.32$МПа.
Ответ: 0.32
Задача 2
Газ, занимающий объём 12,32 л, охладили при постоянном давлении на 45 К, после чего его объём стал равен 10,52 л. Какова была первоначальная температура газа? Ответ выразите в (К).
Решение
Дано:
$∆T=45K$
$V_1=12.32·10^{-3}м^3$
$V_2=10.52·10^{-3}м^3$
$p_1=p_2=p=const$
$T_1-?$
Решение:
Из уравнения Менделеева-Клайперона имеем: ${p_1V_1}/{T_1}={p_2V_2}/{T_2}$(1), учитывая, что $p=const$, имеем: ${pV_1}/{T_1}={pV_2}/{T_2}$ или $V_1T_2=V_2T_1$(2). Так как газ охладили, то $T_2=T_1-∆T$(3). Подставим (3) в (2): $V_1T_1-V_1∆T=V_2T_1⇒T_1={V_1∆T}/{(V_1-V_2)}={12.32·10^{-3}·45}/{1.8·10^{-3}}=308K$.
Ответ: 308
Задача 3
В закрытом сосуде находится 120 г газа при комнатной температуре. Какая масса газа вытечет из сосуда, если после открытия крана давление в сосуде понизится в 4 раза? Ответ выразите в (кг).
Решение
Дано:
$T=20+273=293К$
$P_2={P_1}/{4}$
$m_1=0.12$кг
$∆m-?$
$T=const$
$V=const$
Решение:
Зная уравнение Менделеева-Клайперона составим систему 1 и 2.
${tableP_1V={m}/{M}·RT_1; P_2V={m}/{M}·RT_2;$, то $4={m_1}/{m_2}; m_2=0.03$.
$∆m=m_1-m_2=0.12-0.03=0.09$кг.
Ответ: 0.09
Задача 4
В сосуде содержится неон при температуре −3◦С. Во сколько раз увеличится средняя кинетическая энергия теплового движения молекул неона, если его нагреть до 132◦С? В ответе запишите в(во) сколько раз(а).
Решение
Дано:
$t_1=-3+273=270К$
$T_2=132+273=405K$
${E_{к_2}}/{E_{к_1}}$
Решение:
$E_к={3}/{2}KT$.
${E_{к_2}}/{E_{к_1}}={T_2}/{T_1}={405}/{270}=1.5$
Ответ: 1.5
Задача 5
В сосуде содержится аргон при температуре 327◦С. Какая абсолютная температура установится, если концентрацию аргона увеличить в 2 раза, а давление уменьшить в 3 раза? Ответ выразить в (K).
Решение
Дано:
$T^1_{Ар}=327+273=600K$
$n_2=2·n_1$
$P_2={P_1}/{3}$
$T_2$
Решение:
Запишем уравнение состояния газа дважды:
${tableP_1=n_1·K·T_1; P_2=n_2·K·T_2;$ $⇒T_2={T_1}/{2}={600}/{6}=100K$.
Ответ: 100
Задача 6
В сосуде содержится водород, манометр показывает 0,5 атмосферы. Какое установится давление, если концентрацию водорода увеличить в 6 раз, а среднюю кинетическую энергию теплового движения его молекул уменьшить в 4 раза? Ответ выразите в (кПа).
Решение
Дано:
$P_1=0.5·P_{атм}$
$n_2=6·n_1$
$E_{к_2}={E_{к_1}}/{4}$
$P_{атм}=10^5$
Решение:
${tableP_1={2}/{3}·n_1·E_{к_1}; P_2={2}/{3}·n_2·E_{к_2};$ $⇒{0.5·10^5}/{P_2}={1}/{6}:{1}/{4}$.
Для 1 и 2 случая $P_2=75·10^3$Па.
Ответ: 75
Задача 7
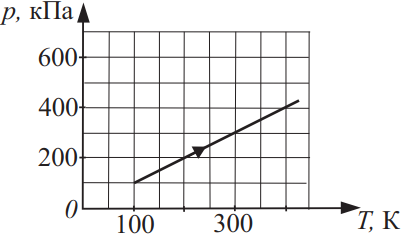
На рисунке показан график изменения давления 10 моль газа при изохорном нагревании. Найдите объём этого газа. Ответ округлите до целого, выразив в (дм3).
Решение
Дано:
$V-?$
$V=const$
$υ=10$моль
Решение:
Из уравнения Менделеева-Клайперона $pV=υRT⇒V={υRT}/{p}={10·8.31·100}/{100·10^3}=83.1дм^3$
Ответ: 83
Задача 8
1 моль идеального газа изохорно охлаждают на 200 К, при этом его давление уменьшается в 3 раза. Найдите первоначальную температуру газа. Ответ выразите в (К).
Решение
Дано:
$υ=1$моль
$υ=const$
$∆T=200K$
${P_1}/{3}=P_2$
$T_0-?$
Решение:
${P_1}/{T_1} > {P_2}/{T_2}$ – изохорный.
$T_0={P_1}/{P_2}·T_2=3(1-200)$
$2T_0=600$
$T_0=300K$
Ответ: 300
Задача 9
Определите плотность азота при температуре 27◦С и давлении 150 кПа. Ответ округлите до десятых. Ответ выразите в (кг/м3).
Решение
Дано:
$T=27°C=300K$
$P=150$кПа
$v=2(Т_2)$
$ρ-?$
Решение:
$PV={m}/{M}·RT$
$ρ·R·T=P·M$
$ρ={P·M}/{R·T}={150·10^3·0.028}/{8.31·300}=1.7кг/м^3$.
Ответ: 1.7
Задача 10
Определите температуру азота, имеющего массу 4 г, занимающего объём 831 см3 при давлении 0,2 МПа. Ответ выразите в (К).
Решение
Дано:
$N_2T-?$
$m=4·10^{-3}кг$
$V=831см^3$
$P=0.2·10^6$
$T_?$
Решение:
По закону Менделеева-Клайперона $pV={m}/{M}R·T; T={pv·M}/{m·R}$
$T={0.2·10^6·8.31·0.028}/{4·10^{-3}·8.31}=140K$
Ответ: 140
Задача 11
При повышении температуры идеального газа на 100 К среднеквадратичная скорость движения молекул выросла с 200 м/с до 600 м/с. Насколько надо понизить температуру газа, чтобы среднеквадратичная скорость уменьшилась с 600 м/с до 400 м/с? В ответе запишите на сколько (K).
Решение
Дано:
$∆T=100K↑$
$υ_{cр_1}=200$м/с
$υ_{cр_2}=600$м/с
$∆T-?↓$
$υ_{cр_2}=600$м/с
$υ_{cр_3}=400$м/с
Решение:
В первом процессе $T_1={υ_1^2μ}/{3R}$
$T_2={υ_2^2μ}/{3R}$
$∆T_1=T_2-T_1={μ}/{3R}·(υ_2^2·r_1^2)$
${μ}/{3R}={∆T}/{υ_2^2-r_1^2}={1}/{3200}$
Тогда $∆T_2={μ}/{3R}(υ_2^2-υ_3^2)={1}/{3200}(400^2-600^2)=62.5K$
Ответ: 62.5
Задача 12
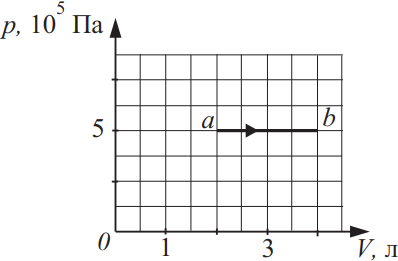
Идеальный газ в количестве 1,5 моль совершает процесс, изображённый на рисунке. Какова температура газа в состоянии b? Ответ выразите в (K), округлив до сотых.
Решение
Дано:
$v=1.5$моль
$T_в-?$
$P=const=10^5$Па
$V_a=2л$
$V_в=4л$
Решение:
По закону Менделеева-Клайперона для точки а и в составим систему: ${tableP·V_a=vRT_a(1); P·V_в=vRT_в(2);$. Из (2) найдем: $T_в={5·10^5·4·10^{-3}}/{1.5·8.31}=160.45K$
Ответ: 160.45
Задача 13
Концентрация молекул идеального одноатомного газа равна 2 · 1024 м−3. Какое давление оказывает газ на стенки сосуда, если при этом средняя кинетическая энергия молекулы равна 1,5 · 10−20 Дж? Ответ выразите в (кПа).
Решение
Дано:
$n=2·10^{24}м^{-3}$
$E_к=1.5·10^{-20}$
$P-?$
Решение:
${tableE_к={3}/{2}KT={3}/{2}K{P}/{nK}; P=nKT;$
Выразим и получим формулу из основ МКТ: $p={E_к·2n}/{3}={1.5·10^{-20}·2·2·10^{24}}/{3}=20$кПа.
Ответ: 20
Задача 14
Температура идеального газа понизилась от 700◦С до 350◦С. Во сколько раз при этом изменилась средняя кинетическая энергия движения молекул газа? Ответ округлить до сотых
Решение
Дано:
$T_1=700°C+273=973K$
$T_2=350°C+273=623K$
${E_1}/{E_2}-?$
Решение:
Из основ молекулярно-кинетической теории известно, что ${E_1}/{E_2}={T_1}/{T_2}$
${E_1}/{E_2}={973}/{623}=1.56$
Ответ: 1.56
Задача 15
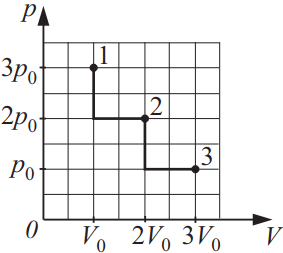
На диаграмме pV изображены процессы перевода некоторой неизменной массы идеального газа из состояния 1 в состояние 3. Начальная (T1) и конечная (T3) температуры связаны между собой соотношением T3/T1…
Решение
Дано:
$Т_1-$начальная
$Т_2$конечная
${T_3}/{T_1}-?$
Решение:
Запишем уравнение Менделеева-Клайперона для начальной и конечной точки состояния: ${table.{p_1·V_1}/{T_1}=υR; .{p_3·V_3}/{T_3}=υR;$.
$⇒{p_1·V_1}/{T_1}={p_3·V_3}/{T_3}⇒{T_3}/{T_1}={p_3·V_3}/{p_1·V_1}⇒{T_3}/{T_1}={p_0·3V_0}/{3p_0·V_0}=1$.
Ответ: 1
Задача 16
При какой температуре молекулы гелия имеют такую же среднюю квадратичную скорость, как молекулы водорода при 27◦С? Ответ выразите в (◦ С).
Решение
Дано:
$t_{H_2}=27°C$
$_{He}=_{H_2}$
$t_{He}-?$
Решение:
Средняя квадратичная скорость молекул гелия и водорода ($He$ и $H_2$) равны соответственно: $_{He}=√{{3RT_{He}}/{μ_{He}}}$, где $T_{He}=t_{He}+273°C$
$_{H_2}=√{{3RT_{H_2}}/{μ_{H_2}}}$, где $T_{H_2}=t_{H_2}-273°C$
Молярные массы гелия $He$ и водорода $H_2$ равны соответственно: $μ_{He}=4·10^{-3}кг/моль; μ_{H_2}=2·10^{-3}кг/моль; T_{H_2}=27°C+273°C=300K$
$√{{3RT_{He}}/{μ_{He}}}=√{{3RT_{H_2}}/{μ_{H_2}}}⇒{3RT_{He}}/{μ_{He}}={3RT_{H_2}}/{μ_{H_2}}⇒T_{He}={T_{H_2}·μ_{He}}/{μ_{H_2}}={300·4·10^{-3}}/{2·10^{-3}}=600K$, тогда $t_{He}=T_{He}-273°C=600°C-273°C=327°C$
Ответ: 327
Задача 17
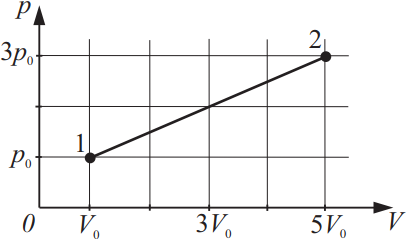
На рисунке изображено изменение состояния идеального газа. Во сколько раз температура в состоянии 2 больше, чем температура в состоянии 1?
Решение
Дано:
$p_1=p_0$
$V_1=V_0$
$p_2=3p_0$
$V_2=5V_0$
${T_2}/{T_1}-?$
Решение:
Из уравнения Менделеева-Клайперона: $pV={m}/{μ}RT$(1), следует равенство ${p_1V_1}/{T_1}={p_2V_2}/{T_2}⇒{p_0V_0}/{T_1}={3p_0·5V_0}/{T_2}$(2).
Из (2) имеем: $p_0V_0T_2=3p_0V_0·5T_1$
$T_2=3·5T_1⇒T_2=15T_1$ или ${T_2}/{T_1}=15$
Ответ: 15
Источник
