Какое из свойств электростатического поля указывает на то что оно является потенциальным
Определение 1
Потенциальное (консервативное) поле − это поле, в котором работа при перемещении зависит только лишь от конечной и начальной точки пути и не зависит от траектории движения тела.
Что такое потенциальное поле
Есть и другое абсолютно равнозначное определение потенциальности поля (консервативной силы).
Определение 2
Поле называется потенциальным, если при перемещении по любому замкнутому контуру работа сил поля равняется 0.
Известно, что сила гравитации FG~1r2, которая убывает обратно пропорционально квадрату расстояния, является потенциальной, при этом ее потенциальность обусловлена именно обратно пропорциональной зависимостью от расстояния. Сила Кулона тоже обратно пропорциональна квадрату расстояния. Напомним закон Кулона FE~1r2. Все математическое описание потенциала создавалось при изучении сил гравитации. Понятие о потенциале появилось в работах Ж. Л. Лагранжа в 1777 году. Определение «потенциал» было введено в науку намного позже Дж. Грином и К. Ф. Гауссом.
Определение 3
На основе принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.
Доказательство 1
Легко докажем это математически. Циркуляция вектора напряженности поля точечного заряда Ei→ по любому замкнутому контуру равняется 0:
∮LEi→ds→=0.
Если поле создает N точечных зарядов, тогда по принципу суперпозиции результирующее поле находим как:
E→=∑iEi→.
Находим интеграл:
∮LE→ds→=∮L∑iEi→ds→=∑i∮LEi→ds→=∑i0=0.
Приведенный выше критерий потенциальности поля не дифференциален, поэтому его трудно применять. Нужно проверять равенство 0 работы по замкнутому контуру. А это означает, что необходимо анализировать бесконечное число циклов, что, в конечном итоге, невозможно. Критерий потенциальности применим лишь в случае, когда известна аналитическая формула работы, что не всегда возможно. Поэтому нужно отыскать другой критерий потенциальности поля, который был бы прост в применении. Данным критерием является дифференциальная формулировка. Она определяется при помощи понятия ротор вектора rot A→.
Что такое ротор. Практические задачи
Определение 4
Ротор − это вектор, проекция которого на направление единичного вектора n→ определяется таким образом:
rotnA→=lim∆S→0∮A→·ds→∆S,
где ∆S − это площадь, которая лежит в плоскости перпендикулярной к n→, ограниченная малым контуром L, на контуре L − это направление положительного обхода связано с n→ правилом правого винта.
Замечание 1
Обращаем внимание, что в формуле большой буквой S обозначена площадь, а маленькой буквой s − линейное перемещение.
Ротор описывает интенсивность «завихрения» вектора. На практике при вычислении ротора применяют следующие формулы:
rot A→=∇×A→=i→j→k→∂∂x∂∂y∂∂zAxAyAk.
Независимость работы от пути перемещения заряда в электростатическом поле выражается формулой:
∫AL1BE→·ds→=∫AL2BE→·ds→.
где L1 и L2− это различные пути между точками А и В. При замене местами пределов интегрирования получаем:
∫AL2BE→·ds→=-∫BL2AE→·ds→.
Выражение ∫AL1BE→·ds→=∫AL2BE→·ds→ представим в виде:
∫AL1BE→·ds→=∫BL2AE→·ds→=∮LE→·ds→=0.
где L=L1+L2. Применяем формулу Стокса:
∫Srot A→·dS→=∮LA→·ds→,
к уравнению выше, получаем:
∮LE→·ds→=∫Srot E→·dS→=0,
где S− это поверхность, ограниченная контуром L. Поскольку поверхность произвольная, то интеграл в выражении ∮LE→·ds→=∫Srot E→·dS→=0 может равняться 0, только если равняется 0 подынтегральное выражение, а поскольку dS→≠0 то есть:
Определение 5
rot E→=0.
Это дифференциальная формулировка потенциальности электростатического поля.
Пример 1
Необходимо найти rotn υ→ для точек оси вращения, если υ→ − это вектор скорости точек твердого тела, вращающегося с угловой скоростью ω вокруг оси коллинеарной n→
Решение
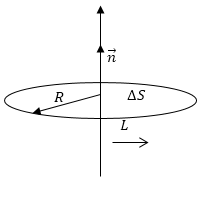
Рисунок 1
В качестве контура L выберем окружность радиусом R с центром на оси вращения, перпендикулярную оси (рисунок 1). Известно, что:
υ=ωR,∆S=πR2.
Обозначим υds. ds как скалярное значение элемента окружности. Для этого используем формулу определения ротора, получаем:
rotn υ→=limR→0∮ωR→·ds→πR2=limR→0ωR2πRπR2=2ω,
где ∮ds=2πR − это длина окружности.
Ответ: Ротор линейной скорости точек вращающегося тела равняется rotn υ→=2ω.
Пример 2
Необходимо доказать, что из условия потенциальности поля следует: тангенциальные составляющие напряженности электростатического поля непрерывны.
Решение
Поскольку электростатическое поле потенциально, тогда выполняется равенство:
A=∮LE→ds→=0.
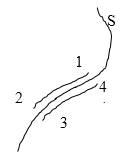
Рисунок 2
Определение 6
Тангенциальные составляющие − это касательные к произвольной поверхности в любой ее точке. Непрерывность значит, что значения касательных составляющих напряженности одинаковы по обеим сторонам поверхности.
Пример 3
Допустим обратное. Пускай вдоль поверхности S (рисунок 2) непрерывности нет. Это означает, что если 1, 2 и 3, 4 разделенные поверхностью S, но бесконечно близкие друг к другу точки, тогда работа электростатических сил на пути 1→2 отличается на конечную величину от работы тех же сил на пути 3→ 4. Так как мы считаем, что отрезки 1→2 и 3→ 4 бесконечно малы, силы конечны, значит, и работа, которую выполняют электрические силы на заданных отрезках, бесконечно малая величина. Выходит, что работа на пути 1→2→3→4→1 не должна равняться 0. То есть работа сил по перемещению пробного заряда по замкнутому контуру не равняется 0. Это невозможно, поскольку электростатическое поле потенциально. Мы показали, что тангенциальные составляющие напряженности электростатического поля не непрерывны.
Источник
Потенциальность электростатического поля
Пусть точечный заряд $q$ перемещается по произвольной траектории в электростатическом поле из точки $1$ в точку $2$ под действием нескольких сил. Нас интересует сила $vec{F_{э}}$, действующая на заряд со стороны электростатического поля. При заданном перемещении заряда она совершает работу $A_{э}$.
Электростатическое поле обладает удивительным свойством. Оказывается, что эта работа не зависит от траектории, по которой перемещается заряд в электростатическом поле, а определяется только его начальным и конечным положениями (расположением точек $1$ и $2$). Это свойство называется потенциальностью (консервативностью). Следует понимать, что именно электростатическое поле является потенциальным, произвольное электрическое $-$ нет.
Потенциальная энергия точечного заряда
В связи с этим свойством для удобного расчета работы $A_{э}$ сил электростатического поля вводится понятие потенциальной энергии $textrm{П}$ точечного заряда в электростатическом поле.
Потенциальной энергией $textrm{П}$ точечного заряда $q$ в электростатическом поле называется скалярная (числовая) функция $textrm{П}=textrm{П}(x,y,z)$ координат пространства такая, что работа сил $A_{э}$ электростатического поля при перемещении этого заряда по произвольной траектории из точки $1$ в точку $2$ равна разности значений этой функции в этих точках:
$A_{э}=textrm{П}_1-textrm{П}_2{textrm{,}}$
где $textrm{П}_1=textrm{П}(x_1,y_1,z_1)$ $-$ потенциальная энергия в точке $1$, $textrm{П}_2=textrm{П}(x_2,y_2,z_2)$ $-$ потенциальная энергия в точке $2$.
Из определения видно, что потенциальная энергия $textrm{П}$ определяется с точностью до постоянной. Чтобы определить значение потенциальной энергии, требуется выбрать нуль потенциальной энергии (точку отсчета). Понятно, что физический смысл имеет лишь разность потенциальных энергий.
Потенциальная энергия $textrm{П}$ точечного заряда зависит как от электростатического поля, так и от величины самого заряда. Выходит, различные точечные заряды в одной и той же точке имеют разные потенциальные энергии, что не очень удобно. В связи с этим было введено понятие электрического потенциала $varphi$. Каким образом? Было установлено, что отношение $textrm{П}/q$ не зависит от величины $q$, следовательно, является характеристикой только электростатического поля. Ее и назвали электрическим потенциалом $varphi$:
$varphi=textrm{П}/q{textrm{.}}$
Электрический потенциал $varphi$ $-$ энергетическая характеристика электростатического поля. Также потенциал $varphi$ можно определить подобно тому, как была определена потенциальная энергия $textrm{П}$.
Потенциал электростатического поля
Потенциалом $varphi$ электростатического поля называется скалярная (числовая) функция $varphi=varphi(x,y,z)$ координат пространства такая, что работа сил $A_{э}$ электростатического поля при перемещении произвольного точечного заряда $q$ по произвольной траектории из точки $1$ в точку $2$ равна разности значений этой функции в этих точках, умноженной на $q$:
$A_{э}=q{cdot}(varphi_1-varphi_2){textrm{,}}$
где $varphi_1=varphi(x_1,y_1,z_1)$ $-$ потенциальная энергия в точке $1$, $varphi_2=varphi(x_2,y_2,z_2)$ $-$ потенциальная энергия в точке $2$.
Из определения видно, что потенциал $varphi$ электростатического поля определяется с точностью до постоянной. Чтобы определить значение потенциала, требуется выбрать нуль потенциальной энергии (точку отсчета). Понятно, что физический смысл имеет лишь разность потенциалов.
Выводы.
Работа $A_{э}$ сил электростатического поля по перемещению точечного заряда $q$ не зависит от траектории его движения, а определяется только начальным и конечным положениями заряда.
Для удобного расчета работы сил электростатического поля вводятся понятия потенциальной энергии $textrm{П}$ и потенциала $varphi$: $A_{э}=textrm{П}_1-textrm{П}_2=q{cdot}(varphi_1-varphi_2)$.
Потенциальная энергия $textrm{П}$ зависит как от заряда $q$, так и от электростатического поля. Потенциал электростатического поля $varphi$ зависит только от свойств самого поля.
Источник
Какое из соотношений определяет длину волны де Бройля: D) l=h/p
Какое из указанных свойств не относится к электрическим зарядам: B) Заряд является основной величиной, определяющей электромагнитное взаимодействие
Какое из уравнений описывает состояние для одного моля реального газа в критической точке? E)
Какое из утверждений является верным для случая, когда механическая система является замкнутой? D) суммарный импульс системы остается постоянным
Какое из явлений переноса обусловлено переносом импульса из одного слоя газа в другой ? C) вязкое трение
Какое количество ядер распадается за время равное двум периодам полураспада радиоактивного элемента? D) 75%
Какое количество ядер распадается за время равное периоду полураспада радиоактивного элемента? C) 50%
Какое максимальное значение принимает орбитальное квантовое число l при данном главном квантовом числе n? C) -1
Какое максимальное значение принимает орбитальное квантовое число при данном главном квантовом числе ? C) -1
Какое максимальное число электронов может находиться в p-состоянии атома? C) 6
Какое максимальное число электронов может находиться в S-состоянии атома? B) 2
Какое наибольшее число максимумов можно наблюдать, если плоская монохроматическая волна падает на дифракционную решетку нормально? Период решетки 2 мкм, длина волны о,5 мкм. E) 9
Какое наибольшее число ориентаций в пространстве может иметь спин электрона в атоме? C)2
Какое увеличение дает лупа, оптическая сила которой 8 диоптрий,если расстояние от предмета до лупы 25 см. A) 1
Какое условие является необходимым для того, чтобы происходила дифракция света с длиной волны l в область геометрической тени от отверстия радиуса r? A) r~l
Какое число зон Френеля должно укладываться на узкой щели, чтобы экран оставался темным при падении на щель нормально плоской монохроматической волной? B) 22
Какое число ориентаций в пространстве может принимать вектор орбитального момента импульса электрона в р-состоянии? C) 3
КАКОЙ
Два когерентных световых пучка с оптической разностью хода интерферируют в некоторой точке. Что будет наблюдаться в этой точке? минимум | Для какого термодинамического процесса справедливо выражение ?D) для изотермического | За какое время распадется 100 ядер радионуклида, если его активность 20 Бк? C) 5 с | Интенсивность поляризованного света можно определить по закону: C) Малюса | Как расположены относительно друг друга векторы и электромагнитной волны? D) и взаимно перпендикулярны | Как изменится импульс электрона, если его дебройлевская длина волны уменьшилась от 100 мкм до 50 мкм? B) увеличится в 2 раза | Как изменится период колебаний физического маятника, если его перевернуть и подвесить в точке центра качания ? C) не изменится | Какая из указанных на рисунке линий излучения атома водорода соответствует наибольшей частоте излучения? D) 4 | Какая связь существует, в соответствии с атомной теорией Бора, между импульсом электрона в атоме и радиусом его орбиты? B) р ~ 1/r | Какова оптическая разность хода двух когерентных монохроматических волн в веществе, если разность фаз 0,6p? 0,3l |
Источник
3 ПОТЕНЦИАЛЬНЫЙ ХАРАКТЕР ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
В данном разделе мы будем изучать свойство потенциальности на примере электростатического поля в вакууме, созданного неподвижными электрическими зарядами. Далее мы увидим, что существуют не только потенциальные, но и вихревые электрические поля, например, индукционное электрическое поле. Такое вихревое электрическое поле порождается магнитным полем, изменяющимся с течением времени, в соответствии с законом электромагнитной индукции Фарадея.
Рассмотрим точечную заряженную частицу, находящуюся в вакууме во внешнем электростатическом поле с напряженностью 
. При перемещении частицы, имеющей заряд q, из точки 1 в точку 2 электростатические силы совершают работу (рисунок 4)
Рисунок 4 – Траектория перемещения точечной заряженной частицы во внешнем электростатическом поле
, (3.1)
где 
– тангенциальная составляющая вектора 
внешнего электростатического поля относительно элемента траектории 
.
Поле некоторых сил называется потенциальным, если работа, совершаемая при перемещении тела в этом поле, не зависит от формы траектории и определяется только начальным и конечным положением тела.
Электростатическое поле удовлетворяет этому определению и является потенциальным. Поэтому результат интегрирования в формуле (3.1) не изменяется при выборе любой траектории частицы.
Можно дать также и другое определение потенциального поля: это такое поле, в котором работа, совершаемая при перемещении тела по любому замкнутому контуру, равна нулю.
Математически условие потенциальности можно сформулировать, используя понятие циркуляции вектора 
по замкнутому контуру 
:
(3.2)
Соотношение (3.2) называют теоремой о циркуляции вектора 
, или условием потенциальности электростатического поля в интегральной форме.
Хорошо известным примером потенциального поля является гравитационное поле, которое, как и электростатическое поле, убывает обратно пропорционально квадрату расстояния от тела, создающего поле. Можно доказать, что потенциальность поля точечной заряженной частицы связана с обратной квадратичной зависимостью напряженности поля от расстояния. Далее на основании принципа суперпозиции можно утверждать, что произвольное электростатическое поле также является потенциальным.
Циркуляцию некоторого вектора 
по замкнутому контуру можно преобразовать с помощью теоремы Стокса
, (3.3)
где 
– ротор вектора 
, который можно представить в виде векторного произведения оператора «набла» на вектор 
;
– орты декартовой системы координат x, y, z;
– поверхность произвольной формы, границей которой является контур , положительная нормаль к поверхности образует с направлением обхода контура правовинтовую систему.
Для выполнения теоремы Стокса (3.3) необходимо, чтобы на всей поверхности компоненты 
векторного поля 
имели непрерывные частные производные по координатам. Мы предполагаем, что реальные физические поля соответствуют этому требованию, и поэтому для них, в том числе и для вектора напряженности электрического поля 
, теорема Стокса (3.3) является справедливой.
Используя теорему Стокса для вектора , условие потенциальности электростатического поля можно записать в дифференциальной форме:
(3.4)
Из условий (3.3) и (3.4) следует, что поскольку электростатическое поле является потенциальным, то его силовые линии не могут быть замкнутыми. Проведём доказательство от противного и допустим, что существует хотя бы одна замкнутая силовая линия электростатического поля. Выберем эту линию в качестве траектории перемещения точечного заряда. Поскольку для всех элементов такой траектории векторы и совпадают по направлению, то 
, и из формулы (3.1) следует, что электростатическое поле совершило бы положительную, не равную нулю работу при перемещении заряжённой частицы по замкнутой траектории. Но такой вывод противоречил бы условию потенциальности электростатического поля (3.2).
В качестве примера можно рассмотреть самые простые и часто встречающиеся электрические поля: точечного заряда, пары точечных зарядов, нити, цилиндра, сферы, шара, плоскости, плоского слоя. Во всех указанных случаях силовые линии электростатического поля начинаются на положительных зарядах и заканчиваются на отрицательных зарядах, либо уходят в бесконечность, в электростатическом поле замкнутых линий вектора не существует.
Кроме напряженности , электрическое поле характеризуется также скалярным потенциалом 
. Чтобы ввести в рассмотрение скалярный потенциал электростатического поля, можно воспользоваться соотношением, известным из векторного анализа: 
. Это соотношение является тождественным равенством, то есть выполняется для любой функции 
. Сравнивая данное соотношение и формулу (3.4), приходим к выводу, что напряжённость электростатического поля можно представить в виде градиента некоторой функции , которая и называется скалярным потенциалом:
, (3.5)
где 
– градиент скалярной функции j.
Как следует из определения градиента, он является вектором, и это свойство отражено в соотношении (3.5). Единицей измерения потенциала является вольт [В].
В разделе 9 будет показано, что потенциал электростатического поля равен отношению потенциальной энергии заряда, находящегося в данной точке поля, к величине заряда.
Соотношение (3.5) показывает, что напряженность электростатического поля направлена в сторону самого быстрого убывания потенциала в пространстве. Модуль напряженности равен скорости изменения потенциала в направлении, задаваемом градиентом. Напряженность направлена перпендикулярно эквипотенциальной поверхности, то есть такой поверхности, во всех точках которой потенциал имеет одинаковые значения.
В отличие от напряженности, потенциал является неоднозначной функцией и определен с точностью до произвольной постоянной. Чтобы избежать неоднозначности, при решении конкретной задачи производят нормировку потенциала, т. е. приписывают ему определенное значение в некоторой точке. Например, можно считать потенциал равным нулю на поверхности Земли, если рассматривается электрическое поле вблизи земной поверхности. Если заряженные частицы расположены в некоторой ограниченной области, а электрическое поле рассматривается во всем пространстве, то обычно используется другое условие нормировки:
(3.6)
Физический смысл имеет не сам потенциал, а разность потенциалов в двух точках поля. Она численно равна работе, совершаемой полем при перемещении частицы с единичным положительным зарядом из первой точки во вторую:
(3.7)
где учтено соотношение (3.5).
Электростатическое поле является потенциальным, поэтому работа при перемещении частицы в поле не зависит от выбора траектории пробной частицы. Это свойство поля проявляется в формуле (3.7), согласно которой разность потенциалов определяется положением двух точек поля.
В электростатике разность потенциалов двух точек поля называют также электрическим напряжением 
между этими точками. Разность потенциалов и напряжение, так же как и потенциал, измеряются в вольтах. Из соотношения (3.7) следует, что 1В = 1Дж/1Кл.
Важным идеальным примером электростатического поля является однородное поле, напряженность которого не зависит от координат, то есть не изменяется в пространстве в пределах некоторой области. Силовые линии однородного электростатического поля представляют собой параллельные прямые. Густота силовых линий постоянна в пределах той области, в которой выполняется условие однородности поля. Для напряженности однородного электростатического поля из соотношения (3.7) можно получить формулу
, (3.8)
где – разность потенциалов между двумя точками пространства, лежащими на одной силовой линии;
– расстояние между этими точками.
Согласно (3.8), напряженность электрического поля может быть измерена в единицах В/м. Ранее на основании формулы (1.5) мы получили, что единицей измерения напряжённости является Н/Кл.
С некоторыми допущениями можно считать, что однородное поле существует внутри плоского конденсатора вдали от краев его обкладок. Конденсатором называется система, состоящая из двух проводников, имеющих одинаковые по величине, но противоположные по знаку заряды. Эти проводники называются обкладками конденсатора. Если обкладки имеют форму плоскостей, то конденсатор называется плоским. Обычно в конденсаторе расстояние между обкладками значительно уступает по величине линейным размерам обкладок, и этим обеспечивается однородность электростатического поля внутри конденсатора. В случае плоского конденсатора также можно применить формулу (3.8), при этом 
– электрическое напряжение на конденсаторе, – расстояние между его обкладками.
Потенциал поля точечной частицы с зарядом 
при условии нормировки (3.6) равен
, (3.9)
где r – расстояние от заряженной частицы до точки наблюдения, то есть до точки пространства, в которой рассматривается потенциал.
Для скалярного потенциала, так же как и для напряженности электрического поля, применим принцип суперпозиции:
. (3.10)
Согласно (3.10), потенциал электрического поля, создаваемого несколькими заряжёнными частицами в любой точке пространства, равен сумме потенциалов полей всех зарядов, причем потенциал каждого поля вычисляется при условии отсутствия всех других полей.
Используя принцип суперпозиции (3.10), можно вычислить потенциал системы точечных частиц с зарядами 
, расположенных в точках с координатами 
:
, (3.11)
где 
– координаты точки пространства, в которой определяется потенциал.
При непрерывном распределении заряда в некоторой области 
выражение для потенциала имеет вид
, (3.12)
где 
– объемная плотность заряда;
– расстояние от физически малой области 
до точки, в которой вычисляется потенциал.
В заключение данного раздела произведем формальное сравнение математических величин, введенных в рассмотрение в векторном анализе и широко используемых в электромагнетизме:
а) дивергенция вектора – вычисляется в результате дифференцирования векторного поля по пространственным координатам, является скалярной величиной, связана с потоком вектора через замкнутую поверхность и характеризует расходимость линий вектора в пространстве, то есть наличие источников линий вектора в данной точке пространства;
б) ротор вектора – вычисляется в результате дифференцирования векторного поля по пространственным координатам, является векторной величиной, связан с циркуляцией исходного вектора по замкнутому контуру и ассоциируется с замкнутостью линий исходного вектора в пространстве вблизи данной точки;
в) градиент функции – вычисляется в результате дифференцирования скалярной функции по пространственным координатам, является векторной величиной, связан с изменением функции и характеризует максимальную скорость изменения функции в пространстве в окрестности рассматриваемой точки.
Источник