Какое из перечисленных свойств относится к функции y xcosx

Инфоурок
›
Математика
›Презентации›Функция у = cosx её свойства и график.

Описание презентации по отдельным слайдам:
1 слайд

2 слайд

Описание слайда:
изучить функцию У = COS X выяснить ее свойства и вид графика; рассмотреть геометрические преобразования функции косинус. ввести понятие числовой функции косинус;
3 слайд

Описание слайда:
Функция У = COS X определена на всей числовой прямой; множеством её значений является отрезок [ -1; 1]; функция периодическая с периодом 2π; функция чётная, график симметричен относительно оси ОУ;
4 слайд
![Функция У = COS X убывает на отрезке [ 0; π]. При повороте точки (1;0) Вокруг Функция У = COS X убывает на отрезке [ 0; π]. При повороте точки (1;0) Вокруг](https://fs01.infourok.ru/images/doc/58/72316/310/img3.jpg)
Описание слайда:
Функция У = COS X убывает на отрезке [ 0; π]. При повороте точки (1;0) Вокруг начала координат против часовой стрелки на угол от 0 до π абсцисса точки, т.е. cos x, уменьшается от 1 до -1.
5 слайд

6 слайд

Описание слайда:
т.к cos(-x) = cosx функция чётная, значит график симметричен относительно оси ОУ -1
7 слайд

Описание слайда:
Числовая функция, заданная формулой y=cos x, называется косинусом.
8 слайд
![Свойства функции y=cosx 1) D(cosx): (-∞;+∞) 2) E(cosx): [-1;1] 3) Функция чет Свойства функции y=cosx 1) D(cosx): (-∞;+∞) 2) E(cosx): [-1;1] 3) Функция чет](https://fs01.infourok.ru/images/doc/58/72316/310/img7.jpg)
Описание слайда:
Свойства функции y=cosx 1) D(cosx): (-∞;+∞) 2) E(cosx): [-1;1] 3) Функция четная: cos(-x)=cosx. График функции симметричен оси y. 4) Периодическая: Т = 2П cosx = cos (x+2П)
9 слайд

Описание слайда:
Свойства функции y=cosx 5) Точки пересечения с осью х: (П/2+Пn;0) nЄZ 6) Точки пересечения с осью у: (0;1) 7) Промежутки знакопостоянства: cosx>0:(-П/2+2Пn;П/2+2Пn) nЄZ cosx<0:(П/2+2Пn;3П/2+2Пn)nЄZ
10 слайд
![Свойства функции y=cosx 8) Промежутки монотонности: [-П+2Пn;2Пn], nЄZ [2Пn;П+ Свойства функции y=cosx 8) Промежутки монотонности: [-П+2Пn;2Пn], nЄZ [2Пn;П+](https://fs01.infourok.ru/images/doc/58/72316/310/img9.jpg)
Описание слайда:
Свойства функции y=cosx 8) Промежутки монотонности: [-П+2Пn;2Пn], nЄZ [2Пn;П+2Пn], nЄZ 9) Точки экстремума: x min =-П+2Пn; 10) Экстремумы функции: y min =-1; y max = 1 x max = 2Пn
11 слайд

Описание слайда:
Преобразования графика y=cosx
12 слайд

Описание слайда:
y = – cos x график функции у =cos x отобразить симметрично относительно оси х
13 слайд

Описание слайда:
у=Acos x график функции y=cos x 1) растянуть вдоль оси у, если /А/>1; 2) сжать вдоль оси у, если /А/<1. все значения у уменьшаются в 2 раза все значения у увеличиваются в 2 раза
14 слайд

Описание слайда:
у= cos (x+a) ось у сдвинуть на а ед.отрезков вправо y= cos (x+2n/3) y= cos (x-a) ось у сдвинуть на а ед.отрезков влево y= cos (x-2n/3)
15 слайд

Описание слайда:
y = cos (x)+b ось х сдвинуть на b ед.отрезков вниз сдвинуть ось х на 2 ед. отр. вниз y = cos (x)-b ось х сдвинуть на b ед.отрезков вверх y=cos (x)-2 сдвинуть ось х на 2 ед. отр. вверх
16 слайд

Описание слайда:
y = cos (аx) сжать вдоль оси х, если a>1 растянуть вдоль оси х, если a<1 y = cos (2x) период: T=2П/2=П сжать вдоль оси х в 2 раза период:T=2П/0,5=4П растянуть вдоль оси х в 2 раза y = cos (0,5x)
Выберите книгу со скидкой:
БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА
Инфолавка – книжный магазин для педагогов и родителей от проекта «Инфоурок»

Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики и информатики

Курс профессиональной переподготовки
Учитель математики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Номер материала:
186000092745
Вам будут интересны эти курсы:
Оставьте свой комментарий
Источник
Алгебра и начала математического анализа, 11 класс
Урок №3. Свойства и график функции y=cos x
Перечень вопросов, рассматриваемых в теме
Глоссарий по теме
Амплиту́да — максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении.
Функция y=f(x) возрастает на интервале X, если для любых  и
и  ,
,  выполняется неравенство
выполняется неравенство  . Другими словами – большему значению аргумента соответствует большее значение функции.
. Другими словами – большему значению аргумента соответствует большее значение функции.
Функция y=f(x) убывает на интервале X, если для любых  и
и  ,
,  выполняется неравенство
выполняется неравенство  . Другими словами – большему значению аргумента соответствует меньшее значение функции.
. Другими словами – большему значению аргумента соответствует меньшее значение функции.
Точку х0 называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство  . Значение функции в точке максимума называют максимумом функции и обозначают ymax.
. Значение функции в точке максимума называют максимумом функции и обозначают ymax.
Точку х0 называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство  . Значение функции в точке минимума называют минимумом функции и обозначают ymin.
. Значение функции в точке минимума называют минимумом функции и обозначают ymin.
Основная литература:
Колягин М.В. Ткачева Ю.М., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: https://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс]. – Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Напомним, что все тригонометрические функции являются периодическими функциями. Функции  и
и  повторяются через каждые 360° (или 2π радиан), поэтому 360° называется периодом этих функций (рис.1).
повторяются через каждые 360° (или 2π радиан), поэтому 360° называется периодом этих функций (рис.1).

Рис. 1 – графики функций  и
и  .
.
Функции  и
и  повторяются через каждые 180° (или π радиан), поэтому 180° — это период для данных функций (рис. 2).
повторяются через каждые 180° (или π радиан), поэтому 180° — это период для данных функций (рис. 2).

Рис. 2 – графики функций  и
и  .
.
В общем случае если  и
и  (где
(где  — константа), то период функции равен
— константа), то период функции равен  (или
(или  радиан). Следовательно, если
радиан). Следовательно, если  , то период этой функции равен
, то период этой функции равен  , если
, если  , то период этой функции равен
, то период этой функции равен  .
.
Амплитудой называется максимальное значение синусоиды. Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1).

Рис. 3 – изображение амплитуды графиков  и
и  .
.
Однако, если  , каждая из величин
, каждая из величин  умножается на 4, таким образом, максимальная величина амплитуды — 4. Аналогично для
умножается на 4, таким образом, максимальная величина амплитуды — 4. Аналогично для  амплитуда равна 5, а период —
амплитуда равна 5, а период —  .
.

Рис. 4 – график функции  .
.
Свойства функции  :
:
- Область определения – множество R всех действительных чисел.
- Множество значений – отрезок [−1;1].
- Функция
 периодическая, Т=2π.
периодическая, Т=2π. - Функция
 – чётная
– чётная - Функция
 принимает:
принимает:
- Функция

Интересно, что графиками тригонометрических функций –косинус и синус описываются многие процессы в нашей жизни. Например, работа сердца. Сделанная электрокардиограмма (ЭКГ) представляет собой график синусоиды, отражающую биоэлектрическую активность сердца. Или еще пример, электромагнитные волны к ним относятся: мобильные телефоны, беспроводная связь, радио, СВЧ-печи тоже распространяются по закону синуса или косинуса. Их существование было предсказано английским физиком Дж.Максвеллом в 1864 году.
Актуализация знаний
Напомним, что множество значений функции y=cosx принадлежит отрезку [–1;1], определена данная функция на всей числовой прямой и, следовательно, функция ограничена и график её расположен в полосе между прямыми y=–1 и y=1.
Так как функция периодическая с периодом  , то достаточно построить её график на каком-нибудь промежутке длиной
, то достаточно построить её график на каком-нибудь промежутке длиной  , например на отрезке
, например на отрезке  Тогда на промежутках, полученных сдвигами выбранного отрезка на
Тогда на промежутках, полученных сдвигами выбранного отрезка на  , график будет таким же.
, график будет таким же.
Функция  является чётной. Поэтому её график симметричен относительно оси Оу. Для построения графика на отрезке
является чётной. Поэтому её график симметричен относительно оси Оу. Для построения графика на отрезке  достаточно построить для
достаточно построить для  а затем симметрично отразить его относительно оси Оу (рис. 5)
а затем симметрично отразить его относительно оси Оу (рис. 5)

Рис. 5 – график функции  .
.
Примеры и разборы решения заданий тренировочного модуля:
Пример 1. Найдем все корни уравнения  , принадлежащие отрезку
, принадлежащие отрезку  .
.
Построим графики функций  и
и  (рис. 6)
(рис. 6)

Рис. 6 – графики функций  и
и  .
.
Графики пересекаются в трёх точках, абсциссы которых  являются корнями уравнения
являются корнями уравнения  . На отрезке от
. На отрезке от  корнем уравнения является число
корнем уравнения является число  . Из рисунка видно, что точки х1 и х2 симметричны относительно оси Оу, следовательно
. Из рисунка видно, что точки х1 и х2 симметричны относительно оси Оу, следовательно  . А
. А  .
.
Пример 2.Найти все решения неравенства  , принадлежащие отрезку
, принадлежащие отрезку  .
.
Из рисунка 6 видно, что график функции  лежит ниже графика функции
лежит ниже графика функции  на промежутках
на промежутках  и
и 
Ответ:  ,
,  .
.
Источник
Теория
| 1. | Свойства функции y = cosx и её график |
Задания
| 1. | Возрастание и убывание функции y = cosx Сложность: | 1 |
| 2. | Сравнение чисел с использованием свойств функции y = cosx Сложность: | 2 |
| 3. | Определение значений косинусов некоторых углов Сложность: | 1 |
| 4. | Преобразование выражения cos t и определение его значения Сложность: | 1 |
| 5. | Применение формул приведения к сравнению чисел Сложность: | 2 |
| 6. | Построение графика функции y = cosx + b или y = cos(x + а) Сложность: | 1 |
| 7. | Принадлежность точек графику функции y = k cos(x + a) + b Сложность: | 1 |
| 8. | Нахождение наибольшего и наименьшего значений функции y = cosx Сложность: | 1 |
| 9. | Область значений функции y = cosx Сложность: | 1 |
| 10. | Определение чётности функции Сложность: | 1 |
| 11. | Решение уравнения cosx = ax + b графически Сложность: | 1 |
| 12. | Определение наибольшего и наименьшего значений функции Сложность: | 2 |
| 13. | Построение графиков функций y = cos(x + a) + b Сложность: | 4 |
Тесты
| 1. | Тренировка по теме Функции y = cosx Сложность: лёгкое | 4 |
Методические материалы
| 1. | Технологическая карта |
Источник
Комментарии преподавателя
Функция y=cost, её свойства, график и типовые задачи
1. Тема урока, введение
На прошлом уроке мы построили график функции, осуществив сдвиг кривой на влево, и рассмотрели свойства функции Сейчас мы детализируем эти свойства и применим их к решению важнейших типовых задач.
2. Поведение и особенности функции y=cost на промежутке [0; π]
Рассмотрим поведение функции и отметим важнейшие точки на промежутке
В координатной плоскости (рис. 1).
На числовой окружности (рис. 2).
Сформулируем основные особенности функции при
1. Функция монотонно убывает от до
2. Функция принимает все значения из отрезка
3. Каждое свое значение функция принимает при единственном значении аргумента (следует из монотонности функции).
3. Решение задач
Задача 1. Найти пределы изменения функции на данном отрезке.
1)
Рис. 3.
На заданном отрезке функция монотонно убывает, значит, наименьшее значение принимает на правом конце.
Ответ:
2)
Рис. 4.
Функция монотонно убывает.
Ответ:
3)
Рис. 5.
На данном промежутке функция немонотонна.
Ответ:
Монотонность функции означает, что не только каждому значению аргумента соответствует единственное значение функции, но и обратное – каждое значение функции достигается при единственном значении аргумента.
Например:
Если единственное решение на промежутке
Если
Сколько решений имеет уравнение на промежутке Одно, также в силу монотонности.
Задача 2. Найти все значения параметра при каждом из которых уравнение имеет хотя бы одно решение:
1)
2)
Решение:
1) Построим график функции (рис. 6).
Уравнение имеет хотя бы одно решение при
В данном случае множество значений параметра совпадает со множеством значений функции.
Ответ:
2) Решим другим способом, используя область значений функции
Ответ:
Задача 3. Решить уравнение
Решение:
Построим в одних координатных осях графики функций (рис. 7).
Графики имеют только одну общую точку
Решим уравнение еще одним способом.
Ответ:
Задача 4. Найти число корней уравнения
Решение (рис. 8).
На промежутке функция монотонно возрастает, функция монотонно убывает. Это значит, что на данном промежутке графики имеют только одну общую точку.
На промежутке функция убывает, функция возрастает, значит, и на этом промежутке графики также имеют только одну общую точку.
Ответ: Два корня.
4. Вывод, заключение
Мы рассмотрели и детализировали свойства функции и использовали их при решении задач. В дальнейшем рассмотренные свойства будут неоднократно использоваться.
ИСТОЧНИК
https://interneturok.ru/ru/school/algebra/10-klass/trigonometricheskie-funkcii/funktsiya-y-cos-t-eyo-svoystva-grafik-i-tipovye-zadachi
https://www.youtube.com/watch?v=RAib0ZZBTEg
https://www.youtube.com/watch?v=BTcC6Gw3T1U
https://11book.ru/images/shcoolbook_ru/10/10_a_mord_baz.pdf
https://vklasse.org/10-klass/reshebniki/algebra/ag-mordkovich-2009-zadachnik/glava-2-trigonometricheskie-funktsii/11-funktsiya-ucos-x-ee-svojstva-i-grafik/13
https://www.yaklass.ru/p/algebra/10-klass/trigonometricheskie-funktcii-10781/svoistva-funktcii-y-cosx-i-ee-grafik-10783/re-25f9a2dd-12ec-4034-b283-f0a0973c4f52
https://rpp.nashaucheba.ru/pars_docs/refs/47/46657/img7.jpg
Источник
Презентация на тему: Функция y=cos x
Скачать эту презентацию
Скачать эту презентацию
№ слайда 1

Описание слайда:
Наумова Ирина Михайловна * Функция y = cos x Ее свойства и график 900igr.net Наумова Ирина Михайловна
№ слайда 2

Описание слайда:
Наумова Ирина Михайловна * Сегодня мы рассмотрим Построение графика функции y = cos x; Свойства функции y = cos x; Изменение графика функции y = cos x в зависимости от изменения функции и аргумента; Изменение свойств функции y = cos x в зависимости от изменения функции и аргумента; Примеры построения графиков функций путем анализа изменения их свойств. Наумова Ирина Михайловна
№ слайда 3

Описание слайда:
Наумова Ирина Михайловна * Построение графика Функция y = cos x определена на всей числовой прямой и множеством ее значений является отрезок -1; 1 . Следовательно, график этой функции расположен в полосе между прямыми у = -1 и у = 1. Наумова Ирина Михайловна
№ слайда 4

Описание слайда:
Наумова Ирина Михайловна * Как использовать периодичность и четность при построении Так как функция периодическая с периодом 2 , то достаточно построить ее график на каком – нибудь промежутке длиной 2 , например на отрезке – х ; тогда на промежутках, получаемых сдвигами выбранного отрезка на 2 n, n Z, график будет таким – же. Функция y = cos x является четной. Поэтому ее график симметричен относительно оси OY. Для построения графика на отрезке – х достаточно построить его для 0 х , а затем симметрично отразить относительно оси OY. Наумова Ирина Михайловна
№ слайда 5
Описание слайда:
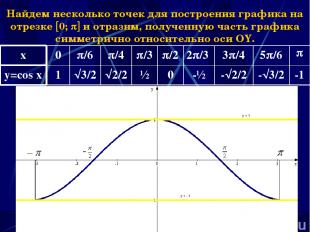
Наумова Ирина Михайловна * Найдем несколько точек для построения графика на отрезке 0; и отразим, полученную часть графика симметрично относительно оси OY. x 0 /6 /4 /3 /2 2 /3 3 /4 5 /6 y=cos x 1 3/2 2/2 ½ 0 -½ – 2/2 – 3/2 -1 Наумова Ирина Михайловна
№ слайда 6
Описание слайда:
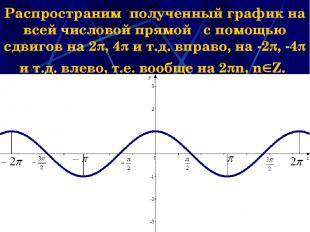
Наумова Ирина Михайловна * Распространим полученный график на всей числовой прямой с помощью сдвигов на 2 , 4 и т.д. вправо, на -2 , -4 и т.д. влево, т.е. вообще на 2 n, n Z. Наумова Ирина Михайловна
№ слайда 7

Описание слайда:
Наумова Ирина Михайловна * Итак, график функции y = cos x построен геометрически на всей числовой прямой, начиная с построения его части на отрезке 0; . Поэтому свойства функции y = cos x можно получить , опираясь на свойства этой функции на отрезке 0; . Например, функция y = cos x возрастает на отрезке – ; 0 , так как она убывает на отрезке 0; и является четной. Перечислим основные свойства функции y = cos x. Наумова Ирина Михайловна
№ слайда 8

Описание слайда:
Наумова Ирина Михайловна * Для этого нужно вспомнить Как найти область определения и множество значений тригонометрических функций; Какие функции называются периодическими и как найти период функции; Какие функции называются четными (нечетными); Когда функция возрастает (убывает); Как найти нули функции; Как определить на каких промежутках функция принимает положительные (отрицательные) значения; Как определить когда функция принимает наибольшее (наименьшее) значения. Наумова Ирина Михайловна
№ слайда 9

Описание слайда:
Наумова Ирина Михайловна * Область определения Каждому действительному числу х соответствует единственная точка единичной окружности, получаемая поворотом точки 1; 0 на угол х радиан. Для этого угла определены sin x и cos x. ?

