Какое число молекул содержится в водороде объемом 5 м3
Молекулы вступают в реакцию в определённых соотношениях, и это описывают химические реакции. Например, из этого уравнения
2Н2 + О2 = 2Н2О
видно, что в реакции приняли участие 2 молекулы водорода и 1 молекула кислорода, образовав при этом 2 молекулы воды. Но молекула так малы, что увидеть их невозможно, и уж тем более нельзя взять их в руки. Поэтому в учебнике химии и появляется понятие моль – количество вещества, в котором содержится число Авогадро частиц (6,02*10 в двадцать третьей степени). Рядом с этим понятием стоит другое – молярная масса, то есть масса 1 моля частиц. Молярная масса совпадает с атомной или молекулярной, рассчитывается по таблице Менделеева и выражается в граммах на моль (г/моль).
Фото: pixabay.com
Но мы прекрасно знаем, что не все вещества в обычных условиях находятся в твёрдом или жидком состоянии. Например, кислород, азот, хлор, неон – это газы. Резонно спросить: а как же их взвешивать? На этот случай химии для 8 класса припасено ещё одно понятие – молярный объём.
Что такое молярный объём
Тут следует запомнить, что в обычных условиях 1 моль любого газа занимает одинаковый объём. То есть молярный объём – это объём 1 моля любого газа. Сейчас советую на всякий случай вспомнить, что в 1 моле любого вещества (в том числе газа) содержится число Авогадро частиц. Старайтесь не забывать об этом факте.
Теперь надо обязательно упомянуть следующее. Все знают, что при изменении температуры и давления объём газов меняется. Так вот чтобы все расчёты вести правильно, то есть в одинаковых условиях, говорят о нормальных условиях: температуре 0 градусов Цельсия и давлении в 1 атмосферу (или 101,3 кПа). Это нужно просто запомнить:
нормальные условия в химии: температура – 0 градусов Цельсия, давление – 1 атм.
Экспериментально было доказано, что в нормальные условиях 1 моль любого газа занимает объем 22,4 литра.
То есть молярный объём любого газа в н.у. составляет 22,4 л/моль.
И это число тоже нужно запомнить! Оно даже важнее, чем сами нормальные условия, потому используется это число в решениях по химии намного чаще, чем н.у. (нормальные условия).
Как найти молярный объём
Очень просто. Если молярную массу для каждого вещества нужно рассчитывать по таблице Менделеева, то
молярный объём для всех газов одинаков.
Пример 1.
Молярная масса воды Н2О 18 г/моль (2*1+16, всё берем из периодической таблицы), молярная масса оксида кальция СаО 56 г/моль (40+16), молярная масса серной кислоты Н2SO4 98 г/моль (2*1+32+4*16).
Зато в нормальных условиях молярный объём кислорода О2 22,4 л/моль, молярный объём фтора P2 22,4 л/моль, молярный объём ксенона 22,4 г/моль. Приятно, не правда ли?
Другое дело, если речь идёт о химических реакциях. Но для начала просто потренируемся с цифрами.
Пример 2.
Определите объём, который занимают 10 моль кислорода в н.у.
Решение:
Молярный объём кислорода 22,4 л/моль, то есть 1 моль занимает 22,4 л. Следовательно, 10 моль будут занимать в 10 раз больше 22,4*10=224 литра. Это и есть ответ: 10 моль кислорода займут объём 224 литра.
Пример 3.
Известно, что неон в н.у. занял объём 5,6 литра. В каком количестве взят неон (в молях)?
Решение:
1 моль занимает объём 22,4 литра, а вот неизвестное число моль заняло объём 5,6 литра. Можно составить пропорцию:
1 моль – 22,4 литра
Х моль – 5,6 литра
Отсюда Х=1*5,6/22,4=0,25. Значит ответ такой: неон взяли в количестве 0,25 моль.
Пример 4.
Это уже расчёт по химической реакции, поэтому будьте внимательны. Итак, хлор прореагировал с водородом с образованием хлорида водорода:
Н2 + Cl2 = 2HCl
Для реакции взяли 11,2 литра водорода. Сколько понадобилось хлора (н.у.)?
Решение:
Посмотрим, сколько нам дано водорода по условию задачи. 1 моль водорода занимает объём 22,4 литра. Но у нас всего 11,2 литра водорода, то есть Х моль. Составим пропорцию:
1 моль – 22,4 литра
Х моль – 11,2 литра
Отсюда Х=1*11,2/22,4=0,5 моль водорода. Значит, по условию задачи у нас водорода 0,5 моль.
Из уравнения химической реакции Н2 + Cl2 = 2HCl видно, что нам нужно по 1 молю водорода и хлора (об этом говорят коэффициенты в уравнении). То есть, 1 моль водорода реагирует с 1 молем хлора. Но нам дали всего 0,5 моль водорода, сколько нам нужно хлора? Составим ещё одну пропорцию:
1 моль водорода реагирует с 1 молем хлора
0,5 моль водорода реагирует с Х молями хлора.
Отсюда получаем: Х=0,5*1/1=0,5 моль. Таким образом, нам нужно 0,5 моль хлора. А это количество занимает объём 22,4*0,5=11,2 литра.
Ответ: понадобилось 11,2 литра хлора.
В следующий раз мы научимся делать расчёты по реакциям, в которых участвуют и твёрдые вещества, и газы, то есть одновременно будем использовать молярную массу и молярный объём.
Пишите, пожалуйста, в комментариях, что осталось непонятным, и я обязательно дам дополнительные пояснения. Жалуйтесь на сложности в изучении школьного курса и говорите, что вас испугало в учебнике химии. И тогда следующая статья будет рассказывать именно об этой проблеме.
Источник
Задача 53.
Сопоставить числа молекул, содержащихся в 1г NH3 и в 1г N2. В каком случае и во сколько раз число молекул больше?
Решение:
В одном моле любого вещества содержится 6,02 . 1023 молекул этого вещества.
Рассчитаем содержание количества вещества в 1г NH3 и N2 по формуле:
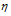(B) – количество вещества (В);
m(B)- масса вещества (В);
M(B) – Молярная масса вещества (В).
М(NH3) = 17г/моль, M(N2) = 28г/моль.
Тогда
Число молекул NH3 больше числа молекул N2, так как 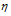(NH3) >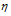(N2) . Теперь рассчитаем, во сколько раз число молекул NH3 больше числа молекул N2:
Ответ: в 1,65 раз число молекул NH3 больше числа молекул N2.
Задача 54.
Выразить в граммах массу одной молекулы диоксида серы.
Решение:
Находим молекулярную массу диоксида серы:
M(SO2) = 32 + (16 . 2) = 64г/моль.
Молекулярная масса численно составляет массу одного моля вещества, а значит, вес одного моля численно равен молекулярной массе и составляет 64г. Известно, что в одном моле любого вещества содержится 6,02 . 1023 молекул данного вещества. Исходя из этого, рассчитаем массу в граммах одной молекулы диоксида серы:
Ответ: масса одной молекулы диоксида серы равна.
Задача 55.
Одинаково ли число молекул в 0,001кг Н2 и в 0,001кг О2? В 1 моле Н2 и в 1 моле 02? В 1л Н2 и в 1л О2 при одинаковых условиях?
Решение:
Молекулярные массы водорода и кислорода равны соответственно 2г/моль и 32г/моль. Отсюда находим количество водорода и кислорода, зная их массы:
Один моль любого вещества содержит 6,02 .1023 молекул. Следовательно, в 0,001кг водорода и в 0,001кг кислорода содержится разное число молекул:
Так как имеется по одному молю водорода и кислорода, то количество молекул веществ будет одинаково:
Согласно закону Авогадро в равных объёмах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул, Один моль любого газа занимает 22,4л, В которых содержится 6,02 . 1023 молекул. Отсюда рассчитаем количество молекул вещества, содержащихся в 1л водорода и в 1л кислорода:
Ответ: а) в 0,001кг водорода и в 0,001кг кислорода содержится разное число молекул; б) в одном моле водорода и в одном моле кислорода содержится одинаковое число молекул: в) в одном литре водорода и в одном литре кислорода содержится одинаковое число молекул.
Задача 56.
Сколько молекул содержится в 1,00 мл водорода при нормальных условиях?
Решение:
Согласно закону Авогадро в равных объёмах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул, Один моль любого газа занимает 22,4л, В которых содержится 6,02 .1023 молекул. Отсюда рассчитаем количество молекул вещества, содержащихся в 1мл водорода из пропорции:
Ответ: 2,69 .1019 молекул.
Задача 57.
Какой объем при нормальных условиях занимают 27 .1021 молекул газа?
Решение:
Согласно закону Авогадро в равных объёмах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул, Один моль любого газа занимает 22,4л, В которых содержится 6,02 . 1023 молекул. Отсюда находим какой объём при нормальных условиях занимают 27 .1021 молекул газа, составив пропорцию:
Ответ: V=1л.
Задача 58.
Каково соотношение объемов, занимаемых 1 молем О2 и 1 молем О3 (условия одинаковые)?
Решение:
Согласно закону Авогадро в равных объёмах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул, Один моль любого газа занимает 22,4л. Следовательно соотношение объёмов, занимаемых одним молем О2 и одним молем О3 иметь вид:
Ответ: 1:1
Задача 59.
Взяты равные массы кислорода, водорода и метана при одинаковых условиях. Найти отношение объемов взятых газов.
Решение:
Согласно закону Авогадро в равных объёмах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул, Один моль любого газа занимает 22,4л. Мольные массы кислорода, водорода и метана, соответственно равны 32 г/моль; 2г/моль; 16 г/моль.
Так как массы кислорода, водорода и метана одинаковы при одинаковых условиях, то отношение объёмов взятых газов находим из пропорции:
Ответ: 1:16:2.
Задача 60.
На вопрос, какой объем займет 1моль воды при нормальных условиях, получен ответ: 22,4л. Правильный ли это ответ?
Решение:
Согласно закону Авогадро в равных объёмах любых газов, взятых при одинаковых условиях, содержится одинаковое число молекул, Один моль любого газа занимает 22,4л. Так как вода при нормальных условиях находится в жидкой, а не в газообразной фазе, то ответ, что 1моль воды займёт 22,4л не правильный. Учитывая, что молярная масса воды равна 18г/моль, а плотность равна единице, то правильный ответ будет равен:
Ответ: 18мл.
Задача 61.
Сколько молекул диоксида углерода находится в 1л воздуха, если объемное содержание СО2 составляет 0,03% (условия нормальные)?
Решение:
При нормальных условиях углекислый газ, содержащийся в 1л воздуха, занимает объём 0,0003л. Зная, что мольный объём любого газа занимает 22,4л, рассчитаем число молей углекислого газа в 0,0003л из пропорции:
Учитывая, что в одном моле вещества содержится 6,02 . 1023 молекул, находим число молекул в 0,0003л газа:
Ответ: 8,07 .1018 молекул.
Источник
Примеры решения задач
1. Молекулярно-кинетическая теория
идеальных газов
Задача 1. Определить, сколько киломолей и молекул водорода содержится в объеме 50 м3 под давлением 767 мм рт. ст. при температуре 18°С.
Какова плотность и удельный объем газа?
Дано: V = 50 м3 Ρ = 767 Т = 291 К М = 2 кг/моль | Решение: На основании уравнения Менделеева устанавливаем число киломолей ν, содержащихся |
ν – ? N – ? ρ – ? d – ? |
можно определить ν:
Число молекул N, содержащихся в данном объеме,
находим, используя число Авогадро NА (которое определяет какое количество молекул
содержится в одном киломоле). Общее количество молекул, находящихся в массе m
данного газа, может быть установлено, так как известно число молей ν.
Подставляя в формулу число киломолей, устанавливаем
число молекул, содержащихся в объеме V: .
Плотность газа ρ = m/V определяем
из уравнения Менделеева – Клайперона:
Подставляя числовые значения в единицах СИ в формулу,
определим плотность газа:
Удельный объем газа d определяем из уравнения
Менделеева – Клайперона:
Ответ: 11,9 м3/кг.
Задача 2. В сосуде объемом
2 м3 находится смесь 4 кг гелия и 2 кг водорода при температуре 27°С.
Определить давление и молярную массу смеси газов.
Дано: V = 2 м3 m1= 4 кг М1= 4·10-3 кг/кмоль m2= 2 кг М2= 2·10-3 кг/кмоль Т1= 300 К | Решение: Воспользуемся уравнением Менделеева (1) (2) где р1 – парциальное давление гелия; m1 |
р – ? М – ? |
М1
– его молярная масса; V – объем сосуда; Т – температура газа; R = 8,31 Дж/(моль·К)
–молярная газовая постоянная; р2 – парциальное давление водорода; m2 – масса водорода;
М2 – его молярная масса.
По закону Дальтона: (3)
Из уравнений (1) и (2) выразим р1 и р2 и подставим
в уравнение (3):
(4)
С другой стороны, уравнение Менделеева – Клайперона
для смеси газов имеет вид:
(5)
Сравнивая (4) и (5) найдем молярную массу
смеси газов по формуле:
, (6)
где ν1 и ν2 – число молей гелия
и водорода соответственно.
Ответ: 3·10-3 кг/моль.
Энтропия в замкнутых системах. Обратимость процессов как условие сохранения
энтропии. Энтропия и необратимость. Неравенство Клаузиуса
Для пояснения связи энтропии с неполной превращаемостью теплоты в работу
обратимся снова к циклу Карно, используя целесообразную в данном случае дифференциальную
форму записи. Поскольку никаких потерь в машине Карно нет, то полученную за
цикл от машины работу можно представить как разность теплоты, полученной рабочим
телом (идеальным газом) от нагревателя, и теплоты, отданной рабочим телом
холодильнику, то есть dA = dQн – dQх. Теперь воспользуемся выражением для
коэффициента полезного действия машины Карно (4.1) dAdQн
= 1 – dQх /dQн =1 – Тх /Тн. Откуда dQх /dQн = Тх /Тн . При передаче теплоты
рабочему телу в изотермическом процессе равны температуры Тн = Трт нагревателя
и рабочего тела и, соответственно, равны отданная нагревателем теплота и теплота,
полученная рабочим телом, dQн = dQрт. Теперь, используя выражение (5.1) для
изменения энтропии, мы можем представить принципиально не преобразуемую в
работу за цикл часть взятой у нагревателя теплоты выражением dQх = Тх (dQн
/ Тн) = Тх (dQрт / Трт ) = ТхdS ,
из которого видно, что количество принципиально не преобразуемой в работу
за цикл теплоты зависит от температуры холодильника тепловой машины и изменения
в рабочем цикле энтропии рабочего тела, а именно равно их произведению. Здесь
речь идет о том количестве энтропии, которое забирается рабочим телом у нагревателя
и отдается холодильнику, и при этом понижается степень хаотичности состояния
нагревателя, но в равной мере повышается степень хаотичности холодильника,
а в целом хаотичность состояния всей системы остается неизменной. Поскольку
каждый из сомножителей в правой части равенства в замкнутой системе не может
быть равен нулю, то невозможно за цикл не отдавать часть теплоты холодильнику
(утрачивая после этого возможность ее дальнейшего преобразования в работу).
Уравнение (5.1) показывает, что в теплоизолированной термодинамической системе
энтропия может сохраняться, но это условие (отсутствие теплообмена с внешним
миром) является лишь необходимым, но не достаточным условием для сохранения
энтропии.
Опыт показывает, что в изолированных системах даже при отсутствии теплообмена
энтропия может возрастать, если в них идут релаксационные процессы самопроизвольного
выравнивания термодинамических параметров. Для возвращения системы в первоначальное
состояние теперь необходимо внешнее воздействие – систему можно квазистатическим
образом перевести в начальное состояние, используя отвод теплоты и вычисляя
необходимое уменьшение энтропии согласно уравнению (5.1).
Спонтанные (самопроизвольные) изменения в теплоизолированной (адиабатически
замкнутой) системе всегда ведут к возрастанию энтропии. В этой асимметрии
течения природных процессов заключена причина различимости прошлого и будущего.
С течением релаксационных процессов в системе постепенно утрачивается возможность
преобразования теплоты в работу, которая раньше существовала в силу наличия
перепадов (неравномерности по объему) интенсивных параметров, например, при
выравнивании температур нагревателя и холодильника у тепловой машины. Происходит
также так называемая диссипация (рассеяние) энергии за счет работы сил трения,
то есть превращение энергии макроскопических движений тел в энергию хаотического
движения микрочастиц. Это означает, что самопроизвольно степень хаотичности
состояния системы может только увеличиваться, но никогда не убывает, оставаясь
неизменной в замкнутых системах лишь в случае протекания в них полностью обратимых
процессов.
Источник
Решение задач на количественные характеристики вещества:
количества вещества, массу и объем
Количество вещества (ν) связано с числом структурных единиц (N) в образце вещества, его массой (m) и объемом (V) — для газообразных веществ при н. у. — следующими уравнениями:
в которых
Vm = 22,4 л/моль (мл/ммоль, м3/кмоль) при н.у.,
NA = 6,02 • 1023 (постоянная Авогадро),
а молярная масса (М) численно равна относительной молекулярной массе вещества.
Цитаты из пособия «Задачи по химии 8-9 кл.» (авт. О.С. Габриелян и др.) использованы в учебных целях. Ссылка на покупку книги указана в конце конспекта.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
№ 1.
Определите абсолютную массу (в г) одной молекулы воды.
Ответ: m (молекулы Н2O) = 2,99 • 10–23 г.
№ 2.
Определите массу порции оксида серы (VI), содержащей 7,224 • 1023 атомов кислорода.
Ответ: m(SO3) = 32 г.
№ 3.
Сколько атомов азота содержится в оксиде азота (I), объем которого (н. у.) равен 20,16 л?
Ответ. N(N) = 10,836 • 1023.
№ 4.
Определите объем (н. у.) оксида углерода (IV), в котором содержится столько же атомов кислорода, сколько их содержится в 48 г карбоната кальция.
Ответ. V(СO2) = 16,12 л.
№ 5.
Определите относительную плотность сероводорода по водороду и по воздуху.
Ответ: DH2(H2S) = 17; Dвозд(H2S) = 1,17.
№ 6.
Плотность газа по кислороду равна 0,875. Определите число молекул, содержащихся в 15,4 г этого газа.
Ответ. N(газа) = 3,311 • 1023.
ЗАДАЧИ с КРАТКИМ ОТВЕТОМ
№ 7. Сплав содержит 16 г меди и 11,2 г железа. Атомов какого метала будет больше в данном образце сплава?
№ 8. Смешали 16,8 г азота и 15,68 л (н. у.) водорода. Какое суммарное число молекул обоих газов будет содержаться в данной смеси?
№ 9. Чему равна масса порции хлорида бария, содержащая 1,3244 • 1024 ионов хлора?
№ 10. Какую массу должен иметь образец нитрата калия, чтобы в нем было столько же атомов кислорода, сколько их содержится в образце сульфата натрия массой 21,3 г?
№ 11. Сколько атомов хлора содержится в смеси, состоящей из 16,68 г хлорида фосфора (V) и 16,5 г хлорида фосфора (III)?
№ 12. Вычислите массу смеси, содержащей 672 мл (н. у.) оксида азота (I), 0,125 моль оксида азота (II) и 1,15 г оксида азота (IV). Сколько атомов азота будет содержаться в этой смеси?
№ 13. Молекула некоторого газа имеет массу 6,063* 10–23г. Определите плотность данного газа по гелию.
№ 14. Вычислите плотность газа по азоту, если 1 л (н. у.) этого газа имеет массу 1,7857 г.
№ 15. Плотность газа по воздуху равна 2,207. Найдите плотность этого газа по хлору и массу одной молекулы этого газа (в г).
№ 16. Масса порции оксида алюминия равна массе порции оксида кремния (IV). В какой порции будет содержаться больше атомов кислорода?
№ 17. Порции метана СН4 и аммиака NH3 содержат одинаковое число атомов водорода. Какая порция будет иметь большую массу?
№ 18. Десять молекул газа имеют массу 6,063 * 10–22г. Определите плотность данного газа по водороду.
№ 19. Определите массу и объем (н. у.) аммиака, содержащего столько же атомов водорода, сколько их содержится в 2,55 г сероводорода.
Решение задач на основные количественные характеристики вещества. Выберите дальнейшие действия:
- Перейти к следующей теме: Решение задач с долей вещества в смеси, в соединении.
- Вернуться к списку конспектов по Химии.
- Проверить знания по Химии.
- Купить книгу Задачи по химии и способы их решения. 8-9 кл. / О.С. Габриелян и др. — М.: Дрофа.
Источник