Какое число молекул двухатомного газа содержится в сосуде объемом 20 см3

IV. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
7.ЗАКОНЫ ИДЕАЛЬНЫХ ГАЗОВ.
МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ
Основные формулы
1. Количество вещества
ν m , или ν N ,
NA
где N – число структурных элементов системы (молекул, атомов, ионов и т. д.); NA – постоянная Авогадро; – молекулярная масса.
2. Уравнение состояния идеальных газов (уравнение Менделеева– Клапейрона)
pV m RT ,
где т – масса газа; – молярная масса газа; R – универсальная газовая постоянная; Т – термодинамическая температура.
3. Закон Дальтона
p p1 p2 … pn,
где р – давление смеси газов; рi – парциальное давление i-го компонента смеси;
п – число компонентов смеси. 4. Молярная масса смеси газов
cм m1 m2 … mn . ν1 ν2 … νn
5. Концентрация частиц (молекул, атомов и т.п.) однородной системы
n NV NA .
где V – объем системы; – плотность вещества.
6. В МКТ пользуются физической (идеализированной) моделью, называемой идеальным газом, согласно которой:
а) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда.
б) пренебрегают силами взаимодействия между молекулами. Следовательно, потенциальная энергия взаимодействия молекул принимается равной нулю, а внутренняя энергия идеально газа – равной средней кинетической энергии молекул.
в) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
68

Заметим, что понятие идеального газа не применимо при очень низких температурах (близких к температуре конденсации данного газа) и при очень высоких давлениях.
Макропараметры газа р, V, T.
Основное уравнение МКТ идеального газа – уравнение, которое связывает макропараметры идеального газа с микропараметрами:
р | 1 | nm V 2 , | (3.1) | ||||||||||||||||||||||||||||||||
3 | ср | ||||||||||||||||||||||||||||||||||
где р – давление газа; m0 – масса молекулы газа m0 | ; n – число моле- | ||||||||||||||||||||||||||||||||||
кул газа в единице объема; Vср2 | NA | ||||||||||||||||||||||||||||||||||
– среднеквадратичная скорость молекул. | |||||||||||||||||||||||||||||||||||
р | 1 | nm V 2 | 2 | nm | Vср2 | 2 | n E | , | (3.2) | ||||||||||||||||||||||||||
2 | |||||||||||||||||||||||||||||||||||
3 | 0 ср | 3 | 3 | кин | |||||||||||||||||||||||||||||||
где Eкин | – средняя кинетическая энергия поступательного движения моле- | ||||||||||||||||||||||||||||||||||
кулы. | 3 | ||||||||||||||||||||||||||||||||||
Eкин | kT, | (3.3) | |||||||||||||||||||||||||||||||||
R | 2 | ||||||||||||||||||||||||||||||||||
где k | – постоянная Больцмана (k = 1,38 · 10–23 Дж/К). | ||||||||||||||||||||||||||||||||||
NA | |||||||||||||||||||||||||||||||||||
Основное управление МКТ можно записать в виде | |||||||||||||||||||||||||||||||||||
р nkT. | (3.4) | ||||||||||||||||||||||||||||||||||
Из уравнения (3.3) следует, что кинетическая энергия не зависит от ро- | |||||||||||||||||||||||||||||||||||
да вещества, а зависит только от температуры. | |||||||||||||||||||||||||||||||||||
7. Скорость молекул: средняя квадратичная | |||||||||||||||||||||||||||||||||||
vкв | , | или | vкв | ; | |||||||||||||||||||||||||||||||
3kT m1 | 3RT | ||||||||||||||||||||||||||||||||||
средняя арифметическая | |||||||||||||||||||||||||||||||||||
v | , | или | v | ; | |||||||||||||||||||||||||||||||
8kT m1 | 8RT | ||||||||||||||||||||||||||||||||||
наиболее вероятная | |||||||||||||||||||||||||||||||||||
v | , | или | v | 2RT | , | ||||||||||||||||||||||||||||||
в | 2kT m | в | |||||||||||||||||||||||||||||||||
1 | |||||||||||||||||||||||||||||||||||
где т1 – масса одной молекулы. | |||||||||||||||||||||||||||||||||||
69
Примеры решения задач
Задача 1. Сколько молекул содержится в 1 м3 водорода при нормальных условиях? Какова масса одной молекулы водорода?
Д а н о:
V = 1 м3
T = 273 ºК р = 1·105 Па
= 2·10–3 кг/моль
п0 = ? т = ?
Р е ш е н и е
Число молекул в одном моле любого газа (число Авогадро) NА = 6,02·1023 1/моль. Объем одного моля любого газа (в том числе и водорода) при нормальных условиях V0 = 22, 4 л/моль = 22,4·10–3 м3/моль.
Следовательно, число молекул водорода, содержащихся в 1 м3 при нормальных условиях, определяется соотношением
n0 NA 2,69 1025 1/моль.
V0
Эта величина одинакова для любого газа и называется числом Лошмидта. Масса одной молекулы водорода
NA
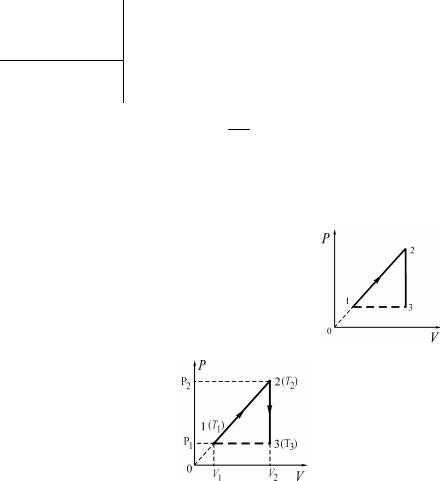
Задача 2. Моль одноатомного идеального газа участвует в процессе 1–2–3, представленном на p–V диаграмме.
Всостоянии 1 температура газа равна Т1 =
=100 ºК, а в состоянии 2 – Т2 = 400 ºК. Определите температуру газа Т3 в точке 3.
Т1 | Дано: | Решение |
= 100 ºК | ||
Т2 | = 400 ºК | V1 p1; |
Т3 = ? | ||
V2 p2. | ||
Запишем уравнение Менделеева–Клапейрона для состояний газа 1 и2:
pV RT ; | p2 RT ; | |||||
1 | 1 | 1 | 1 | 1 | ||
p2 RT | p2 | T | ||||
p V RT , | или | 1 | 1 | . | ||
p2 | ||||||
2 2 | 2 | 2 | 2 | T | ||
2 | 2 | |||||
70 | ||||||
Для изохорического процесса (2–3) можно записать:
p1 | T3 | ; | T1 | T3 | , следовательно, | ||
p2 | T2 | T2 | T2 | ||||
T3 T1 T2 200К.
Задача 3. Температур поверхностного слоя Солнца (фотосферы) – около 6000 ºК. Почему с поверхности Солнца не улетают атомы водорода, из которых в основном состоит фотосфера?
Р е ш е н и е
Средняя квадратичная скорость атомов водорода в фотосфере
Вторая космическая скорость
Как видно, средняя квадратичная скорость в 51 раз меньше второй космической скорости, поэтому большинство атомов водорода не могут вырваться из поля тяготения Солнца.
Задача 4. Определить плотность смеси 4 г водорода и 32 г кислорода при температуре 7 ºС и давлении 700 мм рт.ст.
Д а н о:
m1 = 4 г = 0,004 кг1 = 2·10–3 кг/моль m2 = 32 г = 0,032 кг
2 = 32·10–3 кг/моль T = 280 0К
рсм = 700 мм рт.ст. = = 700·133 = 9,31·104 Па
см = ?
отсюда
Р е ш е н и е
Чтобы найти плотность смеси, необходимо знать ее массу и объем, тогда
cм mсм ; mсм m1 m2 .
V
Объем смеси можно найти, используя уравнение Менделеева–Клапейрона:
p | см | p p | 2 | ; p V | m1 | RT; | p V | m2 | RT ; | |||||||
1 | 1 | 1 | 2 | 2 | ||||||||||||
m | m | 2 | RT | |||||||||||||
pсм | 1 | , | ||||||||||||||
V | ||||||||||||||||
2 | ||||||||||||||||
1 | ||||||||||||||||
71

m | m | ||||||||||
1 | 2 | ||||||||||
1 | 2 | RT | |||||||||
V | , | ||||||||||
и тогда | pсм | ||||||||||
4 10 3 | 32 10 3 9,31 104 | ||||||||||
m1 | m2 pсм | 3 | |||||||||
см | 0,48 кг/м . | ||||||||||
m | m | 2 | 4 10 | 3 | 32 10 | 3 | |||||
1 | RT | 8,31 280 | |||||||||
3 | 3 | ||||||||||
1 | 2 10 | 32 10 | |||||||||
2 | |||||||||||
Задача 5. На осях р-V изображены графически процессы, с помощью которых идеальный газ был переведен из состояния 1 в состояние 4. Начертить, как будут выглядеть эти же процессы 1-2, 2-3 и
3-4 на осях р-Т и V-Т, если 1-2 – изотерма. Расшифруем, графики каких процессов пока-
заны на осях:
1-2 – изотермическое сжатие;
2-3 – изобарическое сжатие;
3-4 – изохорический процесс с понижением давления.
Вычертим графики этих же процессов на других осях.
72
Задачи
7-1. В баллоне объемом 22,4 л находится водород при нормальных условиях. После того как в баллон было дополнительно введено некоторое количество гелия, давление в баллоне возросло до р2 = 0,25 МПа, а температура не изменилась. Определить массу гелия, введенного в баллон.
7-2. Смесь водорода и азота общей массой т = 290 г при температуре Т = 600 ºК и давлении р = 2,46 МПа занимает объем V = 30 л. Определить массу т1 водорода и массу т2 азота.
7-3. Оболочка воздушного шара имеет объем V = 1 600 м3. Найти подъемную силу FП водорода, наполняющего оболочку, на высоте, где давление р = 60 кПа и температура Т = 280 ºК. При подъеме шара водород может выходить через отверстиев нижней части.
7-4. Водород находится при температуре Т = 300 ºК. Найти среднюю кинетическую энергию вращательного движения одной молекулы, а также суммарную кинетическую энергию всех молекул этого газа; количество вещества водорода = 0,5 моль.
7-5. В баллоне объемом 10 л находится гелий под давлением р1 = 1 МПа при температуре Т1 = 300 ºК. После того как из баллона было взято 10 г гелия, температура в баллоне понизилась до Т2 = 290 ºК. Определить давление р2 гелия, оставшегося в баллоне.
7-6. Баллон содержит т1 = 80 г кислорода и т2 = 320 г аргона. Давление смеси р = 1 МПа, температура 300 ºК. Принимая данные газа за идеальные, определить объем баллона.
7-7. Какой объем занимает смесь азота массой т1 = 1 кг и гелия массой т2 = 1 кг при нормальных условиях?
7-8. В баллоне емкостью 15 л находится смесь, содержащая т1 = 10 г водорода, т2 = 54 г водяного пара и т3 = 60 г окиси углерода. Температура смеси 27 ºС. Определить давление.
7-9. Количество вещества гелия = 1,5 моль, температура Т = 120 ºК. Определить суммарную кинетическую энергию поступательного движения всех молекул этого газа.
7-10. Теплоизолированный сосуд объемом V = 2 м3 разделен пористой перегородкой на две равные части. Атомы гелия могут свободно проникать через поры в перегородке, а атомы аргона – нет. В начальный момент в одной части сосуда находится m = 1 кг гелия, а в другой – m = 1 кг аргона, а средняя квадратичная скорость атомов аргона игелия одинакова и составляет1000 м/с.
Определить температуру гелий-аргоновой смеси после установления равновесия в системе.
7-11. Найти плотность газовой смеси водорода и кислорода, если их массовые доли 1 и 2 равны соответственно 1/9 и 8/9. Давление смеси равно 100 кПа, температура Т = 300 ºК.
7-12. В сосуде объемом 2,24 л при нормальных условиях находится кислород. Определить количество вещества и массу т кислорода, а также концентрацию п0 его молекул в сосуде.
73
7-13. В сосуде находится смесь 10 г углекислого газа (СО2) и 15 г азота (N2). Найти плотность этой смеси при температуре 27 0С и давлении 1,5·105 Па.
7-14. Сосуд объемом 20 л содержит смесь водорода и гелия при температуре t = 20 ºС и давлении 2 атм. Масса смеси т = 5 г. Найти отношение массы водорода к массе гелия в данной смеси.
7-15. В баллон емкостью V = 12 л поместили т1 = 1,5 кг азота при температуре t1 = 327 ºС. Какое давление р2 будет создавать азот в баллоне при температуре t2 = 50 ºС, если 35 % азота будет выпущено. Каково было начальное дав-
ление р1?
7-16. На дне сосуда, заполненного воздухом, лежит полыйстальной шарик радиусом r = 2 см. Масса шарика 5 г. До какого давления р надо сжать воздух в сосуде, чтобы шарик поднялся вверх? Считать, что воздух при больших давлениях подчиняется уравнению газового состояния. Температура воздуха t = 20 ºС = = const (сжатие воздуха происходитдостаточно медленно).
7-17. На какой глубине радиус пузырька воздуха вдвое меньше, чем у поверхности воды, если давление у поверхности равно р0?
7-18. Определить температуру газа, находящегося в закрытом баллоне, если его давление увеличилось на 0,4 % первоначально при нагревании на
T = 1 К.
7-19. Тонкостенный резиновый шар собственным весом 0,6 Н наполнен неоном и погружен в озеро на глубину h = 120 м. Найти массу неона, если шар находится в положении равновесия. Атмосферное давление р0 = 1,03·105 Па, температура на глубине озера t = + 4 ºС. Натяжением резины пренебречь.
7-20. В закрытом сосуде емкостью V = 2 м3 находится т1 = 2,7 кг воды и т2 = 3,2 кг кислорода. Найти давление в сосуде при температуре t = 527 ºС, зная, что в этих условиях вся вода превращается в пар (считать, что пар в данном случае подчиняется законам идеального газа).
7-21. В теплоизолированный сосуд объемом V = 2 л, содержащий одноатомный идеальный газ при температуре Т1 = 300 К, помещают кусочек железа массой m = 100 г, нагретый до температуры Т2 = 500 К. Определить давление р2 газа после установления теплового равновесия, если его начальное давление равно р1 = 105 Па. Объемом железа по сравнению с объемом сосуда пренебречь. Удельная теплоемкость железа с = 0,46 · 103 Дж/кг·К.
7-22. В идеальном газе происходят процессы 1-2; 2-3; 3-4. Изобразить эти процессы на координатных осях р–T, р–V.
7-23. В лифте, движущимся с ускорением а = 5 м/с2, направленным вверх, находится цилиндрический сосуд, закрытый поршнем массой М = 20 кг и площадью S = 100 см2. Под поршнем находится идеальный газ. Поршень расположен на расстоянии h = 22 см от дна сосуда. Определите, на
74

какую величину h переместится поршень, если лифт будет перемещаться с тем же по модулю ускорением, направленным вниз. Температура газа не изменяется, атмосферное давление p0 = 105 Па. Ускорение свободного падения поршня g = 10 м/с2. Трением поршня о стенки сосуда пренебречь.
7-24. В цилиндре под невесомым поршнем площадью S = 100 см2 находится 1 моль идеального газа при температуре t1 = 100 ºС. К поршню через два блока на невесомой нерастяжимой нити подвешен груз массой М = 17 кг. На какую высоту h поднимется груз, если охладить газ до температуры t2 = 0 ºС. Атмосферное давление p0 = 105 Па. Трением пренебречь.
7-25. В вертикально расположенном цилиндрическом сосуде находится идеальный газ массой m с молярной массой . Газ отделен от атмосферы поршнем, соединенным с дном сосуда с пружиной жесткости k. При температуре T1 поршень расположен на расстоянии h от дна сосуда. До какой температуры T2 надо нагреть газ, чтобы поршень поднялся до высоты H = 2h? Поршень считать невесомым. Атмосферное давление p0.
7-26. Два сосуда, содержащие одинаковые массы одного газа, соединены трубкой с краном. В первом сосуде давление р1 = 5·103 Па, во втором – р2 = 8·103 Па. Какое давление установится после открытия крана, если температура остается неизменной?
7-27. Найти отношение средних квадратичных скоростей молекул гелия и азота при одинаковых температурах.
7-28. Какое число молекул двухатомного газа содержится в сосуде объемом 20 см3 при давлении р = 1,06·104 Па и температуре t = 27 ºС? Какой энергией теплового движения обладают эти молекулы?
7-29. Над газом совершен цикл 1-2-3-4-1. Начертите график этого цикла на осях координат V, T; p, T; p, .
7-30. Газ, занимающий при температуре Т1 = 100 ºК и давлении р1 = 0,2 МПа объем V1 = 1 л, изотермически сжимают до объема V2 и давления р2, затем изобарно охлаждают до температуры Т3 = 50 ºК, после чего изотермически изменяют объем до V4 = 0,5 л. Найти конечное давление р4. Построить графики этих процессов в координатах р, V; р, Т.
75
8.ЭЛЕМЕНТЫ СТАТИСТИЧЕСКОЙ ФИЗИКИ
Основные формулы
1. Распределение Больцмана (распределение частиц в силовом поле)
n n0e UkT ,
где п – концентрация частиц; U – их потенциальная энергия; п0 – концентрация частиц в точках поля, где U = O; k – постоянная Больцмана; T – термодинамическая температура; е – основание натуральных логарифмов.
2. Барометрическая формула (распределение давления в однородном поле силы тяжести)
p p e mgh/ kT , или | p h e gh/ RT , |
где р – давление газа; т – масса частицы; – молярная масса; h – высота точки по отношению к уровню, принятому за нулевой; р0 – давление на этом уровне; g – ускорение свободного падения; R – универсальная газовая постоянная.
3. Вероятность того, что физическая величина х, характеризующая молекулу, лежит в интервале значений от х до х + dх, равна
dW x f x dx,
где f(х) – функция распределения молекул по значениям данной физической величины х (плотность вероятности).
4. Количество молекул, для которых физическая величина х, характеризующая их, заключена в интервале значений от х до х + dх,
dN NdW x N f x dx.
5. Распределение Максвелла (распределение молекул по скоростям) выражается двумя соотношениями:
а) число молекул, скорости которых заключены в пределах от vдо v + dv,
m | 3/2 | 2 | / 2kT v |
dN v N f v dv 4 N | e mv | 2dv, | |
2 kT | |||
где f (v) – функция распределения молекул по абсолютным значениям скоростей, выражающая отношение вероятности того, что скорость молекулы лежит в интервале от v до v + dv, к величине этого интервала, а также долю числа молекул, скорости которых лежат в указанном интервале; N – общее число молекул; т – масса молекулы;
б) число молекул, относительные скорости которых заключены в пределах от и до и + dи,
dN u N f u du | 4 | Ne u2 u2du, | |
76 | |||

где u v/vв – относительная скорость, равная отношению скорости v к наи-
вероятнейшей скорости vв; f(и) – функция распределения по относительным скоростям.
6. Среднее число соударений, испытываемых одной молекулой газа в единицу времени,
z2 d2nv,
где d – эффективный диаметр молекулы; п – концентрация молекул; v –
средняя арифметическая скорость молекул.
7. Средняя длина свободного пробега молекул газа
8. Импульс (количество движения), переносимый молекулами из одного слоя газа в другой через элемент поверхности,
dp dv/dz S dt,
где – динамическая вязкость газа; dv/dz – градиент (поперечный) скорости течения его слоев; S – площадь элемента поверхности; dt – время переноса.
9. Динамическая вязкость
13 vl,
где – плотность газа (жидкости); v – средняя скорость хаотического дви-
жения его молекул; l – их средняя длина свободного пробега. 10. Закон Ньютона
F dp/dt dv/dz S,
где F – сила внутреннего трения между движущимися слоями газа. 11. Закон Фурье
Q K dT /dx S t,
где Q – теплота, прошедшая посредством теплопроводности через сечение площадью S – за время t; К – теплопроводность; dT/dx – градиент температуры.
12. Теплопроводность (коэффициент теплопроводности) газа
K 1 3cV v | l , или K 1 6kn v l , |
где сV – удельная теплоемкость газа при постоянном объеме; – плотность газа; v – средняя арифметическая скорость его молекулы; l – средняя длина свободного пробега молекул.
77
Источник
