Какими свойствами обладают углы равнобедренного треугольника

Содержание:

Свойства равнобедренного треугольника.
Признаки равнобедренного треугольника.
Формулы равнобедренного треугольника:
- формулы длины стороны;
- формулы длины равных сторон;
- формулы высоты, медианы, биссектрисы равнобедренного треугольника.

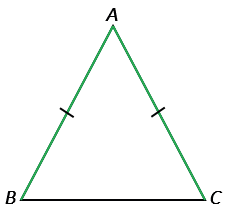
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.

АВ = ВС — боковые стороны

АС — основание

Свойства равнобедренного треугольника

Свойства равнобедренного треугольника выражаются через 5 теорем:

Теорема 1. В равнобедренном треугольнике углы при основании равны.

Доказательство теоремы:

Рассмотрим равнобедренный Δ ABC с основанием АС.

Боковые стороны равны АВ = ВС,

Следовательно углы при основании ∠ BАC = ∠ BСA.

Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника

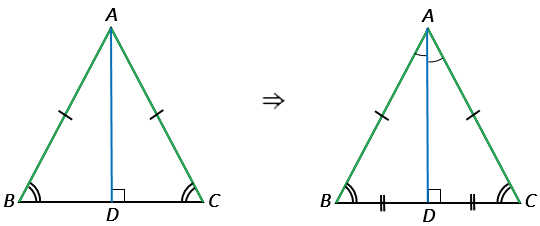
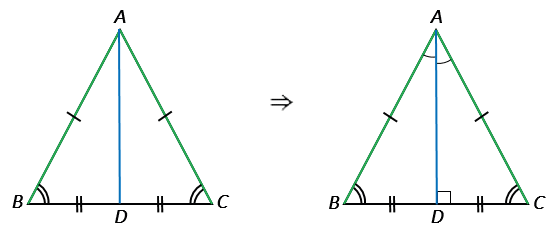
Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.

Доказательство теоремы:

Дан Δ ABC.
Из точки В проведем высоту BD.
Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
Прямые АС и BD называются перпендикуляром.
В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).
АВ = ВС — боковые стороны равны.
Стороны АD = СD, т.к. точка D отрезок делит пополам.
Следовательно Δ ABD = ΔBCD.
Биссектриса, высота и медиана это один отрезок – BD

Вывод:

Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.

Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.

Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство теоремы:

Дано два Δ ABC и Δ A1B1C1. Стороны AB = A1B1; BC = B1C1; AC = A1C1.

Доказательство от противного.

Пусть треугольники не равны (а то треугольники были равны по первому признаку).
Пусть Δ A1B1C2 = Δ ABC, у которого вершина C2 лежит в одной полуплоскости с вершиной C1 относительно прямой A1B1. По предположению вершины C1 и C2 не совпадают. Пусть D – середина отрезка C1C2. Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
Отсюда пришли к противоречию и теорему доказали.

Признаки равнобедренного треугольника

Если в треугольнике два угла равны.
Сумма углов треугольника 180°.
Если в треугольнике биссектриса является медианой или высотой.
Если в треугольнике медиана является биссектрисой или высотой.
Если в треугольнике высота является медианой или биссектрисой.

Формулы равнобедренного треугольника

Формулы сторон равнобедренного треугольника

b — сторона (основание)
а — равные стороны
a — углы при основании
b — угол образованный равными сторонами

Формулы длины стороны (основания — b):

b = 2a sin( beta /2)= a sqrt { 2-2 cos beta }
b = 2a cos alpha

Формулы длины равных сторон — (а):

a=frac { b } { 2 sin(beta /2) } = frac { b } { sqrt { 2-2 cos beta } }
a=frac { b } { 2 cosalpha }

Формулы высоты, медианы, биссектрисы равнобедренного треугольника

L — высота=биссектриса=медиана
b — сторона (основание)
а — равные стороны
a — углы при основании
b — угол образованный равными сторонами

Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):

L = a sina
L = frac { b } { 2 } *tgalpha
L = a sqrt { (1 + cos beta)/2 } =a cos (beta)/2)

Формула высоты, биссектрисы и медианы, через стороны, (L):

L = sqrt { a^ { 2 } -b^ { 2 } /4 }

Площадь равнобедренного треугольника

b — сторона (основание)
а — равные стороны
h — высота

Формула площади треугольника через высоту h и основание b, (S):

S=frac { 1 } { 2 } *bh

Смотри также:

Теорема о сумме углов треугольника
Формулы площади поверхности, основания, сечения призмы
Площадь поверхности куба, формулы и примеры
Основные формулы по математике
Справочные материалы ЕГЭ от ФИПИ по математике

Источник

Главная
Справочники
Справочник по геометрии 7-9 класс
Треугольники
Свойства равнобедренного треугольника

1. Теорема

Дано: АВС – равнобедренный, ВС – основание.

Доказать: В = С.

Доказательство:

Какими свойствами обладают углы равнобедренного треугольника

Проведем биссектрису АD из вершины А к стороне ВС.

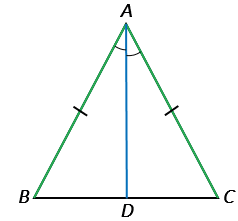
Какими свойствами обладают углы равнобедренного треугольника

Рассмотрим АВD и АСD: АВ = АС по условию (АВС – равнобедренный), АD – общая сторона, BAD = CAD, так как АD – биссектриса по построению, АВD = АСD по первому признаку равенства треугольников В = С,потому что в равных треугольниках против равных сторон лежат равные углы (В лежит против стороны АС, С. – против стороны АВ).

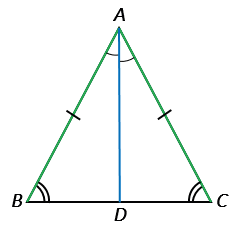
Какими свойствами обладают углы равнобедренного треугольника

Теорема доказана.

Справедливо и обратное утверждение:

Если в каком-либо треугольнике два угла равны, то такой треугольник равнобедренный.

2. Теорема

В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Дано: АВС – равнобедренный, ВС – основание, АD – биссектриса.

Доказать: АD – медиана и высота.

Доказательство:

Какими свойствами обладают углы равнобедренного треугольника

Рассмотрим АВD и АСD: АВ = АС по условию (АВС – равнобедренный), АD – общая сторона, BAD = CAD, так как АD – биссектриса по условию, АВD = АСD по первому признаку равенства треугольников ВD = DC и ADВ = ADС.

Мы доказали, что ВD = DC точка D – середина стороны ВС, тогда АD является медианой АВС (по определению медианы).

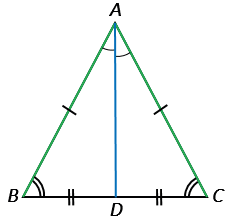
Какими свойствами обладают углы равнобедренного треугольника

Мы доказали, что ADВ = ADС, причем ADВ и ADС – смежные углы, поэтому ADВ + ADС = 1800, тогда ADВ = ADС =900, т.е. АDBC, а это означает, что AD является высотой АВС (по определению высоты).

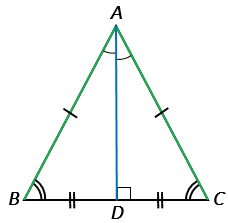
Какими свойствами обладают углы равнобедренного треугольника

Теорема доказана.

Справедливо и обратное утверждение:

Если в каком-либо треугольнике медиана и высота совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника.

3. Теорема

В равнобедренном треугольнике высота, проведённая к основанию, является медианой и биссектрисой.

Справедливо и обратное утверждение:

Если в каком-либо треугольнике медиана и биссектриса совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника.

4. Теорема

В равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой.

Справедливо и обратное утверждение:

Если в каком-либо треугольнике высота и биссектриса совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника.

Важно помнить, что данные теоремы справедливы только в том случае, если высота, медиана и биссектриса равнобедренного треугольника проведены к его ОСНОВАНИЮ.

Если треугольник равносторонний, то данные теоремы справедливы для медиан, биссектрис и высот, проведенных к каждой из сторон треугольника.

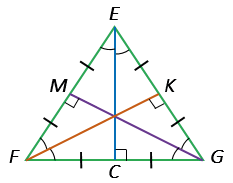
Какими свойствами обладают углы равнобедренного треугольника

EFG – равносторонний:

ЕС – биссектриса, медиана и высота, проведенная к стороне FG,
FK – биссектриса, медиана и высота, проведенная к стороне ЕG,
GM – биссектриса, медиана и высота, проведенная к стороне ЕF.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Треугольник

Равенство треугольников

Первый признак равенства треугольников

Перпендикуляр к прямой

Медианы треугольника

Биссектрисы треугольника

Высоты треугольника

Равнобедренный треугольник

Второй признак равенства треугольников

Третий признак равенства треугольников

Окружность

Построения циркулем и линейкой

Треугольники

Правило встречается в следующих упражнениях:

7 класс

Задание 162,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 6,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 298,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 315,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 317,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 408,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 437,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 530,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 856,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1212,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Тема урока: Свойства равнобедренного треугольника.

Предмет: геометрия

Класс: 7 класс

Тип урока: урок изучения и первичного закрепления знаний

Используемые учебники и учебные пособия: Л.С.Атанасян и др. Геометрия 7-9.

Используемое оборудование: компьютер, мультимедийный проектор

Цели урока: создание условий для организации совместной и самостоятельной деятельности обучающихся по изучению свойств равнобедренного треугольника и овладению умением решать задачи с использованием изученных свойств.

образовательная: обобщить, систематизировать, расширить и углубить знания учащихся по теме треугольники и его виды, закрепить навыки и умения, используя определения и теоремы, ознакомить со свойствами равнобедренного треугольника и научить применять их при решении задач.

развивающая: развитие математической речи учащихся, их памяти, внимания, наблюдательности, умения сравнивать, обобщать, обоснованно делать выводы; развивать умение преодолевать трудности при решении задач.

воспитательная: воспитание навыков контроля и самоконтроля, аккуратности, внимательности, позитивного отношения к обучению, умения работать в коллективе.

ХОД УРОКА

I. Организационный момент

II. Повторение основных понятий

На данном этапе урока повторяем изученные ранее понятия: “медиана”, “биссектриса”, “высота” треугольника. Я предлагаю повторить эти понятия, используя тест «Медианы, биссектрисы и высоты треугольника». Повторение ведётся посредством фронтального опроса учащихся. (слайды

Задание 1

Вопрос:

Отрезок, соединяющий вершину треугольника с серединой противолежащей стороны, называется …

Задание 2

Вопрос:

Перпендикуляр, опущенный из вершины треугольника на противоположную сторону или её продолжение, называется …

Задание 3

Вопрос:

В треугольнике АВС отрезок ВD делит угол АВС на два равных угла. Как называется отрезок ВD?

Изображение:

Задание 4

Вопрос:

В треугольнике провели две медианы. Сколько всего треугольников изображено на рисунке?

Изображение:

Выберите один из 4 вариантов ответа:

1) Четыре

2) Шесть

3) Восемь

4) Двенадцать

Задание 5

Вопрос:

В треугольнике АВС отрезок AD является медианой. Чему равна длина стороны ВС, если длина отрезка BD равна 3 см?

Изображение:

Выберите один из 4 вариантов ответа:

1) 9 см

2) 6 см

3) 5 см

4) 3 см

Задание 6

Вопрос:

Чему равна градусная мера угла ВАС, если АD – биссектриса треугольника АВС, а угол ВАD равен 35°?

Изображение:

Выберите один из 4 вариантов ответа:

1) 35°

2) 90°

3) 70°

4) 45°

Задание 7

Вопрос:

Может ли точка пересечения высот лежать вне треугольника?

Выберите один из 2 вариантов ответа:

1) Может

2) Не может

Задание 8

Вопрос:

Сколько высот имеет любой треугольник?

Выберите один из 4 вариантов ответа:

1) Четыре

2) Одну

3) Две

4) Три

Задание 9

Вопрос:

Отрезок ВD – медиана треугольника АВС, отрезок ВЕ – медиана треугольника DBC. Чему равна длина отрезка ЕС, если отрезок АС равен 20 см?

Изображение:

Выберите один из 4 вариантов ответа:

1) 15 см

2) 10 см

3) 5 см

4) 4 см

Задание 10

Вопрос:

Чему равна градусная мера углаАDB, если отрезок BD – высота треугольника АВС?

Выберите один из 4 вариантов ответа:

1) 30°

2) 60°

3) 90°

4) 120°

Ответы:

1) Верный ответ: “медианой”.

2) Верный ответ: “высотой”.

3) Верный ответ: “Биссектрисой треугольника”.

4) Верный ответ: 3;

5) Верный ответ: 2;

6) Верный ответ: 3;

7) Верный ответ: 1;

8) Верный ответ: 4;

9) Верный ответ: 3;

10) Верный ответ: 3;

Итог: Молодцы ребята. Вы хорошо применяете определения и формулировки свойств геометрических фигур при решении задач.

Итак, мы с вами повторили теоретический материал прошлых уроков, который нам понадобится при изучении новой темы «Свойства равнобедренного треугольника».

III. Объяснение нового материала

Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которой человек узнал ещё в глубокой древности. Например, то, что в равнобедренном треугольнике, с которым мы сегодня познакомимся, углы при основании равны, было известно ещё древним вавилонянам 4000 лет назад. Равнобедренный треугольник обладает ещё рядом геометрических свойств, которые всегда имели широкое применение в практической жизни.

Выясним, какой треугольник называется равнобедренным, и какими свойствами он обладает.

Откройте тетради, запишите число, классная работа и тему сегодняшнего урока «Свойства равнобедренного треугольника»

1. Вводится понятие равнобедренного треугольника и его элементов.

Вспомните из курса математики, какой треугольник называется равнобедренным?

– Треугольник, две стороны которого равны, называется равнобедренным. Равные стороны называются боковыми, а третья сторона – основанием равнобедренного треугольника.

– Назовите угол, лежащий напротив основания треугольника, назовите углы при основании равнобедренного треугольника. (слайд № 10) Изобразите данный треугольник к себе в тетрадь.

2. Вводится понятие равностороннего треугольника.

– Треугольник, все стороны которого равны, называется равносторонним.

4. Рассматриваем свойство об углах равнобедренного треугольника.

В равнобедренном треугольнике углы при основании равны.

Работа с формулировкой теоремы: разбираем, что дано, что доказать. Рассматриваем доказательство теоремы 1. Проведём биссектрису из вершины А треугольника к основанию ВС. Предлагаю учащимся продолжить доказательство самостоятельно (в процессе рассуждений, по щелчку “мыши” появляются записи на экране)

Теорема. В равнобедренном треугольнике углы при основании раны

Дано: Δ АВС – ………………

Доказать: …………

В C

Доказательство.

Проведем биссектрису АF.
Рассмотрим ……… и ………..:

……. = …….. (т.к. Δ АВС – ………………);
……. = ………( т.к. АF – …………..Δ АВС ); ………….. = …………..
……….. – …………….. (по двум сторонам и углу между ними)

Тогда ……… = ………., ч.т.д.

5. Свойство биссектрисы, проведённой к основанию равнобедренного треугольника, можно предложить учащимся получить самостоятельно (это зависит от уровня подготовки класса), проведя практическую работу по группам:

– Постройте равнобедренный треугольник

– Проведите биссектрису из вершины треугольника к его основанию

– Вы знаете, что она делит угол пополам, но как вы думаете, глядя на рисунок, каким ещё свойством обладает эта биссектриса? При обсуждении подумайте:

– Любая ли биссектриса равнобедренного треугольника является ли его высотой и медианой? (Можно предложить построить все биссектрисы треугольника).

– Является ли биссектриса равнобедренного треугольника его высотой и медианой? Если да, то какая из трёх?

6. Записываем свойство в виде теоремы 2.

Теорема. В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой (в процессе рассуждений, по щелчку “мыши” появляются записи на экране)

A Дано:

Δ АВС – ………………

AF – ……………… Δ АВС

B С Доказать: AF -………….. Δ АВС, AF -………….. Δ АВС

Доказательство.

Рассмотрим ……… и ………..:

……. = …….. (т.к. ΔАВС – ………………);
……. = ………( т.к. AF – …………..Δ АВС ); ………….…………..
……….. – ……………..

(по двум сторонам и углу между ними)

Тогда ……… = ………., AF – ……………….. Δ АВС.

Тогда ……. = ……., а т.к. …… и …… – смежные, ……. = ……. = ….о, т.е. AF……, значит, AF – ……………….. Δ АВС, ч.т.д.

IV. Закрепление пройденного

Устное решение задач

Какие из данных треугольников являются равнобедренными, почему?

Треугольник АВС – равнобедренный ∠МАВ = 100, найдите∠А и ∠С в треугольнике АВС

Треугольник АВС – равнобедренный, АС – основание, ВD – биссектриса, ∠СВD = 37, АС = 25 см. Найдите∠В, ∠ВDС и DC.

Решение задачи № 107 из учебника на доске и в тетрадях.

Самостоятельное решение № 112 с последующей проверкой

Дано: АВ=ВС, ∠1=130. Найдите ∠2

Решение:

Углы ∠ 1 и ∠АСВ – смежные, т.е∠1 + ∠АСВ=180 , значит

∠АСВ = 180 – 130= 50АВС – равнобедренный,

значит ∠ВАС = ∠АСВ=50 (углы при основании равнобедренного треугольника)

∠2 = ∠ВАС = 50( каквертикальные)

Ответ: ∠ 2= 50

V. Итоги урока

1. Фронтальный опрос:

Какой треугольник называется равнобедренным?
Какой треугольник называется равносторонним?
Является ли равносторонний треугольник равнобедренным?
Каким свойством обладают углы равнобедренного треугольника?
Каким свойством обладает биссектриса равнобедренного треугольника?
Любая ли биссектриса обладает этим свойством? Какая?
Любая ли биссектриса равностороннего треугольника обладает этим свойством?

2. Домашнее задание: п.18, вопросы 10 – 18, №№ 109, 117

Используемая литература

Учебник “Геометрия. 7 – 9” авторов: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадышев, Э.Г.Позняк, И.И. Юдина (М., Просвещение, 1990 и последующие издания).

“Задачи и упражнения на готовых чертежах. 7 – 9 классы. Геометрия” автор: Е.М.Рабинович (М.: Илекса, Харьков:Гимназия, 2001)

Изучение геометрии в 7, 8, 9 классах: Методические рекомендации к учебнику: Книга для учителя. Л.С. Атанасян, В.Ф.Бутузов, Ю.А.Глазков и др. (М.: Просвещение, 2003)

Поурочные разработки по геометрии. 7 класс. Гаврилова Н.Ф. (М.: “ВАКО”, 2004).

Источник

Конспект урока по геометрии. 7 класс.

Тема: «Свойства равнобедренного треугольника».

Тип: урок получения новых знаний, умений и навыков.

Цель урока: Организация деятельности учащихся по изучению материала по теме «Свойства равнобедренного треугольника». .

Учебные задачи:

Личностные:

продолжать развивать умение ясно, точно и грамотно излагать свои мысли в устной и письменной речи,
развивать креативность мышления, инициативу, находчивость, активность при решении математических задач.

Метапредметные:

расширять кругозор, прививать умение совместно работать (чувство товарищества и ответственности за результаты своего труда);
продолжать развивать умение понимать и использовать математические средства наглядности.

Предметные:

закрепить понятия биссектрисы, высоты и медианы треугольника, понятия перпендикуляра к прямой;
выполнить лабораторную работу «Свойства равнобедренного треугольника», сделать вывод;
доказать свойства равнобедренного треугольника;
формировать умение применять эти свойства,

Воспитательные:

воспитывать самостоятельность, аккуратность при выполнении рисунков к условию задачи;
воспитывать у учащихся уважение к одноклассникам при просмотре презентаций , при работе парами;

воспитывать культуру математической речи.

Методы и приёмы: исследовательский, проблемно-поисковый, репродуктивный; работа с учебником, индивидуальная работа с самопроверкой.

Технологии: технология деятельностного метода обучения с использованием элементов проблемного обучения, элементов исследования, здоровьесбережения, ИКТ-технологии.

Оборудование: учебник Геометрия : 7 – 9. Учебник для 7 – 9 классов средней школы.; авторы: Л. С. Атанасян, В.Ф. Бутузов С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина , М., «Просвещение», 2013 ; доска, мел, компьютер, проектор, компьютерная мультимедийная презентация «Свойства равнобедренного треугольника», распечатки материалов для самостоятельной работы учащихся.

План урока:

Ход урока.

Организационный момент .(Слайд №1)

Цель: формирование мотивации.

Учитель: Сегодня мы продолжим знакомство с самой популярной в школьном курсе геометрической фигурой. Это самая простая замкнутая прямолинейная фигура, свойства которой человек узнал еще в глубокой древности, так как она имела широкое применение в практической жизни. Вы догадались, что это за фигура? – Треугольник. Откройте тетради запишите число, классная работа.

Актуализация опорных знаний. Тест по готовым рисункам, проверка ответов: 1 этап – в паре, 2 этап –

фронтально.

Цель: повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в

индивидуальной деятельности каждого учащегося.

Учитель: Как вы думаете, на какие вопросы вы должны знать ответ, изучив темы «Первый признак равенства треугольников», «Медианы, биссектрисы и высоты треугольника»?

Учащиеся задают вопросы и отвечают на них:

Что называется треугольником?
Элементы треугольника? Периметр треугольника?
Первый признак равенства треугольников?
Какие отрезки называются медианой, биссектрисой и высотой треугольника? Сколько высот, медиан, биссектрис в треугольнике?

Повторив теоретический материал, предлагается ученикам самостоятельно ответить на вопросы теста, ответы записать в тетрадь.

Тест: (Слайд №2, №3)

№1. На каком рисунке построена высота?

№2. На каком рисунке построена медиана?

№3. На каком рисунке построена биссектриса?

№4. На каком рисунке есть равные треуголь-

ники?

Постановка учебной задачи.

Цель: обсуждение затруднений («Почему возникли затруднения?», «Чего мы еще не знаем?»).

№1

№2

№3

№4

Ответ

2, 3

1, 2

1, 3

2, 3?

Проверка ответов теста (Слайд 4):

После проверки в паре, учитель предлагает сильному ученику прокомментировать ответы. Затруднение вызывает ответ к последней задаче.

Учитель: Почему нельзя ответить на вопрос в последней задаче? – Мы не знаем, равны ли углы А и В?

«Открытие» учащимися нового знания

Цель: устранение возникшего затруднения решения задачи и обсуждение проекта ее решения, формулировка темы и цели урока.

После обсуждения, учащиеся выдвигают гипотезу: если сможем установить равенство углов А и В, то ответ в задании №4 – 2, 3.Учитель предлагает проанализировать рисунок. В ходе беседы учащиеся определяют вид треугольника АВС (Слайд №5), повторяют определение равнобедренного треугольника, его элементы: боковые стороны, основание, углы при основании и угол, противолежащий основанию. Опираясь на выдвинутую гипотезу и предыдущие рассуждения, учащиеся формулируют тему урока и его цель (Слайд №6,№7). Записывают тему в тетрадь.

Учитель: Продолжаем работать с равнобедренным треугольником. Кто может растолковать понятие «свойство»? Что это такое? Что нам предстоит выяснить? В толковом словаре сказано, что «свойство – качество, признак, составляющий отличительную особенность чего-нибудь». А чтобы эту отличительную особенность выяснить, мы проведем исследование. (Слайд №8)Ученики работают с листами №1.( Приложение 1 ).

Исследовательская работа (Слайд №8)

Цель исследовательской работы: выяснить, какими свойствами обладает равнобедренный треугольник

Оборудование: линейка, транспортир.

Задание 1. Измерьте углы при основаниях треугольников.(1 вариант АВС, 2 вариант ОМК )

;О = ; А = 

.К = ; С= 

Сделайте вывод:

В равнобедренном треугольнике углы при основании _ равны__

Учитель предлагает ученикам сформулировать теорему об углах равнобедренного треугольника. (слайд №9).

Теорема. В равнобедренном треугольнике углы при основании равны.

Частично стёрты записи доказательства на доске. (Обратная сторона доски). Необходимо их восстановить. Смотрите, думайте, кто догадался – поднимает руку. Старайтесь понять и запомнить доказательство, проще будет дома повторить.

Дано

Δ АВС – ………………

Доказать: ∟… = ∟…..

Доказательство.

Проведем биссектрису ВD.
Рассмотрим Δ ……… и Δ ………..:

АВ = …….. (т.к. Δ АВС – равнобедренный);
∟АВD = ………(т.к. ВD – ………Δ АВС ); ………….. = …………..
……….. – общая сторона (по двум сторонам и………………)

Тогда ……… = ………., ч. т.д.

Учащиеся делают чертёж в тетради, выполняют соответствующие записи, доказывают теорему. При необходимости руководствуются учебником. (п.23)

Учитель: Вернемся к нерешенной задаче теста. – Гипотеза подтвердилась, ответ 2 и 3. (слайд №10, №11).

Задание2 .(1 вариант АВС, 2 вариант ОМК )

В треугольниках из вершин B и М к основаниям AC и ОK соответственно проведите:

медиану красным цветом;
биссекктрису синим цветом,
высоту зеленым цветом.

Проанализируйте результаты и сделайте вывод:

В равнобедренном треугольнике медиана, проведённая к основанию является и биссектрисой и высотой. (слайд №12).

Учитель предлагает ученикам сформулировать теорему о свойстве медианы равнобедренного треугольника, проведённой к основанию.

Учащиеся отвечают на вопросы: что дано в теореме? И что надо доказать?

Учитель: Доказательство теоремы выполните дома.

Учитель: Можно ли утверждать, что биссектриса, медиана и высота, проведенные к основанию, совпадают? – Да.

Физкультминутка.

Все умеем мы считать

Раз, два, три, четыре, пять —

Раз! Подняться потянуться. (Под счет ученика дети выполняют потягивания.)

Два! Согнуться, разогнуться. (Наклоны. Повороты туловища.)

Три! В ладоши три хлопка,

Головою три кивка. (Движения головой.)

На четыре – руки шире. (Хлопки в ладоши.)

Пять — руками помахать. (Движения руками.)

Шесть — за парту тихо сесть.

6. Включение в систему знаний «новых» знаний..

Цель: научить применять изученные свойства при решении задач.

Найдите угол KBA.

7. Самостоятельная работа с взаимопроверкой . Задание лежит на парте.

Цель: контроль усвоения изученных свойства при решении задач. (Слайд № 15)

2 Вариант

По окончанию работы ученики обмениваются тетрадями и проверяют решение . (Слайд 16)

Решение и ответы

Вариант 1

Вариант2

МР = МD, ΔРМD – равнобедренный.
MPD = MDP = 68° – углы при основании.
1 = 180° – MPD = 180° – 68° = 112°.

Ответ: 112°

AC = AD, ΔACD – равнобедренный.
ADC = MDD = 40° – вертикальные углы.
С = ADC = 40°- углы при основании.

Ответ: 40°

FN = NE = 14 см, Δ FNE – равнобедренный.
NL – высота и медиана, по свойству равнобедренного треугольника; FL = LE = 5 cм.
EF = FL + LE = 5 + 5 = 10 (cм).
PFNE = FN+NE+FE,

PFNE =14+14+10=28(см).

Ответ: 28 см.

AМ = MG = 10 см, Δ AMG – равнобедренный.
AG = PAMG – AM – MG =28- 10-10 = 8 (см).
ME – биссектриса и медиана, по свойству равнобедренного треугольника; AE = EG = AG : 2 = 8 : 2 = 4(cм).

Ответ: 4 см.

Подведение итогов:

Цель: Рефлексия учебной деятельности .(Слайд №17)

Учитель предлагает учащимся ответить на следующие вопросы:

Что вы узнали на уроке?
Какая была цель урока?

С чем познакомились на уроке?
Какими свойствами обладает равнобедренный треугольник?
Где эти свойства можем использовать? (при решении задач и доказательстве теорем).

Учитель предлагает оценить каждому свою работу на уроке и выставить отметку в тетрадь.

9.Задание на дом. .(Слайд №18)

п.23, п.26 в.4 в.11- письменно.
Задача №11 -2, №22- дополнительно по желанию.

Приложение №1.

Исследовательская работа

Задание 1. Измерьте углы при основаниях треугольников. (1 вариант АВС, 2 вариант ОМК )

;О = ; А = 

.К = ; С= 

Задание 2. ( 1 вариант АВС, 2 вариант ОМК )

В треугольниках из вершин B и М к основаниям AC и ОK соответственно проведите:

медиану красным цветом;
биссекктрису синим цветом,
высоту зеленым цветом.

Приложение №2.

Самостоятельная работа.

2 Вариант

Источник