Какими свойствами обладают стороны четырехугольника

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)
Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Виды четырехугольников: | |||
| |||
| |||
| |||
| |||
|  | ||
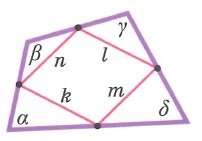
Свойства произвольных четырехугольников: | |||
|  | ||
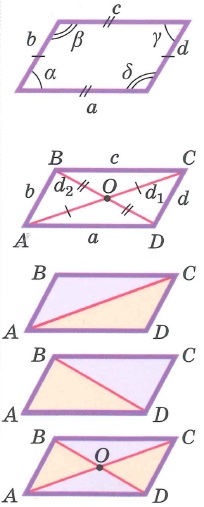
Свойства параллелограмма: | |||
|  | ||
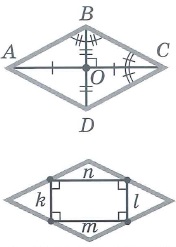
Свойства ромба: | |||
|  | ||
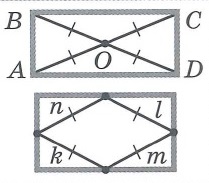
Свойства прямоугольника: | |||
|  | ||
Свойства квадрата: | |||
| |||
Свойства трапеции: | |||
| 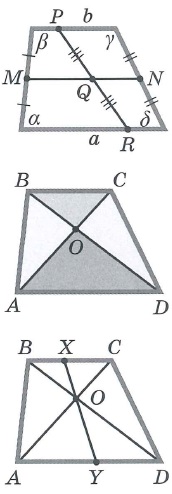 | ||
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
Источник
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырехугольники бывают выпуклые (ABCD) и невыпуклые (A1B1C1D1).
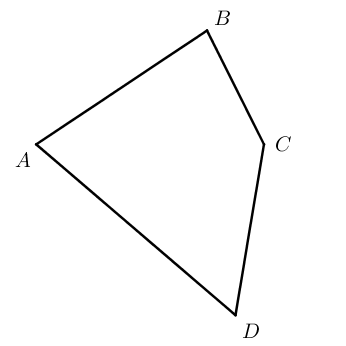
В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.
Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: AB и AD, AB и BC, BC и CD, CD и AD.
Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: AB и CD, BC и AD.
Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C, B и D.
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. AC и BD – диагонали четырехугольника ABCD.
Диагонали выпуклого четырехугольника пересекаются в одной точке.
Площадь произвольного выпуклого четырехугольника можно найти по формуле:
S=12d1d2⋅sinφ
где d1 и d2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).
Рассмотрим более подробно некоторые виды выпуклых четырехугольников.
Класс параллелограммов: параллелограмм, ромб, прямоугольник, квадрат.
Класс трапеций: произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма:
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180°.
- Сумма квадратов диагоналей равна сумме квадратов сторон. d12+d22=2(a2+b2)
Площадь параллелограмма можно найти по трём формулам.
S=a⋅ha=b⋅hb
Как произведение стороны и высоты, проведенной к ней.
Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.
S=a⋅b⋅sinα
Как произведение двух смежных (соседних) сторон на синус угла между ними.
S=12⋅d1⋅d2⋅sinφ
Как полупроизведение диагоналей на синус угла между ними.
Ромб – параллелограмм, у которого все стороны равны.
Свойства ромба:
- Диагонали пересекаются под прямым углом.
- Диагонали являются биссектрисами углов, из которых выходят.
- Сохраняются все свойства параллелограмма.
Площадь ромба можно найти по трём формулам.
S=a⋅h
Как произведение стороны ромба на высоту ромба.
S=a2⋅sinα
Как квадрат стороны ромба на синус угла между двумя сторонами.
S=12⋅d1⋅d2
Как полупроизведение диагоналей ромба.
Прямоугольник – это параллелограмм, у которого все углы равны 90°.
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Сохраняются все свойства параллелограмма.
Площадь прямоугольника можно найти по двум формулам:
S=a⋅b
Как произведение двух смежных (соседних) сторон прямоугольника.
S=12⋅d2⋅sinφ
Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.
Квадрат – прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Сохраняет свойства ромба.
- Сохраняет свойства прямоугольника.
Площадь квадрата можно вычислить по двум формулам:
S=a2
Как квадрат стороны.
S=d22
Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.
Стороны, которые параллельны друг другу называются основаниями, другие две стороны называются боковыми сторонами.
BC и AD – основания, AB и CD – боковые стороны трапеции ABCD.
Свойства трапеции:
сумма углов, прилежащих к боковой стороне, равна 180°.
∠A+∠B=180°
∠C+∠D=180°
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Средняя линия параллельна основаниям. Её длина находится по формуле: m=a+b2
Площадь трапеции можно найти по двум формулам:
S=a+b2⋅h=m⋅h
Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.
S=12d1⋅d2⋅sinφ
Как полупроизведение диагоналей на синус угла между ними.
Виды трапеций
Прямоугольная трапеция – трапеция, у которой два угла прямые.
Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.
Свойство равнобокой трапеции: углы при основании равны
Модуль геометрия: задания, связанные с четырехугольниками
Скачать домашнее задание к уроку 4.
Источник
Инфоурок
›
Геометрия
›Презентации›Четырехугольники. Основные признаки и свойства

Описание презентации по отдельным слайдам:
1 слайд

Описание слайда:
Четырехугольники Пискунова И.В. учитель математики ГБОУ лицея №299
2 слайд

Описание слайда:
Найди четырехугольники B C D E M N K S O P L H A B C D M N O K R T F Q H Z I R Какая буква лишняя?
3 слайд

Описание слайда:
Четырехугольник Фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. А B C D
4 слайд

Описание слайда:
Основные элементы четырехугольника A, B, C, D – вершины четырехугольника A и B – соседние вершины AD, BC, CD, BA – стороны многоугольника AD и CD – смежные стороны многоугольника AB и CD – несмежные стороны AC, BD – диагонали многоугольника А B C D
5 слайд

Описание слайда:
Сумма углов выпуклого многоугольника Сумма углов выпуклого четырехугольника А B C D
6 слайд

Описание слайда:
Выпуклость четырехугольника
7 слайд

Описание слайда:
Виды четырехугольников Трапеция Четырехугольник Параллелограмм Квадрат Прямоугольник Ромб
8 слайд

Описание слайда:
Параллелограмм четырехугольник, у которого противоположные стороны попарно параллельны. A B C D
9 слайд

Описание слайда:
Свойства параллелограмма
10 слайд

Описание слайда:
Площадь параллелограмма
11 слайд

Описание слайда:
Прямоугольник Прямоугольник — параллелограмм, у которого все углы прямые.
12 слайд

Описание слайда:
Свойства прямоугольника Замечание: Справедливы также обратные утверждения. Их называют признаками прямоугольника.
13 слайд

Описание слайда:
Окружность, описанная около прямоугольника
14 слайд

Описание слайда:
Площадь прямоугольника
15 слайд

Описание слайда:
Ромб Ромб — параллелограмм, у которого все стороны равны.
16 слайд

Описание слайда:
Свойства ромба
17 слайд

Описание слайда:
Окружность, вписанная в ромб
18 слайд

Описание слайда:
Площадь ромба
19 слайд

Описание слайда:
Квадрат Квадрат— прямоугольник, у которого все стороны равны,
20 слайд

Описание слайда:
Свойства квадрата
21 слайд

Описание слайда:
Окружность, описанная около квадрата
22 слайд

Описание слайда:
Окружность, вписанная в квадрат
23 слайд

Описание слайда:
Площадь квадрата
24 слайд

Описание слайда:
Трапеция — четырехугольник, у которого ровно одна пара противолежащих сторон параллельна. Трапеция
25 слайд

Описание слайда:
Окружность, описанная около трапеции
26 слайд

Описание слайда:
Окружность, вписанная в трапецию
27 слайд

Описание слайда:
Площадь трапеции
Выберите книгу со скидкой:
БОЛЕЕ 58 000 КНИГ И ШИРОКИЙ ВЫБОР КАНЦТОВАРОВ! ИНФОЛАВКА
Инфолавка – книжный магазин для педагогов и родителей от проекта «Инфоурок»

Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки
Учитель математики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Номер материала:
ДБ-026361
Вам будут интересны эти курсы:
Оставьте свой комментарий
Источник
