Какими свойствами обладают средние величины

Среди показателей, характеризующих статистические совокупности, важное место занимают средние величины.
Средняя величина – показатель, который даёт обобщённую (усреднённую) характеристику единиц изучаемой совокупности. В средней величине отражается то общее, что имеется в каждой единице совокупности.
Сущность статистической обработки методом средней величины заключается в замене индивидуальных значений признака их средним показателем. При этом общий объём совокупности остаётся неизменным.

Пример: есть данные о выработке 5 рабочих: 135, 141, 153, 159, 162. Определить среднюю выработку. .
Средние величины, которые необходимо знать наизусть:
– средняя арифметическая;
– средняя гармоническая;
– средняя хронологическая;
– средняя квадратическая, кубическая;
– средняя геометрическая;
– структурные средние: мода, медиана.
1. Средняя арифметическая: чаще всего в статистике и социально-экономических исследованиях применяется арифметическая величина.
Средняя арифметическая простая рассматривается в случаях, когда значение признака повторяется один или одинаковое число раз в ряде распределения:

, где n-количество единиц совокупности.
Средняя арифметическая взвешенная применяется в случаях, когда каждое значение признака повторяется неодинаковое число раз, или частота ряда распределения превышает единицу хотя бы для одного признака:

, где f-вес.(сколько раз повторяется каждая еденица совокупности)
2. Средняя гармоническая: в ряде случаев бывают известны варианты (x) и произведения варианты на частоту (x•f), в то время как сами частоты (f) неизвестны, тогда применяется средняя гармоническая, которая бывает простой и взвешенной.
Произведение x•f выражается через сложный экономический показатель M (M= x•f). Для расчёта средней величины, когда x•f =M=1, применяется средняя гармоническая простая: .


Еслиx•f =M? 1, то для расчёта применяется средняя гармоническая взвешенная: .
Средняя гармоническая – величина, обратная средней арифметической, из обратных значений признака.
1. Если от каждой варианты отнять или прибавить одно и то же число, то средняя увеличится или уменьшится на то же число.
2. Если каждую варианту увеличить или уменьшить в a раз, то средняя увеличится или уменьшится в столько же раз.
3. Если все частоты увеличить или уменьшить в aраз, то средняя не изменится.
4. Если все частоты увеличить или уменьшить на a, то средняя изменится непредсказуемо.
5. Средняя арифметическая суммы нескольких величин равна суме средних арифметических этих величин.
6. Алгебраическая сумма отклонений значений признака от средней арифметической всегда равна нулю.
Пример: Найти среднюю урожайность в 2003 и 2004 гг.
№ колхоза | 2003 г. | 2004 г. | ||
урожайность (ц/га) | площадь (га) | урожайность (ц/га) | Валовой сбор(ц) | |
1 2 3 | 40 50 60 | 1000 2000 3000 | 38 49 65 | 40000 100000 150000 |
Решение:

, где f-вес
(ц/га)
.



(ц/га)
3. Средняя хронологическая: применяется для расчёта средней величины, если исходные данные представлены на определённые даты, моменты времени:

Пример: Найти среднюю стоимость ОПФ
дата | 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | 1.06 |
стоимость ОПФ | 100 | 120 | 110 | 120 | 140 | 140 |
Решение:

, ,
,
, .
Приведем все расчеты к одному знаменателю: Х=эээ






4. Средняя квадратическая: применяется для измерения вариации признака в совокупности:

,

5. Средняя кубическая: .

6. Средняя геометрическая: применяется чаще всего для определения средних темпов роста в единицу времени: , ,
Пример: Рассчитайте среднегодовые темпы роста
показатели | год | ||||
1995 | 1996 | 1997 | 1998 | 1999 | |
выпуск продукции | 20 | 22 | 26 | 50,1 | 100,2 |
х1 | х2 | х3 | х4 | х5 | |
коэффициент роста выпуска продукции | ? | 1,1 | 1,2 | 1,9 | 2 |
k1 | k2 | k3 | k4 |
Решение:

, где m=n-1.

.
Средняя геометрическая, чаще всего, применяется в экономических расчетах, но учитывает только начало и конец ряда и недостаточно точно отражает динамику изменения, т.е. она не учитывает сумму ряда.
7. Средняя кумулятивная:

.
Формула кумулятивной средней более чётко отражает динамику изменений и помогает увидеть сумму ранжированного ряда.

Все рассмотренные средние величины (кроме средней хронологической) являются степенными средними и выводятся из следующей формулы: , где получается при
k=-1 ?средняя гармоническая;
k=0 ? средняя геометрическая;
k=1 ?средняя арифметическая;
k=2 ?средняя квадратическая;
k=3 ?средняя кубическая.
Все эти показатели рассчитываются для варьирующего признака для простых средних. Если все значения признака в ряде распределения одинаковы, то все значения средних равны. Между указанными средними величинами имеет место зависимость (для одного ряда распределения):

? это неравенство называется правилом мажорантности средних величин.
8. Структурные средние:

1) Структурное среднее мода (Mо) – наиболее часто встречающееся значение ряда, другими словами, мода – это варианта, имеющая наибольшую частоту. В дискретных рядах мода определяется визуально, в интервальных рядах визуально определяется модальный интервал, а мода (точечная) определяется по формуле: , где
x? нижняя граница модального интервала;
i ?шаг интервального ряда;
fMо ?частота модального интервала;
fMо-1? частота интервала, предшествующего модальному;
fMо+1?частота интервала, следующего за модальным.
Пример: Найти Мо в дискретном и интервальном рядах.


.
2) Структурное среднее медиана (Mе) – значение, которое делит ранжированный ряд пополам.
В нечётных, чётных и дискретных рядах медиана определяется визуально, но в дискретных рядах она определяется с помощью накопленных частот. В интервальном ряду медианный интервал находится визуально, с помощью накопленных частот, а сама медиана (точечно) по формуле:

, где
x?нижняя граница медианного интервала;
i ?шаг интервального ряда;
?f ?сумма накопленных частот;
SMe-1?сумма частот, накопленных до медианного интервала;
fMe ?частота медианного интервала.
Пример: Найти Ме в нечетных, четных, дискретных, интервальных рядах.

интервальный ряд:

.
Если х сред. равно Мо = Ме – это симметричное распределение, если х сред не равно Мо, не равно Ме – распределение ассиметричное.
Источник
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
- Например, курс акций корпорации в основном определяется финансовыми результатами ее деятельности. В то же время, в отдельные дни и на отдельных биржах эти акции в силу сложившихся обстоятельств могут продаваться по более высокому или заниженному курсу.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
- средняя арифметическая;
- средняя гармоническая;
- средняя геометрическая;
- средняя квадратическая.
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
- Средняя арифметическая простая (невзвешенная) – вычисляется когда каждый вариант совокупности встречается только один раз.
- Средняя арифметическая (взвешенная) – варианты повторяются различное число раз, при этом число повторений вариантов называется частотой, или статистическим весом.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
- Средняя арифметическая простая – самый распространенный вид средней величины, рассчитывается по формуле (8.8):

(8.8 -формула средней арифметической простой)
- где хi – вариант, а n – количество единиц совокупности.
- Пример вычисления средней арифметической простой. Провели опрос о желаемом размере заработной платы у пяти сотрудников офиса. По результатам опроса выяснили, что желаемый размер заработной платы составляет соответственно для каждого сотрудника: 50000, 100000, 200000, 350000, 500000 рублей человек. Рассчитаем среднюю арифметическую простую по формуле (8.8):
 Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей.
Вывод: в среднем желаемый размер заработной платы по результатам опроса 5-ти человек составил 240 тысяч рублей. - Средняя арифметическая взвешенная формула 8.9.

(8.9 -формула средней арифметической взвешенной)
- где хi – вариант, а fi – частота или статистический вес.
- Пример вычисления средней арифметической взвешенной. Результаты опроса всех работников офиса приведены в табл. 8.2.
Таблица 8.2 – Результаты опроса работников офиса
Желаемый размер заработной платы, тыс.руб хi | Количество работников fi | хifi |
| 1 | 2 | 3 |
50 100 200 350 500 | 6 10 20 9 5 | 300 1000 4000 3150 2500 |
| Итого | 50 | 10950 |
Пример. Вычислим (ориентируясь на итоговые строки таблицы) желаемый размер заработной платы, 50 сотрудников офиса (используем формулу 8.9):

Пример вычисления средней арифметической взвешенной
Вывод: в среднем желаемый размер заработной платы по результатам опроса 50 человек составил 219 тысяч рублей.
Среднеарифметическая – всегда обобщающая количественная характеристика варьирующего признака совокупности.
- Средняя гармоническая вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины.
- Средняя гармоническая простая представлена ниже:

(8.10 – формула средней гармонической простой)
Средняя гармоническая взвешенная определяется по формуле

(8.11- формула средней гармонической взвешенной)
где xi – вариант, n – количество вариантов, Vi – веса для обратных значений xi.
Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, чем взвешенная. Для иллюстрации области ее применения воспользуемся упрощенным условным примером.
- Пример (вычисление средней гармонической простой (невзвешенной)).
Предположим, в фирме, специализирующейся на торговле по почте на основе предварительных заказов, упаковкой и отправкой товаров занимаются два работника. Первый из них на обработку одного заказа затрачивает 5 мин., второй – 15 мин.
- Каковы средние затраты времени на 1 заказ, если общая продолжительность рабочего времени у работников равна?
На первый взгляд, ответ на этот вопрос заключается в осреднении индивидуальных значений затрат времени на 1 заказ, т.е. если используем среднюю арифметическую простую получим: (5+15):2=10, мин.
- Проверим обоснованность такого подхода на примере одного часа (60 минут) работы. За этот час первый работник обрабатывает 12 заказов (60:5), второй – 4 заказа (60:15), что в сумме составляет 16 заказов.
Если же заменить индивидуальные значения их предполагаемым средним значением, то общее число обработанных обоими работниками заказов в данном случае уменьшится: (60/10) + (60/10) = 12 заказов (что не соответствует истине).
- Подойдем к решению через исходное соотношение средней. Для определения средних затрат времени необходимо общие затраты времени за любой интервал (например, за час) разделить на общее число обработанных за этот интервал двумя работниками заказов, т.е. используем среднюю гармоническую:

Пример вычисления средней гармонической простой (невзвешенной)
Если теперь мы заменим индивидуальные значения их средней величиной, то общее количество обработанных за час заказов не изменится: (60/7,5) + (60/7,5) = 16 заказов
- Подведем итог: средняя гармоническая невзвешенная может использоваться вместо взвешенной в тех случаях, когда значения Wj для единиц совокупности равны (в рассмотренном примере рабочий день у сотрудников одинаковый).
Пример (вычисление средней гармонической взвешенной) В ходе торгов на валютной бирже за первый час работы заключено пять сделок. Данные о сумме продажи рублей и курсе рубля по отношению к доллару США приведены в табл.8.3.
Таблица 8.3 – Данные о ходе торгов на валютной бирже (цифры условные)
Номер сделки Сумма продажи V, млн руб. Курс рубля x, руб. за 1 дол. V/x 1 2 3 4 1
2
3
4
5
455,00
327,50
528,00
266,00
332,50
65,00 65,50
66,00
66,50
66,50
7,00
5,00
8,00
4,00
5,00
итого 1909,00 – 29,00 Для того чтобы определить средний курс рубля по отношению к доллару, нужно найти соотношение между суммой продажи рублей, которые затрачены на покупку долларов в ходе всех сделок, и суммой приобретенных в результате этих сделок долларов.

- Вывод: средний курс за один доллар составил 65,83 руб.;
- Если бы для расчета среднего курса была использована средняя арифметическая простая:
 то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.
то, за один доллар, по данному курсу на покупку 29 млн дол. нужно было бы затратить 1899,5 млн.руб., что не соответствует действительности.Средняя геометрическая используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете средней геометрической индивидуальные значения признака обычно представляют собой относительные показатели динамики, построенные в виде цепных величин как отношение каждого уровня ряда к предыдущему уровню.
- Средняя геометрическая простая рассчитывается по формуле 8.12

(8.12)
- Если использовать частоты m, получим формулу средней геометрической взвешенной
- Средняя геометрическая взвешенная рассчитывается по формуле 8.13

(8.13)
Средняя квадратическая применяется, когда изучается вариация признака. В качестве вариантов используются отклонения фактических значений признака либо от средней арифметической, либо от заданной нормы.
Для несгруппированных данных используют формулу средней квадратической простой
Средняя квадратическая простая (формула 8.14)

8.14
Для сгруппированных данных используют формулу средней квадратической взвешенной
Средняя квадратическая взвешенная (формула 8.15)

(8.15) – Формула -средняя квадратическая взвешенная
Средние арифметическая, гармоническая, геометрическая и квадратическая, рассчитанные для одного и того же ряда вариантов, отличаются друг от друга. Их численное значение возрастает с ростом показателя степени в формуле степенной средней правило мажорантности средних А.Я. Боярского, т.е.

Мода и Медиана (структурные средние) формулы и примеры вычисления см. по ссылке
Источник
Средняя арифметическая величина обладает многими математическими свойствами, имеющими важное значение при ее расчёте. Знание этих свойств помогает контролировать правильность и точность расчёта средней варианты, способствует упрощению процесса расчёта среднего значения признака.
Первое свойство. Алгебраическая сумма отклонений индивидуальных вариант от среднего значения равна нулю. Так, если индивидуальные отклонения обозначить через ; …..; Сумма всех индивидуальных отклонений, например, в ранжированном ряду будет: Поскольку
Первое свойство теоретически доказывается и по отношению к средней арифметической взвешенной. В этом случае сумма взвешенных положительных отклонений от среднего значения признака равняется сумме взвешенных отрицательных отклонений, а общая сумма всех отклонений равна нулю, т.е. .
Первое свойство используется обычно для проверки правильности расчёта средней арифметической величины. В результате округления средней сумма отклонений не всегда равна нулю, но чем она ближе к нулю, тем средняя варианта рассчитана точнее.
Второе свойство. Величина средней не изменится, если частоты (частости) или веса при каждой варианте признака увеличить или уменьшить в одинаковое число раз.
Действительно, если то, например умножив все частоты на постоянную величину α, получим ту же величину средней:
.
Из второго свойства средней арифметической величины вытекают следующие важнейшие следствия:
· если частоты при всех вариантах равны между собой, то средняя арифметическая взвешенная равна простой средней, т.е. при равнозначности частот в вариационном ряду можно вычислить вместо взвешенной величины простую.
· при расчёте средней арифметической величины в качестве частот можно использовать частости, т.е. их удельные веса (доли) в общем итоге. Замену абсолютных частот частостями можно рассматривать как умножение их на некоторый коэффициент.
Третье свойство. Если все индивидуальные варианты вариационного ряда увеличить или уменьшить на постоянное число, то средняя величина увеличится или уменьшится на это же число. Обычно в качестве постоянного числа выбирается варианта, расположенная в середине вариационного ряда, что позволяет значительно упростить нахождение средней. Расчёт средней арифметической величины с применением этого свойства принято называть методом моментов. Метод моментов можно записать в следующем виде:
Четвёртое свойство. Произведение средней величины на накопленную сумму частот равняется сумме произведения каждой варианты на ее частоту, т.е.
Это свойство вытекает из формулы средней арифметической взвешенной величины, т.е. если
Применение основных свойств средней арифметической величины покажем на конкретном примере. Допустим, необходимо рассчитать среднею урожайность по группе зерновых и зернобобовых культур в сельскохозяйственной организации. Посевные площади, урожайность культур, а так же приемы применения второго и третьего свойств средней арифметической величины приведены в табл. 6.4.
Т а б л и ц а 6.4. Применение важнейших свойств при расчёте средней
Источник
1. Если все варианты
увеличить или уменьшить в несколько
раз, то средняя арифметическая увеличится
или уменьшится во столько же раз.
2. Если все варианты
увеличить или уменьшить на одно и то же
число, то средняя увеличится или
уменьшится на то же число.
3. Средняя
арифметическая суммы нескольких величин
равна сумме средних арифметических
этих величин.
4. Если все частоты
увеличить или уменьшить в несколько
раз, то средняя не изменится.
5. Алгебраическая
сумма отклонений значений признака от
средней арифметической всегда равна
нулю.
Пример:
имеется ряд распределения: 5, 10, 15, 20, 15.

Отклонения составят
следующие значения: –8, –3, 2, 7, 2.
Сумма отклонений
от средней величины равна нулю:
![]()
Свойства средней
арифметической применяются для упрощения
ее расчетов.
Пример:
определить средний размер вклада.
Таблица 4.5 –
Вспомогательная таблица для расчета
среднего размера вклада способом
моментов
Размер | Число | | x’–A* (A = 450) | i | f’= | |
200–300 | 50 | 250 | –200 | –2 | 5 | –10 |
300–400 | 60 | 350 | –100 | –1 | 6 | –6 |
400–500 | 40 | 450 | 4 | |||
500–600 | 30 | 550 | 100 | 1 | 3 | 3 |
600–700 | 50 | 650 | 200 | 2 | 5 | 10 |
Итого | 230 | – | – | – | 23 | –3 |


Данный способ
расчета средней арифметической взвешенной
называется способом моментов
(или способом
расчета от
условного нуля).
4.3. Средняя гармоническая простая и взвешенная
В ряде случаев
бывают известны варианты (х)
и произведение варианты на частоту
(х*f),
в то время как сами частоты неизвестны.
В этих случаях применяется средняя
гармоническая,
которая бывает взвешенной и простой.
1. Средняя
гармоническая взвешенная:
 –средняя
–средняя
арифметическая взвешенная.
 (4.5)
(4.5)
Пример: определить
среднюю заработную плату работников
по 3 корпусам пансионата.
Таблица 4.6 – Фонд
оплаты труда по корпусам пансионата


2. Средняя
гармоническая простая
Если произведение
f*x=M
равно 1, то для расчета средней величины
применяется средняя гармоническая
простая.
 (4.6)
(4.6)
 (4.7)
(4.7)
Пример:
в бригаде работает 3 человека, которые
оказывают одни и те же услуги
Таблица 4.7 –
Выработка сотрудников в бригаде
Затраты | Число услуг в | хf=М |
1/2 | 2 | 1 |
1/3 | 3 | 1 |
1/4 | 4 | 1 |
Затраты времени
на оказание одной услуги:
для 1-го работника
= 1/2 ч;
для 2-го работника
= 1/3 ч;
для 3-го работника
= 1/4 ч.
Определить средние
затраты времени на оказание услуги.

4.4. Средняя хронологическая
Средняя
хронологическая
применяется для расчета средней величины,
если исходные данные представлены на
определенные даты, моменты времени.
Пример:
определить среднюю стоимость имущества
пансионата за 1-й квартал по следующим
данным:
Таблица 4.8 Стоимость
имущества в 1 квартале
Дата | 01.01 | 01.02 | 01.03 | 01.04 |
Стоимость | 200 | 220 | 240 | 220 |



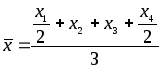 (4.8)
(4.8)
 (4.9)
(4.9)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
09.05.201520.38 Mб15Даниэльс, Олберти – Физическая химия, 1978.djvu
- #
- #
- #
Источник

