Какими свойствами обладают операции над событиями
1) ; | 2) ; | 3) ; |
4) ; | 5) ; | 6) ø; |
7) ; | 8) ; | 9) ; |
10) ; | 11) ; | 12) . |
Пример 1.1. Два шахматиста играют подряд две партии. Под исходом опыта будем понимать выигрыш одного из них в I-й партии или ничью. Построить пространство Элементарных исходов.
Решение. Обозначим события — в I-й партии выиграл первый игрок, — второй, С — ничья. Тогда возможные исходы игры:
1. Обе партии выиграл первый игрок .
2. Обе партии выиграл второй игрок .
3. Обе партии закончились вничью .
4. В первой партии выиграл первый игрок, во второй — второй .
5. В первой выиграл первый игрок, во второй — ничья .
6. В первой партии победа второго игрока, во второй — первого .
7. В первой — победа второго игрока, во второй — ничья .
8. В первой — ничья, во второй — победа первого игрока .
9. В первой — ничья, во второй — победа второго игрока .
Ответ: = , , , , , , , , .
Пример 1.2. Пусть А, В, С — три произвольных события. Найти выражения для событий, состоящих в том, что из А, В, С:
1. Произошло только А.
2. Произошло А и В, но С не произошло.
3. Все три события произошли.
4. Произошло, по крайней мере, одно из событий.
5. Произошли, по крайней мере, два события.
6. Произошло одно и только одно событие.
7. Произошли два и только два события.
8. Ни одно событие не произошло.
9. Произошло не более двух событий.
Решение.
1. Обозначим и , что события В и С не произошли, тогда событие: произошло только А можно записать в виде .
2.
3.
4. Событие произошло, по крайней мере, одно из событий можно представить как сумму этих событий: А + В + С.
5. Произошли, по крайней мере, два события — это сумма АВ + АС + ВС.
6. Произошло одно и только одно событие — это сумма событий
7. Произошли два и только два события — можно записать в виде , или АВ + АС + ВС – АВС.
8.
9. , т. е. три события одновременно не произошли.
Пример 1.3. События А, В и С означают, что взято хотя бы по одной книге из трех различных собраний сочинений, каждое из которых содержит по крайней мере три тома. События И Означают соответственно, что из первого собрания сочинений взяты S, а из второго K томов. Что означают события: а) А +
+ В + С; б) АВС; в) ; г) ; д) ?
Решение.
1. А + В + С — взята хотя бы одна книга.
2. АВС — взято хотя бы по одному тому из первого, второго и третьего со – брания сочинений.
3. — взята одна книга из первого собрания сочинений или три книги из второго собрания сочинений, или одна из первого и три из второго собрания сочинений одновременно.
4. — взято по два тома из первого и второго собрания сочинений.
5. — взят хотя бы один том из третьего собрания сочинений и один том из первого и три тома из второго собрания сочинений или три тома из первого и один том из второго собрания сочинений.
Пример 1.4. Пусть – события: Ваша встреча с I-ым другом. Составьте события: а) с друзьями Вы не встречались; б) Вы встречались только со вторым другом; в) с кем-то Вы не встретились; г) Вы встретились с большей частью друзей; д) у Вас состоялась встреча только с одним другом; е) Вы встретились с кем-то из первых двух друзей, а с третьим другом – нет; ж) со вторым другом Вы не встретились.
Назовите события: а) ; б) ; в) ; г) ;
д) ; е) ; ж) .
Решение. Составим события:
А) Так как событие – «Ваша встреча с I-ым другом», то – «с I-ым другом Вы не встретились». Поэтому событие «с друзьями Вы не встречались» – это совместное наступление событий , т. е. .
Б) Слово Только говорит о том, что с первым и вторым другом Вы не встречались, а со вторым – да. Это .
В) Этот кто-то может быть любым из ваших друзей, поэтому событие – сумма событий , т. е. .
Г) Так как друзей трое, а большая часть – это более половины, то Вы встретились, по крайней мере, с двумя друзьями, поэтому событие – сумма событий и , т. е. .
Д) Этим одним другом может быть любой из Ваших трех друзей, поэтому это событие есть сумма таких событий: «Вы встретились только с первым другом» или «встретились только со вторым», или «встретились только с третьим», т. е. .
Е) Встреча с кем-то из первых двух друзей – это встреча либо с первым другом, либо со вторым (а может быть и с обоими), т. е. это сумма и в то же время не встретились с третьим. Поэтому ответ: .
Ж) Так как – «встреча со вторым другом», то – «встречи со вторым другом не было». Так как про других друзей ничего не говорится, то не надо думать про встречи с ними.
Назовем события:
А) Вы не встретились только с одним другом (или Вы встретились только с двумя).
Б) Событие – «ни с кем Вы не встретились», а событие – противоположное событию (отрицание этого события). Поэтому ответ: встречи были (с кем-то Вы встретились). Итак, .
В) С двумя друзьями Вы не встречались (с большей частью своих друзей Вы не встречались).
Г) С первым другом Вы встретились, а с кем-то из остальных – нет.
Д) Вы не встретились только со вторым другом (или у Вас была встреча только с первым и третьим другом).
Е) Так как событие «Вы с кем-то встречались», то событие – ему противоположное (отрицание этого события – «Вы ни с кем не встречались», т. е. . Итак, .
Источник
Некоторые свойства
операций над событиями постулируются,
другие легко могут быть получены с
помощью диаграмм Венна. Приведем без
доказательства основные из этих свойств.
Алгебра и сигма-алгебра событий.
Пусть
![]() является пространством всех элементарных
является пространством всех элементарных
исходов для какого-нибудь случайного
эксперимента, каждому результату
которого соответствует ровно одна точка![]() .
.
Выделим совокупность подмножеств![]() множества
множества![]() .
.
При этом потребуем, чтобы![]() содержало как случайные события
содержало как случайные события![]() ,
,
так и события, полученные в результате
применения любой из описанных операций
к любым элементам системы.
Совокупность
![]() случайных событий
случайных событий![]() (подмножеств множества
(подмножеств множества![]() ),
),
определенных на пространстве элементарных
исходов![]() ,
,
называетсяалгеброй событий (илибулевой алгеброй– по имени
английского математика Дж. Буля (1815 –
1864)), если выполнены следующие условия:
 ;
;Если
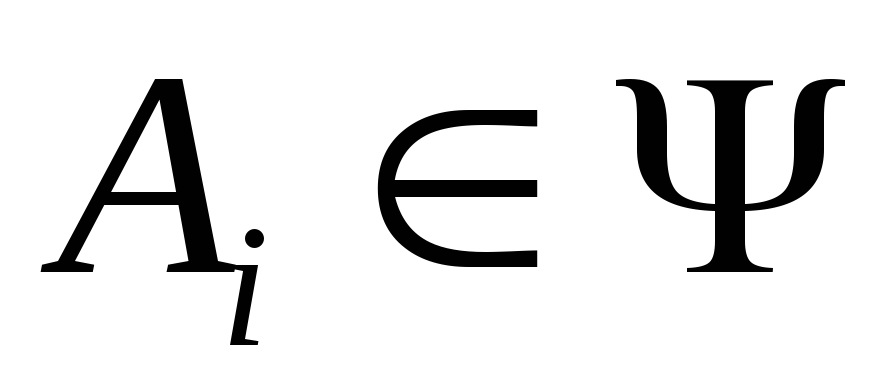 и
и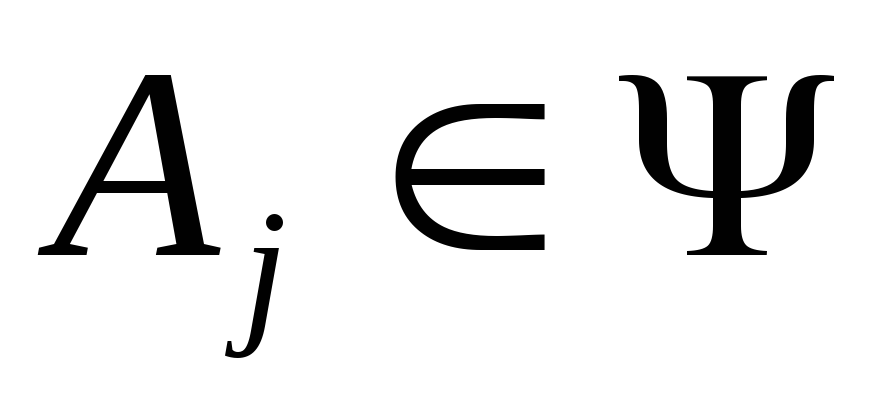 ,
,
то для
для
любых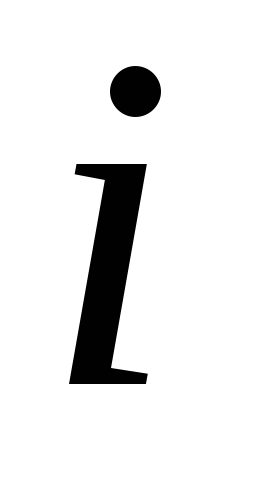 и
и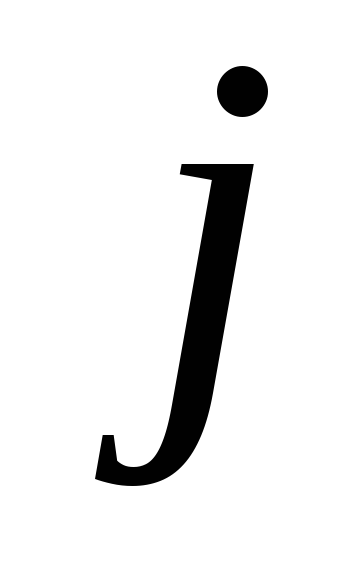 ;
;Если
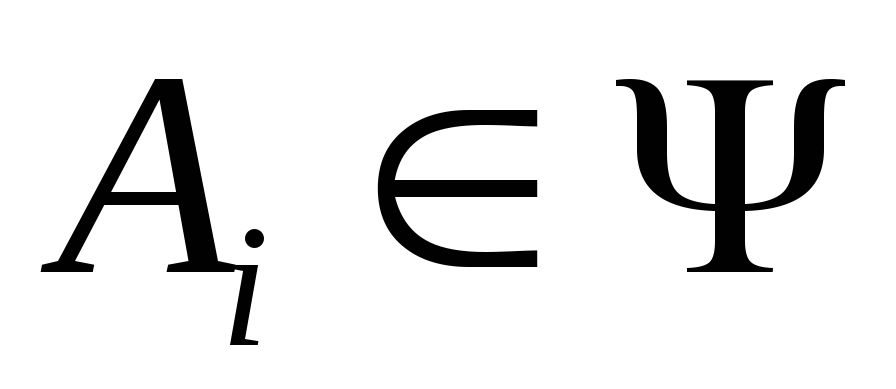 ,
,
то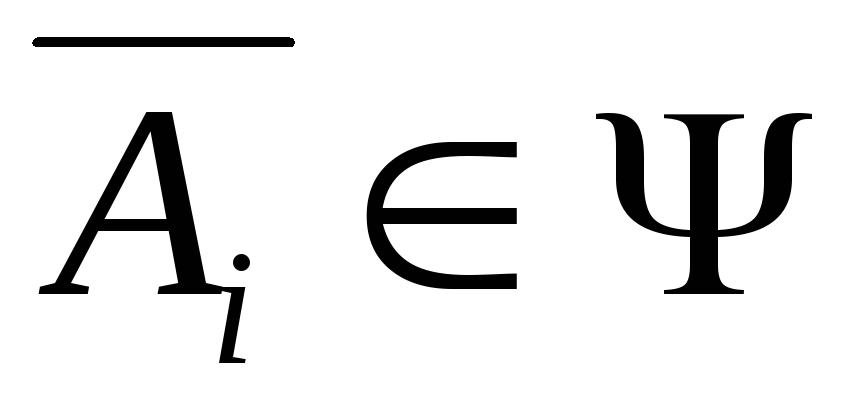 .
.
Оказывается, что
условий 1 – 3 достаточно для того, чтобы
любое конечное число других операций
над случайными событиями
![]() не выводило бы нас за пределы алгебры
не выводило бы нас за пределы алгебры![]() .
.
Для экспериментовс конечным числом
исходов множество всех подмножеств![]() ,
,
включающее пустое множество,
составляет алгебру. Поэтому для таких
экспериментов любое подмножество
множества![]() может интерпретироваться как наблюдаемое
может интерпретироваться как наблюдаемое
событие.
Во многих задачах
теории вероятностей приходится иметь
дело и с бесконечным числом элементарных
исходов и, следовательно, операций. Это
потребовало введения понятия -алгебры
событий.
Система подмножеств
![]() множества, называется-алгеброй,
множества, называется-алгеброй,
если она удовлетворяет следующим
условиям:
 ;
;Если
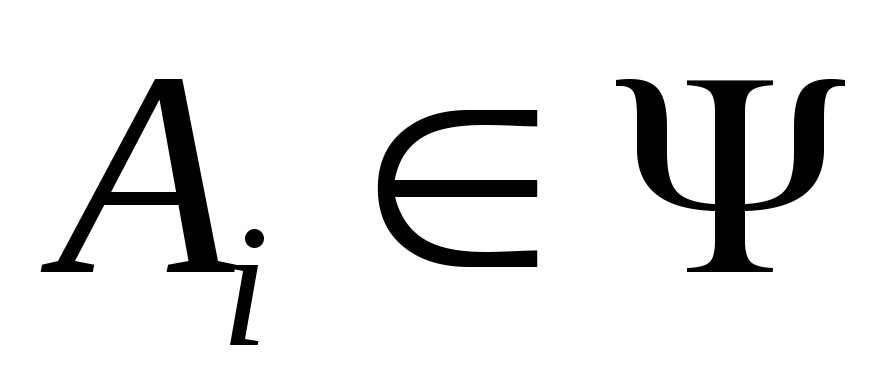 , то
, то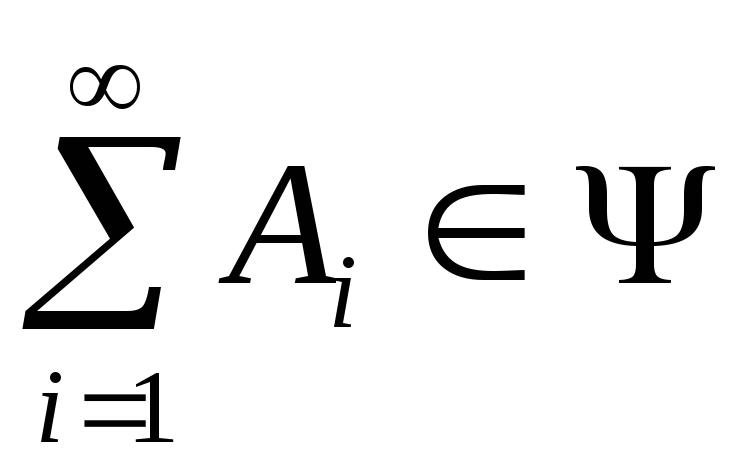 и
и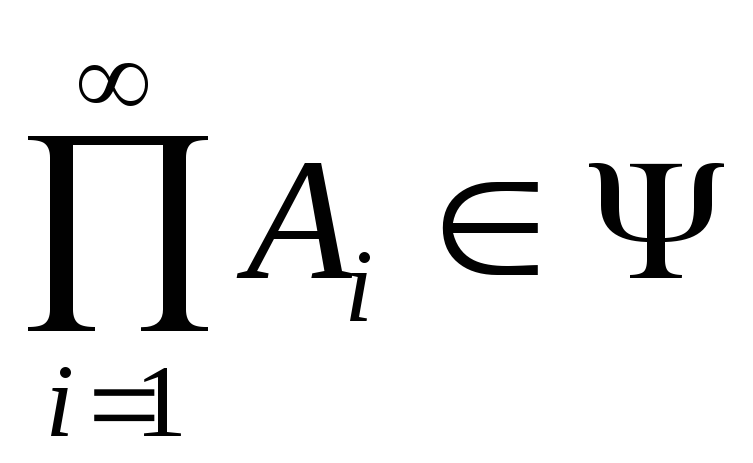
Если
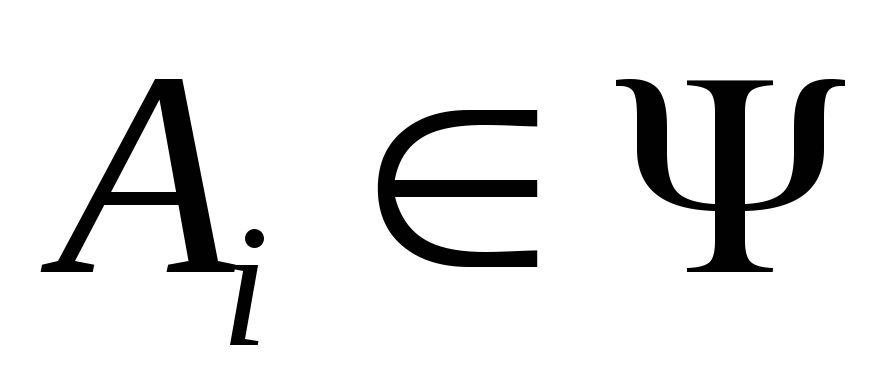 ,
,
то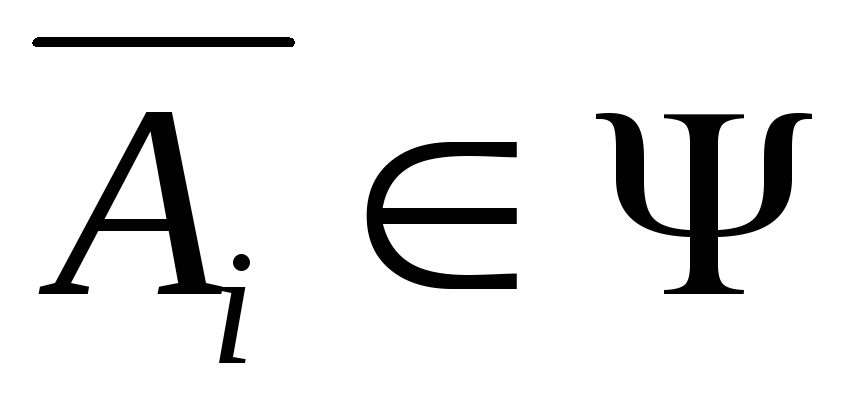 .
.
Таким образом,
счетное число операций суммирования
или перемножения событий не выводит
результирующее событие за пределы
–алгебры.
Лекция 3.
Классическое определение вероятности
события. Статистическое определение
вероятности. Геометрические вероятности.
Аксиоматическое построение теории
вероятностей. Вероятностное пространство.
Вероятностьявляется количественной мерой возможности
появления события. Наиболее широкое
распространение получили два определения
вероятности события: классическое и
статистическое.
Классическое определение вероятности события. Случаи равновероятных исходов.
Классическое
определение вероятностисвязано с
определением благоприятствующего
исхода. Исход называется благоприятствующим
данному событию, если его появление
влечет за собой наступление этого
события.Вероятность события равна
отношению числа равновозможных
благоприятствующих элементарных исходов
к общему числу всех равновозможных
элементарных исходов данного испытания:
![]() ,
,
где ![]() –
–
число благоприятствующих событию![]() исходов;
исходов;
![]() – общее число возможных исходов.
– общее число возможных исходов.
Примеры:1. Кубик,
2. Какова вероятность того, что в
произвольном двузначном числе две цифры
одинаковы (9/90 = 0.1), 3. Из букв слова
“дифференциал” выбирается одна буква.
Какова вероятность того, что это а)
гласная, б) буква “ф”.
Из определения
вероятности события
![]() следует, что
следует, что![]() ,
,
поэтому всегда выполняются неравенства![]() ,
,
т.е.вероятность любого события есть
неотрицательное число, не превышающее
единицы.
Если
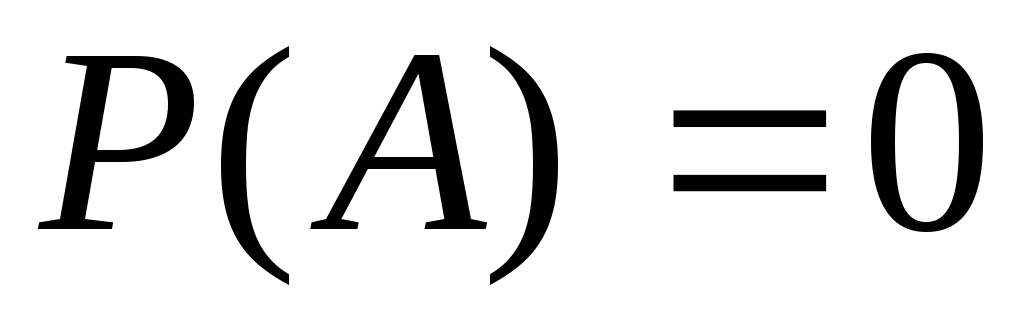 ,
,
то событие невозможное.
невозможное.Если
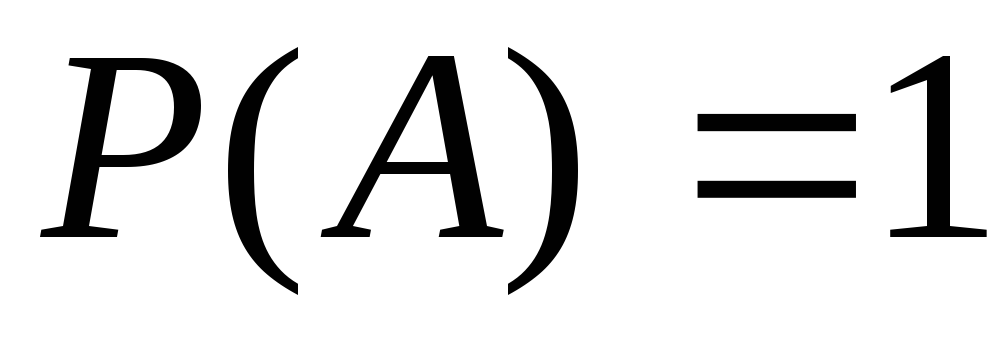 ,
,
то событие достоверное.
достоверное.Равновозможные
элементарные события являются
равновероятными, т.е. обладают одной
и той же вероятностью.
Теорема.
Эквивалентные события имеют
одинаковые вероятности, т.е. если
![]() ,
,
то![]() .
.
Доказательство.
Действительно, каждый элементарный
исход события![]() является таким же элементарным исходом
является таким же элементарным исходом
для события![]() и наоборот. В силу формулы
и наоборот. В силу формулы![]() справедливо равенство
справедливо равенство
![]() .
.
Если событие
![]() происходит всякий раз после того, как
происходит всякий раз после того, как
произошло событие![]() ,
,
то говорят, что из события![]() следует событие
следует событие![]() (
(![]() ).
).
Например, для любых двух событий![]() и
и![]() справедливо
справедливо![]() и
и![]() .
.
Теорема. Если
![]() ,
,
то![]() .
.
Доказательство.
Пусть![]() и
и![]() – число благоприятных элементарных
– число благоприятных элементарных
исходов соответственно для событий![]() и
и![]() ,
,
а![]() – общее число элементарных исходов.
– общее число элементарных исходов.
Так как каждый элементарный исход для
события![]() является также элементарным исходом
является также элементарным исходом
для события![]() ,
,
то![]() и, следовательно,
и, следовательно,![]() .Пример: выпадение четного числа
.Пример: выпадение четного числа
очков более вероятно, чем выпадение
двойки.
Теорема. Вероятность
события ![]() ,
,
противоположного событию ![]()
равна
![]() .
.
Доказательство.
Пусть полная система равновозможных
элементарных исходов содержит![]() событий, из которых
событий, из которых![]() (
(![]() ),
),
благоприятны событию![]() .
.
Тогда![]() исходов неблагоприятны событию
исходов неблагоприятны событию![]() ,
,
т.е. благоприятствуют событию![]() .
.
Таким образом,
![]() .
.
Классическое
определение вероятности предполагает,
что
число элементарных
исходов конечно;эти исходы
равновозможны.
Однако на практике
встречаются испытания с бесконечным
числом возможных исходов. Кроме того,
нет общих методов, позволяющих результат
испытания, даже с конечным числом
исходов, представить в виде суммы
равновозможных элементарных исходов.
Поэтому применение классического
определения вероятности весьма
ограничено. Пример: кубик со
смещенным центром тяжести.
Источник
1. Переместительный закон
А + В = В + А,
А·В = В·А.
2. Распределительный закон
(А + В)·С = А·С + В·С,
А·В + С = (А + С)·(В + С).
3. Сочетательный закон
(А + В) + С = А + (В + С),
(А·В)·С = А·(В·С).
4. Закон «тождественности»
А + А = А,
А·А = А.
5. Закон «полноты»
А + = ,
А· = А.
6. Закон «дополнения»
А + Ᾱ = ,
А·Ᾱ = Ø.
7. Законы «отрицания»
«не Ø» = Ω,
= Ø,
8. Закон «разности»
А – В = А· .
9. Законы де Моргана
= · ,
= + .
Задачи, рассмотренные на лекции и семинаре. Тема 1.
События. Основные операции над событиями
Лекция 1
Задача 1-Т1. Из таблицы случайных чисел наудачу взято одно число. Введем события: А = {выбранное число делится на 5}, В = {выбранное число оканчивается нулем}. Выяснить смысл событий
а) ;
б) .
Задача 2-Т1. Какие из следующих пар событий являются несовместными? совместными?
а) А1 = {выход из строя телевизора, работающего в гостиной} и А2 = {на кухне}?
б) А3 = {попадание при одном выстреле}, А4 = {промах};
в) А5 = {выпадение герба при подбрасывании монеты}, А6 = {выпадение решки};
г) А7 = {хотя бы одно попадание при двух выстрелах}, А8 = {два попадания}.
Задача 3-Т1 для самостоятельного решения. Из четырех карточек с номерами 1, 2, 3, 4 последовательно наудачу берут две. Составить пространство элементарных событий для этого опыта, если его элементами служат:
а) двузначные числа, образованные этими карточками?
б) суммы номеров, изображенных на извлеченных карточка?
Задача 4-Т1. Доказать формулу А + В = А + ·В, где А и В – случайные события.
Задача 5-Т1. В лаборатории работают несколько человек, причем каждый из работников знает хотя бы один иностранный язык. Так,
– английский знают 6 человек,
– немецкий – 6 человек,
– французский – 7 человек,
– английский и немецкий – 4 человека,
– немецкий и французский – 3 человека,
– английский и французский – 2 человека,
– все три языка знает один человек.
Сколько человек работает в лаборатории? Сколько сотрудников знают только английский язык?
Семинар 1
Задача 1С-Т1. Два шахматиста играют одну партию. Вводятся события: А = {выигрывает первый игрок}, B = {выигрывает второй игрок}. Описать события:
а) ;
б) ;
в) .
Задача 2С-Т1. Упростить выражение (А + В) ·(А + ) ·(Ᾱ+В).
Задача 3С-Т1. Упростить выражения:
а) А·(В – А·В);
б) А· + А··С + В·С + В;
в) А + Ᾱ·В + («не (А + В)»).
Задача 4С-Т1. Доказать справедливость законов де Моргана:
а) ;
б) .
Задача 5С-Т1. Упростить выражения, если известно, что А В:
а) А·В;
б) А + В;
с) А + В + С.
Задача 6С-Т1. Установите, какие из соотношений правильны:
а) Ᾱ + = ;
б) ;
в) (А + В) – С = А + (В – С).
Задача 7С-Т1. Совместны ли события А и ?
Задача 8С-Т1. Справедливы ли, а если «Да», то в каком случае равенства:
а) А·В = Ᾱ?
б) А + В = Ᾱ?
Задача 9С-Т1. Назвать противоположные события для следующих событий:
а) А = {выигрыш первого игрока в шахматной партии};
б) В = {произошло хотя бы одно попадание при десяти выстрелах};
в) С = {произошло три попадания при трех выстрелах};
г) D = {произошло не более двух попаданий при пяти выстрелах};
д) Е = {в семейной паре муж старше жены}.
Задача 10С-Т1. Известно, что события А1 и А2 произошли, а событие А3 не произошло. Произошли ли события:
а) ?
б) А1 + А2 ·А3?
в) А1 ·А2 ·А3?
Задача 11С-Т1. Каков смысл равенств:
а) А·В·С = А?
б) А + В + С = А?
Задача 12С-Т1. При каком условии справедливо равенство (А + В) – В = А – В?.
Задача 13С-Т1. Студент пришел на зачет, зная 15 вопросов из 20. Если студент не может ответить на вопрос, ему предоставляется еще одна (не более!) попытка. Каково пространство исходов?
Запишите событие А = {студент сдал зачет} через возможные исходы испытания.
Какова вероятность сдать зачет?
Домашнее задание 1 – Тема 1.
Задача 0Д-Т1. Перечислить все элементарные равновозможные события, которые могут произойти в результате:
а) подбрасывания монеты;
б) подбрасывания игрального кубика;
в) подбрасывания тетраэдра с гранями, занумерованными числами 1, 2, 3, 4;
г) раскручивания рулетки, поверхность которой разделена на 5 секторов, обозначенных буквами А, В, С, D, Е.
Задача 1Д-Т1. Одновременно подбрасываются 4 монеты. Вводятся события:
– А = {гербов выпало больше, чем цифр},
– В = {выпали все гербы},
– С = {выпали все цифры}. Объяснить смысл событий:
а)
б)
в)
г)
д)
е)
Задача 2Д-Т1. Двухмоторный самолет терпит аварию, если одновременно отказывают оба двигателя или выходит из строя система управления. Вводятся события:
– А ={выходит из строя k-двигатель}, k=1, 2;
– В = {выходит из строя система управления},
– С = {самолет терпит аварию}. Описать события , .
Задача 3Д-Т1. Доказать формулы:
1) В = А·В + Ᾱ·В.
2) (А+С)·(В+С) = А·В+С.
Задача 4Д-Т1. Пусть А, В и С – три произвольных события. Выразить их через следующие события:
а) произошли все три события;
б) произошло только С;
в) произошло хотя бы одно из событий;
г) ни одного события не произошло;
д) произошли события А и В, но С не произошло;
е) произошло одно из этих событий;
ж) произошло не более двух событий.
Задача 5Д-Т1. Событие А влечет за собой В. Что представляют собой события:
а) А + В?
б) А·В?
в) А – В?
г)
Задача 6Д-Т1. Пусть событие А = {экзамен сдан}, а событие В = {экзамен сдан на «отлично»}. В чем состоят события:
а) А – В?
б) «не (А – В)» = ?
в) ?
Задача 7Д-Т1. Три студента независимо друг от друга решают одну и ту же задачу. Пусть события:
А1 = {первый студент решил задачу},
А2 = {второй студент решил задачу},
А3 = {третий студент решил задачу}.
Выразить через события следующие события:
1) А = {все студенты решили задачу},
2) В = {задачу решил только первый студент},
3) С = {задачу решил хотя бы один студент},
4) D = {задачу решил только один студент}.
Задача 8Д-Т1. Из корзины, содержащей красные, желтые и белые розы, выбирается один цветок. Пусть события:
– А = {выбрана красная роза},
– В = {выбрана желтая роза},
– С = {выбрана белая роза}.
Что означают события:
а) ,
б) А + В,
в) А·С,
г) ,
д) ,
е) А·В + С.
Задача 9Д-Т1. Указать пространство элементарных событий для следующего испытания (опыта) – одновременное подбрасывание двух костей.
Задача 10Д-Т1. В урне находятся 12 пронумерованных шаров. Опыт состоит в извлечении одного шара из урны. Требуется:
1) составить пространство элементарных событий для данного опыта;
2) указать элементарные исходы (события), благоприятствующие событиям:
А = {появление шара с нечетным номером},
В = {появление шара с четным номером},
С = {появление шара с номером, большим трех},
D = {появление шара с номером, меньшим 7};
3) пояснить, что означают события «не В», «не С»;
4) указать, какие из пар А, В, С, D совместны, а какие – нет;
5) привести примеры невозможного и достоверного событий;
7) привести пример другого пространства элементарных событий в данном опыте.
Задача 11Д-Т1. На загородную прогулку поехали 92 человека. Бутерброды с колбасой взяли 47 человек, с сыром – 38 человек, с ветчиной – 42 человека, с сыром и колбасой – 28 человек, с колбасой и ветчиной – 31 человек, с сыром и ветчиной – 26 человек, все три вида бутербродов взяли 25 человек. Несколько человек вместо бутербродов захватили с собой пирожки. Сколько человек взяли с собой пирожки?
Задача 12Д-Т1. Из событий а) «идет дождь», б) «на небе нет ни облачка», в) «наступила осень» составить все возможные пары и выявить среди них все пары совместных событий и несовместных событий.
Задача 13Д-Т1. Имеется правильная трехгранная пирамида – тетраэдр. Одна из ее граней серая, остальные – белые. Тетраэдр бросают на стол и наблюдают за гранью, которой он соприкасается с поверхностью стола. Являются ли равновозможными события «тетраэдр упал на серую грань» и «тетраэдр упал на белую грань»?
Задача 14Д-Т1. Из полной колоды карт (36 штук) вынимается одна карта. Являются ли равновозможными события: а) «вынута карта черной масти» и «вынута карта красной масти»? б) «вынут Король» и «вынута Дама»? в) «вынута карта бубновой масти» и «вынута карта червонной масти»? г) «вынута карта пиковой масти» и «вынута карта красной масти»? д) «вынута шестерка треф» и «вынута Дама пик»?
Задача 15Д-Т1. Из полной колоды карт вынимается одна карта. Выяснить, являются ли совместными события:
а) «вынута карта красной масти» и «вынут Валет»;
б) «вынут Король» и «вынут Валет»?
Тема 2. Частость (частота) события. Свойство статистической устойчивости относительной частоты события. Статистическое определение вероятности. Элементы комбинаторики – 4 часа: 2 часа лекции, 2 часа семинарское занятие
Источник
ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
Теория вероятностей – математическая наука, изучающая закономерности случайных явлений.
Случайное явление – явление, которое при неоднократном воспроизведении одного и того же опыта (при неоднократных испытаниях) протекает каждый раз несколько по-иному.
Опыт (испытание) – всякое осуществление определённого комплекса условий или действий, при которых происходит соответствующее явление.
Событие – возможный результат опыта.
Случайное событие – событие, которое при осуществлении данного опыта может наступить, а может и не наступить.
Достоверное событие (U) – событие, которое при осуществлении данного опыта всегда наступит.
Невозможное событие (V) – событие, которое при осуществлении данного опыта никогда наступит.
Равновозможные события – события,для которых при осуществлении данного опыта нет оснований считать, что возможность появления одного из них больше, чем другого.
Несовместные события – события, которые при осуществлении данного опыта не могут наступить одновременно (появление одного из них исключает появление других в одном и том же опыте).
Полная группа событий (совокупность единственно возможных событий) – группа таких событий, для которых выполняется: в результате данного опыта обязательно происходит и только одно из них.
Противоположные события – события А и , для которых выполняется: в результате данного опыта наступление А равносильно тому, что не наступит.
Элементарные исходы (случаи, шансы) – равновозможные, несовместные события, образующие полную группу событий.
Пространство элементарных исходов – совокупность элементарных исходов . Часто используют обозначение: . Любой результат эксперимента (событие) – это точка пространства . Если можно считать, что ни один из элементарных исходов (случаев) не является предпочтительным, т.е. исходы равновозможны, каждому элементарному исходу можно приписать число . Это число называют вероятностью данного случая. Таким образом, для нахождения вероятности необходимо найти число элементарных исходов.
Благоприятные (благоприятствующие) случаи (для события) – случаи, при которых данное событие наступает. Появление благоприятного случая является проявлением данного события.
Классическое определение вероятности
Пусть m – число элементарных исходов, благоприятствующих событию А, n – число всех равновозможных элементарных исходов опыта, в котором может появиться это событие. Вероятностью события А называется отношение m/n:
Р(А) = m/n.(1)
Свойства вероятности
· для достоверного события U выполняется: Р(U) = 1;
· для невозможного события V: Р(V) = 0;
· для случайного события A: 0 < P(A) < 1;
· для любого события В: 0 ≤ Р(В) ≤ 1.
Комбинаторика – раздел математики, изучающий количества комбинаций, подчиняющихся определённым условиям, которые можно составить из элементов заданного конечного множества.
Правило суммы
Если некоторый объект А может быть выбран из совокупности объектов m способами, а В – другими k способами, то выбрать объект А+В (А или В) можно m+k способами.
Правило произведения
Если объект А может быть выбран из совокупности объектов m способами, а после каждого такого выбора объект В может быть выбран k способами, то выбор упорядоченной пары АВ (А∙В, А и В) может быть произведён m∙k способами.
Размещения – комбинации, составленные из n различных элементов по m элементов (m ≤ n), которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений :
. (2)
Перестановки – комбинации, составленные из n различных элементов по n элементов, отличающихся только порядком их расположения. Число всех возможных перестановок :
. (3)
Сочетания – комбинации, составленные из данных n различных элементов по m элементов (m ≤ n), которые отличаются хотя бы одним элементом. Число сочетаний :
. (2)
Перестановки с повторениями – комбинации, составленные из данных n элементов, среди которых n1 элементов одного вида, n2 элементов другого вида и т.д.: n1 + n2 + …+ nk = n. Число перестановок с повторениями можно подсчитать по формуле:
. (5)
Размещения с повторениями – комбинации, составленные из n различных элементов по m элементов (элементы в таких комбинациях могут повторяться, при этом может оказаться, что n ≤ m). Число размещений с повторениями находят по формуле:
. (6)
Сочетания с повторениями – комбинации, составленных из n различных элементов по m элементов, элементы в которых могут повторяться, но в отличие от числа размещений с повторениями, последовательность при выборе элементов не важна. Число таких комбинаций находят по формуле:
. (7)
Геометрическая вероятность – обобщение классической вероятностной модели с конечным или счётным числом равновероятных элементарных исходов. Пусть пространству элементарных исходов соответствует некоторый выделенный объём (площадь или длина ); а событию А соответствует некоторая область с объёмом (площадью или длиной ). Тогда вероятностью события А можно считать отношение:
. (3)
Статистическая вероятность – число, близкое к m/n при неограниченном возрастании n – числа независимых испытаний, если m – число появлений события А в этой серии из n испытаний. Величина m/n называется относительной частотой события А (или частостью). При этом справедлива теорема Бернулли (частный случай теоремы Чебышева – одного из законов больших чисел [1, с. 97]). Согласно этой теореме, в описанной ситуации для любого положительного числа предел вероятности события равен 1:
.
Предел, используемый в теореме Чебышева, называют пределом по вероятности. Таким образом, практически достоверным при больших значениях n является событие: вероятность р события А сколь угодно близка к его относительной частоте m/n.
Сумма или объединение событий – событие, состоящее в появлении хотя бы одного из них.
Произведение (пересечение) событий – событие, состоящее в одновременном появлении этих событий.
Сумму трёх событий (А1, А2, А3) можно рассмотреть как сумму события (А1+А2) и события А3; аналогично для четырёх, пяти событий и так далее (так же и произведение нескольких событий).
Обобщая понятия, связанные с действиями над событиями, на множестве событий вводят алгебраические операции (используя символику действий над множествами):
· объединение (сумма) двух событий А и В – событие С, такое, что ;
· дополнение (противоположное событию А) – событие , такое, что ;
· пересечение (произведение) двух событий А и В – событие С, такое, что ;
· следствие (из А следует В, А включается в В, А влечёт В):;
· невозможное событие ;
· достоверное событие ;
· разность двух событий А и В – событие С, такое, что ;
· симметрическая разность двух событий А и В – событие С, такое, что
Алгебра событий
Множество событий S называется алгеброй событий, если выполняются следующие условия (аксиомы событий):
1. ;
2.
Припишем каждому элементарному событию (исходу) некоторый «вес» – вероятность исхода . Совокупность вероятностей должна удовлетворять условиям:
1. ,
2. .
В этом случае вероятность некоторого события А определяется формулой: . При этом тройка , где , а S – некоторая алгебра подмножеств [2, с. 54], определяет вероятностную модель, или вероятностное пространство, обладающее свойствами:
1. ,
2. ,
3. ,
4. ,
5. .
Свойства действий над событиями
1. – коммутативность;
2.
– ассоциативность;
3. – дистрибутивность;
4. ;
5. ;
6. ;
7. ;
8. ;
9. ;
10. .
Читайте также:
Рекомендуемые страницы:
©2015-2020 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2016-02-12
Нарушение авторских прав и Нарушение персональных данных
Источник
