Какими свойствами обладают линзы

Линза (оптическая) – прозрачное тело, ограниченное двумя сферическими или одной сферической и другой плоской поверхностями. Линзы бывают также параболическими, цилиндрическими и другими криволинейными поверхностями.
Сферические поверхности линз могут иметь различную кривизну (различную степень выпуклости или вогнутости), отстоять одна от другой на различном расстоянии и могут быть обращены в одну сторону или в противоположные.
Все это приводит к большому разнообразию линз, однако разнообразие это может быть сведено к шести типам, показанным в разрезе на иллюстрации.
Типы сферических линз
Первые три линзы называются выпуклыми, или положительными (1, 2 и 3). Они в центре толще, чем по краям. Следующие три называются вогнутыми, или отрицательными (4, 5 и 6), и отличаются от первых тем, что они в центре тоньше, чем по краям.

На иллюстрации:
- 1) двояковыпуклая;
- 2) плоско-выпуклая;
- 3) вогнуто-выпуклая;
- 4) двояковогнутая;
- 5) плоско-вогнутая;
- 6) выгнуто-вогнутая.
На рисунке приведены элементы двояковыпуклой линзы. C1 и C2 – центры ограничивающих сферических поверхностей, называемые центрами кривизны; R1 и R2 – радиусы сферических поверхностей, называемые радиусами кривизны. Прямая, соединяющая центры кривизны C1 и C2, называется главной оптической осью. Для плоско-выпуклой или плоско-вогнутой линзы главной оптической осью является прямая, проходящая через центр кривизны перпендикулярно к плоской поверхности линзы. Точки пересечения главной оптической оси с поверхностью А и Б называются вершинами линзы. Расстояние между вершинами АБ называется осевой толщиной.
Свойства линз
Наиважнейшей особенностью положительных линз является способность давать изображение предметов. Действие положительных линз состоит в том, что они собирают падающие лучи, поэтому их называют собирательными.
Это свойство объясняется тем, что собирательная линза представляет собой совокупность множества трехгранных призм, расположенных по кругу и обращенных к центру круга своими основаниями. Поскольку такие призмы отклоняют падающие на них лучи к своим основаниям, пучок лучей, падающий на всю поверхность собирательной линзы, собирается в направлении к оси круга, т.е. к оптической оси.

Если из светящейся точки S, лежащей на оптической оси собирательной линзы, направить пучок расходящихся лучей света, то расходящийся пучок превратится в сходящийся, и в точке схода лучей образуется действительное изображение S` светящейся точки S. Поместив в точке S` какой-либо экран, можно увидеть на нем изображение светящейся точки S. Его называют действительным изображением.
 Образование действительного изображения светящейся точки. S` – действительное изображение точки S
Образование действительного изображения светящейся точки. S` – действительное изображение точки S
Отрицательные линзы, в противоположность положительным, рассеивают падающие на них лучи. Поэтому они называются рассеивающими.
 Действие рассеивающей линзы
Действие рассеивающей линзы
Если такой же пучок расходящихся лучей направить на рассеивающую линзу, то, пройдя сквозь нее, лучи отклоняются в стороны от оптической оси. Вследствие этого рассеивающие линзы не дают действительного изображения. В оптических системах, дающих действительное изображение, и, в частности, в фотообъективах рассеивающие линзы применяются только совместно с собирательными.
Фокус и фокусное расстояние
Если из точки, лежащей в бесконечности на главной оптической оси, направить на линзу пучок света (такие лучи можно считать практически параллельными), то лучи соберутся в одной точке F, лежащей также на главной оптической оси. Эта точка называется главным фокусом, расстояние f от линзы до этой точки – главным фокусным расстоянием, а плоскость MN, проходящая через главный фокус перпендикулярно оптической оси линзы, – главной фокальной плоскостью.
 Главный фокус F и главное фокусное расстояние f линзы
Главный фокус F и главное фокусное расстояние f линзы
Фокусное расстояние линзы зависит от кривизны ее выпуклых поверхностей. Чем меньше радиусы кривизны, т.е. чем выпуклее стекло, тем короче ее фокусное расстояние.
Оптическая сила линзы
Оптической силой линзы называется ее преломляющая способность (способность сильнее или слабее отклонять лучи света). Чем больше фокусное расстояние, тем меньше преломляющая способность. Оптическая сила линзы обратно пропорциональна фокусному расстоянию.
Единицей измерения оптической силы является диоптрия, обозначаемая буквой D. Выражение оптической силы в диоптриях удобно тем, что, во-первых, оно позволяет по знаку определить, с какой линзой (собирательной или рассеивающей) имеют дело и, во-вторых, тем, что позволяет легко определить оптическую силу системы из двух и большего числа линз.
Образование картинки
Падая на предмет, лучи света отражаются от каждой точки его поверхности во всех возможных направлениях. Если перед освещенным предметом поместить собирательную линзу, то от каждой точки предмета на линзу упадет конический пучок лучей.
 Схема образования действительного изображения
Схема образования действительного изображения
Пройдя через линзу, лучи снова соберутся в одну точку, и в месте схода лучей возникнет действительное изображение взятой точки предмета, а совокупность изображений всех точек предмета образует изображение всего предмета. Рисунок позволяет также легко уяснить причину того, почему изображение предметов всегда получается перевернутым.
Подобным же образом возникает изображение предметов в фотоаппарате при помощи фотографического объектива, который представляет собой собирательную оптическую систему и действует подобно положительной линзе.
Пространство, которое находится перед объективом и в котором расположены фотографируемые предметы, называется предметным пространством, а расположенное за объективом пространство, в котором визуализируются предметы, называется пространством изображений.
Автор: Коллектив авторов. Компиляция: Hyosan. 20 июня 2013 в 09:38
Тэги: Технология фотографии (профессиональная, прикладная)
Источник
Линзой называется прозрачное тело, ограниченное двумя сферическими поверхностями. Если толщина самой линзы мала по сравнению с радиусами кривизны сферических поверхностей, то линзу называют тонкой. Линзы входят в состав практически всех оптических приборов. Линзы бывают собирающими и рассеивающими. Собирающая линза в середине толще, чем у краев, рассеивающая линза, наоборот, в средней части тоньше.
Собирающие (a) и рассеивающие (b) линзы и их условные обозначения.
Прямая, проходящая через центры кривизны O₁ и O₂ сферических поверхностей и оптическим центром линзы O, называется главной оптической осью линзы. Луч света проходя через оптический центр линзы, не отклоняется от первоначального направления. Все прямые, проходящие через оптический центр, называются побочными оптическими осями. Если на линзу направить пучок лучей, параллельных главной оптической оси, то после прохождения через линзу лучи (или их продолжения) соберутся в одной точке F, которая называется главным фокусом линзы. Расстояние между оптическим центром линзы O и главным фокусом F называется фокусным расстоянием.
У тонкой линзы имеются два главных фокуса, симметрично расположенных относительно линзы на главной оптической оси. У собирающих линз фокусы действительные, у рассеивающих – мнимые. Пучки лучей, параллельных одной из побочных оптических осей, также фокусируются после прохождения через линзу в точку F’, которая расположена при пересечении побочной оси с фокальной плоскостью Ф, то есть плоскостью перпендикулярной главной оптической оси и проходящей через главный фокус.
Преломление параллельного пучка лучей в собирающей (a) и рассеивающей (b) линзах. Точки O₁ и O₂ – центры сферических поверхностей, O₁O₂ – главная оптическая ось, O – оптический центр, F – главный фокус, F’ – побочный фокус, OF’ – побочная оптическая ось, Ф – фокальная плоскость.
Основное свойство линз – способность давать изображения предметов. Изображения бывают прямыми и перевернутыми, действительными и мнимыми, увеличенными и уменьшенными. Положение изображения и его характер можно определить с помощью геометрических построений. Для этого используют свойства некоторых стандартных лучей, ход которых известен. Это лучи, проходящие через оптический центр или один из фокусов линзы, а также лучи, параллельные главной или одной из побочных оптических осей.
Построение изображения в собирающей линзе
Если расстояние от предмета до линзы обозначить через d, а расстояние от линзы до изображения через f, то формулу тонкой линзы можно записать в виде:
Величину D, обратную фокусному расстоянию. называют оптической силой линзы. Единица измерения оптической силы является 1 диоптрия (дптр). Диоптрия – оптическая сила линзы с фокусным расстоянием 1 м:
1 дптр = м⁻¹
Линейным увеличением линзы Γ называют отношение линейных размеров изображения h’ и предмета h. Величине h’ удобно приписывать знаки плюс или минус в зависимости от того, является изображение прямым или перевернутым. Величина h всегда считается положительной. Поэтому для прямых изображений Γ > 0, для перевернутых Γ < 0. Из подобия треугольников на рисунке легко получить формулу для линейного увеличения тонкой линзы:
Оптическая сила D линзы зависит как от радиусов кривизны R1 и R2 ее сферических поверхностей, так и от показателя преломления n материала, из которого изготовлена линза. В курсах оптики доказывается следующая формула:
Радиус кривизны выпуклой поверхности считается положительным, вогнутой – отрицательным. Эта формула используется при изготовлении линз с заданной оптической силой.
Спасибо за внимание. Ставьте лайки и подписывайтесь 🙂
Источник
Существуют объекты, которые способны изменять плотность падающего на них потока электромагнитного излучения, то есть либо увеличивать его, собирая в одну точку, либо уменьшать его путем рассеивания. Эти объекты называются линзами в физике. Рассмотрим подробнее этот вопрос.
Что представляют собой линзы в физике?
Под этим понятием подразумевают абсолютно любой объект, который способен изменять направление распространения электромагнитного излучения. Это общее определение линз в физике, под которое попадают оптические стекла, магнитные и гравитационные линзы.
В данной статье главное внимание будет уделено именно оптическим стеклам, которые представляют собой объекты, изготовленные из прозрачного материала, и ограниченные двумя поверхностями. Одна из этих поверхностей обязательно должна иметь кривизну (то есть являться частью сферы конечного радиуса), в противном случае объект не будет обладать свойством изменения направления распространения световых лучей.
Принцип работы линзы

Суть работы этого незамысловатого оптического объекта заключается в явлении преломления солнечных лучей. В начале XVII века знаменитый голландский физик и астроном Виллеброрд Снелл ван Ройен опубликовал закон преломления, который в настоящее время носит его фамилию. Формулировка этого закона следующая: когда солнечный свет переходит через границу раздела двух оптически прозрачных сред, то произведение синуса угла падения между лучом и нормалью к поверхности на коэффициент преломления среды, в которой он распространяется, является величиной постоянной.

Для пояснения вышесказанного приведем пример: пусть свет падает на поверхность воды, при этом угол между нормалью к поверхности и лучом равен θ1. Затем, световой пучок преломляется и начинает свое распространение в воде уже под углом θ2 к нормали к поверхности. Согласно закону Снелла получим: sin(θ1)*n1 = sin(θ2)*n2, здесь n1 и n2 – коэффициенты преломления для воздуха и воды, соответственно. Что такое коэффициент преломления? Это величина, показывающая, во сколько раз скорость распространения электромагнитных волн в вакууме больше таковой для оптически прозрачной среды, то есть n = c/v, где c и v – скорости света в вакууме и в среде, соответственно.
Физика возникновения преломления заключается в выполнении принципа Ферма, согласно которому свет движется таким образом, чтобы за наименьшее время преодолеть расстояние от одной точки к другой в пространстве.
Виды линз

Вид оптической линзы в физике определяется исключительно формой поверхностей, которые ее образуют. От этой формы зависит направление преломления падающего на них луча. Так, если кривизна поверхности будет положительной (выпуклой), то по выходе из линзы световой пучок будет распространяться ближе к ее оптической оси (см. ниже). Наоборот, если кривизна поверхности является отрицательной (вогнутой), тогда пройдя через оптическое стекло, луч станет удаляться от его центральной оси.
Отметим еще раз, что поверхность любой кривизны преломляет лучи одинаково (согласно закону Стелла), но нормали к ним имеют разный наклон относительно оптической оси, в результате получается разное поведение преломленного луча.
Линза, которая ограничена двумя выпуклыми поверхностями, называется собирающей. В свою очередь, если она образована двумя поверхностями с отрицательной кривизной, тогда она называется рассеивающей. Все остальные виды оптических стекол связаны с комбинацией указанных поверхностей, к которым добавляется еще и плоскость. Каким свойством будет обладать комбинированная линза (рассеивающим или собирающим), зависит от суммарной кривизны радиусов ее поверхностей.
Элементы линзы и свойства лучей

Для построения в линзах в физике изображений необходимо познакомиться с элементами этого объекта. Они приведены ниже:
- Главная оптическая ось и центр. В первом случае имеют в виду прямую, проходящую перпендикулярно линзе через ее оптический центр. Последний, в свою очередь, представляет собой точку внутри линзы, проходя через которую, луч не испытывает преломления.
- Фокусное расстояние и фокус – дистанция между центром и точкой на оптической оси, в которую собираются все падающие на линзу параллельно этой оси лучи. Это определение верно для собирающих оптических стекол. В случае рассеивающих линз собираться в точку будут не сами лучи, а мнимое их продолжение. Эта точка называется главным фокусом.
- Оптическая сила. Так называется величина, обратная фокусному расстоянию, то есть D = 1/f. Измеряется она в диоптриях (дптр.), то есть 1 дптр. = 1 м-1.
Ниже приводятся основные свойства лучей, которые проходят через линзу:
- пучок, проходящий через оптический центр, не изменяет направления своего движения;
- лучи, падающие параллельно главной оптической оси, изменяют свое направление так, что проходят через главный фокус;
- лучи, падающие на оптическое стекло под любым углом, но проходящие через его фокус, изменяют свое направление распространения таким образом, что становятся параллельными главной оптической оси.
Приведенные выше свойства лучей для тонких линз в физике (так их называют, потому что не важно, какими сферами они образованы, и какой толщиной обладают, имеют значение только оптические свойства объекта) используются для построения изображений в них.
Изображения в оптических стеклах: как строить?
Ниже приведен рисунок, где подробно разобраны схемы построения изображений в выпуклой и вогнутой линзах объекта (красной стрелки) в зависимости от его положения.
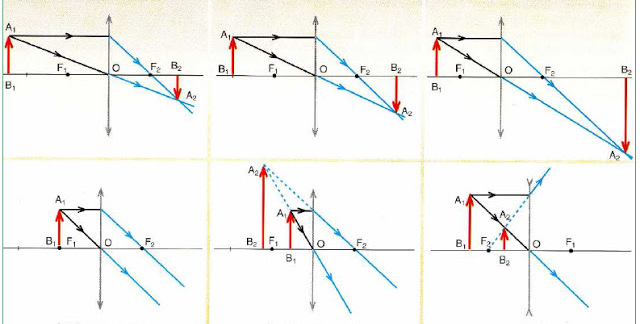
Из анализа схем на рисунке следуют важные выводы:
- Любое изображение строится всего на 2-х лучах (проходящем через центр и параллельном главной оптической оси).
- Собирающие линзы (обозначаются со стрелками на концах, направленными наружу) могут давать как увеличенное, так и уменьшенное изображение, которое в свою очередь может быть реальным (действительным) или мнимым.
- Если предмет расположен в фокусе, то линза не образует его изображения (см. нижнюю схему слева на рисунке).
- Рассеивающие оптические стекла (обозначаются стрелками на их концах, направленными внутрь) дают независимо от положения предмета всегда уменьшенное и мнимое изображение.
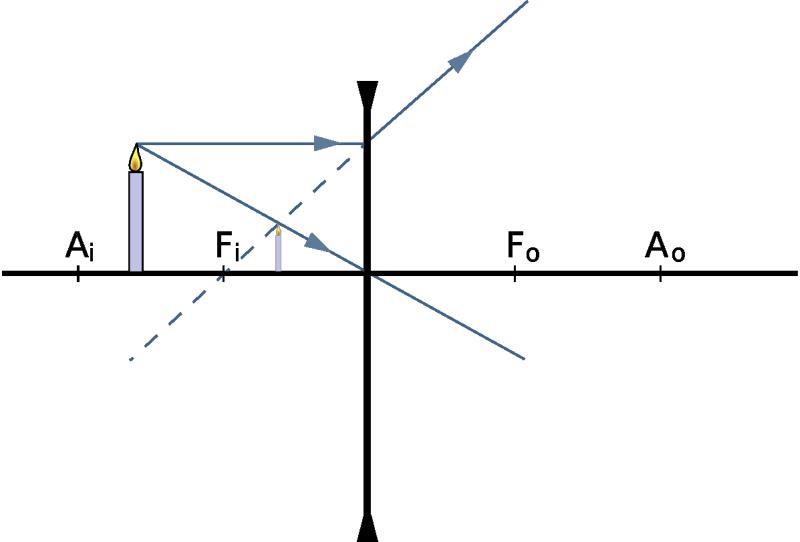
Нахождение расстояния до изображения
Чтобы определять, на каком расстоянии появится изображение, зная положение самого предмета, приведем формулу линзы в физике: 1/f = 1/do + 1/di, где do и di – расстояние до предмета и до его изображения от оптического центра, соответственно, f – главный фокус. Если речь идет о собирающем оптическом стекле, тогда число f будет положительным. Наоборот, для рассеивающей линзы f – отрицательное.
Воспользуемся этой формулой и решим простую задачу: пусть предмет находится на расстоянии do = 2*f от центра собирающего оптического стекла. Где появится его изображение?
Из условия задачи имеем: 1/f = 1/(2*f)+1/di. Откуда: 1/di = 1/f – 1/(2*f) = 1/(2*f), то есть di = 2*f. Таким образом, изображение появится на расстоянии двух фокусов от линзы, но уже с другой стороны, чем сам предмет (об этом говорит положительный знак величины di).
Краткая история
Любопытно привести этимологию слова “линза”. Оно ведет происхождение от латинских слов lens и lentis, что означает “чечевица”, поскольку оптические объекты по своей форме действительно похожи на плод этого растения.
Преломляющая способность сферических прозрачных тел была известна еще древним римлянам. Для этой цели они применяли круглые стеклянные сосуды, наполненные водой. Сами же стеклянные линзы начали изготавливаться только в XIII веке в Европе. Использовались они в качестве инструмента для чтения (современные очки или лупа).
Активное использование оптических объектов при изготовлении телескопов и микроскопов относится к XVII (в начале этого века Галилей изобрел первый телескоп). Отметим, что математическая формулировка закона преломления Стелла, без знания которой невозможно изготавливать линзы с заданными свойствами, была опубликована голландским ученым в начале того же XVII века.
Другие виды линз
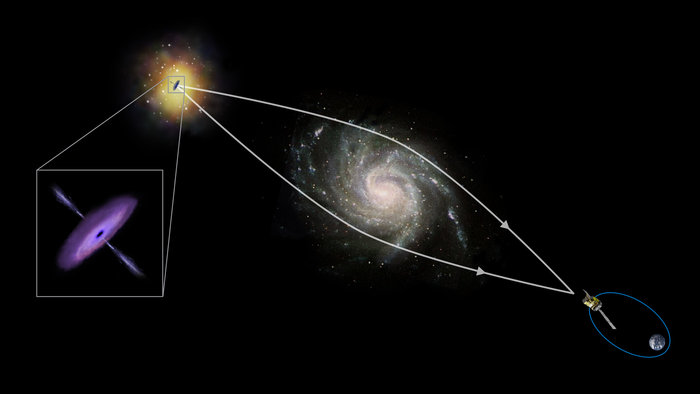
Как было отмечено выше, помимо оптических преломляющих объектов, существуют также магнитные и гравитационные. Примером первых являются магнитные линзы в электронном микроскопе, яркий пример вторых заключается в искажении направления светового потока, когда он проходит вблизи массивных космических тел (звезд, планет).
Источник
Линза. Формула тонкой линзы.
Классификация линз по внешней форме и оптическим
свойствам.
“Линза – слово
латинское и означает чечевица. Чечевица – растение, плоды которого похожи на
горох, но горошины не круглые, а имеют вид пузатых лепешек. Поэтому все круглые
стекла, имеющие такую форму, стали называть – линзами.”
Линзы по внешней форме выделяют 6 видов.
Линза может быть:
– ограничена двумя выпуклыми сферическими поверхностями –
двояковыпуклая линза — рис. 1а,
– выпуклой сферической поверхностью и плоскостью –
плосковыпуклая линза — рис. 1б,
– выпуклой и вогнутой сферическими поверхностями –
вогнуто-выпуклая линза — рис. 1 в.
Эти линзы посредине толще, чем у краев, и все они называются выпуклыми.

Линзы, которые посредине тоньше, чем у краев, называются вогнутыми.
На рисунке 2 изображены три вида вогнутых линз:
– двояковогнутая –
а, – плосковогнутая –
б, – выпукло-вогнутая –
в.
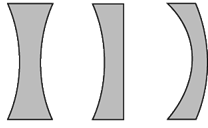
По оптическим свойствам линзы делятся на:
собирающие (выпуклые) и рассеивающие (вогнутые).
К группе собирательных линз обычно относят линзы, у которых
середина толще их краёв, а к группе рассеивающих — линзы, края которых толще
середины. Следует отметить, что это верно, только если показатель преломления у
материала линзы больше, чем у окружающей среды. Если показатель преломления
линзы меньше, ситуация будет обратной. Например пузырёк воздуха в воде —
двояковыпуклая рассеивающая линза.
Обычно линзы изготавливаются из стекла. Выпуклые линзы являются
собирающими. Вогнутые линзы, находящиеся в оптически менее плотной среде (по
сравнению с материалом линзы), являются рассеивающими.
Собирающие и
рассеивающие линзы
Отличительным
свойством собирательной линзы является способность собирать падающие на её
поверхность лучи в одной точке, расположенной по другую сторону линзы.
Собирающая линза 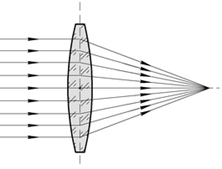

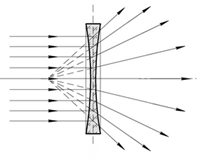
Рассеивающая линза

Сферические поверхности линзы могут иметь различную кривизну (степень
выпуклости/вогнутости).
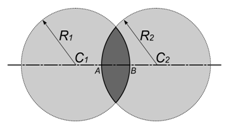
Рис 3. С1 и С2 – центры ограничивающих
линзу сферических поверхностей, они называются центрами
кривизны. R1 и R2 – радиусы сферических
поверхностей линзы или радиусы
кривизны.
Тонкие линзы
Линзы, толщина которых пренебрежимо мала по сравнению с радиусами
сферических поверхностей (кривизны), называют тонкими.
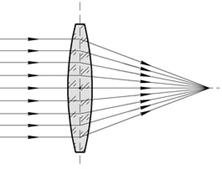
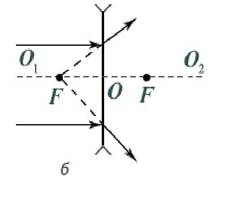
Тонкие собирающие линзы: Тонкие рассевающие


Характеристики линз.
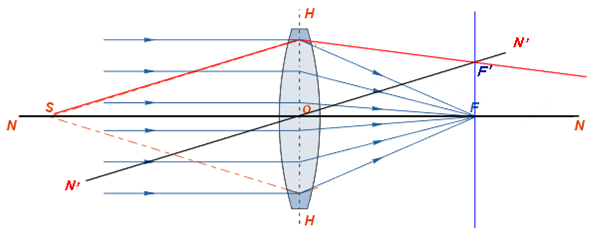
Главная оптическая ось – NN –
прямая линия, проходящая через центры сферических поверхностей, ограничивающих
линзу;
Оптический центр O –
это точка, лежащая на оптической оси, через которую любой луч проходит не
изменяя своего направления..
Побочная ось линзы N’N’ –
любая прямая, проходящая через оптический центр, но не совпадающая с главной
оптической осью
Главный фокус линзы F –
точка, в которой пересекаются после преломления в собирающей линзе лучи. У линзы
два главных фокуса. В однородной среде они располагаются по обе стороны линзы на
одинаковых расстояниях от нее.
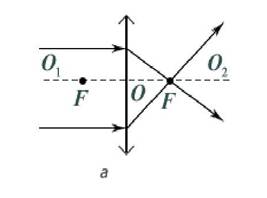
Фокусное расстояние OF –
расстояние от оптического центра линзы до ее фокусов. У вогнутых линз фокусное
расстояние выражается отрицательным числом.
Фокальная плоскость – плоскость,
проходящая через главный фокус перпендикулярно главной оптической оси.
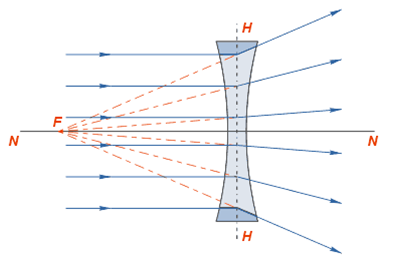
Лучи, падающие на
рассеивающую линзу, по выходе из неё будут преломляться в сторону краёв линзы,
то есть рассеиваться. Если эти лучи продолжить в обратном направлении так, как
показано на рисунке пунктирной линией, то они сойдутся в одной точке F, которая
и будет фокусом этой линзы. Этот фокус будет мнимым.
Характеристики изображения.
1) Изображение может быть мнимое или действительное.
Если изображение образовано самими лучами (т.е. в данную точку поступает
световая энергия), то оно действительное, если же не самими лучами, а их
продолжениями, то говорят, что изображение мнимое (световая энергия не поступает
в данную точку).
2) Если верх и низ изображения ориентированы аналогично самому
предмету, то изображение называется прямым.
Если же изображение перевернуто, то его называют обратным
(перевернутым).
3) Изображение характеризуется приобретаемыми размерами:
увеличенное, уменьшенное, равное.
Построение изображения в линзах.
Линза, для которой толщина принята равной нулю, в оптике
называется «тонкой». Для такой линзы показывают не две главных
плоскости, а одну, в которой как бы сливаются вместе передняя и задняя.
Положение изображения и его характер можно определить с помощью
геометрических построений.
Рассмотрим построение хода луча произвольного направления в
тонкой собирающей линзе. Для этого используют свойства некоторых стандартных
лучей, ход которых известен. Это:
1) луч, проходящий через оптический центр линзы (О), не
испытывает преломления;
2) луч, падающий на линзу параллельно главной оптической оси,
после преломления проходит через главный фокус (F);
3) луч, проходящий через фокус (F), после преломления идет
параллельно главной оптической оси.
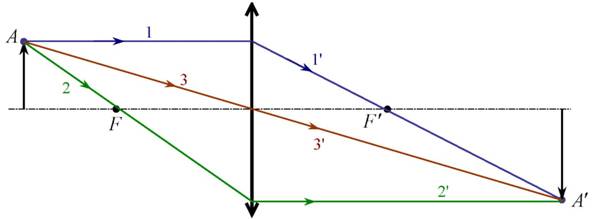
Построение изображения в собирающей
линзе
1. Предмет находится
между фокусом и двойным фокусом линзы
Характеристика
изображения: увеличенное, перевернутое, действительное
2. Предмет находится
за двойным фокусом линза
Характеристика
изображения: уменьшенное, перевернутое, мнимое
3. Предмет находится
между линзой и фокусом линзы
Характеристика
изображения: увеличенное, прямое, мнимое
4. Предмет находится в фокусе линзы
Характеристика
изображения: Изображение отсутвует
5. Предмет находится в
двойном фокусе линзы
Характеристика
изображения: изображение равно по размерам предмету, перевернутое,
действительное
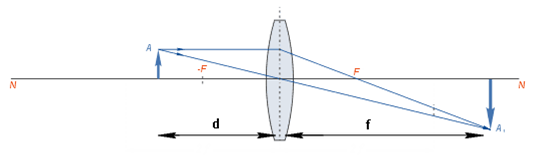
Построение изображения в рассеивающей линзе
Характеристика
изображения: уменьшенное, прямое, мнимое
Формула линзы.
1. Формула тонкой линзы
Формула тонкой линзы, связывающая расстояние d
от предмета до линзы, расстояние f от изображения до
линзы и F фокусное расстояние линзы.
(1)
d
– расстояние от предмета до линзы,
(м).
f
–
расстояние от линзы до изображения,
(м).
F
– фокусное расстояние линзы, это расстояние от оптического центра линзы до ее
фокусов, (м)
.
При использовании формулы линзы
следует верно использовать правило знаков:
F > 0 – линза
собирающая; F < 0 – линза
рассеивающая.
f > 0 – изображение действительное, f < 0 – изображение
мнимое
Оптическая сила линзы
D
–
это величина обратная фокусному расстоянию.
, (2)
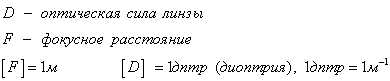
За единицу оптической силы принята –
диоптрия (1 дптр ).
1 диоптрия – это оптическая сила такой линзы, фокусное расстояние
которой равно 1 метр.
2. Фокусное расстояние собирающей линзы по линейному увеличению
Линейное увеличение –
Г – отношение линейного размера изображения к линейному размеру предмета.
Из подобии треугольников АОВ и А1ОВ1 ( см. рисунок),
следует, что
(3)
Г – увеличение линзы, [ Г ]
– безразмерная величина
Н – линейные размеры изображения. [ H ]
– 1 м
h – линейные размеры
предмета. [ h ]
– 1 м
f – расстояние от
изображения предмета до линзы [ f ]
– 1 м
d – расстояние от
предмета до линзы [ d ]
– 1 м
Учитывая формулу (1) и (3) получим выражения для определения
фокусного расстояния собирающей линзы по линейному увеличению.
(4)
3.
Фокусное расстояние собирающей линзы по радиусам
кривизны сферических поверхностей
Задачи:
1. Главное фокусное
расстояние рассеивающей линзы 12 см. Изображение предмета находится на
расстоянии 9 см от линзы. Чему равно расстояние от предмета до линзы?
2. Предмет расположен
на расстоянии 1,6F от линзы. Его приблизили к линзе на
0,8F.
На сколько при этом переместилось изображение предмета, если оптическая сила
линзы 2,5 дптр?
3. Мнимое изображение
предмета, получаемое с помощью линзы в 4,5 раза больше самого предмета. Чему
равна оптическая сила линзы, если предмет находится на расстоянии 3,8 см от
линзы?
4. Предмет высотой 6
см расположен на главной оптической оси тонкой собирающей линзы на расстоянии 30
см от ее оптического центра. Оптическая сила линзы 5 дптр. Найдите высоту
изображения предмета. Ответ выразите в сантиметрах (см)
Контрольные вопросы:
1. Какую линзу
называют тонкой
2. Что называется
главным фокусом линзы?
3. Какие лучи удобно
использовать для построения изображения в линзе?
4. Что называется
увеличением линзы?
5. Перечислите виды
линз
6. Запишите формулы,
определяющие фокус линзы
Домашнее задание:
Задачи:
1. Предмет находиться
на расстоянии 4F. Во сколько раз его изображение на экране меньше изображения
предмета?
2. Расстояние от
предмета до экрана 90см. Где надо поместить между ними линзу с фокусным
расстоянием 20см, чтобы получить четкое изображение?
3. Пучок параллельных
световых лучей падает перпендикулярно на тонкую собирающую линзу оптической
силой 5 дптр. Диаметр линзы 6 см. Диаметр светлого пятна на экране 12 см. На
каком расстоянии (в см) от линзы помещен экран
Источник
