Какими свойствами обладают катушки индуктивности
Катушка индуктивности в электрической цепи хорошо проводит постоянный ток и в то же время оказывает сопротивление переменному току, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению.
Катушка индуктивности обладает реактивным сопротивлением величина которого равна: 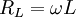 , где
, где 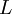 — индуктивность катушки,
— индуктивность катушки, 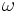 — угловая частота протекающего тока. Соответственно, чем больше частота тока, протекающего через катушку, тем больше её сопротивление.
— угловая частота протекающего тока. Соответственно, чем больше частота тока, протекающего через катушку, тем больше её сопротивление.
При протекании тока катушка запасает энергию, равную работе, которую необходимо совершить для установления текущего тока 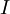 . Величина этой энергии равна
. Величина этой энергии равна 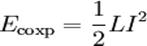
При изменении тока в катушке возникает ЭДС самоиндукции, значение которой 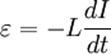
Характеристики катушки индуктивности
Индуктивность
Основным параметром катушки индуктивности является её индуктивность, которая определяет, какой поток магнитного поля создаст катушка при протекании через неё тока силой 1 ампер. Типичные значения индуктивностей катушек от десятых долей мкГн до десятков Гн.
Значение индуктивности катушки индуктивности пропорционально линейным размерам катушки, квадрату числа витков намотки и магнитной проницаемости сердечника и изменяется от десятых долей мкгн до десятков гн. К основным параметрам катушки индуктивности относятся сопротивление потерь, добротность, температурный коэффициент индуктивности, собственная ёмкость. Катушки индуктивности широко применяют в качестве элементов фильтров и колебательных контуров, в трансформаторах, в качестве дросселей, в реле, магнитных усилителях, электромагнитах и др.
Разновидностью Катушки индуктивности являются плоские печатные катушки индуктивности, применяемые в микромодулях, а также обмотки электрических машин, рамочные и ферритовые антенны.
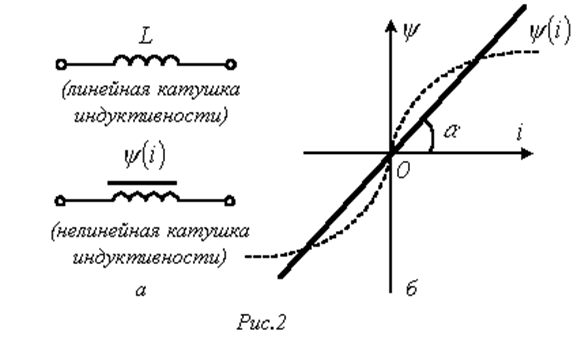
Условное графическое изображение катушки индуктивности приведено на рис. 2,а. Катушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета индуктивности катушки необходимо рассчитать созданное ею магнитное поле.
Индуктивность определяется отношением потокосцепления к току, протекающему по виткам катушки,
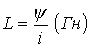 .
.
В свою очередь потокосцепление равно сумме произведений потока, пронизывающего витки, на число этих витков 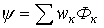 , где
, где 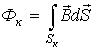 .
.
Основной характеристикой катушки индуктивности является зависимость 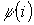 , называемая вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость
, называемая вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость 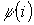 представляет собой прямую линию, проходящую через начало координат (см. рис. 2,б); при этом
представляет собой прямую линию, проходящую через начало координат (см. рис. 2,б); при этом
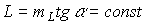 .
.
Нелинейные свойства катушки индуктивности (см. кривую 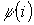 на рис. 2,б) определяет наличие у нее сердечника из ферромагнитного материала, для которого зависимость
на рис. 2,б) определяет наличие у нее сердечника из ферромагнитного материала, для которого зависимость 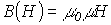 магнитной индукции от напряженности поля нелинейна. Без учета явления магнитного гистерезиса нелинейная катушка характеризуется статической
магнитной индукции от напряженности поля нелинейна. Без учета явления магнитного гистерезиса нелинейная катушка характеризуется статической 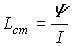 и дифференциальной
и дифференциальной 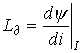 индуктивностями.
индуктивностями.
Индуктивность катушки пропорциональна линейным размерам катушки, квадрату числа витков намотки и магнитной проницаемости сердечника. При последовательном соединении катушек общая индуктивность равна сумме индуктивностей всех соединённых катушек. 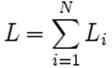
Индуктивность является основным параметром катушки индуктивности. Ее величина (мкТн) определяется соотношением
где W – число витков, D – диаметр катушки в см, L0 – коэффициент, зависящий от отношения длины катушки / к ее диаметру О.
Для однослойных катушек величина L0 определяется соотношением
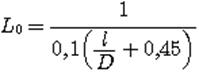 |
Оптимальными в этом случае являются отношение 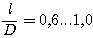 а диаметр катушки в пределах от 1 до 2 см. При расчете диаметр катушки D принимается равным диаметру каркаса D
а диаметр катушки в пределах от 1 до 2 см. При расчете диаметр катушки D принимается равным диаметру каркаса D
Для многослойных катушек величина L0зависит не только от величины 1/D , но и от отношения толщины намотки t к диаметру катушки D. Она определяется по графикам (рис.2.24). В этом случае внешний диаметр катушки D=D0 + 2t
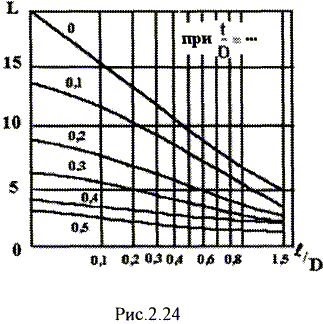
При расчете катушки индуктивности предварительно задаются геометрическими размерами катушки и определяют коэффициент L0, а затем по заданной величине индуктивности L находят число витков:
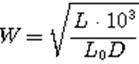 |
где I, – в мкГн , D – в см.
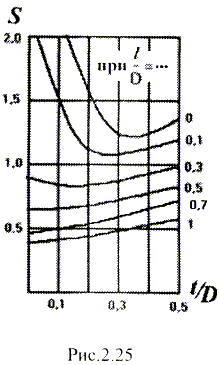
Для намотки катушки обычно применяют провод оптимального диаметра, который рассчитывается с помощью эмпирических формул и графиков. Для этого по графику S=f(t/D;l/D) (рис.2.25) находят вспомогательный коэффициент S. Затем рассчитывают коэффициент
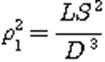 |
где f -в мкГц , D – в см. Затем рассчитывают коэффициентa1
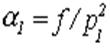
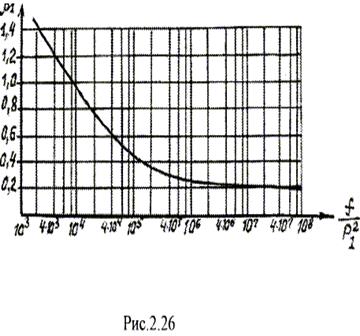
где f – частота в Гц. После чего по графику b1=f(a1) (рис. 2.26) находят вспомогательный коэффициент b1S и расчитывают оптимальный диаметр провода (мм)
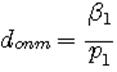 |
Полученное значение округляется до ближайшего стандартного значения (табл.2.6) и выбирается марка провода с диаметром dиз
Основные параметры обмоточных проводов
Таблица 2.6
| d, мм | Sn, мм~ | Максимальный диаметр в изоляции , мм | |||
| ПЭВТЛК | ПЭМ-1 | ПЭВ-1 | ПЭВ-2,ПЭТВ ПЭМ-2 | ||
| 0,063 | 0,0028 | 0.11 | 0,09 | 0,085 | 0,09 |
| 0,071 | 0,0038 | 0,12 | 0,09 | 0,095 | 0,1 |
| 0,08 | 0,005 | 0,13 | 0,1 | 0,105 | 0,11 |
| 0,09 | 0,0064 | 0,14 | 0,11 | 0,115 | 0,12 |
| 0,1 | 0,0079 | 0,15 | 0,12 | 0,125 | 0,13 |
| 0,112 | 0,0095 | 0,16 | 0,14 | 0,135 | 0,14 |
| 0,125 | 0,0113 | 0,17 | 0,15 | 0,15 | 0,155 |
| 0,14 | 0,0154 | 0,185 | 0,16 | 0,165 | 0,17 |
| 0,16 | 0,02 | 0,2 | 0,19 | 0,19 | 0,2 |
| 0,18 | 0,0254 | 0,23 | 0,21 | 0,21 | 0,22 |
| 0,2 | 0,0314 | 0,25 | 0,23 | 0,23 | 0,24 |
| 0,224 | 0,0415 | 0,27 | 0,25 | 0,26 | 0,27 |
| 0,25 | 0,0491 | 0,3 | 0,29 | 0,29 | 0,3 |
| 0,28 | 0,0615 | 0,34 | 0,32 | 0,32 | 0,33 |
| 0,315 | 0,0755 | 0,37 | 0,35 | 0,355 | 0,365 |
| 0,355 | 0,0962 | 0,405 | 0,39 | 0,395 | 0,415 |
| 0,4 | 0,126 | 0,47 | 0,44 | 0,44 | 0,46 |
| 0,45 | 0,158 | – | 0,49 | 0,49 | 0,51 |
| 0,5 | 0,193 | – | 0,55 | 0,55 | 0,57 |
| 0,56 | 0,246 | – | 0,61 | 0,61 | 0,63 |
| 0,63 | 0,311 | – | 0,68 | 0,68 | 0,7 |
| 0,71 | 0,39 | – | 0,76 | 0,76 | 0,79 |
| 0,75 | 0.435 | – | 0,81 | 0,81 | 0,84 |
| 0,8 | 0,503 | – | 0,86 | 0,86 | 0,89 |
| 0,85 | 0,567 | – | 0,91 | 0,91 | 0,94 |
| 0,9 | 0,636 | – | 0,96 | 0,96 | 0,99 |
| 0,95 | 0,71 | – | 1,01 | 1,01 | 1,04 |
| 0,785 | – | 1,08 | 1,07 | 1, 11 |
После выбора оптимального диаметра провода проверяют возможность размещения обмотки в заданных размерах l и t. Для однослойных катушек рассчитывают шаг намотки
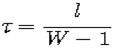 |
Если t>dиз то обмотка размещается. В противном случае задаются большей величиной l и повторяют расчет.
Для многослойных катушек рассчитывают толщину обмотки
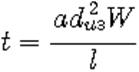 |
где а – коэффициент неплотности обмотки ( a = 1,05…1,3), и находят фактическое значение наружного диаметра катушки D=D0+2t. Если эта величина отличается от выбранной в начале расчета более чем на 10%, то задаю тся новыми значениями l и t и расчет повторяют. При помещении катушки в экран индуктивность катушки уменьшается
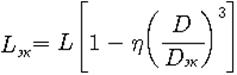 |
где h – коэффициент, зависящий от отношения l/D (рис.2.27),
D – диаметр катушки, Dэк-диаметр экрана.
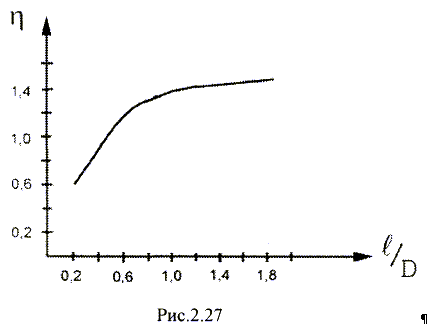
Индуктивность уменьшается тем больше, чем меньше диаметр экрана. В большинстве случаев Dэк/D >1,6¸1,8.При этом индуктивность уменьшается не более чем на 20%.
Многослойные катушки обычно выполняют с сердечниками броневого типа, при использовании которых большая часть силовых линий магнитного поля катушки замыкается через сердечник, а меньшая-через воздух, вследствие чего влияние экрана на индуктивность катушки значительно ослабляется.
Применение сердечников из магнитных материалов позволяет уменьшить число витков катушки индуктивности и соответственно ее габариты. Основным параметром сердечника является магнитная проницаемость mс При его наличии индуктивность катушки становится равной
Поскольку в расчетные формулы входят эмпирические коэффициенты, то индуктивность изготовленной катушки отличается от расчетной. Применение подстроечных магнитных сердечников позволяет получить требуемое значение индуктивности.
Собственная емкость является паразитным параметром катушки индуктивности, ограничивающим возможности ее применения. Ее возникновение обусловлено конструкцией катушки индуктивности: емкость существует между отдельными витками катушки, между витками и сердечником, витками и экраном, витками и другими элементами конструкции. Все эти распределенные емкости можно объединить в одну, называемую собственной емкостью катушки CL.
Наименьшей собственной емкостью обладают однослойные катушки индуктивности Приближенно она рассчитывается по формуле (пФ)
где D – диаметр катушки в см. Обычно она не превышает 1-2пФ.
Собственная емкость многослойных катушек значительно больше. При многослойной рядовой намотке она достигает ЗОпФ; при намотке “внавал” она несколько меньше. Существенное уменьшение емкости многослойных катушек достигается при использовании универсальной обмотки, при выполнении которой провод укладывается под некоторым углом к образующей цилиндрического каркаса. Схема такой намотки показана на рис.2.28. Как только провод доходит до края катушки, направление укладки меняется. Цикл универсальной обмотки выбирается таким, что, совершив один оборот вокруг каркаса, провод возвращается к положение, отличающееся от исходного на угол b. Этот угол выбирается таким, чтобы каждый последующий виток находился рядом с предыдущим.
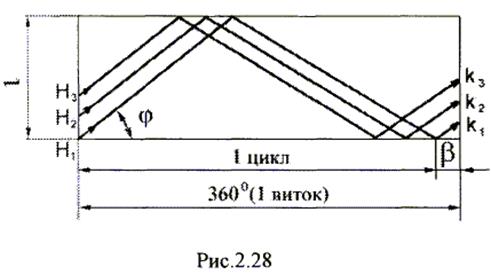
Очевидно, что
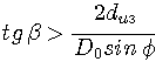 |
Угол j , под которым осуществляется укладка провода, находится из соотношения
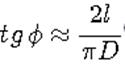 |
где l-осевая длина катушки,D – диаметр витка.
Наименьшее значение угла j получается для витков, имеющих наименьший диаметр, равный диаметру каркаса D0.
Обычно при использовании универсальной обмотки длину катушки принимают в пределах от 2 до 10мм. Количество циклов намотки связано с рачетнным числом витков W соотношением
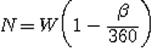 |
Величина собственной емкости катушек с универсальной обмоткой составляет от 3 до 8пФ. Дополнительное снижение емкости достигается серкцонированием обмотки.
Совместное действие индуктивности и емкости можно учесть введением понятия об эквивалентной индуктивности катушки, определяемой из уравнения
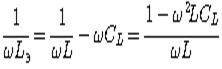
откуда
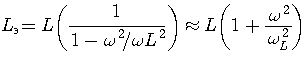 |
где 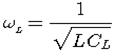 -собственная резонансная частота катушки индуктивности.
-собственная резонансная частота катушки индуктивности.
Если рабочая частота много ниже собственной резонансной частоты wL, то приближенно можно считать Lэ=L.
В процессе работы на катушку действуют различные внешние факторы: температура, влага и другие, влияющие на ее индуктивность. Наиболее существенным является влияние температуры, которое оценивают температурным коэффициентом 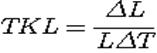 .
.
Температурная нестабильность индуктивности обусловлена целым рядом факторов: при нагреве увеличивается длина и диаметр провода обмотки, увеличивается длина и диаметр каркаса, в результате чего изменяются шаг и диаметр витков; кроме того при изменении температуры изменяются диэлектрическая проницаемость материала каркаса, что ведет к
изменению собственной емкости катушки.
Для повышения температурной стабильности применяют каркасы из материала с малым значением коэффициента линейного расширения. Этим требованиям в наибольшей степени удовлетворяет керамика. Повышению температурной стабильности катушек способствует прочное сцепление обмотки с каркасом. С этой целью обмотку выполняют методом вжигания серебра в керамический каркас. В этом случае изменение размеров токопроводящего слоя определяется только линейным расширением каркаса. Такие катушки индуктивности имеют TKL >(5-100).10-6 Стабильность многослойных катушек существенно хуже, так как в них невозможно избежать изменения линейных размеров провода обмотки. Многослойные катушки имеют TKL>(50-100).10-6
Источник
Приветствую всех на нашем сайте!
Мы продолжаем изучать электронику с самых основ, и темой сегодняшней статьи будет катушка индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы.
Устройство и принцип работы катушки индуктивности.
Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку ???? То есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:

Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название ???? Индуктивность – это способность преобразовывать энергию электрического поля в энергию магнитного поля. Это свойство катушки связано с тем, что при протекании по проводнику тока вокруг него возникает магнитное поле:
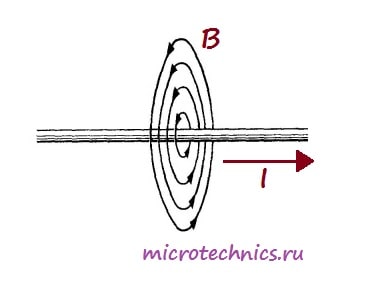
А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:
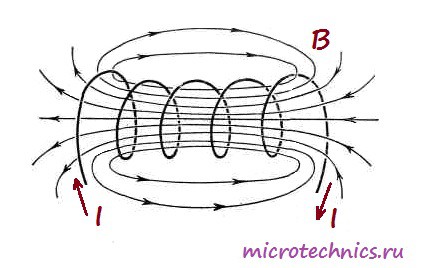
В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри – это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину индуктивности катушки можно рассчитать по следующей формуле:
L = frac{mu_0thinspace mu S N^2}{l}
Давайте разберемся, что за величину входят в это выражение:
- mu_0 – магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению: mu_0 = 4 pi cdot 10^{-7}medspacefrac{Гн}{м}
- mu – магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз
- S – площадь поперечного сечения катушки
- N – количество витков
- l – длина катушки
Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.
С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный!
Катушка индуктивности в цепи постоянного тока.
Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет ???? Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:

Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель?
Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:
varepsilon_s = -frac{dPhi}{dt}
Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
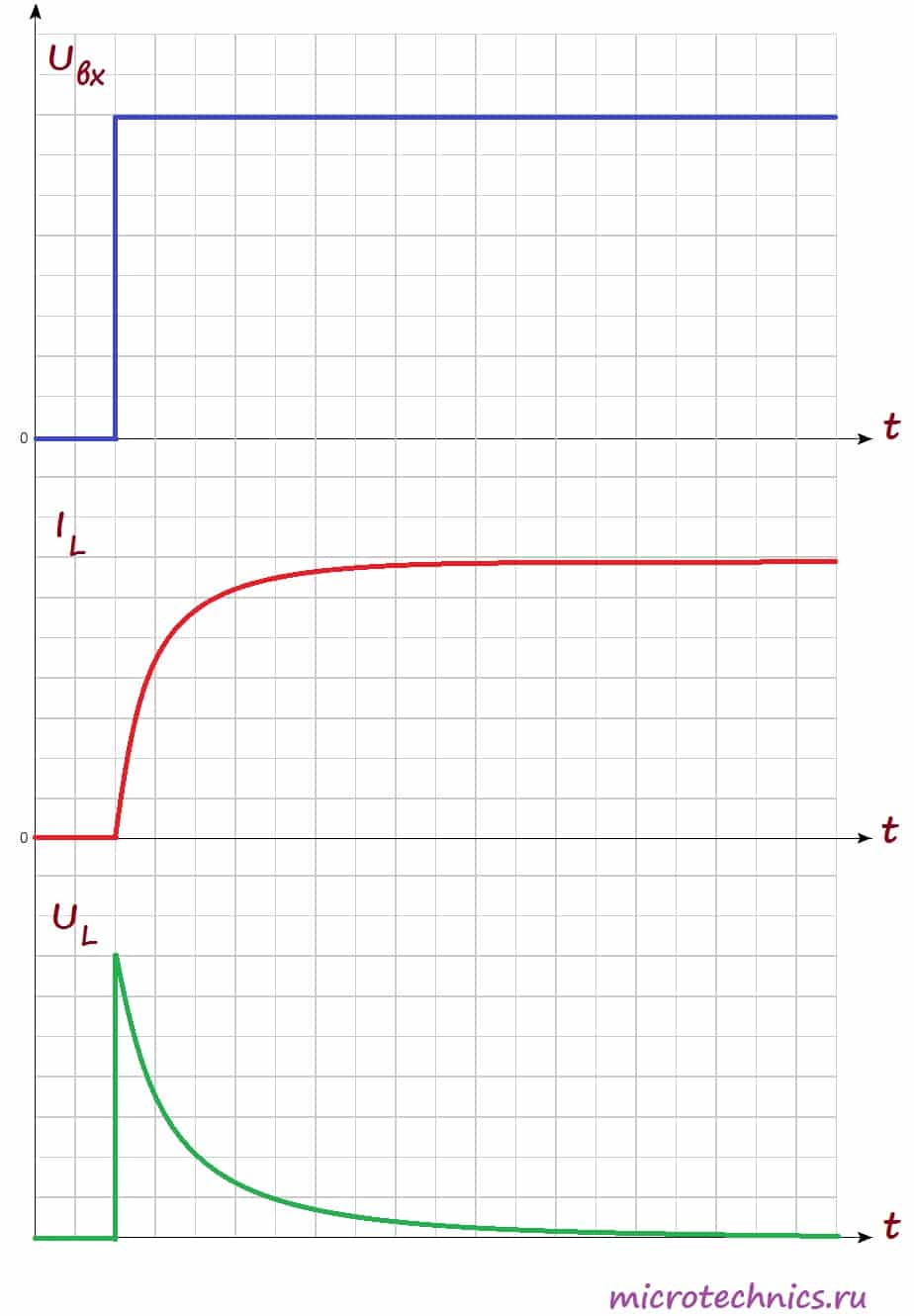
На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать.
Напряжение на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
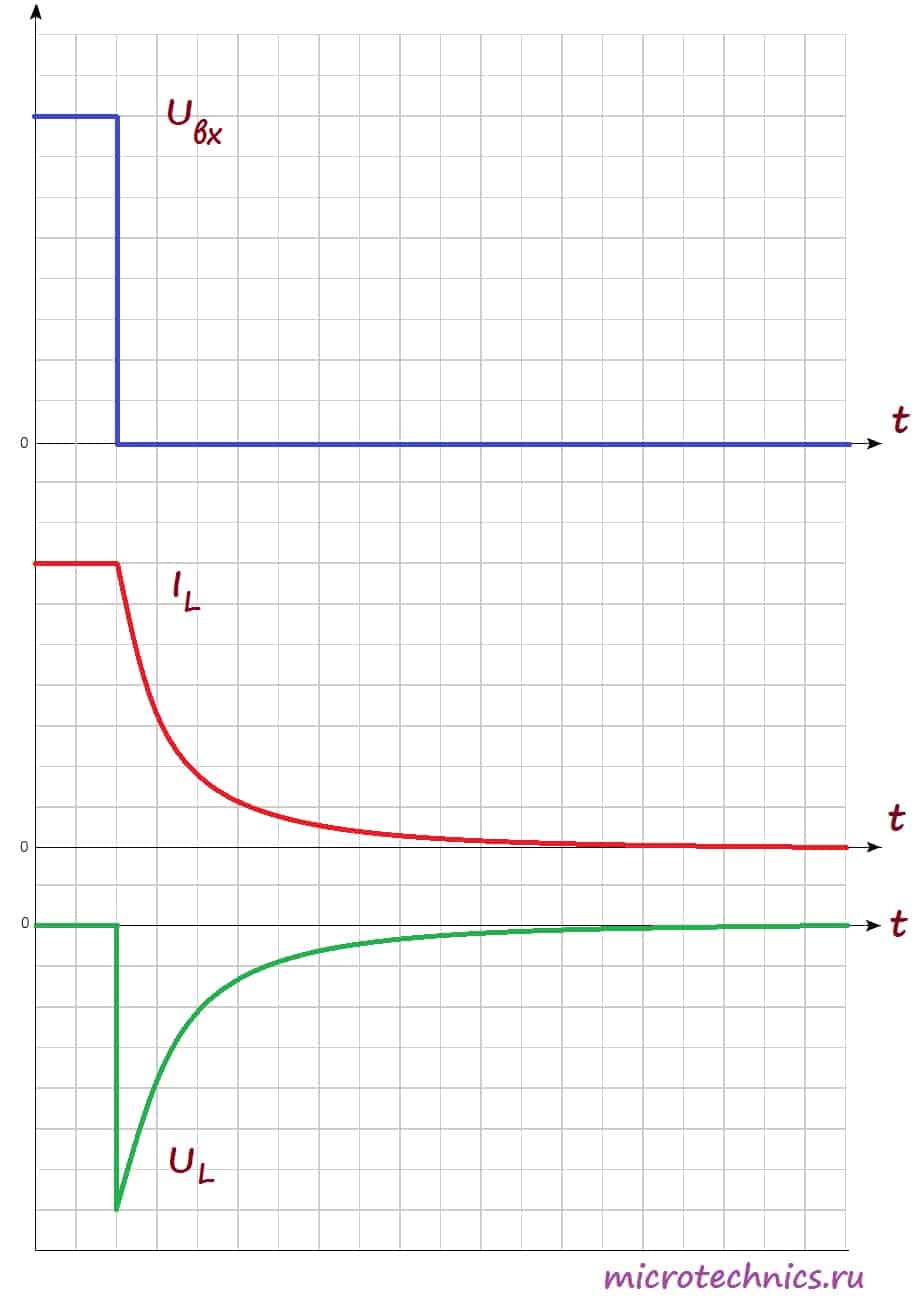
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:
varepsilon_s = -Lmedspacefrac{dI}{dt}
На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.
Катушка индуктивности в цепи переменного тока.
Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:
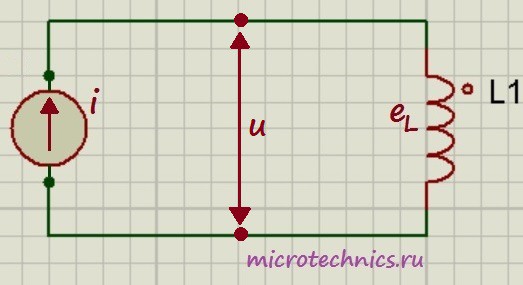
Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:
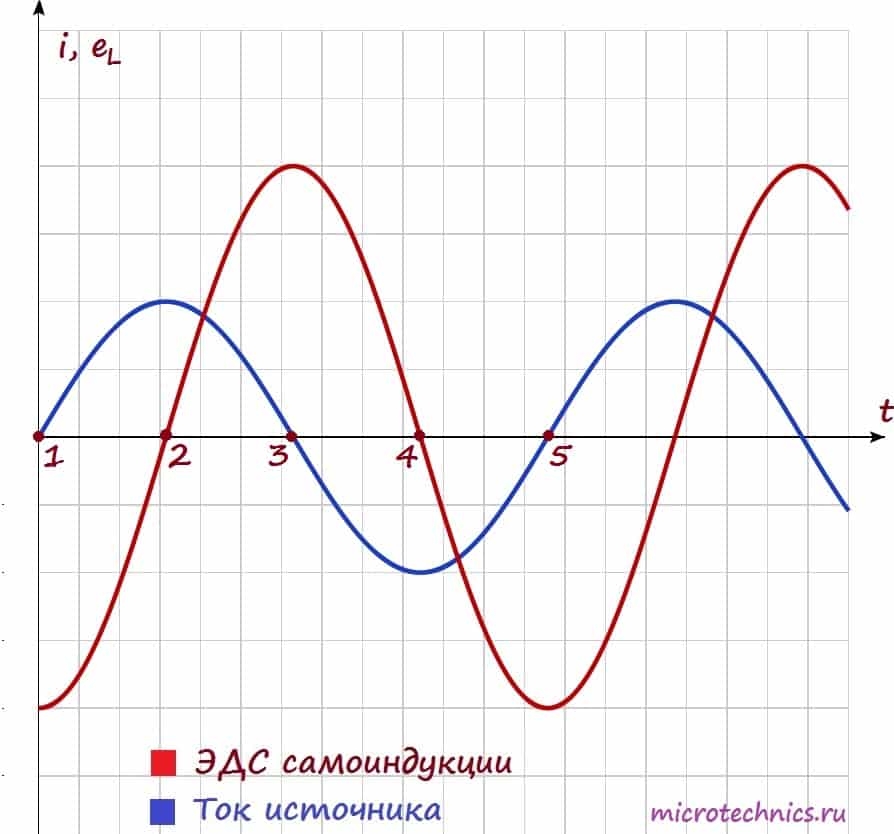
Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:
varepsilon_L = -Lmedspacefrac{dI}{dt}
Собственно, график нам и демонстрирует эту зависимость! Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.
Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу ????
Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: varepsilon < 0, i > 0, участок 3-4: varepsilon > 0, i < 0). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника).
А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока).
И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:
X_L = wmedspace L
Где w – круговая частота: w = 2 pi f. [/latex]f[/latex] – это частота переменного тока. Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный (f = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.
Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение u? Здесь все на самом деле просто! По 2-му закону Кирхгофа:
u + varepsilon_L = 0
А следовательно:
u = – varepsilon_L
Построим на одном графике зависимости тока и напряжения в цепи от времени:
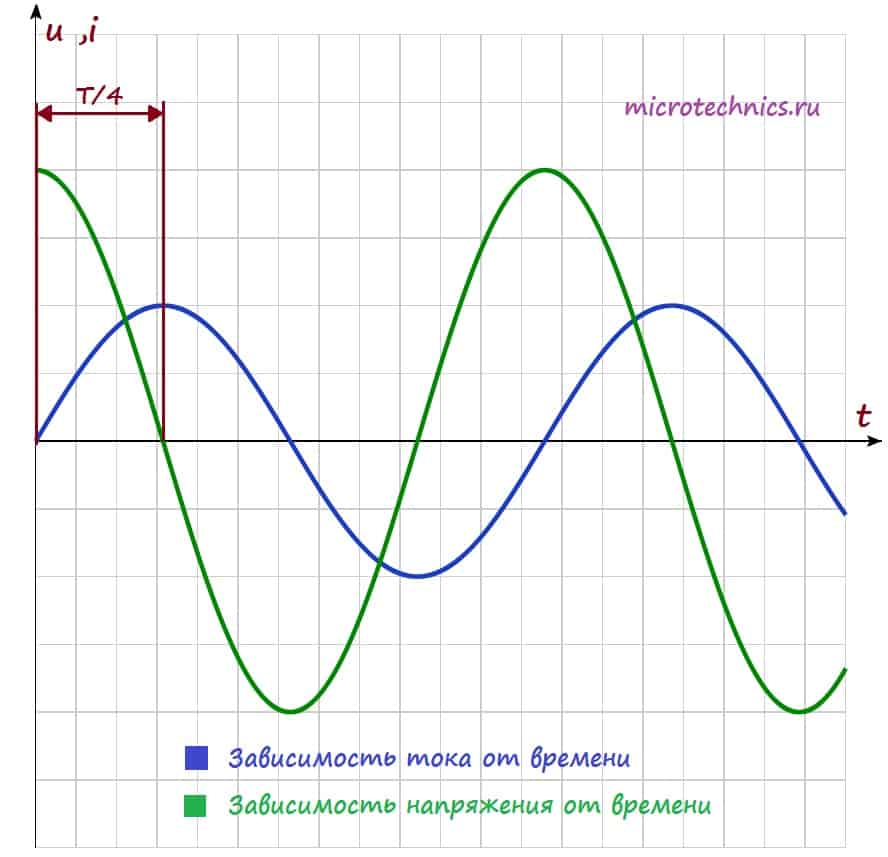
Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:
При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода.
Вот и с включением катушки в цепь переменного тока мы разобрались!
На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому разговор о катушках индуктивности мы продолжим в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!
Источник
