Какими свойствами обладает точечный заряд
Электрический заряд и его основные свойства.
Закон сохранения электрического заряда.
Электрический заряд – это скалярная физическая величина, определяющая интенсивность электромагнитных взаимодействий. Единица заряда – [q] кулон.
Свойства электрического заряда:
1. Электрический заряд не является знакоопределенной величиной, существуют как положительные, так и отрицательные заряды.
2. Электричесий заряд – величина инвариантная. Он не изменяется при движении носителя заряда.
3. Электричесий заряд аддитивен.
4. Электричесий заряд кратен элементарному. q = Ne. Это свойство заряда называется дискретностью (квантованностью).
5. Суммарныйэлектричесий заряд всякой изолированной системы сохраняется. Это свойство естьзакон сохранения электрического заряда.
Закон сохранения электрического заряда – электрические заряды не создаются и не исчезают, а только передаются от одного тела к другому или перераспределяются внутри тела.
Электростатика. Точечный заряд. Закон Кулона. Принцип суперпозиции сил. Объемная поверхностная и линейная плотность заряда.
Электростатика — раздел учения об электричестве, изучающий взаимодействие неподвижных электрических зарядов.
Точечный заряд – это заряженное тело, размерами и формой, которого можно пренебречь.
Формулировка закона Кулона: Сила электростатического взаимодействия между двумя точечными электрическими зарядами прямо пропорциональна произведению величин зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей их прямой так, что одноименные заряды отталкиваются, а разноименные притягиваются.
Принцип суперпозиции сил заключается в том, что действие нескольких сил можно заменить действием одной – равнодействующей. Равнодействующей называется единственная сила, результат действия которой эквивалентен одновременному действию всех сил, приложенных к этому телу.
Линейная плотность заряда: заряд, приходящийся на единицу длины.
Поверхностная плотность заряда: заряд, приходящийся на единицу площади.
Объемная плотность заряда: заряд, приходящийся на единицу объема.
Напряженность электрического поля. Силовые линии электростатического поля. Напряженность поля неподвижного точечного заряда. Электростатическое поле. Принцип суперпозиции.
Напряжённость электрического поля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на неподвижный точечный заряд, помещённый в данную точку поля, к величине этого заряда q.
Силовые линии электростатического поля имеют следующие свойства:
1. Всегда незамкнуты: начинаются на положительных зарядах (или на бесконечности) и заканчиваются на отрицательных зарядах (или на бесконечности).
2. Не пересекаются и не касаются друг друга.
3. Густота линий тем больше, чем больше напряжённость, то есть напряжённость поля прямо пропорциональна количеству силовых линий, проходящих через площадку единичной площади, расположенную перпендикулярно линиям.
Потенциальность электростатического поля. Циркуляция поля вектора Е. Теорема о циркуляции вектора Е электростатического поля в инт. и диф. формах, их содержательный смысл.
Так как для напряженности электростатического поля справедлив принцип суперпозиции, то потенциальным является любое электростатическое поле.
Теорема о циркуляции вектора Е электростатического поля: Циркуляция Епо замкнутому контуру L всегда равно нулю.
В диф. форме:
Электростатическое поле является потенциальным.
Потенциальная энергия точечного заряда в электростатическом поле. Потенциал электростатического поля. Эквипотенциальные поверхности. Потенциал поля точечного неподвижного заряда. Принцип суперпозиции для потенциала.
Потенциальная энергия заряда в однородном электростатическом поле равна:
Потенциал –скалярная величина, является энергетической характеристикойполя в данной точке и равный отношению потенциальной энергии, которой обладает пробный заряд, к этому заряду.
Эквипотенциальная поверхность– это поверхность, на которой потенциал данного поля принимает одно и то же значение.
Потенциал поля точечного неподвижного заряда:
Принцип суперпозиций для потенциалов – Потенциал поля, созданного ГРУ ппой зарядов в произвольной точке равен сумме потенциалов полей, созданных каждым зарядом.
Момента
и приобретает потенциальную энергию
Диполь обладает:
· минимальной пот. энергией:
в положении (положение устойчивого равновесия);
· максимальной пот. энергией:
в положении (положение неустойчивого равновесия);
Во всех остальных случаях возникает момент сил, поворачивающий диполь в положение устойчивого равновесия.
Во внешнем неоднородной электростатическом поле на точечный диполь действует момент сил и этот диполь обладает потенциальной энергией
Сила, действующая на точечный диполь в неоднор. эл. стат. поле:
Во внешнем неоднородном эл. стат. поле точечный диполь под одновременным действием момента сил поворачивается в направлении поля и силы, перемещается в направлении, где по модулю больше (вытягивается в сторону более сильного поля).
В проводнике.
В проводнике имеются своб. заряды – носители тока, способные под действием сколь угодно малой силы перемещ. по всему объему проводника.
Электростатическая индукция – явление перераспределения зарядов на поверхности проводника под действием стор. электростатического поля.
Перераспредел. зарядов прекращ., когда любой точке проводника будет выполн. условие:
Т.к. , то напряженность электростатического поля в любой точке внутри проводника:
Поскольку то
– потенциал проводника одинак. во всех его внутр. точках и на поверхности
Условия стационарного распределения зарядов в проводнике:
1.Напряженность э-статического поля в любой точке внутри проводника равна нулю
2.Изб. заряды внутри проводника отсутств., а индуцированные заряды распределены
на его поверхности ( )
3.Вблизи внешней стороны поверхн. проводника вектор направлен по нормали к этой
поверхности в каждой её точке ( )
4.Весь объем проводника явл. эквипотенциальной обл., а его поверхность – эквипотенциальна
,
Контур с током в магнитном поле. Момент сил, действующих на контур с током, и потенциальная энергия контура с током в однородном магнитном поле. Работа сил магнитного поля при перемещении контура с током.
Магнитный момент линейного тока I, идущего по замкнутому плоскому контуру (все точки которого лежат в одной плоскости):
S – площадь поверхности, ограниченной контуром; в СИ [ ] = А*
Результирующая сила Ампера, действующая на контур с током в однородном магнитном поле равна 0.
Поэтому суммарный момент амперовых сил не зависит от выбора точки О, относительно которой он вычисляется:
Момент сил, действующий на замкнутый контур с током I в магнитном поле индукции :
При M=0 (т.е. контур с током находится в положении равновесия).
При на контур действует максимальный момент сил .
Потенциальная энергия замкнутого контура с током в магнитном поле:
Работа сил Ампера:
При этом направление положительной нормали образует правовинтовую систему. Данная формула справедлива в случае произвольного перемещения контура любой формы в магнитном поле.
29. Магнитное поле в веществе. Намагничение диа- и парамагнетиков. Вектор намагниченности . Теорема о циркуляции поля вектора в интегральной и дифференциальной форме.
Любое вещество – магнетик (т.е. способно намагничиваться под действием внешнего магнитного поля)
Ток проводимости (I, ) – ток, обусловленный направленным движением в веществе носителей тока.
Молекулярные токи ( ) – токи, связанные с орбитальным движением и спином элементарных частиц в атомах вещества. Каждый молекулярный ток обладает магнитным моментом.
Диамагнетики – вещества, магнитные моменты атомов которых в отсутствие внешнего магнитного поля равны нулю, т.е. магнитные моменты всех элементарных частиц атома (молекулы) скомпенсированы.
Парамагнетики – вещества, атомы которых в отсутствие внешнего магнитного поля имеют отличный от нуля магнитный момент, но их направление ориентировано хаотично, поэтому .
При внесении во внешнее магнитное поле диамагнетика в каждом его атоме индуцируется дополнительный момент , направленный против внешнего магнитного поля .
При внесении во внешнее магнитное поле парамагнетика магнитный момент его атомов (молекул) приобретают ориентированную по направлению внешнего поля .
Намагничение вещества обусловлено приемущественной ориентацией или индуцирование отдельных молекул в одном направлении. Намагничение вещества приводит к возникновению токов намагничения (усредненные по макроскопической области молекулярные токи):
где – вектор плотности тока намагничивания, идущего через ориентированную поверхность S.
Согласно принципу суперпозиции:
где – индукция внешнего поля;
– индукция магнитного поля токов намагничивания.
Вектор намагниченности – количественная характеристика намагниченного состояния вещества, равная отношению суммарного магнитного момента физически малого объема магнетика у этому объему :
В СИ [J] = А/м.
Теорема о циркуляции вектора магнитостатического поля в дифференциальной форме:
в любой точке магнитостатического поля ротор вектора равен вектору плотности тока намагничивания в этой же точке:
Теорема о циркуляции поля вектора в интегральной форме:
циркуляция вектора намагниченности магнитостатического поля по любому замкнутому конуру (L) равна алгебраической сумме токов намагничивания J’, охватываемых этим контуром:
30. Вектор напряженности магнитного поля. Теорема о циркуляции поля вектора в дифференциальной и интегральной форме. Магнитная восприимчивость и магнитная проницаемость вещества.
Величина:
– вектор напряженности магнитного поля.
Теорема о циркуляции вектора магнитостатического поля в дифференциальной форме:
Теорема о циркуляции поля вектора магнитостатического поля в интегральной форме:
Циркуляция вектора магнитостатического поля по любому контуру (L) равна алгебраической сумме токов проводимости, охватываемых этой поверхностью.
Для изотропных диамагнитных и парамагнитных сред :
где – магнитная восприимчивость, характерная для каждого магнетика:
где – магнитная проницаемость вещества.
31.Условия на границе раздела двух магнетиков для векторов . Закон преломления силовых линий.
Вблизи поверхности раздела двух изотропных магнетиков (при отсутствии токов проводимости) поля вектора удовлетворяют условиям:
на границе раздела 2-ух магнетиков:
1)нормальная составляющая вектора и тангенциальная составляющая вектора непрерывны;
2)тангенциальная составляющая вектора и нормальная составляющая вектора претерпевают разрыв.
Закон преломления силовых линий вектора (или ):
Электрический заряд и его основные свойства.
Источник
Силы электростатического взаимодействия зависят от формы и размеров наэлектризованных тел, а также от характера распределения заряда на этих телах. В некоторых случаях можно пренебречь формой и размерами заряженных тел и считать, что каждый заряд сосредоточен в одной точке.
Точечный заряд – это электрический заряд, когда размер тела, на котором этот заряд сосредоточен, намного меньше расстояния между заряженными телами. Приближённо точечные заряды можно получить на опыте, заряжая, например, достаточно маленькие шарики.
Взаимодействие двух покоящихся точечных зарядов определяет основной закон электростатики – закон Кулона. Этот закон экспериментально установил в 1785 году французский физик Шарль Огюстен Кулон (1736 – 1806). Формулировка закона Кулона следующая:
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональная произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.
Эта сила взаимодействия называется кулоновская сила, и формула закона Кулона будет следующая:
F = k · (|q1| · |q2|) / r2
где |q1|, |q2| – модули зарядов, r – расстояния между зарядами, k – коэффициент пропорциональности.
Коэффициент k в СИ принято записывать в форме:
k = 1 / (4πε0ε)
где ε0 = 8,85 * 10-12 Кл/Н*м2 – электрическая постоянная, ε – диэлектрическая проницаемость среды.
Для вакуума ε = 1, k = 9 * 109 Н*м/Кл2.
Сила взаимодействия неподвижных точечных зарядов в вакууме:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2]
Если два точечных заряда помещены в диэлектрик и расстояние от этих зарядов до границ диэлектрика значительно больше расстояния между зарядами, то сила взаимодействия между ними равна:
F = [1 /(4πε0)] · [(|q1| · |q2|) / r2] = k · (1 /π) · [(|q1| · |q2|) / r2]
Диэлектрическая проницаемость среды всегда больше единицы (π > 1), поэтому сила, с которой взаимодействуют заряды в диэлектрике, меньше силы взаимодействия их на том же расстоянии в вакууме.
Силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела (рис. 1.8).
Рис. 1.8. Силы взаимодействия двух неподвижных точечных заряженных тел.
Кулоновские силы, как и гравитационные силы, подчиняются третьему закону Ньютона:
F1,2 = -F2,1
Кулоновская сила является центральной силой. Как показывает опыт, одноимённые заряженные тела отталкиваются, разноимённо заряженные тела притягиваются.
Вектор силы F2,1, действующей со стороны второго заряда на первый, направлен в сторону второго заряда, если заряды разных знаков, и в противоположную, если заряды одного знака (рис. 1.9).
Рис. 1.9. Взаимодействие разноименных и одноименных электрических зарядов.
Электростатические силы отталкивания принято считать положительными, силы притяжения – отрицательными. Знаки сил взаимодействия соответствуют закону Кулона: произведение одноимённых зарядов является положительным числом, и сила отталкивания имеет положительный знак. Произведение разноимённых зарядов является отрицательным числом, что соответствует знаку силы притяжения.
В опытах Кулона измерялись силы взаимодействия заряженных шаров, для чего применялись крутильные весы (рис. 1.10). На тонкой серебряной нити подвешена лёгкая стеклянная палочка с, на одном конце которой закреплён металлический шарик а, а на другом противовес d. Верхний конец нити закреплён на вращающейся головке прибора е, угол поворота которой можно точно отсчитывать. Внутри прибора имеется такого же размера металлический шарик b, неподвижно закреплённый на крышке весов. Все части прибора помещены в стеклянный цилиндр, на поверхности которого нанесена шкала, позволяющая определить расстояние между шариками a и b при различных их положениях.
Рис. 1.10. Опыт Кулона (крутильные весы).
При сообщении шарикам одноимённых зарядов они отталкиваются друг от друга. При этом упругую нить закручивают на некоторый угол, чтобы удержать шарики на фиксированном расстоянии. По углу закручивания нити и определяют силу взаимодействия шариков в зависимости от расстояния между ними. Зависимость силы взаимодействия от величины зарядов можно установить так: сообщить каждому из шариков некоторый заряд, установить их на определённом расстоянии и измерить угол закручивания нити. Затем надо коснуться одного из шариков таким же по величине заряженным шариком, изменяя при этом его заряд, так как при соприкосновении равных по величине тел заряд распределяется между ними поровну. Для сохранения между шариками прежнего расстояния необходимо изменить угол закручивания нити, а следовательно, и определить новое значение силы взаимодействия при новом заряде.
Источник
Главная
Онлайн учебники
База репетиторов России
Тренажеры по физике
Подготовка к ЕГЭ 2017 онлайн
Глава 1. Электродинамика
Многие физические явления, наблюдаемые в природе и окружающей нас жизни, не могут быть объяснены только на основе законов механики, молекулярно-кинетической теории и термодинамики. В этих явлениях проявляются силы, действующие между телами на расстоянии, причем эти силы не зависят от масс взаимодействующих тел и, следовательно, не являются гравитационными. Эти силы называют электромагнитными силами.
О существовании электромагнитных сил знали еще древние греки. Но систематическое, количественное изучение физических явлений, в которых проявляется электромагнитное взаимодействие тел, началось только в конце XVIII века. Трудами многих ученых в XIX веке завершилось создание стройной науки, изучающей электрические и магнитные явления. Эта наука, которая является одним из важнейших разделов физики, получила название электродинамики.
Основными объектами изучения в электродинамике являются электрические и магнитные поля, создаваемые электрическими зарядами и токами.
Электрическое поле
1.1. Электрический заряд. Закон Кулона
Подобно понятию гравитационной массы тела в механике Ньютона, понятие заряда в электродинамике является первичным, основным понятием.
Электрический заряд – это физическая величина, характеризующая свойство частиц или тел вступать в электромагнитные силовые взаимодействия.
Электрический заряд обычно обозначается буквами q или Q.
Совокупность всех известных экспериментальных фактов позволяет сделать следующие выводы:
Существует два рода электрических зарядов, условно названных положительными и отрицательными.
Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический
заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.Одноименные заряды отталкиваются, разноименные – притягиваются. В этом также проявляется принципиальное отличие электромагнитных сил от гравитационных. Гравитационные силы всегда являются силами притяжения.
Одним из фундаментальных законов природы является экспериментально установленный закон сохранения электрического заряда.
В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака.
С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному заряду e.
В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион.
Заряд может передаваться от одного тела к другому только порциями, содержащими целое число элементарных зарядов. Таким образом, электрический заряд тела – дискретная величина:
Физические величины, которые могут принимать только дискретный ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда. Следует отметить, что в современной физике элементарных частиц предполагается существование так называемых кварков – частиц с дробным зарядом
и Однако, в свободном состоянии кварки до сих пор наблюдать не удалось.
В обычных лабораторных опытах для обнаружения и измерения электрических зарядов используется электрометр – прибор, состоящий из металлического стержня и стрелки, которая может вращаться вокруг горизонтальной оси (рис. 1.1.1). Стержень со стрелкой изолирован от металлического корпуса. При соприкосновении заряженного тела со стержнем электрометра, электрические заряды одного знака распределяются по стержню и стрелке. Силы электрического отталкивания вызывают поворот стрелки на некоторый угол, по которому можно судить о заряде, переданном стержню электрометра.
| Рисунок 1.1.1. Перенос заряда с заряженного тела на электрометр |
Электрометр является достаточно грубым прибором; он не позволяет исследовать силы взаимодействия зарядов. Впервые закон взаимодействия неподвижных зарядов был открыт французским физиком Ш. Кулоном в 1785 г. В своих опытах Кулон измерял силы притяжения и отталкивания заряженных шариков с помощью сконструированного им прибора – крутильных весов (рис. 1.1.2), отличавшихся чрезвычайно высокой чувствительностью. Так, например, коромысло весов поворачивалось на 1° под действием силы порядка 10–9 Н.
Идея измерений основывалась на блестящей догадке Кулона о том, что если заряженный шарик привести в контакт с точно таким же незаряженным, то заряд первого разделится между ними поровну. Таким образом, был указан способ изменять заряд шарика в два, три и т. д. раз. В опытах Кулона измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие заряженные тела принято называть точечными зарядами.
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь.
| Рисунок 1.1.2. Прибор Кулона |
| Рисунок 1.1.3. Силы взаимодействия одноименных и разноименных зарядов |
На основании многочисленных опытов Кулон установил следующий закон:
Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
Силы взаимодействия подчиняются третьему закону Ньютона: Они являются силами отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках (рис. 1.1.3). Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.
Закон Кулона справедлив для точечных заряженных тел. Практически закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними.
Коэффициент пропорциональности k в законе Кулона зависит от выбора системы единиц. В Международной системе СИ за единицу заряда принят кулон (Кл).
Кулон – это заряд, проходящий за 1 с через поперечное сечение проводника при силе тока 1 А. Единица силы тока (ампер) в СИ является наряду с единицами длины, времени и массы основной единицей измерения.
Коэффициент k в системе СИ обычно записывают в виде:
где
– электрическая постоянная.
В системе СИ элементарный заряд e равен:
e = 1,602177·10–19 Кл ≈ 1,6·10–19 Кл.
Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции.
Если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.
Рис. 1.1.4 поясняет принцип суперпозиции на примере электростатического взаимодействия трех заряженных тел.
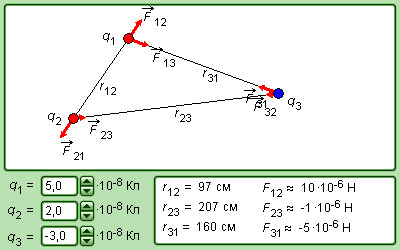 |
Модель. |
Принцип суперпозиции является фундаментальным законом природы. Однако, его применение требует определенной осторожности, в том случае, когда речь идет о взаимодействии заряженных тел конечных размеров (например, двух проводящих заряженных шаров 1 и 2). Если к системе из двух заряженных шаров поднсти третий заряженный шар, то взаимодействие между 1 и 2 изменится из-за перераспределения зарядов.
Принцип суперпозиции утверждает, что при заданном (фиксированном) распределении зарядов на всех телах силы электростатического взаимодействия между любыми двумя телами не зависят от наличия других заряженных тел.
Источник
